1.Introduction
Many contemporary problems in atomic, nuclear, solid state, rotational and vibrational spectroscopy involve obtaining the exact or approximate solutions of the relativistic and non-relativistic wave equation describing the dynamics of the quantum system under consideration. This is so because the wavefunction contains all the necessary information needed to describe the behaviour of the system. Recently, many authors have obtained both the exact (ℓ = 0) and approximate (ℓ ≠ 0) solutions of some exponential type potentials which include inverted generalized hyperbolic potential 1, Hulthen potential 2-4, Rosen-Morse potential5 Poschl-Teller potential 6,7, Eckart potential 8, modified Hylleraas potential 9, generalized Morse potential 10, Woods-Saxon potential 11, Manning-Rosen potential 12,13 among others. This was achieved by employing appropriate approximation schemes Pekeris 14, Greene and Aldrich 15 and even more recently improved ones 2,16-18 to accommodate large values of the screening parameters.
Some of the techniques devised to investigate these potentials are. Asymptotic Iteration Method (AIM) 5,13,19, Nikiforov-Uvarov (NU) method 20,21, shape invariant supersymmetry (SUSYQM) 22, Modified factorization method (MFM) 23, Formula method 24, Exact quantization rule 25-27, Factorization method 28 and others.
The Klein-Gordon equation containing a four vector linear momentum operator and a rest mass requires introducing the four vector potential V(r) and a space time scalar potential S(r). With the configuration S(r)=V(r) or S(r)= −V(r), it has been shown extensively in literature that the Klein-Gordon equation and Dirac Equation share the same energy spectrum 29. While for S(r)=V(r)=2V(r), gives non-relativistic limits of the equation conforming exactly to that of the Schrödinger equation 30-32.
The Hellmann potential 33-36 is a short range potential. It is a combination of Yukawa and Coulomb potentials. This potential have been investigated extensively by various authors. For instance, 36 used the shape invariant supersymmetric approach to solve analytically the three-dimensional Schrödinger equation with this potential by applying the well-known Greene and Aldrich approximation 37 scheme to deal with the centrifugal barrier 38 obtained approximate eigensolutions of the Duffin-Kemmer-Petiau and Klein-Gordon equations with Hellmann potential 39 solved the Schrödinger equation with Hellmann potential using the parametric Nikiforov-Uvarov method. This potential finds more application in the field of atomic and condensed matter physics, electron-core 40,41, electron-ion 42 inner-shell ionization problem, alkali hydride molecules and solid state physics 43,44.
In addition, the Deng-Fan Oscillator Potential 45,46 is applied in molecular physics, atomic physics, and quantum chemistry. It is used to describe the interactions of molecular structure in quantum mechanics for diatomic molecules. This potential is the generalized Morse potential 47,48. It has physical boundary conditions at r= 0 and ∞. It has the correct asymptotic behaviour as the inter-nuclear distance approaches zero 47,48. It has been used it has been used extensively to describe diatomic molecular energy spectra and electromagnetic transitions 49. The bound state solutions of the relativistic and non-relativistic wave equations have been studied by several authors with this potential 27,50-52.
Also, the authors of Ref.53 proposed the Hellmann-generalized Morse potential model and solved the Schrödinger equation with it. Motivated by the success of these investigation, we attempt to solve the Klein-Gordon and Dirac equations with this potential following the Nikiforov-Uvarov method. We’ll also apply the non-relativistic energy equation obtained to study some selected diatomic molecules with the aid of some spectroscopic parameters. The potential is of the form 53;
The work is organised as follows; in the next section, we review the NU method. The eigensolutions of Klein-Gordon and Dirac equation with the Hellmann- generalized Morse potential and their non-relativistic limits conforming to the spectrum of the Schrödinger equation are obtained in Sec. 3, while Sec. 4 presents the numerical results with plots for the energy spectrum . Finally, we give our concluding remarks of the findings in Sec. 5.
2.Review of Nikiforov-Uvarov Method
The Nikiforov-Uvarov (NU) method is based on solving the hypergeometric-type second-order differential equations by means of the special orthogonal functions. The main equation which is closely associated with the method is given in the following form
Where σ(s) an
This transformation reduces Eq. (2) into a hypergeome- tric-type equation of the form
The function ϕ(s) can be defined as the logarithm derivative
where
with π(s) being at most a first-degree polynomial. The second ψ(s) being χ n (s) in Eq. (3), is the hypergeometric function with its polynomial solution given by Rodrigue’ relation
Here, B n is the normalization constant and ρ(s) is the weight function which must satisfy the condition
It should be noted that the derivative of τ(s) with respect to s should be negative. The eigenfunctions and eigenvalues can be obtained using the definition of the following function π(s) and parameter λ, respectively:
where
The value of k can be obtained by setting the discriminant of the square root in Eq. (9) equal to zero. As such, the new eigenvalue equation can be given as
3.Approximate Solutions of the Hellmann-generalized Morse potential
3.1.Bound state solution of the Klein-Gordon equation
The Klein-Gordon equation for a spinless particle for ℏ =c= 1 in D-dimensions is given as 62
Where ∇2 is the Laplacian, M is the reduced mass, E nl is the energy spectrum, n and l are the principal and angular momentum quantum numbers, respectively (or vibration-rotation quantum number in quantum chemistry). It is a common practise that for the wavefunction to satisfy the boundary conditions it can be rewritten as ψ(r,θ,φ)=(R nl /r)Y lm (θ,φ). However, the spherical harmonics Y lm (θ,φ) are already known in literature 54 and the angular component of the wavefunction could be separated leaving only the radial part.
So the radial part of the equation becomes
Thus, for equal vector and scalar potentials V(r)=S(r)=2V(r) Eq. (14), becomes
The Greene and Aldrich approximation scheme 37 for the centrifugal term of the Klein-Gordon equation is given as
Using Eq. (1) with q=e αr e − 1, then, Eq. (14) becomes
using s=e −αr , so as to enable us to apply the NU method and substituting Eq. (15) into (16), we have
Eq. (17) can be simplified further by using the following dimensionless ansatz:
Substituting the ansatz and simplifying, we obtain
Comparing Eq. (19) with Eq. (2), we obtain the following polynomials;
Substituting these polynomials into Eq. (9), we get π(s) to be
To find the value for k, the discriminant of the expression in the square root in Eq. (21) must vanish. So we obtain
Substituting k of Eq. (22) into Eq. (21) yields
From Eq. (8), the condition for the bound state solution of the NU equation is satisfied; thus
However, the parameter is obtained from Eq. (10) to be
And employing Eq. (11), we obtain
The condition for obtaining the bound state energy eigenvalue equation requires that λ=λ n , so equating this, and simplifying yields
where upon substituting the ansatz of Eq. (18) into (27) gives the energy eigenvlaue equation
with
3.2.Non-relativistic limit
In this section, we consider the non-relativistic limit of Eq. (28). Considering a transformation of the form: M+E nl → 2μ/ℏ2 and M−E nl → −E nl and substitute it into Eq. (28), we have the non-relativistic energy equation as
To obtain the corresponding wavefunction, we consider Eq. (5), and upon substituting Eq. (18) and (20) and integrating, we get
To get the hypergeometric function considering Eq. (3), we first calculate the weight function following Eq. (7) as
Then, from the Rodrigues’ equation, Eq. (6), the hypergeometric equation here is expressed in Jacobi polynomial as
So that the wavefunction is
From the definition of Jacobi polynomials 37,
So, Eq. (34) is rewritten in terms of hypergeometric polynomial as
Where
From the normalization condition, we have that
And in our coordinate transformation as s=e −αr , we have that
Now, letting y= 1 − 2s, we obtain
According to Onate et al, 38, an integral of the form Eq. (40) can be expressed as
Therefore, comparing Eq. (40) and (41), we obtain the normalization constant as
3.3.Fermionic massive spin 1/2 particles interacting with Hellmann-generalized Morse potential model
In this section, we briefly review the Dirac equation. The Dirac equation with scalar S(r) and V(r) potentials in spherical coordinates is given as 55
where E denotes the relativistic energy of the system,
where I is the 2 × 2 unitary matrix and
For a particle in a spherical field, the total angular momentum operator j and the spin-orbit matrix operator k= (σ⋅L+1), where σ and L are the Pauli matrix and orbital angular momentum, respectively, commute with the Dirac Hamiltonian. The eigenvalues of k are k= −(j+ 1/2) for the aligned spin (s 1/2 ,p 3/2 ,etc) and k= (j+1/2) for the unaligned spin (p 1/2 ,d 3/2 ,etc). The complete set of conservative quantities can be chosen as (H,K,J 2 ,J z ). The Dirac spinor is
where
which translate to:
for k(k+ 1)=ℓ(ℓ+1),r∈ (0, ∞),
for , r∈ (0, ∞) where Δ(r)=V(r)−S(r) and Σ(r)=V(r)−S(r) are the difference and the sum potentials, respectively.
3.4.Spin symmetry solutions of the Dirac equation with Hellmann-generalized Morse potential model
Under this symmetry, d[V(r)−S(r)]/dr=dΔ(r)/dr= 0, Δ(r)=C s = constant, then the spin symmetry is exact in the Dirac equation. In this symmetry limit, we take Σ(r) as the potential in the following form:
Substituting Eq. (51) into Eq. (49), we have; m
To obtain the solution for k≠ 0, we use Eq. (15) 37 to deal with the centrifugal term, and transforming as s=e −αr so as to make Eq. (52) conform to Eq. (2) satisfying the upper-spinor component F n,k (s) then, we have
where
Comparing Eq. (53) and Eq. (2), as usual yields the following parameters
Substituting these polynomials into Eq. (9), we get π(s) to be
Also, to find the constant, the discriminant of the expression under the square root of Eq. (57) should be equal to zero. As such, we have that
Substituting Eq. (58) into Eq. (58) yields
Taking the derivative of π(s) in Eq. (59) with respect to s yields
From the knowledge of NU method, we choose the expression π(s)_ which the function τ(s) has a negative derivative. This is given by
with τ(s) being obtained as
Referring to Eq. (10), we define the constant λ as
Taking the derivative of Eq. (62) with respect to s, we have;
From Eq. (11), we obtain;
By comparing Eqs. (63) and (65), the exact energy eigenvalue equation is obtained as
The corresponding wave functions can be evaluated by substituting π_(s) and σ(s) from Eq. (59) and Eq. (56) respectively into Eq. (5) and solving the first order differential equation, this gives the corresponding upper-spinor component as;
From the definition of the Jacobi Polynomials 20,
In terms of hypergeometric polynomials, Eq. (69) can be written as
where (2ω+1) n is the Pochhammer’s symbol (for the rising factorial).
Using the normalization condition, we obtain the normalization constant as follows:
Substituting Eq. (69) into Eq. (75), we have
where
Comparing Eq. (76) with the integral of the form
We have the normalization constant as
3.5.Pseudospin symmetry solutions of the Dirac equation with the Hellmann-generalized Morse potential model
In the pseudospin symmetry limit, d∑(r)/dr= 0 and ∑(r)=C ps = constant. Thus, our potential is taken as
substituting Eqs. (81) into Eq. (50), we obtain
Under this limit, similarly, we define s=e −αr , then, Eq. (82) becomes
Where
Using the same procedure as in spin symmetry above, we obtained the negative energy of the pseudospin symmetry as
The lower-spinor component of the wave function is obtained following the same procedure as;
From the definition of the Jacobi Polynomials 20,
In terms of hypergeometric polynomials, Eq. (86) can be written as
where (2Ω +1) n is the Pochhammer’s symbol (for the rising factorial).
3.6.Non-relativistic limit
In this section, we obtained the non-relativistic limit of the spin symmetry limit. The non-relativistic
Schrödinger equation is bosonic in nature, i.e. spin does not involve in it. On the other hand, relativistic Dirac equation is for a spin 1/2 particle. This immediately suggests that there may be a certain relation between the solutions of the two fundamental equations 56-58. The meaning is that, the non-relativistic energies E nl can be determined by taking the non-relativistic limit values of the relativistic eigenenergies E. Therefore, taking C s = 0 and using the transformations M+E nk → (2μ/ℏ2) and M−E nk →E n, ℓ together with k→ ℓ 56-57, the relativistic energy Eq. (68) reduces to
We have the normalization constant as
4.Numerical results and discussion
By using the well-known spectroscopic values in Table I, we computed the energy eigenvalues of the Hellmann-generalized Morse Potential for some selected diatomic molecules (for N2, CO, NO, CH and HCl) using the non-relativistic energy equation for various vibrational n and rotational ℓ quantum number, as shown in Table II. In Fig. 1, we plot the shape of the potential. This shows explicitly the behaviour of the potential under consideration. In Fig. 2, we show the variation of the energy spectrum with various values of the rotational and vibrational quantum numbers. It is seen that for fixed value of ℓ, the energy eigenvalues increases as n increases. There’s also a spread at n= 0 but a uniform convergence as n→ 10. In Figs. 3 and 4, we show the variation of the energy eigenvalues with dissociation energy (in cm−1) and equillibrium bond length r (in Å) respectively for various vibrational quantum number. The energy increases monotonically in both cases. We observe in Fig. 5 that as the adjustable screening parameter increase, the energy eigenvalue increases in a quasi-linear manner. There is a uniform decrease in the energy eigenvalues as the parameter “a” increases, this is shown in Fig. 6. The energy eigenvalue increases as the parameter “b” increases up to b= 3, beyond this point, the energy decreases.
Table 1 The potential model parameters for some diatomic molecules 59
| Molecules | De(cm-1) | re(Å) | μ(amu) |
| CH | 31838.08 | 1.1198 | 0.929931 |
| NO | 64877.06 | 1.1508 | 7.468441 |
| CO | 87471.43 | 1.1282 | 6.860586 |
| N2 | 96288.04 | 1.0940 | 7.003350 |
| HCl | 37,255.00 | 1.2746 | 0.980105 |
Table II Energy eigenvalues (in eV) in 3D for various vibrational quantum number and α =0.025 for CH, NO, CO N2, HCl with ћc=1973.29 eV Å
| N | 1 | CH | NO | CO | N2 | HCl |
| 0 | 0 | -2.669578479 | -2.208833696 | -2.057168210 | -2.090263840 | -2.146705710 |
| 1 | 0 1 |
-2.397864979 -2.392210914 |
-2.103866806 -2.103326846 |
-1.935855630 -1.935282930 |
-1.961918940 -1.961329540 |
-1.924396284 -1.920701408 |
| 2 | 0 1 2 |
-2.142262376 -2.136937738 -2.126315533 |
-2.000467316 -1.999935346 -1.998871537 |
-1.816205960 -1.815641030 -1.814511320 |
-1.835286920 -1.834705280 -1.833542130 |
-1.712628335 -1.709105695 -1.702071683 |
| 3 | 0 1 2 3 |
-1.901521961 -1.896501566 -1.886485915 -1.871524996 |
-1.898604212 -1.898080047 -1.897031875 -1.895460006 |
-1.698188930 -1.697631630 -1.696517160 -1.694845800 |
-1.710337410 -1.709763420 -1.708615560 -1.706894110 |
-1.510745969 -1.507384983 -1.500673639 -1.490633087 |
| 4 | 0 1 2 3 4 |
-1.674513710 -1.669774726 -1.660320149 -1.646196510 -1.627472860 |
-1.798247185 -1.797730694 -1.796697836 -1.795148948 -1.793084493 |
-1.581774980 -1.581225160 -1.580125670 -1.578476760 -1.576278860 |
-1.587040750 -1.586474270 -1.585341430 -1.583642500 -1.581377920 |
-1.318143535 -1.314934415 -1.308526216 -1.298938890 -1.286202222 |
| 5 | 0 1 2 3 4 5 |
-1.460212987 -1.455734691 -1.446799912 -1.433452000 -1.415755311 -1.393794428 |
-1.699366720 -1.698857735 -1.697839905 -1.696313552 -1.694279120 -1.691737223 |
-1.466935230 -1.466392760 -1.465307970 -1.463681110 -1.461512590 -1.458803000 |
-1.465367930 -1.464808840 -1.463690750 -1.462013950 -1.459778880 -1.456986010 |
-1.134261051 -1.131194757 -1.125071629 -1.115910550 -1.103739628 -1.088596024 |
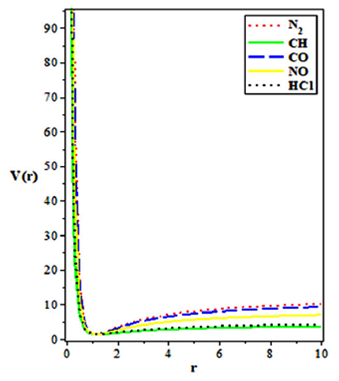
FIGURE 1 The shape of Hellmann-generalized Morse potential (r in Å ) for the slected diatomic molecules.
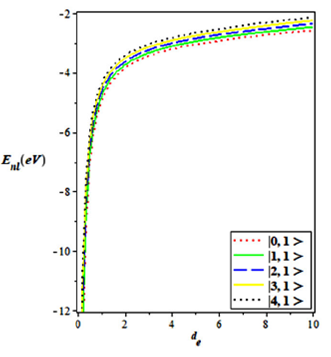
FIGURE 3 Energy eigenvalues variation with dissociation energy (in cm-1) for various vibrational quantum number.
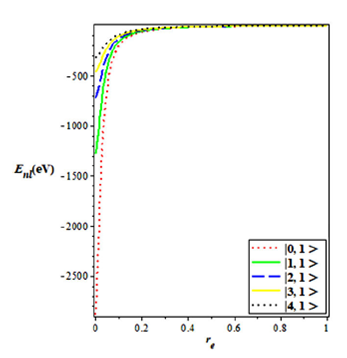
FIGURE 4 Energy eigenvalues variation with equillibrium bond length r (in Å ) for various vibrational quantum number.
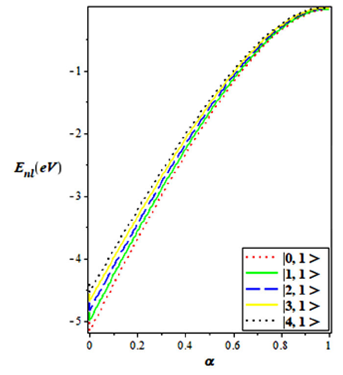
FIGURE 5 Energy eigenvalues variation with adjustable screening parmeter for various vibrational quantum numbers.
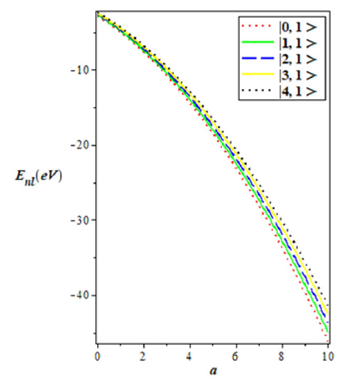
FIGURE 6 Energy eigenvalues variation with potential strength for various vibrational quantum numbers.
5.Conclusion
In this paper, approximate bound-state solutions of the Schrödinger, Klein-Gordon and Dirac equations for the Hellmann-generalized Morse model potential was considered. For each wave equation, and by applying an appropriate approximation to the centrifugal term, we have obtained the energy eigenvalues and the corresponding wave functions for any quantum state. To show the accuracy of our findings, we compute the numerical energy spectra for some diatomic molecules using some spectroscopic parameters and figures that discuss the energy spectrum in each case. It is interesting to note here that the results obtained from this consideration finds application in various branches of physics and chemistry where non-relativistic and relativistic phenomena are studied.











 nueva página del texto (beta)
nueva página del texto (beta)




