1. Introduction
The search for exact solutions of nonlinear systems has reached an unprecedented speed these days. The best known solitons solutions have found their applications in various fields just to name a few such as optical fibers, plasm, biology, quantum physics . Thus, solitons did not remain anonymous for a long time because of their direct implications in trans-continental and trans-oceanic data transport [1-24]. Without doubt, soliton is the one important wave which marveled in the field of data transport and securing it. It should also be noted that the most moving side of solitary waves comes from the fact that they are associated with chirped pulses. These chirped pulses, have been widely investigated in diverse shape in recent years by [27-29].
From this, many results in theoretical and experimentally have been followed with the mathematical tools to handle them [10, 35, 36]. These analytical methods facilitated the success of these results are among others, the Sine-Gordon expansion method, the modified exp(−ψ(ξ))expansion function method,(G’/G)-expansion scheme, the trial expansion method, the new mapping method, the auxiliary equation method, the rational function method, and the Riccati-Bernoulli sub-ODE method [25-30,35-45]. In this present work, an investigation will be carried out in order to formulate new shape of the chirped soliton solutions to the famous (2+1)-dimensional complex GinzburgLandau equation (GLE), of which skeletal structure is as follows [29-33]:
ψ(x,t) represents complex wave profile on (2+1)dimensional space time R 2+1, while t represents the temporal variable and x,y represent spatial variable. α, λ, γ and G are real. The set of the CGLE Eq. (1) was recently used to depict the beginning of stationary periodic solutions in nonlinear stability problems. It takes the name of real Ginzburg-Landau equation when (α = λ = 0) [30]. To get right to the purpose, the work is organized as follows: Section 2 is devoted to the traveling-wave solution. Section 3 is used the linear stability technic to study the modulation instability gain spectrum. Section 4 will depicts the obtained analytical results with their physical explanation. The last part of the work will present the conclusions of this work.
1.1. Analytical investigation and traveling waves solution
The following envelope transformation is used to build soliton solution
where ϕ(ζ) is real function and the chirp component is A(ζ)), with ξ and ζ given by ξ = kx + ly + vt + ξ 0 and ζ = nx + my + ωt + η 0, respectively. Inserting Eq. (2) into Eq. (1) splits imaginary and real parts as
and
Suppose that the chirp is given by
where A 0 is an arbitrary constant to obtain later. Plugging Eq. (5) into Eq. (4) and Eq. (3), we get
and
where
To deal with an analytical solutions to Eq. (7) and Eq. (6), we suppose that
Then Eq. (7) and Eq. (6) become
It has become easy to investigate soliton-like solutions now. For this purpose, we considered the following expression as solution [45]
and n an arbitrary constant, while F(ξ) is taken like solutions of the following ordinary differential equation [45]
With the homogeneous balance principle between ϕϕ’’ and ϕ 4, it is obtained n+n+2p = 4n ⇒ p = n. From which Eq. (11) turns to
Using the set of equations given by Eq. (13) together with Eq. (12) and make use of into Eq. (10) or Eq. (9) gives the set of system of equation in terms of F jp (ζ)(j = 2,3,4,5,6,8)
Thereafter solving the obtained set of system of Eq. (14) by using the mathematical software Maple 18, it is revealed.
We can thus unroll the types of solutions of Eq. (1), as well as the corresponding chirped solutions
Case 1: If A = 0, B = 0,D = 0, it is recovered bright soliton of Eq. (1):
and the bright chirp is
a periodic function solutions
and the periodic chirp
then a rational solution
and the rational chirp
Case 2: By setting the variables A = 0, B = 0, we deduce three forms of solutions of Eq. (5):
and the chirp
it is gained for C > 0, E > 0,
the corresponding chirp gives
and
with the chirp
Case 3: Considering A = B = 0, C > 0, we have gained combined bright soliton and hyperbolic functions solutions of Eq. (5):
the corresponding chirp
with the corresponding chirp
For D 2-4CE >0, ε=±1
the chirp gives
for D 2 − 4CE < 0, ε = ±1
the chirp is
the chirp is given by
for D 2 − 4CE = 0, ε = ±1
the corresponding chirp
for E > 0, ε = ±1
the chirp is revealed as
for E > 0, ε = ±1
and the corresponding chirp
the chirp gives
and the corresponding chirp as
Case 4: Considering A = B = 0, C < 0, we have gained combined bright soliton and hyperbolic functions as solutions For D 2 − 4CE > 0
the chirp gives
for D 2 − 4CE > 0,
the chirp gives
for D 2 − 4CE > 0, ε = ±1,
the chirp reads as follows
for D 2 − 4CE > 0, ε = ±1,
the chirp is given by
for E > 0, ε = ±1,
the chirp is obtained
for D 2 − 4CE > 0, E > 0, ε = ±1,
the chirp is
Case 5: For A = B = 0, C > 0,ε = ±1,
the chirp component is
the chirp gives
The last chirp gives
1.2. Modulation analysis
This section will be using linear analysis technique to take out the modulation instability (MI) gain spectrum. Assuming the steady state solution of Eq. (1) in the form of:
where P 0 is the incident power. B(x,y,t) is the small perturbation component and B ∗(x,y,t) is the complex conjugate. Inserting Eq. (66) into Eq. (1) lead to
Suppose the solution of Eq. (67) is in the following expression
where a j (j = 1,2) are reals, and K and Ω are wave numbers and the modulation frequency, respectively. The quantity Γ is the transverse wave number of the perturbation. Inserting Eq. (68) into Eq. (67) gives the set of linear of coupled equations for α1 and α2
This set of coupled of equation has a nontrivial solution when the determinant of the matrix below vanishes
Thereafter, the MI gain spectrum is revealed as
Now to investigate the behavior of Eq. (71), we first point out the condition of the obtaining the steady state. So, it is important to highlight the fact that the perturbation grow exponentially, when the wave number value contains the imaginary part, in this condition the steady state solution is unstable. However, in case of small perturbation and having the wave number with real value, the steady state of the solution is stable.
Here two cases are going to be discussed:
• Case 1: In this case, the steady state is stable again and a small perturbution is seen if K is real
but if λ, γ and G are non zero value, the inequality Eq. (72) is invalid. Consequently the steady is still unstable.
• Case 2: In this case, the MI occurs when K is imaginary due to the fact that the perturbation increases exponentially and in the same time
in the same way if (λ, γ , G ≠ 0) it remains invalid. To analyze the MI gain spectrum, we suppose that λ = γ = G = 0. Consequently the increase rate of MI gain spectrum G(K) = 2Im(K) is given by
1.3. Physical explanation and Modulation instability analysis
Figure 1 is the illustration of the MI gain spectrum versus wave number with the effect of incident power. It is observed that when the incident power increase the unstable band also increase. So, at the maximum incident power, it remains stable (see Fig. 1d). Meanwhile, Fig. 2 is illustration of the MI gain spectrum with small value of the incident power. The unstable plage increase when the incident power value is to small (see black line). Futhermore, Fig. 3 is the illustration of the MI gain spectra versus wave number under the effect of the transverse wave number. For Γ = 70.50, one side lobe is obtained and 38 ≤ K ≤ 100. Figures 4a) and b) have depicted the chirped bright 3D and 2D for values of n=0.5, m=0.14, α = 0.02, G = 2.7, l = −0.3, γ = 0.12, y = 0.5, E = −0.5, C = 0.1106, ω = 0.15. Moreover, Figs. 5a), b), c) and d) are chirp kink-like soliton obtained for the values of A 0 = −7.5,n = 0.5,m = 0.14,α = 0.2,G = 1.7,l = −1.3,γ = 0.12,x = 0,E = 1.5,C = 0.3820.
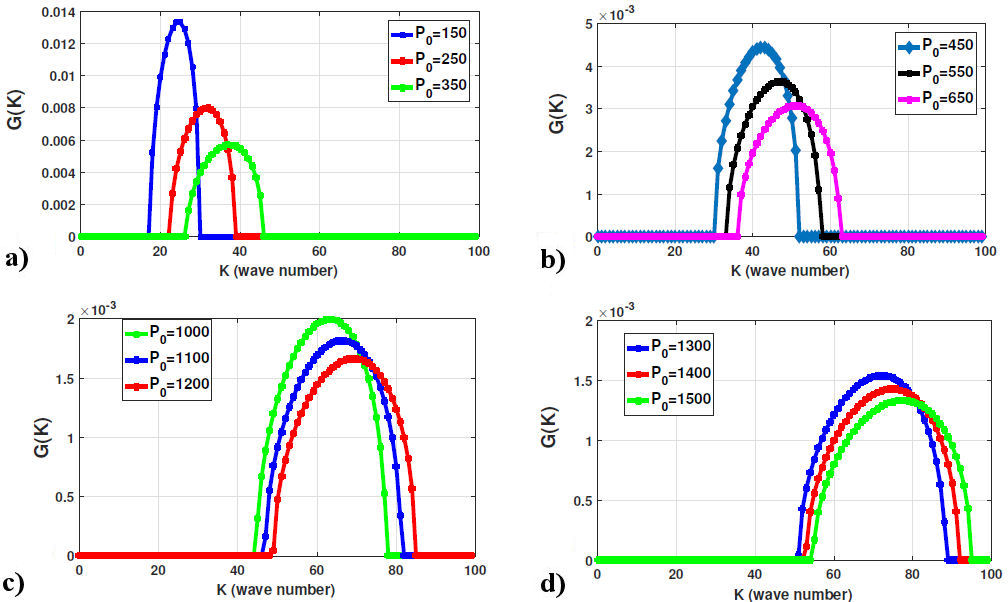
FIGURE 1 (Color online) Variation of MI gain spectrum versus wave number with the effect of the incident power a) [P 0 = 150, P 0 = 250, P 0 = 350], b) [P 0 = 450, P 0 = 550, P 0 = 650], c) [P 0 = 1000, P 0 = 1100, P 0 = 1200], d) [P 0 = 1300, P 0 = 1400, P 0 = 1500] at α = 0.1,Γ = 0.5.
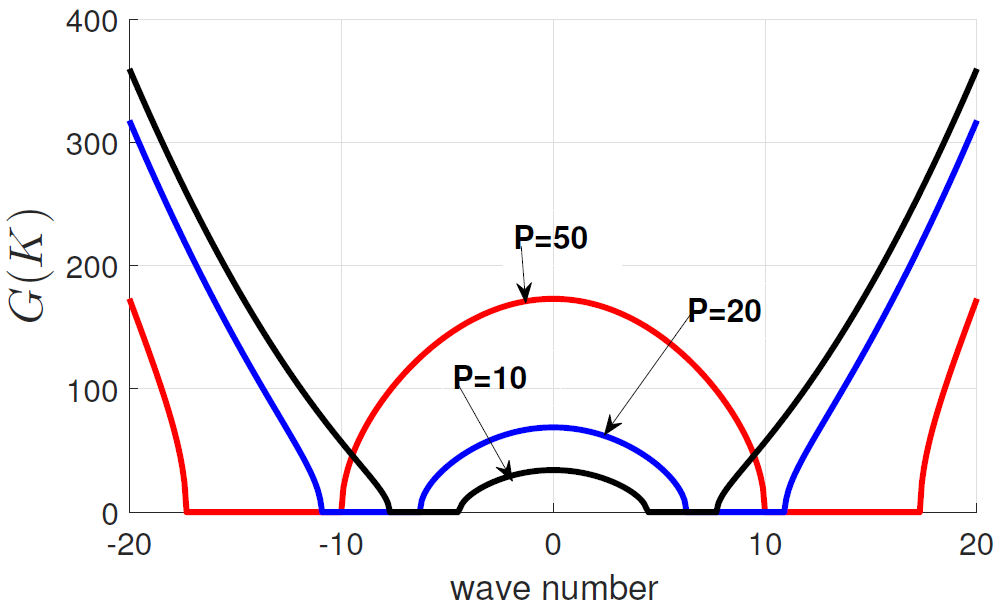
FIGURE 2 Plot of the MI gain spectrum versus wave number with the effect of the incident power (black line [P 0 = 10], blue line [P = 50] and red line [P = 20]) at α = 0.75,Γ = 0.75.
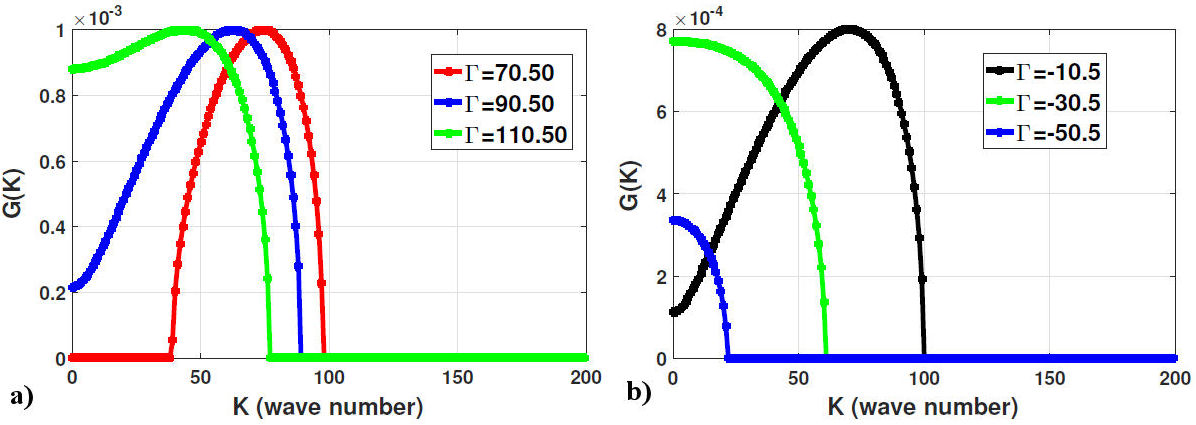
FIGURE 3 (Color online) variation of the MI gain spectra versus wave number with the effect of the transverse wave number a) [Γ = 70.50, Γ = 90.50, Γ = 110.50] and b) [Γ = −10.50, Γ = −30.50, Γ = −50.50] at α = 0.05, P 0 = 2500 respectively.
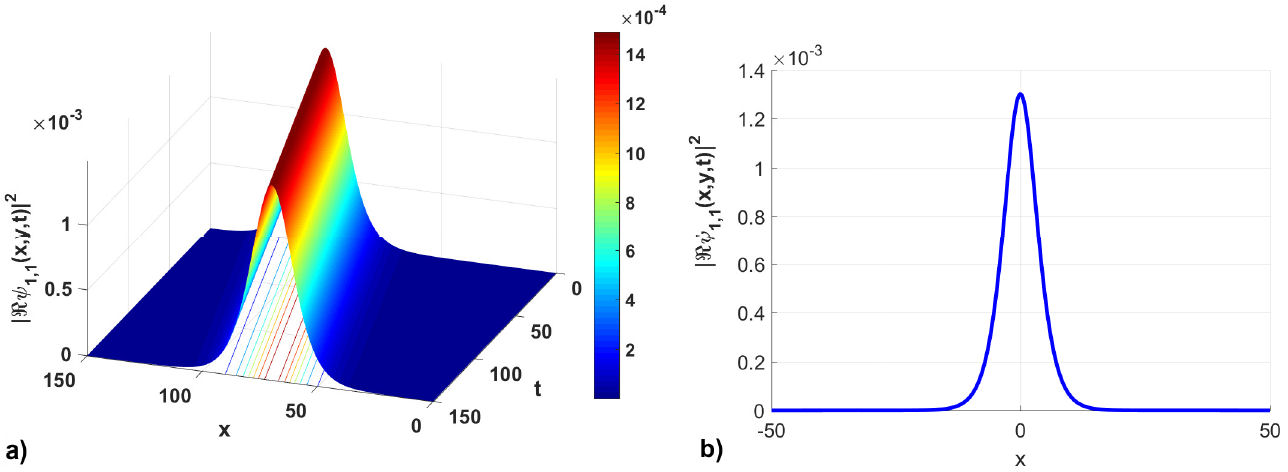
FIGURE 4 Spatiotemporal plot evolution a) 3-D (left panel) and b) 2-D
(right panel) of the chirp bright of
2. Conclusion
This work addresses new shape of the chirped bright and dark soliton solutions through the CGLE by using the new sub-ODE equations. By using a special ansatz of the traveling wave transformation, we obtain a new shape of the chirp comparatively to the previous works reported in literature [26,31-34,36,45]. In addition, new singular soliton solutions, trigonometric function solutions and complex traveling waves have been obtained. The obtained results are new in the field of solitons. The authors hope that these results will be very useful to explain physical phenomenons in diverse field of science and engineering. In addition, the different parameters of the CGLE have play an important role during graphical representation of the analytical results. Finally, the linear analysis technique has been applied to the investigation the steady state of the MI gain spectrum and also to point out the different regime of instability.











 nueva página del texto (beta)
nueva página del texto (beta)



