1 Introduction

The theory of scattering of a monochromatic electromagnetic plane wave from a sphere goes back to the first decade of the 20th century [¹] . Subsequently, A. L. Aden and M. Kerker [²] found the first analytical solution for the scattering of an electromagnetic wave from a core/shell particle with spherical symmetry. Y. Nomura and K. Takuka obtained the rigorous solution of Maxwell’s equations in an inhomogeneous medium, which led to description of the electromagnetic waves propagation across the atmosphere, it is treated like many layers of concentric spheres [³]. C. T. Tai presented a general discussion of the electromagnetic field involved in a radially stratified medium [⁴]. Generalization of the problem of the scattering of an electromagnetic wave from a spherical core/shell particle was done for any number of concentric homogeneous regions [⁵].

One of the first computational studies to analyze the optical properties of core/shell particles was made by R. W. Fenn and H. Oser [⁶]. The first quantitative study comparing numerical and experimental results of scattered light by dielectric spheres coated by a spherical shell of a second material (silver chloride-core/linolenic acid (C₁₈H₃₂O₂)-shell), was performed by W. F. Espenscheid et al. [⁷]. A summary of the scattering theory and some practical applications was developed by M. Kerker [⁸]. However, computational errors were found to evaluate the Bessel functions [^7,8,9,10], which appear in the work developed by M. Kerker et al. [¹¹]. The code advance solved those errors and the numerical study of the interaction between core/shell particles with electromagnetic waves has been more accurate [^12,13,14,15]. Currently, BHCOAT [¹²] is one the most used algorithms to calculate the absorption, extinction and scattering cross section of a core/shell particle. Since then, different researches have been studying, with this code, the interaction between an electromagnetic wave and core/shell particles, especially those which the core is a dielectric and shell is a metal (also named as nanoshell [¹⁶]) [^17,18,19]. e.g., N. Harris et al. demonstrated that the geometry of gold nanoshells causes a maximum surface heat flux [¹⁷].

One of the highly analyzed aspects is the excitation of localized surface plasmons resonances (LSPR) at core/shell particles. Studies have shown that LSPR can be tuned in a wide range of the electromagnetic spectrum by varying the shell thicknesses [^16,20,21,22]. Z. Wang et al. studied theoretically the optical absorption of carbon-core/gold-shell particles with spherical and cubic geometry, focusing on the influence of the shell on the intensity and width of the absorption spectrum [²³]. Others studies have shown that there is an increase of the intensity of the absorption spectrum of core/shell particles compared to pure metal particles [^24,25]. One of the most studied metals in core/shell type nanostructures has been gold combined with a dielectric. Those studies have explained the shift of the absorption band as a function of the relationship between the inner and outer radii of the particle. Studies on the absorption of Au₂S-core/Au-shell have also be done. H. S. Zhou et al. attributed that this shift of position of the LSPR is determined by the quantum confinement of electrons on shell [¹⁹]. On the other hand, R. D. Averitt et al. [²²] attributed it to purely classical behavior that is determined by dimensions and the properties of the core (Au₂S) and the shell (Au), i.e., classical electrodynamics effects, e.g., dependence of the real part of dielectric function (ε) from collective parameter ωp (plasma frequency) and multipolar excitations of the LSPR. It is well known that the dispersive dielectric function of metal depends on the particle’s size. For example, for particles with diameters larger than 10 nm, their dielectric functions are size independent [²⁶], while for particles with a diameter smaller than 10 nm, their dielectric functions are size dependent, i.e., LSPR as function of particle radius must be taken into account [²⁷]. Until now, according to description above, is clear that many studies have been developed to explain the shift position of LSPR as a function of the thickness of shell, e.g., Y. Kim et al. studied the plasmons absorption bands as a function of the shell thickness for gold-core/silver-shell both theoretical and experimentally [²⁸]. However, there are few studies devoted to calculate the near electromagnetic fields for both spheres and core/shell particles, e.g., [^{23,29,30,31,32}].

To the best of our knowledge, there is no report on the calculation of the analytical solution of resonance frequencies in the quasi-static limit as presented in the Eq. (13), for a dielectric-core-/metal-shell and neither a comparison with electrodynamic calculations. Thus, a comparison between the positions of the resonance frequencies of a vacuum-core/Drude-shell particle surrounded by vacuum with both approaches was done. On the other hand, we calculated the distribution of the near electric field from gold-core/silver-shell nanoparticle at fixed wavelength of incident electromagnetic field and we found some differences compared to those reported in the Ref. [³¹].

2 Theory

In this paper, we consider a core/shell nanoparticle (see Fig. 1), with spherical symmetry, in the presence of an incident monochromatic electromagnetic plane wave with the direction of propagation on the positive Z-axis and a polarization of the electric field along the X-axis. The electromagnetic fields are expressed in their multipolar expansion as follows [^33,34]:

where m = 1,2,3 indicates the core, shell and embedded medium, respectively, q_m is the wave number of the medium, Y(l,1)(θ,ϕ) and X→(l,1)(θ,ϕ) are the scalar and vector spherical harmonics, respectively, Z _m is the impedance of the medium, and fl(qmr) and gl(qmr) are the spherical Bessel functions. In the core fl(qmr)=jl(q1r); a(l,1)(-1)=b(l,1)(-1)=0. In the shell fl(qmr)=jl(q2r); gl(qmr)=nl(q2r). And, in the embedded medium fl(qmr)=jl(q3r); gl(qmr)=hl(1)(q3r).

Figure 1 Representation of core/shell particle comprised for two different materials, with R₁ and R₂ the inner and outer radii. ε1, ε2 and ε3 represent the dielectric functions of the core, shell and embedded medium, respectively. The thickness of the shell d = R₂ - R₁.  

An extension of Mie’s theory can be used to calculate the near electric field distribution as well scattering cross section σsca. L. Aden and M. Kerker [²] developed the first analytical solution for the scattering of a plane electromagnetic wave by a core/shell nanoparticle with spherical symmetry. The σsca of a spherical core/shell nanoparticle with inner and outer radii R₁ and R₂, respectively, at a wavelength λ in a vacuum, can be expressed by an infinite series [¹²]:

where a(l,1)(s)=a(l,1)(-3), b(l,1)(s)=b(l,1)(-3) and, q3=2πn3/λ is the magnitude of the wave vector and n₃ is the refractive index of the external medium. The scattering coefficients a(l,1)(s) and a(l,1)(s) are determined by boundary conditions that the fields must satisfy at the inner and outer shell surfaces. a(l,1)(s) and a(l,1)(s) represent the amplitudes of oscillations of magnetic and electric multipole type, respectively. To stablish the convergence for σsca, a wavelength was fixed (at the position of the LSPR) and the calculations were performed as a function of l. The difference between the calculations of σsca carried out with l = 1 and l > 1 were imperceptible because we consider small radius for the particles. In this work, we considered that variations smaller than 1 % are sufficient to establish the convergence of σsca, Eq. (3). In this research paper, l = 1 was necessary.

3 Numerical results

Two different core/shell particles were studied numerically. The first were gold-core/silver-shell nanoparticles and its inverse configuration embedded in vacuum or water. The second particles were vacuum-core/Drude-shell surrounded of vacuum, symmetric configurations. The values of dielectric functions for gold and silver correspond to the bulk metals [³⁵], which were interpolated, and they were calculated to the same wavelength for both metals. We compute the square module of the electric field as a function of r (r > 0, R₁ < r < R₂ and r > R₂) for a fixed wavelength.

All calculations of scattering cross section (σsca) correspond to the dipolar contribution in the Eq. (3), i.e., l = 1.

3.1 Gold-core/silver-shell and silver-core/gold-shell nanoparticles

In Fig. 2, σsca is plotted as a function of wavelength, the LSPR are observed as maxima. When the thickness of the shell is equal to zero, the intensity and wavelength of the LSPR are the same as that calculated with Mie’s theory for a sphere constituted of the core material. The shift of the intensity and position of the LSPR for thickness different to zero can be understood as the interference between the contribution of the LSPR on the core and shell surfaces, causing that σsca to have hybrid behavior and, the contribution of shell surface being the most relevant due to the shell’s skin depth. For gold-core/silver-shell nanoparticles surrounded by vacuum (Fig. 2a)) the increase of the intensity of the LPSR between 330-357 nm (red-shifts) and 517-390 nm (blue-shifts), is associated with the increase of the thickness of silver and it agrees with the reported in literature, e.g., [^31,36,37]. This behavior is the same when the surrounded medium is water (Fig. 2b), but the resonances shift to higher wavelengths, and they are more intense. Other resonance at 365 nm associate to the silver appears for specific thickness, as shown in Figs. 2b) and 2d) (see Table I for more details). In this case (Figs. 2a), 2b)), the real part ε1 of the dielectric function (ε=ε1+iε2) for the silver gives the main contribution in the width and resonance position [ ^27,38], because the imaginary part ε2 is small or its variation in the resonance zone is insignificant. On the other hand, in Figs. 2c), 2d), the contribution of the dissipation energy by the gold shell, i.e., the contribution of the imaginary part ε2 of the dielectric function ε of the gold begins to be relevant [³⁸] causing the damping and decrease of the intensity of LSPR. This behavior is easily illustrated when thickness of gold increase (see Figs. 2c), 2d)). In addition, we suggest that this shift in the intensity of the LSPR for metallic core/shell is directly associated with interference in/out phase of the fields generated in the core and shell surfaces (see Figs. 3a), 3b)). Table I shows the resonance positions for all configurations in Fig.2. For example, when the thickness is 8 nm, the resonance position associated with the shell surface is the same as that of nanoparticle constituted of the shell material and with lower intensity as shown in Fig. 2.

Table I Resonance positions as a function of thickness for metallic core/shell nanoparticles.  

Thickness (nm)	LSPR positions (nm) in vacuum
	gold-core/silver-shell		silver-core/gold-shell
0	517	ND*	357	ND*
2	494	336	364	494
4	379	345	368	502
6	375	354	ND*	515
8	ND*	357	ND*	517
Thickness (nm)	LSPR positions (nm) in water
	gold-core/silver-shell		silver-core/gold-shell
0	525	ND*	365; 400	ND*
2	496	336	365; 404	496
4	488	365; 395	365; 406	517
6	ND*	365; 398	ND*	521
8	ND*	365; 400	ND*	525

ND*: None Defined

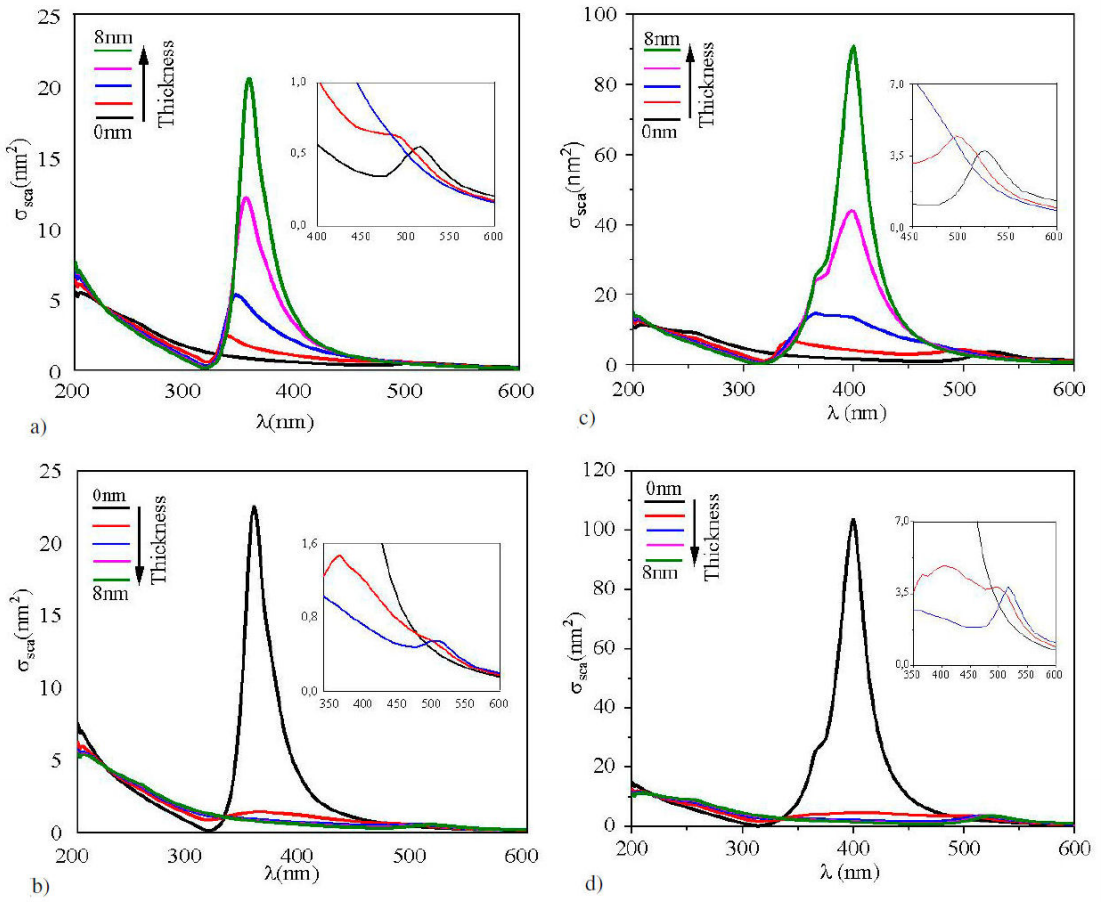
Figure 2 Scattering cross section as a function of the wavelength for core/shell nanoparticles, the outer radius was fixed at 10 nm. a) and c) gold-core/silver-shell, thickness from bottom-up. b) and d) silver-core/gold-shell, thickness from top- bottom. a) And c) surrounded by vacuum, b) and d) surrounded by water (n = 1.33). The thicknesses d of the shell was of 0, 2, 4, 6 and 8 nm, respectively, in all figures. Insets show resonances amplification for configurations with thickness of 0, 2 and 4 nm, respectively.  

Figure 3 a) Projection on the Z - X plane of the square module of electric field at 354 nm (resonance in Fig. 2a) near to core/shell particle, b) at 387 nm and c) at 620 nm, out resonance. The white circles represent the limits between the different materials: core/shell and shell/embedded medium. Values of wavelengths were taken from scattering cross section of a gold-core (4 nm)/silver-shell (6 nm) nanoparticle, magenta line in Fig. 2a).  

The distribution of near electric field (NEF), i.e., the square module of electric field, for a fixed wavelength is shown in Fig. 3. The spatial distribution of NEF was possible due to compute of all coefficients of electromagnetic fields in the core, shell and embedded medium. The Fig. 3 shows that the square module of electric field is maximum near to outer shell and core surfaces, as shown in Fig. 4a). In fact, this is very interesting because the field decays sharply inside the shell and core surfaces.

Figure 4 Projection along Z-axe of the square module of electric field. a) For X=0 and b) for X=10 nm. We take this projection from Fig. 3a).  

However, in the direction of polarization of the electric field, i.e., X-axes, the maximum value on the core surface (63.14) is only three units less compared with the maximum value on the shell surface (66.4) -the values inside the parenthesis were taken from the data in Fig. 3a). In this sense, the NEF intensity generated on the gold core surface (4 nm radius), as consequence of the decay (in the direction of the polarization of the electric field) inside of the shell is almost three times greater than the intensity (19.5) generated by a gold sphere (see Table II). One clear evidence of the fact that the maximum value of the near field intensity is maximum in the direction of polarization of the electric field can be seen in the Fig. 4b). In this sense, our results disagree with those reported by C. Zhang et al. [³¹]. e.g., Figs. 4a), 4c), 10b, 10d, show that the near electric field value is not maximum on outer metal shell surfaces and, this cannot be possible.

Table II Maximum value of |E/E0|2 as a function of a fixed wavelength. The displayed values correspond to the resonance wavelengths in the indicated configurations. The radius of the silver core nanoparticle was fixed at 10 nm. The vacuum as a surrounded medium.  

Au shell thickness (nm)	λ (nm) of maximum in σsca	2*|E/E0|2
0.0	357	124.0
0.2	358	67.60
0.5	360	39.40
1.0	362	24.10
1.5	363	18.05
2.0	363	14.95
10.0*	517	19.15

*This value corresponds to a gold sphere with 10 nm radius.

Our results suggest that the calculations developed by C. Zhang et al. may underestimate the coefficients in the core and shell for the fields -the asymmetric distribution of the near electric field around the center of the particle in Figs. 3c), 3d); black holes in Figs. 3b), 10d) could validate our appreciation. Furthermore, the NEF value for the same configuration cannot be equal for a resonance wavelength in the cross sections and another out of resonance, as shown in Ref. [³¹]. In addition to these features of the NEF, our data also exhibit that it decays approximately as e-aR2 and e-bd outer shell and core, respectively, and sharply within them as expected as shown in Fig. 4a). It could be very helpful, e.g., for applications in efficiency from Raman activity as a function of the distance at which the target is located with respect to the shell surface.

On the other hand, the intensity of near electric field is proportional to the scattering cross section intensity, as shown in Fig. 3, and this agrees with the reported by B.J. Messinger et al. [²⁹] e.g., at resonance wavelength (354 nm) (Fig. 3a)), the near electric field intensity is about five times larger than out of resonance (620 nm) (Fig.3c)). The incident electromagnetic wave causes an enhancement on shell surface, but not on the core surface, as shown in Fig. 3c).

Table II shows the maximum value of the NEF intensity for gold thickness from 0 to 2 nm, keeping the silver core radius fixed at 10 nm. The quantum confinement was not considered. This was done to determine how much the intensity of the fields varied for small shell thicknesses. The maximum value of |E/E0|2 of all different configurations corresponds to that of a silver sphere: about of six time larger than the value for a gold sphere. Thus, an alternative (according to the data in Table II) for potential applications like the surface-enhanced Raman scattering (SERS), which has great importance in different areas such as medical diagnostic [³⁹], is the use of silver-core/gold-shell nanoparticles due to their efficiency to generate higher intensity of the LSPR, instead of by using gold nanoparticles.

In summary, gold-core/silver-shell nanoparticles present more variation of the optical properties. It is possible to have a control over the intensity as well the resonance wavelength position. This control could be very helpful for applications in efficiency from Raman activity [^39,40], energy transfer to the adsorbed species to enhance the photo-catalytic process [⁴¹] and fluorescent molecules located on or near to surface of noble metals [^42,43]. The maximum value of the square module of the electric field is located on the outer metal surfaces in the direction of the incident electric field and its spatial distribution is like that of an electric dipole.

4 Resonance frequencies in quasi-static limit for a vacuum-core/Drude-shell particle surrounded by vacuum

When the magnitude of wave vector k=(ω/c)→0 , the Helmholtz’s equation becomes Laplace’s equation, therefore, the temporal variation of the fields can be omitted. So, under these considerations, the problem of a core/shell particle in the presence of a uniform electric field with a direction in the positive Z-axis is solved. It is summarized into finding the solution to the Laplace’s equation for the potential scalar Φ(r,θ), i.e., ∇2Φ(r,θ)=0. For the azimuthal symmetry, the solution can be written as follows:

The coefficients a _l and b _l are found by using boundary conditions of electric potential, Eq. (5), and the orthogonally properties of Legendre Polynomial’s. The boundary conditions are:

where εi (i =1,2,3) is the dielectric constant of the core, shell and embedded medium. By replacing the equation for the potential in the boundary conditions, Eqs. (5), and by using the orthogonally conditions of Legendre’s polynomials we find the solutions on each region:

where

The resonance conditions for the potential in the Eq. (8) are given when the denominator q⁽⁺⁾ (Eq. (10)) has its minimum value, i.e., it is zero. Our interest is focused in the case when the core and embedded medium is the vacuum, i.e., ε1=ε3=1. So, Eq. (9) becomes:

ε2 is represented for the Drude‘s model:

where ε∞ is the high-frequency limit of the dielectric function, ωp is the Drude plasma frequency and γ is the damping constant. So, by replacing Eqs. (11) and (12) into Eq. (10) and by making zero the last one, we find the resonance frequencies ωr±:

where f=(R1/R2)3 is the filling ratio. When f = 0,1 this represents one sphere constituted of the shell and core material, respectively, i.e., silver and vacuum. If we assumed that γ=0, it is possible to find two limit cases:

For f = 0:

For f = 1:

It is well known that for R≪λ (R = R₂) both theories electrodynamic and quasi-static limit present comparable results. However, to the best of our knowledge there is not report of the analytical solution for the calculation of the positions of the resonance frequencies in the quasi-static limit (Eq. (13)), which is easier to use in comparison with electrodynamic calculations. Figure 5 shows a comparison between the positions of resonance frequencies obtained with the quasi-static limit, Eq. (13), and ones calculated with electrodynamic, scattering cross section (Eq. (3)). The Drude’s model, Eq. (12), was used for the description of dielectric function for the shell (silver). For all calculations, the parameters ε∞=4.039; ωp=9.1721 eV; γ=0.0207 eV [³⁸] were used. In both quasi-static limit (circles on the red lines) and electrodynamic (triangles to the right on the black lines) represented by Eqs. (13) and (3), respectively, they predict two resonance frequencies ( ωr- and ωr+) for each f (except f = 0, in the electrodynamic case). These resonance frequencies are associate to the interaction of the incident wave with electrons on the two interfaces: core/shell (ωr+) and shell/embedded medium (ωr-). Figure 5 shows that ωr+ varies slowly between two consecutive f, reaching its maximum value of 4.55 eV for f = 0.9 in all external radius from 10 to 30 nm -in this work we only show results for R₂ = 10 (Fig. 5a)), 20 and 30 nm (Fig. 5b))-. We associate these resonances with the discontinuity produced by the presence of the metal shell in the propagation of the electromagnetic field. In fact, the value 4.55 eV is very close to (ωp2/ε∞)-γ2, i.e., the frequency at which the real part of ε given for Eq. (12) is zero. On the other hand, ωr- represent the LSPR on the outer shell more the contribution of the resonance on the core/shell surfaces.

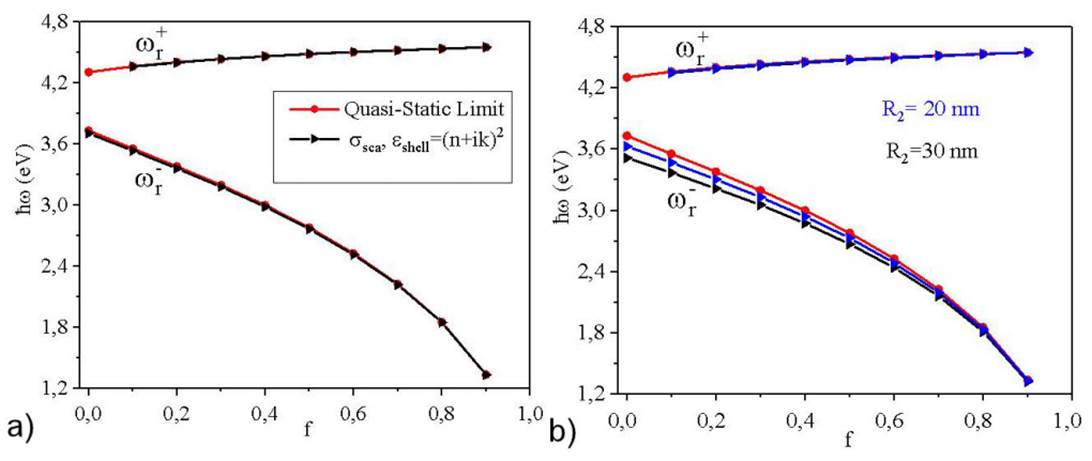
Figure 5 The resonance frequencies as a function of the filling ratio. a): Comparison between the positions of resonance frequencies obtained with the quasi-static limit (Eq. (13)) -circles on the red lines- and ones calculated with electrodynamic (Eq. (3))-triangles to the right on the black lines- for vacuum-core/silver-shell nanoparticles as a function of f for R₂ = 10 nm fixed. b): triangles to the right on the blue and black lines are the resonance frequencies predicted from electrodynamic theory, for R₂ = 20, 30 nm, respectively.  

The results given for the electrodynamic theory are in good agreement with predicted by quasi-static limit as shown in Fig. 5a), i.e., when the dielectric function keeping the damping constant γ in the Eq. (12).

In this case, the positions of the resonance frequencies predicted by Eq. (13) have higher values that given for Eq. (3) for all values of f with a maximum error of 0.66% between both theories when f = 0. For f = 1 both theories give the same results, ωr-=0 (this value is not shown in Fig. 5 for visual details). This is obvious since Eqs. (10), (11) are equals to nine and one, respectively, and Eqs. (6), (7) and (8) become -E0rcosθ, that is the electric potential associated to the electric field in a linear, isotropic, and homogeneous medium, in this case, the vacuum. The same situation happens in the electrodynamic theory. In addition, when the external radius is increased, the results obtained from electrodynamic theory differ considerably from the ones using the quasi-static limit. For example, Fig. 5b) shows that for an external radius of 20 nm the resonances frequencies ωr- predicted by electrodynamic theory for f < 0.8 begin to differ significantly from those predicted by the quasi-static limit, with a maximum error of 2.67%, for f = 0. This error increases when R₂ = 30 nm, to 5.75 %. Thus, the resonance frequencies calculated with both theories with values closer to each other, are given for the configurations with an outer radius of 10 nm and, under these conditions the quasi-static limit can be used instead of electrodynamic calculations.

5 Conclusions

A study of the diffraction of a monochromatic electromagnetic plane wave from a core/shell particle was presented. It was demonstrated that for metallic core/shell configurations the interference of electric field produced on core/shell surfaces modified the scattering cross section in comparison with one sphere of core and shell material, respectively. The gold-core/silver-shell nanoparticles are those that present more variation of the optical properties, and it is possible to have a control over the intensity as well as the resonance wavelength position. When the metallic core/shell nanoparticle is surrounded by a medium with higher refractive index (water) the resonance positions shift to higher wavelengths in comparison with vacuum. We have shown that electrons in the two interfacial zones respond to an external field generating an enhancement of the near field on the outer metal surfaces and, its maximum value is located on the direction of polarization of the incident electric field. Furthermore, it decays approximately as e-aR2 and e-bd outer shell and core, respectively; this could be very helpful for applications in efficiency from Raman activity [^39,40], energy transfer to the adsorbed species to enhance the photo-catalytic process [⁴¹] and fluorescent molecules located on (near) the surface of noble metals [⁴³]. In addition, the spatial distribution of NEF of a gold-core/silver-shell nanoparticle is like that of an electric dipole. Second, for the vacuum-core/Drude-shell nanoparticles surrounded by vacuum, we found that the positions of resonance frequencies predicted by both theories quasi-static limit and electrodynamic are in good agreement when the damping constant of the metal shell is considered in the dielectric-Drude function. In this sense, the resonance values are almost equals for the configurations with outer radius of 10 nm. Thus, the quasi-static limit can be used for calculating the positions of resonance frequencies of vacuum-core/metal-shell, when external radius is smaller than 20 nm with error less than 3 % between both theories.