1. Introduction
Potential models have been used to model several phenomena right from the early days of quantum mechanics and its related disciplines. It has been used to model interatomic interactions in diatomic molecules, quantum dots, quarkonium interactions, plasma, etc. [1]. Debye and Huckel suggested a theory [ 2] in 1923 that plasmas could be described theoretically with the well-known screened Coulomb potential. This potential provides a cutting-edge plasma treatment through the screening effect. This model is aimed to simulate the plasma screening effect for weakly coupled plasmas. Its potential is given by [3]:
A thoughtful presentation by Shukla and Eliasson [4] showed that the modified Debye-Huckel potential, also known as the exponential-cosine-screened Coulomb potential,
In another consideration, Yoon and Yun [5] proposed that the well-known Hulthen potential [6]:
When plasma density is intensified adequately, quantum effects become very fascinating. This includes degeneracy effects, which becomes important when T > T
F
, where T is the plasma temperature,
In plasmas, in order to further improve these models, the electron spin is taken into account, which introduces a magnetic dipole force, spin precession, and spin magnetization currents into the picture [9]. However, in the present consideration the vector potential comprising of magnetic and Aharanov-Bohm fields and topological defect are introduced.
In fact, there has been an increasing interest in plasmas of low-temperature and high densities, where quantum properties tend to be important [10]. Promising applications include spintronics [11] and plasmonics [12]. Quantum plasma effects can also be of interest in experiments with solid density targets [13]. Important classifications of dense plasmas include whether they are strongly or weakly coupled, and whether they are degenerate or nondegenerate [9].
We have sufficient resources to research the hydrogen atom in weakly coupled quantum plasmas under the influence of an Aharonov-Bohm (AB) flux field and a uniform magnetic field with topological defects, based on the information we have gathered. In non-relativistic quantum mechanics and quantum field theory, the hydrogen atom stands out as a straightforward dual-body problem with an empirical closed form solution [3,14,15]. When studying quantum effects in very complicated structures, a thorough understanding of its basic structure is critical.
Numerous papers [7-18,16] have investigated the effects of an external electric and magnetic field on the hydrogen atom. We propose that, in addition to using AB and magnetic fields to regulate the energy levels or localization of a hydrogen atom’s quantum state in quantum plasmas, the topological defect could be used.
We show in this paper the effect of topological defect and other external fields. This paper is an extension of the works of Bahar et al. [7] and Falaye et al. [8]. Both articles considered the hydrogen atom in Minkwoski space but in the present study, we have taken a step forward to consider the effect of a defect in the medium. In various areas of physics, such as gravitation [17], condensed matter physics [18], etc., the study of the effect of topology on the physical properties of various systems has been of critical relevance and this has been greatly studied by several authors [19-37]. Hydrogen atom has been studied in a medium with topological defect by several authors [38-39].
As a result, it is critical to investigate the effect of disclination on hydrogen atoms in a quantum plasma system with AB and magnetic fields. However, we would like to conduct this research using the Hulthen potential model of the form;
where the parameter η is a consequent of the topological defect. The effects of these two external fields on a hydrogen atom with a topological defect in a weakly coupled quantum plasma was investigated in this article. As a result, we expect this research would be useful in fields such as atomic structure and plasma collisions, as well as astrophysics.
2. Theory and calculations
Consider the hydrogen atom in a quantum-plasma system, where the AB and
Where 0 < η < 1 is the parameter associated with the deficit of angle. The parameter η is related to the linear mass density
The Schrödinger equation for this consideration is given as follows, bearing in mind the presence of the perturbing fields and defect:
Where E
nm
represents the energy level, μ is the effective mass of the system. The Laplacian used is defined as follows with Topological defect as [39,40]. The vector potential, denoted by
The parameter η represents the influence of the topological defect in the region. We assume a wave function in cylindrical coordinates as
Where V eff (r) is the effective potential defined as follows;
where
where we have introduced the following dimensionless notations:
for mathematical simplicity. We assume the following ansatz of the form:
where
By substituting Eq. (8) into Eq. (7), we obtain a hypergeometric differential equation and by extension the quantization condition as follows:
By making ε nm the subject of the expression by carrying some simple manipulative algebra, we get:
As a result, if the value of the dimensionless parameters in Eq. (7) is substituted into Eq. (11), the following solutions are obtained:
For the sake of completeness, we continue to find the system’s wave function [46,47]. The corresponding unnormalized wave function is obtain as
Finally, the corresponding wave function is obtain as
3. Discussions
Table I shows the eigenvalues of the hydrogen atom in the presence and absence of external fields (the magnetic field and the AB flux field) as well as topological defects in a.u. and low vibrational n and rotational m. From the table, we see that when the external fields and defect are absent (i.e., when
Table I Energy values for the hydrogen atom in weakly coupled quantum plasma in the presence of topological defect and under the influence of AB flux and external magnetic fields with various values of magnetic quantum numbers. The following fitting parameters have been employed: Z = 1, λ D = 20, and note that η = 1 means absence of topological defect. All values are in a.u.
| m | n |
|
|
|
|
|
|---|---|---|---|---|---|---|
| 0 | 0 | -2.0003100 | -0.0004239 | 0.0286131 | -80000.0000000 | -8.0003100 |
| 1 | -0.2008680 | -0.0023947 | 0.0255455 | -8884.4500000 | -0.8453130 | |
| 2 | -0.0581125 | -0.0067716 | 0.0215986 | -3195.2000000 | -0.2741130 | |
| 3 | -0.0203125 | -0.0134862 | 0.0168847 | -1627.7600000 | -0.1182720 | |
| 1 | 0 | -0.1892010 | -0.0011606 | 0.0340070 | 9.4772400 | -0.2403120 |
| 1 | -0.0535125 | -0.0055494 | 0.0296653 | 9.4304300 | -0.0998023 | |
| 2 | -0.0176594 | -0.0122754 | 0.0246875 | 9.3818200 | -0.0437076 | |
| 3 | -0.0046335 | -0.0212736 | 0.0190781 | 9.3314500 | -0.0171720 | |
| -1 | 0 | -0.1892010 | 0.0003276 | 0.0194406 | 9.4772400 | -0.2403120 |
| 1 | -0.0535125 | 0.0008224 | 0.0193156 | 9.4304300 | -0.0998023 | |
| 2 | -0.0176594 | -0.0011606 | 0.0172911 | 9.3818200 | -0.0437076 | |
| 3 | -0.0046335 | -0.0055494 | 0.0139986 | 9.3314500 | -0.0171720 | |
| m | n |
|
|
|
|
|
| 0 | 0 | -0.000325 | 0.024481 | -0.003968 | -0.080440 | |
| 1 | -0.001807 | 0.029688 | -0.017579 | -0.102965 | ||
| 2 | -0.005710 | 0.030932 | -0.033278 | -0.127357 | ||
| 3 | -0.011965 | 0.029688 | -0.051010 | -0.153571 | ||
| 1 | 0 | -0.015141 | 0.057465 | -0.004637 | -0.146217 | |
| 1 | -0.025820 | 0.053667 | -0.020448 | -0.175629 | ||
| 2 | -0.038665 | 0.048884 | -0.038289 | -0.206750 | ||
| 3 | -0.053618 | 0.043248 | -0.058110 | -0.239544 | ||
| -1 | 0 | -0.015550 | -0.077864 | -0.003286 | -0.0317934 | |
| 1 | -0.006469 | -0.029201 | -0.014657 | -0.046653 | ||
| 2 | -0.000125 | -0.006428 | -0.028174 | -0.0635686 | ||
| 3 | 0.003565 | 0.004717 | -0.043780 | -0.0824881 | ||
The energy values are reduced and degeneracies are removed when the system is only exposed to the AB flux field, but the pseudo-degeneracies among the states are unaffected. As the quantum number n increases for fixed m, the energy levels become more positive and the system becomes strongly positive. When only the topological defect is present, the degeneracies and pseudo-degeneracies are unaffected, and the total interaction potential becomes more attractive. The energy level is also shifted upwards by the topological defect.
In the absence of a topological defect, the combined effect of the magnetic and AB fields is greater than the individual effects and the absence of the fields. There is a significant change in energy levels, which we notice. When there is only a magnetic and topological defect, the effect is also great, and there is a significant shift in energy levels, but it is less than when the fields are present alone. When there is only the AB field and a topological defect, the effect is also great, with a significant shift in energy levels, but it is less pronounced than in the previous two cases. The total impacts suggest that the system is highly repulsive. Furthermore, the mutual effect (triad) of the fields and topological defect is greater than the individual and dual effects, resulting in a significant shift in the system’s bound state energy.
Figure 1 shows the plot of the effective potential energy to simulate weakly coupled quantum plasmas environment with rotational (m = 1) levels for various values of λ
D
with ξ = 6 , η = 0.004, and
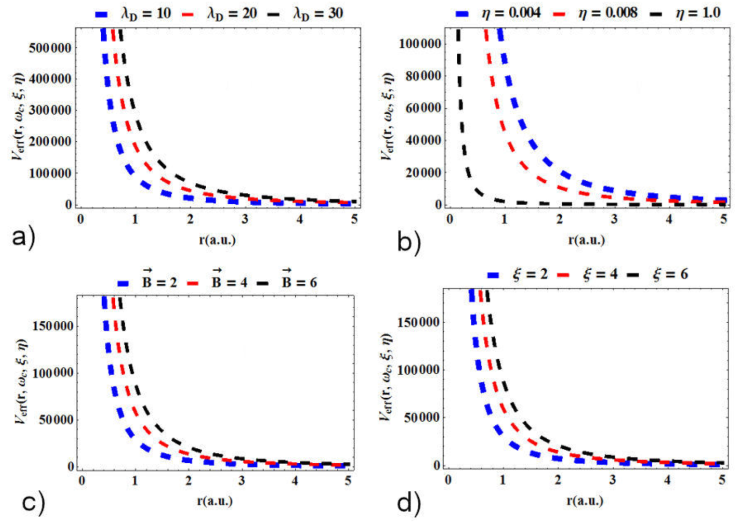
Figure 1 Effective potential energy to simulate weakly coupled quantum plasmas
environment with rotational (m = 1) levels for a)
various values of λ
D
with ξ = 6, η = 0.004 and
Figure 2 shows the effective potential energy to simulate weakly coupled quantum plasmas environment with rotational (m = 1) levels.
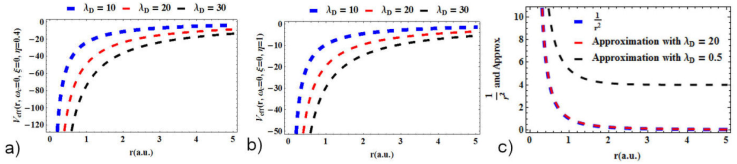
Figure 2. Effective potential energy to simulate weakly coupled quantum plasmas environment with rotational (m = 1) levels for a) for various values of λ D with η = 0.004. b) Same as a) but with η = 1. c) The approximation used is plotted to show the validity. All our computations are in a.u.
Figure 2a) presents various values of λ D with η = 0.004. The effective potential increases as the inter-nuclear distance increases. Figure 2b) shows the same as a) but with η = 1. The behaviour remains the same, indicating that the presence or removal of the defect has little impact on the result. In 2c), the approximation used is plotted to show the validity. The approximation is only valid for large λ D . For this reason, we choose λ D ≥ 20 where necessary in our computation. We see that for large λ D , the centrifugal term is well-approximated.
Figure 3 shows the variation of energy values for the hydrogen atom in quantum plasmas and under the influence of the magnetic field and the AB flux field with topological defect in atomic units using the fitting parameters m = n = 0 and λ
D
= 20. In 3a), the energy is plotted as a function of external magnetic field in the region 0 <
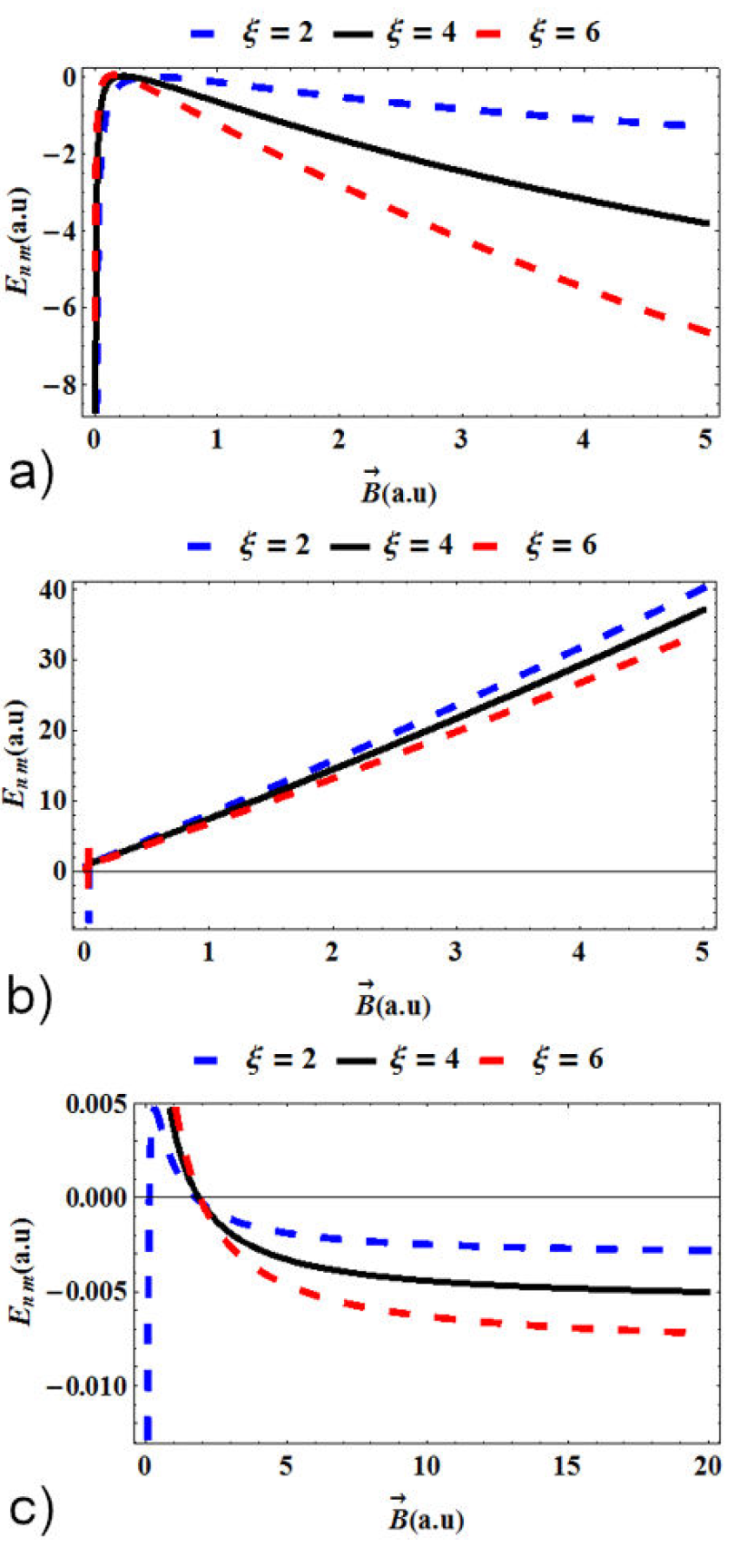
Figure 3 Variation of energy values for the hydrogen atom in quantum plasmas
and under the influence of the magnetic field and the AB flux field with
topological defect in atomic units using the fitting parameters
m = n = 0 and λ
D
= 20
Figure 4 shows the variation of energy values
for the hydrogen atom in quantum plasmas and under the influence of the magnetic
field and the AB flux field with topological defect in atomic units using the
fitting parameters m = n = 0 and
λ
D
= 20. In Fig. 4a), the energy is plotted as a function of the topological
defect with various ξ and a fixed magnetic field,
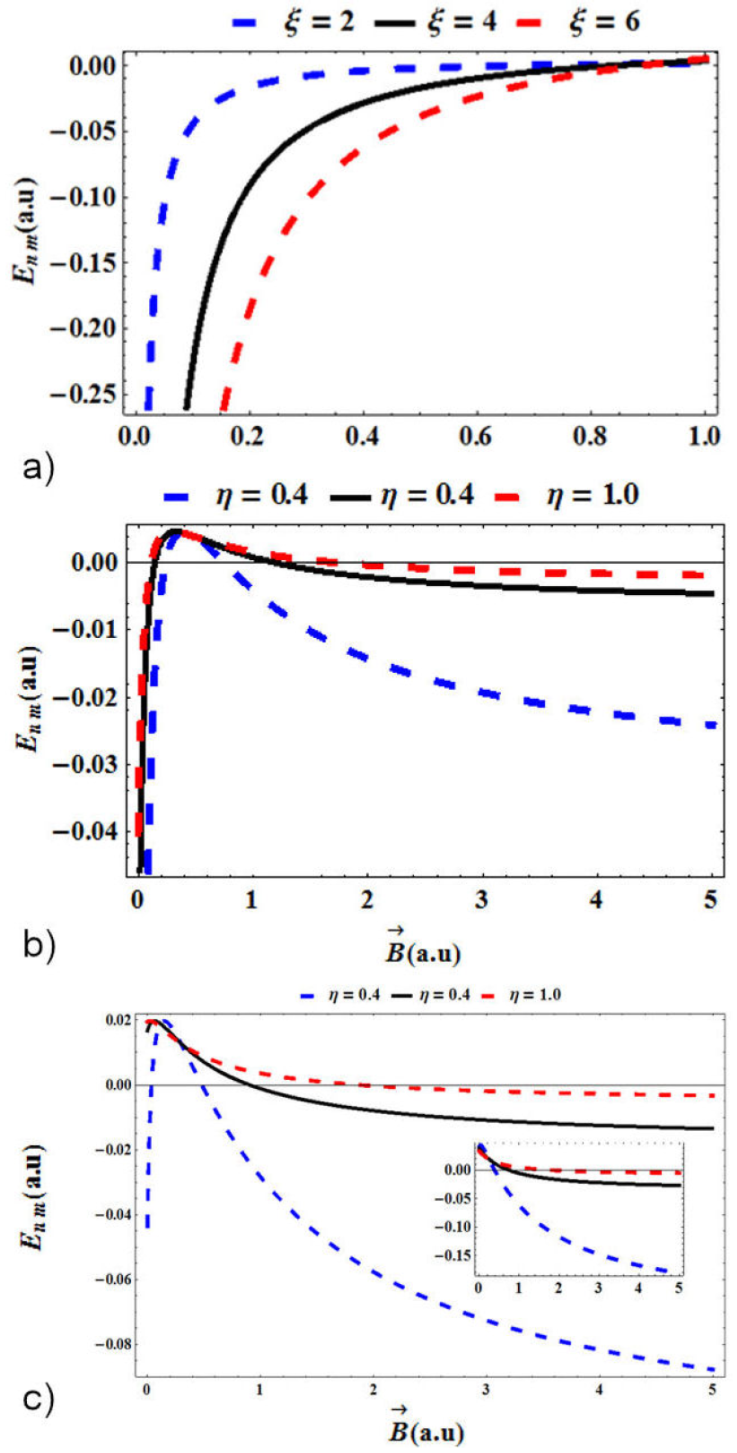
Figure 4 Variation of energy values for the hydrogen atom in quantum plasmas
and under the influence of the magnetic field and the AB flux field with
topological defect in atomic units using the fitting parameters
m = n = 0 and λ
D
= 20
Figure 5 shows the magnetic field versus inter-particle distance. The magnetic field is seen to increase with increasing interparticle distance monotonically.
4. Conclusion
For the first time in a quantum plasmas environment, we have considered the effects of the AB flux, uniform magnetic field, and topological defect on the hydrogen atom in this research paper. The complete effects indicate that the system is highly attractive, while quantum level localizations alter and eigenvalues decrease. Furthermore, as we have shown, the total effect of the fields is greater than the sum of the individual effects, resulting in a large change in the system’s bound state energy. Although the magnetic field will act as a controller or boost, the topological defect and AB field are needed to keep the hydrogen atom in quantum plasmas at a low energy. The findings of our research may be extended to atomic structure and plasma collisions.











 nueva página del texto (beta)
nueva página del texto (beta)



