Introducción
La respuesta de las estructuras ante eventos sísmicos siempre ha sido objeto de estudio debido a las implicaciones que tienen los daños o el colapso de las estructuras. Debido a ello, han surgido soluciones novedosas, como el uso de amortiguadores sísmicos, y se han propuesto varios métodos de diseño de estructuras para la reducción de los daños ante estos eventos (Symans y Constantinou, 1998, Terán y Virto, 2009; Ruiz, 2018). Entre los métodos de diseño de estructuras equipadas con amortiguadores sísmicos destacan el de ASCE 41-17 (2017) y el de Christopoulos y Filiatrault (2006). Estos métodos se basan en calcular niveles de amortiguamiento objetivo que permiten controlar la respuesta lateral de las estructuras, para luego calcular las propiedades de amortiguadores lineales y, a su vez, convertir dichas propiedades en propiedades equivalentes de amortiguadores no lineales.
Dados los daños que se han observado en sismos pasados (ej. Pujol and Rodríguez, 2019; Buendía y Reinoso, 2019), ha surgido interés por emplear dispositivos de protección sísmica para disminuir la respuesta lateral de las estructuras ante sismos. Estos dispositivos se pueden clasificar en pasivos, control híbrido o control semi-activo, y control activo (Soong y Dargush, 1997; Spencer y Soong, 1999; Gómez et al., 2008, Taylor, 2003). En años recientes se ha investigado sobre un tipo de dispositivos pasivos de protección sísmica, los amortiguadores viscosos lineales (Constantinou y Symans, 1992) y no lineales (Seleemah y Constantinou, 1997). Estos dispositivos trabajan disipando energía sísmica para reducir los daños a las estructuras (Symans et al., 2008) y son llamados dispositivos dependientes de la velocidad (VDD, por sus siglas en inglés), pues dependen de la velocidad relativa en sus extremos para poder disipar energía (Ruiz, 2018). En la Figura 1 se muestra el esquema general de un amortiguador viscoso, compuesto principalmente por un cilindro metálico, un pistón metálico (cuya cabeza cuenta con orificios que permiten el paso del fluido compresible de una cámara del cilindro a otra), fluido compresible y las placas de conexión en los extremos.
Cuando un movimiento sísmico ocurre, la energía de entrada al sistema estructural se transforma en energía cinética, se almacena en forma de energía elástica, y se disipa en forma de energía inelástica y de amortiguamiento. El balance energético se puede expresar, según Symans y Constantinou (1998), como:
donde t es el tiempo,
En este artículo se estudian los amortiguadores viscosos no lineales. Para representar el comportamiento de este tipo de amortiguadores se usa un modelo matemático que está dado por la relación fuerza-velocidad de Symans et al. (2008). Esto es:
donde
El cálculo del coeficiente de viscosidad,
donde
siendo
Respuesta de estructuras equipadas con amortiguadores no lineales
La idea de usar amortiguadores viscosos no lineales es obtener los mismos niveles
de amortiguamiento que los amortiguadores lineales, pero con fuerzas de
amortiguamiento menores en los dispositivos y sus conexiones (Lin y Chopra, 2002; Seleemah y Constantinou, 1997; Terenzi, 1999). Esto resulta conveniente porque, al tener
fuerzas menores, se evitan daños a los disipadores y sus conexiones a la
estructura. Además, se puede optimizar el diseño de los elementos de soporte, y
tener mayor certidumbre sobre el diseño, pues la probabilidad de que la fuerza
máxima del dispositivo no exceda su valor de diseño es muy alta. En la Figura 2 se muestra el comportamiento de la
fuerza de amortiguamiento, F
D
, en función del desplazamiento, u, y del exponente de
la velocidad,
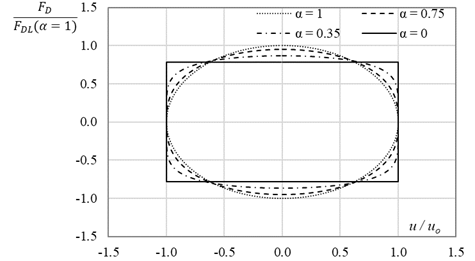
Figura 2. Curvas de histéresis para amortiguadores de fluidos viscosos (adaptado de Lin y Chopra, 2002).
En un estudio realizado por Moreno (2019), sobre estructuras equipadas con amortiguadores viscosos lineales y no lineales, se demostró que existen diferencias significativas entre la respuesta de estructuras equipadas con estos amortiguadores. A manera de resumen, las Figuras 3a y 3b muestran, respectivamente, relaciones de desplazamiento en azotea y de fuerzas de amortiguamiento en los dispositivos, calculadas para el movimiento sísmico SCT-EW 19/09/1985. Estas relaciones fueron calculadas como el cociente de la respuesta máxima de estructuras lineales equipadas con amortiguadores no lineales (α < 1) entre aquella de estructuras lineales equipadas con amortiguadores lineales (α= 1). Se consideró un amortiguamiento suplementario (es decir: adicional), proporcionado por los amortiguadores, ya sean lineales o no lineales, equivalente al 30% del amortiguamiento crítico. Mientras las curvas presentan relaciones calculadas a partir de osciladores de un grado de libertad, los puntos corresponden a las relaciones de estructuras de varios grados de libertad. Se puede apreciar que son significativamente diferentes de la unidad, lo que implica que las respuestas de estructuras equipadas con amortiguadores lineales y no lineales son muy diferentes. Esto sugiere que diseñar estructuras para alcanzar un amortiguamiento lineal dado, para luego usar amortiguadores no lineales, puede resultar en un comportamiento estructural diferente al esperado. Dadas las diferencias tan significativas observadas, este artículo propone una metodología simple para diseñar estructuras equipadas con amortiguadores viscosos no lineales. La metodología se basa en el control de los desplazamientos laterales de un oscilador equivalente de un grado de libertad y coeficientes de desplazamiento que toman en cuenta la no linealidad de los amortiguadores y los efectos de varios grados de libertad.
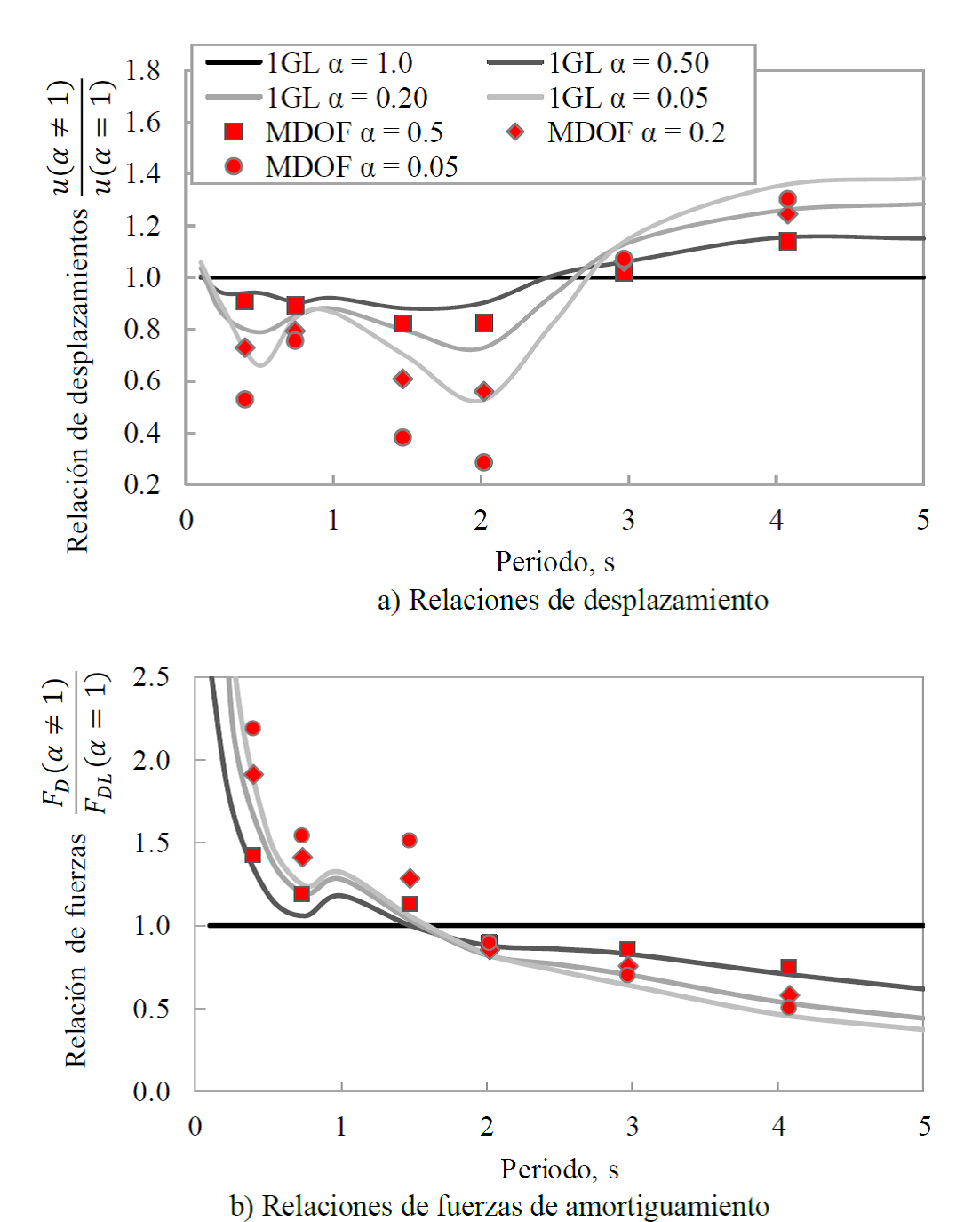
Figura 3. Relaciones de desplazamiento y fuerza en amortiguadores lineales y no lineales (después de Moreno, 2019)
Coeficientes de desplazamiento propuestos
En esta sección se definen dos coeficientes de desplazamiento que permiten tomar en cuenta el efecto de la no linealidad de los amortiguadores viscosos y el cambio de uno a varios grados de libertad en las estructuras. Para calcularlos, se realizaron análisis dinámicos no lineales, para varios movimientos sísmicos, en osciladores de un grado de libertad y en estructuras de VGDL con diferente número de niveles.
Movimientos sísmicos considerados
Para realizar los análisis de esta investigación se usaron los 30 movimientos sísmicos de la Tabla 1, originalmente utilizados en un estudio de Bojórquez y Ruiz-García (2013). Estos se seleccionaron por haber sido registrados en el suelo blando de la Ciudad de México y por ser los de mayor intensidad según la Base de Datos Mexicana de Sismos Fuertes (BDMSF, 1999). A los movimientos se les realizó un filtrado tipo pasabanda entre 0.1 y 20 Hz con ayuda del programa PRISM (2012). En la Tabla 1 se presenta la estación donde se registró el sismo, la fecha en que sucedió, la magnitud, la componente utilizada, el periodo dominante del suelo (T g ), el paso del tiempo (dt) y la aceleración máxima del suelo (A max ).
Tabla 1. Características de los movimientos sísmicos seleccionados.
| Registro | Estación | Fecha | Magnitud | Componente | T g (s) | dt (s) | A max (cm/s²) |
| 1 | AL01 | 25/04/1989 | 6.90 | NS | 2.08 | 0.005 | 127.48 |
| 2 | AL01 | 15/06/1999 | 6.60 | NS | 1.88 | 0.005 | 149.42 |
| 3 | BL45 | 20/03/2012 | 7.50 | NS | 1.96 | 0.010 | 178.36 |
| 4 | BL45 | 25/04/1989 | 6.90 | NS | 2.34 | 0.005 | 165.34 |
| 5 | CA59 | 25/04/1989 | 6.90 | NS | 3.18 | 0.005 | 148.06 |
| 6 | CCCL | 07/09/2017 | 8.20 | EO | 1.42 | 0.010 | 163.97 |
| 7 | CH84 | 07/09/2017 | 8.20 | EO | 1.40 | 0.010 | 139.75 |
| 8 | CJ03 | 20/03/2012 | 7.50 | NS | 1.96 | 0.010 | 149.64 |
| 9 | CJ04 | 14/09/1995 | 7.30 | NS | 2.04 | 0.010 | 140.72 |
| 10 | CJ04 | 15/06/1999 | 6.60 | EO | 1.68 | 0.010 | 155.51 |
| 11 | CO56 | 14/09/1995 | 7.30 | ND | 2.34 | 0.010 | 145.40 |
| 12 | GA62 | 14/09/1995 | 7.30 | ND | 2.02 | 0.010 | 134.95 |
| 13 | GA62 | 30/09/1999 | 7.40 | NS | 1.92 | 0.010 | 142.39 |
| 14 | JA43 | 14/09/1995 | 7.30 | ND | 3.02 | 0.005 | 152.51 |
| 15 | JC54 | 07/09/2017 | 8.20 | NS | 1.22 | 0.010 | 127.65 |
| 16 | LI58 | 25/04/1989 | 6.90 | ND | 2.22 | 0.010 | 171.65 |
| 17 | LI58 | 25/04/1989 | 6.90 | NS | 2.32 | 0.010 | 200.26 |
| 18 | PCJR | 07/09/2017 | 8.20 | EO | 2.12 | 0.010 | 112.72 |
| 19 | PCJR | 07/09/2017 | 8.20 | NS | 2.22 | 0.010 | 177.35 |
| 20 | SCT1 | 19/09/1985 | 8.10 | NS | 2.06 | 0.010 | 154.46 |
| 21 | SCT2 | 20/03/2012 | 7.50 | NS | 1.86 | 0.010 | 147.73 |
| 22 | SCT2 | 07/09/2017 | 8.20 | EO | 1.70 | 0.010 | 158.67 |
| 23 | SCT2 | 15/06/1999 | 6.60 | NS | 1.88 | 0.005 | 151.45 |
| 24 | SCT2 | 15/06/1999 | 6.60 | NS | 2.04 | 0.005 | 146.49 |
| 25 | TH35 | 15/06/1999 | 6.60 | NS | 1.76 | 0.005 | 143.98 |
| 26 | TH35 | 30/09/1999 | 7.40 | NS | 1.90 | 0.005 | 144.38 |
| 27 | TL08 | 20/03/2012 | 7.50 | NS | 1.86 | 0.010 | 188.51 |
| 28 | TL55 | 25/04/1989 | 6.90 | NS | 2.00 | 0.005 | 153.01 |
| 29 | UC44 | 20/03/2012 | 7.50 | NS | 1.20 | 0.010 | 136.26 |
| 30 | UC44 | 25/04/1989 | 6.90 | NS | 1.34 | 0.010 | 172.42 |
ND: No disponible
Modelos analizados
En esta sección se presentan los modelos utilizados para obtener los coeficientes de desplazamiento que se propusieron para esta metodología. Se utilizaron modelos de 1GDL y VGDL, que fueros estudiados (y diseñados) por Moreno (2019).
Los modelos de VGDL son seis marcos rígidos de concreto reforzado en 2D. Se
consideró losa maciza de 15 cm de espesor con comportamiento de diafragma
rígido. Es importante mencionar que para este trabajo se utilizó un porcentaje
de amortiguamiento inherente de todos los marcos de ζ = 2.5%;
mientras que el amortiguamiento suplementario de ζ
ad
= 32.5%. Las columnas se modelaron empotradas a la base. La resistencia
nominal de los materiales de las estructuras fue de
Tabla 2. Elementos y niveles de las estructuras consideradas
| Estructura | Columna | Viga | Número de niveles |
| 1 | C - 1 | T - 1 | 2 |
| 2 | C - 2 | T - 1 | 5 |
| 3 | C - 2 | T - 1 | 10 |
| 4 | C - 3 | T - 1 | 15 |
| 5 | C - 4 | T - 1 | 22 |
| 6 | C - 5 | T - 1 | 30 |
Tabla 3. Propiedades de las secciones de los elementos
| Elemento | Dimensiones, cm | Refuerzo longitudinal | Estribos |
| T - 1 | 30x60 | 8 Var. #6 | #4 @15 cm |
| C - 1 | 45x45 | 8 Var. #6 | #4 @15 cm |
| C - 2 | 55x55 | 12 Var. #6 | #4 @15 cm |
| C - 3 | 70x70 | 12 Var. #8 | #4 @15 cm |
| C - 4 | 75x75 | 12 Var. #8 | #4 @15 cm |
| C - 5 | 85x85 | 16 Var. #8 | #4 @15 cm |
Los periodos y frecuencia de las estructuras calculados con el método de valores característicos se presentan en la Tabla 4. Nótese que estos periodos son los mismos que se consideraron para los osciladores de un grado de libertad.
Tabla 4. Periodos y frecuencias de las estructuras
| Estructura | Pisos | Periodo (s) | Frecuencia (rad/s) |
|---|---|---|---|
| 1 | 2 | 0.40 | 15.71 |
| 2 | 5 | 0.74 | 8.49 |
| 3 | 10 | 1.47 | 4.27 |
| 4 | 15 | 2.02 | 3.11 |
| 5 | 22 | 2.97 | 2.12 |
| 6 | 30 | 4.08 | 1.54 |
Se calcularon los coeficientes de viscosidad de amortiguadores lineales, C L , para cada una de las estructuras estudiadas usando el método de Chirstopoulus y Filiatrault (2006). Después, con la ayuda de la ecuación (3), se obtuvieron los coeficientes de viscosidad de amortiguadores viscosos no lineales, C NL . Éstos se presentan en las Tablas 3 y 4. Los detalles de los cálculos se presentan en Álvarez (2020). Es importante aclarar que en este artículo se incluye, en la parte final, un ejemplo de diseño de una estructura equipada con disipadores en donde se presenta el detalle del diseño de los dispositivos y sus propiedades.
Los modelos estudiados de varios grados de libertad fueron sometidos a los movimientos sísmicos de la Tabla 1 para calcular los desplazamientos máximos en su azotea.
Posteriormente, se analizaron seis modelos de 1GDL con periodos de vibración de 0.4, 0.74, 1.47, 2.02, 2.97, y 4.08 s. Se utilizaron periodos y un amortiguamiento igual al de las estructuras de VGDL anteriormente mencionadas para los osciladores de 1GDL equivalente. La respuesta de los modelos de 1GDL fue evaluada para cada uno de los sismos de la Tabla 1 con ayuda del programa PRISM (2012). Se consideró una respuesta elástica lineal de los osciladores. Se obtuvo el desplazamiento máximo de cada movimiento sísmico para los diferentes periodos de vibración. Los resultados se presentan más adelante junto con desplazamientos de estructuras de varios grados de libertad.
Resultados de los análisis dinámicos
En la Figura 5 se presentan el desplazamiento máximo en la azotea calculado de los marcos equipados con amortiguadores viscosos lineales. Se aclara que se consideró comportamiento lineal de los amortiguadores y de los elementos estructurales. También, se presentan aquellos correspondientes a los osciladores de un grado de libertad. Se puede apreciar que, consistentemente, los desplazamientos de las estructuras de VGDL son mayores a aquellos de los osciladores de 1GDL. Esta relación se discute más adelante y se refiere como coeficiente de desplazamiento, r 1.
Tabla 5. Valores de los coeficientes de viscosidad para las estructuras 1, 2 y 3
| Constantes de viscosidad (t*(s/m) α ) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NIVEL | Estructura 1 | Estructura 2 | Estructura 3 | |||||||||
| Cʟ | Cɴʟ | Cʟ | Cɴʟ | Cʟ | Cɴʟ | |||||||
| α = 1 | α = 0.5 | α = 0.2 | α = 0.05 | α = 1 | α = 0.5 | α = 0.2 | α = 0.05 | α = 1 | α = 0.5 | α = 0.2 | α = 0.05 | |
| 1 | 110.21 | 28.3 | 12.3 | 8.1 | 340.2 | 83.2 | 35.3 | 22.9 | 630.31 | 177.2 | 81.7 | 55.2 |
| 2 | 115.53 | 20.4 | 7.1 | 4.2 | 289.69 | 66 | 26.8 | 17 | 594.38 | 164 | 74.8 | 50.3 |
| 3 | 251.84 | 51.3 | 19.5 | 12 | 568.4 | 152.7 | 68.5 | 45.7 | ||||
| 4 | 227.89 | 38.7 | 13.2 | 7.7 | 555.91 | 142.6 | 62.3 | 41 | ||||
| 5 | 189.06 | 24.5 | 7.1 | 3.8 | 546.37 | 132.1 | 55.7 | 36 | ||||
| 6 | 535.8 | 120.4 | 48.5 | 30.7 | ||||||||
| 7 | 522.47 | 107 | 40.8 | 25.1 | ||||||||
| 8 | 502.49 | 91.3 | 32.4 | 19.2 | ||||||||
| 9 | 464.31 | 71.9 | 23.2 | 13.1 | ||||||||
| 10 | 357.74 | 44.5 | 12.6 | 6.7 | ||||||||
Tabla 6. Valores de los coeficientes de viscosidad para las estructuras 4, 5 y 6
| Constantes de viscosidad (t*(s/m) α ) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NIVEL | Estructura 4 | Estructura 5 | Estructura 6 | |||||||||
| Cʟ | Cɴʟ | Cʟ | Cɴʟ | Cʟ | Cɴʟ | |||||||
| α = 1 | α = 0.5 | α = 0.2 | α = 0.05 | α = 1 | α = 0.5 | α = 0.2 | α = 0.05 | α = 1 | α = 0.5 | α = 0.2 | α = 0.05 | |
| 1 | 2540.8 | 609.7 | 255.7 | 164.8 | 4492 | 760.1 | 258.6 | 150.1 | 8266.4 | 846.5 | 213 | 106.4 |
| 2 | 1994.6 | 523.6 | 231.8 | 153.5 | 3345.9 | 643.4 | 236.3 | 142.5 | 5695.8 | 693.9 | 193.8 | 101.9 |
| 3 | 1806 | 486.6 | 218.8 | 146.1 | 2956.7 | 599.3 | 227.1 | 139.2 | 4795 | 632.2 | 185.1 | 99.7 |
| 4 | 1735.6 | 464 | 207.7 | 138.3 | 2806.9 | 577.9 | 221.1 | 136.1 | 4429.1 | 604.3 | 180.7 | 98.3 |
| 5 | 1703.4 | 445.9 | 197 | 130.4 | 2736.8 | 564.8 | 216.4 | 133.3 | 4250.6 | 588.8 | 177.6 | 97.1 |
| 6 | 1684.6 | 428.3 | 186 | 122 | 2696.4 | 554 | 211.7 | 130.3 | 4150.4 | 578.4 | 175.1 | 95.9 |
| 7 | 1668.5 | 408.8 | 173.6 | 112.6 | 2667 | 542.9 | 206.3 | 126.6 | 4085.6 | 570.4 | 172.9 | 94.7 |
| 8 | 1653.4 | 387.3 | 160.1 | 102.5 | 2641.9 | 530.8 | 200.2 | 122.4 | 4037.2 | 563.4 | 170.7 | 93.5 |
| 9 | 1636.1 | 363.8 | 145.8 | 91.9 | 2617.5 | 517.7 | 193.4 | 117.6 | 3996.5 | 555.6 | 168 | 91.9 |
| 10 | 1614.9 | 337.7 | 130.4 | 80.7 | 2592.8 | 503.8 | 186.2 | 112.6 | 3959.2 | 547.2 | 164.8 | 90 |
| 11 | 1587.5 | 307.8 | 113.6 | 68.7 | 2566.6 | 488 | 178 | 107 | 3923.1 | 539.5 | 162 | 88.4 |
| 12 | 1547.3 | 273 | 95.2 | 56 | 2538.1 | 469.9 | 168.7 | 100.6 | 3887 | 530.7 | 158.7 | 86.4 |
| 13 | 1480.3 | 232.3 | 75.5 | 42.9 | 2506.4 | 450.5 | 158.9 | 93.9 | 3850.1 | 521 | 155 | 84.1 |
| 14 | 1338 | 181 | 53.9 | 29.2 | 2470.7 | 429.9 | 148.7 | 87.1 | 3811.9 | 509.8 | 150.6 | 81.5 |
| 15 | 945.4 | 106.7 | 28.5 | 14.6 | 2428.1 | 406.1 | 137.2 | 79.4 | 3771.8 | 498.6 | 146.2 | 78.8 |
| 16 | 2377.8 | 379.6 | 124.7 | 71.1 | 3729.3 | 486.9 | 141.8 | 76.1 | ||||
| 17 | 2313.9 | 350.3 | 111.4 | 62.6 | 3683.7 | 473.8 | 136.7 | 73.1 | ||||
| 18 | 2231.9 | 317.6 | 97.4 | 53.7 | 3634.2 | 458 | 130.6 | 69.4 | ||||
| 19 | 2113.9 | 278.9 | 81.7 | 44 | 3579.8 | 442.9 | 124.9 | 66 | ||||
| 20 | 1935.5 | 232.6 | 64.5 | 33.8 | 3519.1 | 426.5 | 118.8 | 62.4 | ||||
| 21 | 1630.6 | 175.4 | 45.5 | 23 | 3450.4 | 407.7 | 111.8 | 58.3 | ||||
| 22 | 1024.7 | 97.7 | 23.5 | 11.5 | 3371.4 | 386.3 | 104 | 53.7 | ||||
| 23 | 3278.7 | 364.3 | 96.3 | 49.3 | ||||||||
| 24 | 3167.3 | 340.3 | 88.1 | 44.6 | ||||||||
| 25 | 3029.6 | 312.4 | 79 | 39.5 | ||||||||
| 26 | 2853.4 | 279.8 | 68.6 | 33.8 | ||||||||
| 27 | 2617.6 | 242.5 | 57.5 | 27.8 | ||||||||
| 28 | 2284.9 | 198.5 | 45.3 | 21.5 | ||||||||
| 29 | 1786.8 | 144.3 | 31.5 | 14.6 | ||||||||
| 30 | 1030.2 | 77.2 | 16.1 | 7.3 | ||||||||
Por su parte, en la Figura 6 se muestra, para cada movimiento sísmico, el desplazamiento máximo de azotea de las estructuras de VGDL estudiadas para diferentes valores de exponente de velocidad, α. Se puede apreciar que, mientras para ciertas estructuras los desplazamientos son muy similares, para otras son muy diferentes. Claramente se aprecia que no hay una tendencia simple entre α y los desplazamientos máximos de azotea, pues para algunas estructuras, los desplazamientos crecen con α y para otras, no necesariamente. La relación entre estos desplazamientos y aquellos con α = 1 se analizan más adelante y se refiere como coeficiente de desplazamiento, r 2.
Coeficientes propuestos
Coeficiente r 1
La Figura 7 muestra los coeficientes de
desplazamiento
La ecuación (5) se propone para
calcular el coeficiente
donde N es el número de pisos.
Coeficiente r 2
La Figura 8 muestra ahora los
coeficientes de desplazamiento
Tabla 7. Valores de las constantes
| α | a | b | c | d | f |
|---|---|---|---|---|---|
| 0.5 | 0.71 | 6.49 | 1.22 | 0.82 | 4.19 |
| 0.2 | 0.72 | 13.29 | 2.43 | 1.66 | 9.74 |
| 0.05 | 0.68 | 16.16 | 3.67 | 2.13 | 11.32 |
La ecuación (6) se grafica en
la Figura 9 para los diferentes valores
de
Algunos efectos de interés
Efecto de la rigidez de la conexión entre los amortiguadores y la estructura
Los disipadores viscosos son dispositivos normalmente pequeños que se conectan a las estructuras por medio de brazos metálicos y placas de conexión. En este artículo se le llama conexión al brazo y placas que permiten la transferencia de carga entre el disipador y la estructura. Algunos autores, como Akcelyan et al. (2016), han hecho notar que la rigidez, o la flexibilidad, de la conexión puede tener efectos significativos en la respuesta sísmica de las estructuras. A manera de ejemplo, la Figura 10 muestra la historia de desplazamientos de un marco en 2D (de una crujía y un nivel) sometido el registro sísmico de la SCT, componente Este-Oeste, del sismo del 19/sep/1985. Se consideró respuesta elástica en el marco y periodos de vibración de 0.5 y 1 s. Mientras que la crujía tenía 6 m de ancho, la altura total de la estructura fue de 3 m. El marco se equipó con un disipador viscoso no lineal con exponente de velocidad α= 0.5. El amortiguamiento total del sistema fue de 35%, de los cuales 32.5% lo aportaba el amortiguador y 2.5% el marco. El coeficiente de viscosidad, C NL , se calculó según las ecuaciones (3) a (4). En la figura se muestran los desplazamientos en el marco y las curvas de histéresis (curvas fuerza-deformación) del disipador, empleando conexión infinitamente rígida y conexión flexible (ésta última representada por la línea negra). La conexión flexible se utilizó como un contraventeo convencional con capacidad de carga de 1.2 veces la fuerza máxima transferida por el amortiguador y un factor de esbeltez de (= 1. Se aprecia que la respuesta pico, en términos de desplazamientos laterales, no fue significativamente afectada por la flexibilidad de la conexión, pues las diferencias son menores al 10%. Sin embargo, la forma de las curvas de histéresis del disipador tuvo un cambio drástico; especialmente, para el periodo de 0.5 s. Aunque si se analizan los picos de las curvas de histéresis, los valores de fuerza y desplazamiento máximos son comparables hasta cierto punto.
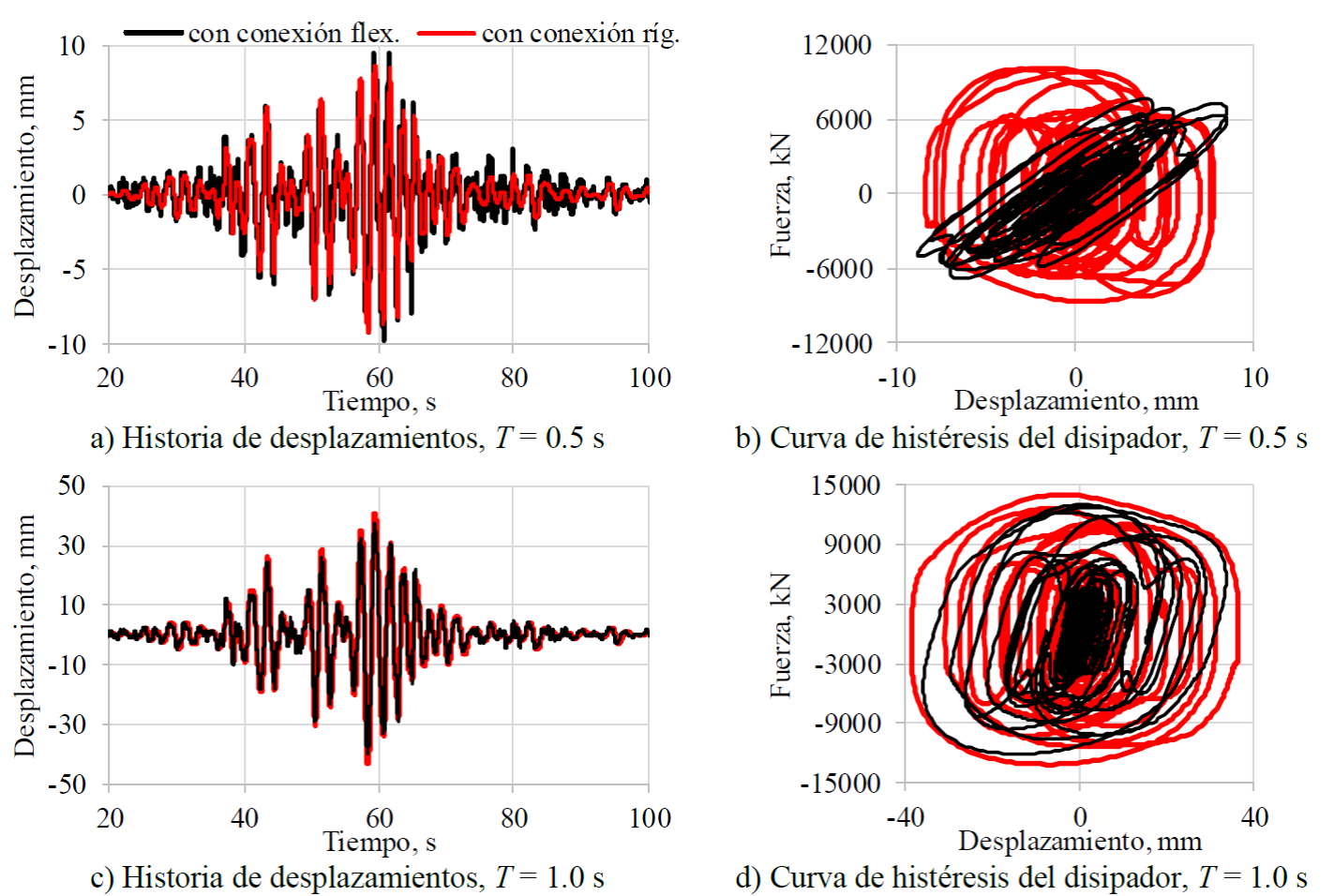
Figura 10. Respuesta sísmica de un marco plano equipado con amortiguador viscoso no lineal ante el movimiento SCT-EO de la estación SCT del 19/sep/1985.
Con la finalidad de comprender mejor la afectación de la rigidez, o flexibilidad, de la conexión en la respuesta sísmica de las estructuras, se calcularon espectros de desplazamientos considerando conexión infinitamente rígida y flexible. Se emplearon diferentes niveles de flexibilidad de la conexión, éstos fueron contraventeos (CV) con capacidad de carga de 1.2, 2, 5 y 10 veces la demanda de fuerza máxima en el disipador cuando se calculó con conexión infinitamente rígida. Se utilizó un factor de esbeltez de (= 1 y una contribución del 32.5% del disipador al amortiguamiento, más 2.5% de la estructura. Los espectros se estimaron para dos tipos de movimientos sísmicos diferentes: la componente Este-Oeste de la estación SCT del sismo del 19/sep/1985 (en suelo blando) y la componente Norte-Sur de la estación NILT del sismo del 7/sep/2017 (en roca). Por conveniencia, las ordenadas espectrales de los casos de conexiones flexibles fueron divididas entre aquellas con conexión infinitamente rígida. Los resultados se muestran en la Figura 11. Se puede observar que existen diferencias entre las relaciones que se obtuvieron con el movimiento de suelo blando y el de roca. Mientras que los valores para el movimiento de suelo blando son cercanos a la unidad (con diferencias < 10%) para periodos mayores a 0.5 s, para el movimiento de roca sólo ocurre en periodos mayores a 1.5 s. Es importante aclarar que las tendencias de la Figura 11 son particulares del exponente α considerado y de los movimientos sísmicos utilizados, por lo que siempre se debe tomar en cuenta, de manera explícita, el efecto de la rigidez (o flexibilidad) del brazo metálico y placas de conexión en la evaluación de la respuesta sísmica de las estructuras y, en caso de que se identifiquen diferencias significativas, hacer los ajustes necesarios para tener un buen comportamiento.
Efecto del tipo de comportamiento estructural del edificio
Autores como Miranda (1999) y Georgoussis (2006) han demostrado que las estructuras a base de marcos presentan comportamiento global en cortante y flexión. Mientras que en marcos de mediana y baja altura predomina el comportamiento global en cortante, en estructuras más altas predomina el comportamiento global en flexión. Esto se debe a que en estructuras de varios niveles la deformación axial de las columnas tiende a incrementar, lo que se refleja en un comportamiento global flexión (Ezeh e Ibearugbulem, 2009). Se considera que las estructuras tienen un comportamiento global en cortante cuando el perfil de desplazamientos, producido por fuerzas laterales, muestra una forma de doble curvatura (Figura 12a). Por otro lado, cuando el perfil de desplazamientos muestra una curvatura simple, se presenta un comportamiento global en flexión, como se muestra en la Figura 12b. Para el caso de estructuras equipadas con amortiguadores viscosos, el comportamiento global en cortante es preferible, pues la mayoría de la distorsión de entrepiso resulta en deformación axial del dispositivo. En el caso de deformación global en flexión, una buena parte de la distorsión de entrepiso no produce deformación axial en los disipadores.
El tipo de comportamiento global en flexión se debe principalmente a la
deformación axial de las columnas en una estructura. Mientras mayor sea la
deformación axial en las columnas mayor será el comportamiento global a flexión
(Figura 12b). Por su parte, el
comportamiento global en cortante en una estructura equipada con amortiguadores
viscosos no lineales es preferible ya que permite a los dispositivos deformarse
axialmente y, por ende, disipar energía, dándole a la estructura una mejor
respuesta. Esto ocurre porque en un comportamiento global en cortante se
presenta una mayor deformación axial de los amortiguadores. En cambio, para un
comportamiento global en flexión las deformaciones son menores. Ello se puede
apreciar esquemáticamente en la Figura 13
de un marco simple modelado en el programa ETABS
(2017), donde, considerando una misma deformación lateral,
D
x
, la deformación global en cortante genera deformaciones mayores en los
amortiguadores que para el caso de deformación global en flexión. Para comprobar
eso de manera gráfica, primero véase en la Figura
13b que las columnas se deforman axialmente de tal manera que las
columnas del lado izquierdo se alargan, mientras que las del lado derecho se
acortan, produciendo una deformación global en flexión. Después, arbitrariamente
se extraen los amortiguadores del segundo nivel de cada marco para medir la
deformación axial generada por una carga lateral. Claramente se puede observar
que la deformación axial en el disipador del marco izquierdo,
Con la finalidad de analizar los efectos del comportamiento global en flexión en
las distorsiones de entrepiso de una estructura, se presenta un ejemplo de un
marco en 2D de acero de 12 niveles y una crujía, equipada con amortiguadores
viscosos no lineales. La estructura se modeló empotrada en la base y con
diafragmas rígidos en los entrepisos. Se calculó un periodo fundamental de 1.86
segundos en el programa ETABS (2017).
Para los amortiguadores, se consideró un exponente de velocidad
donde
La estructura del ejemplo se evaluó usando análisis dinámico tipo paso a paso
para diferentes valores de
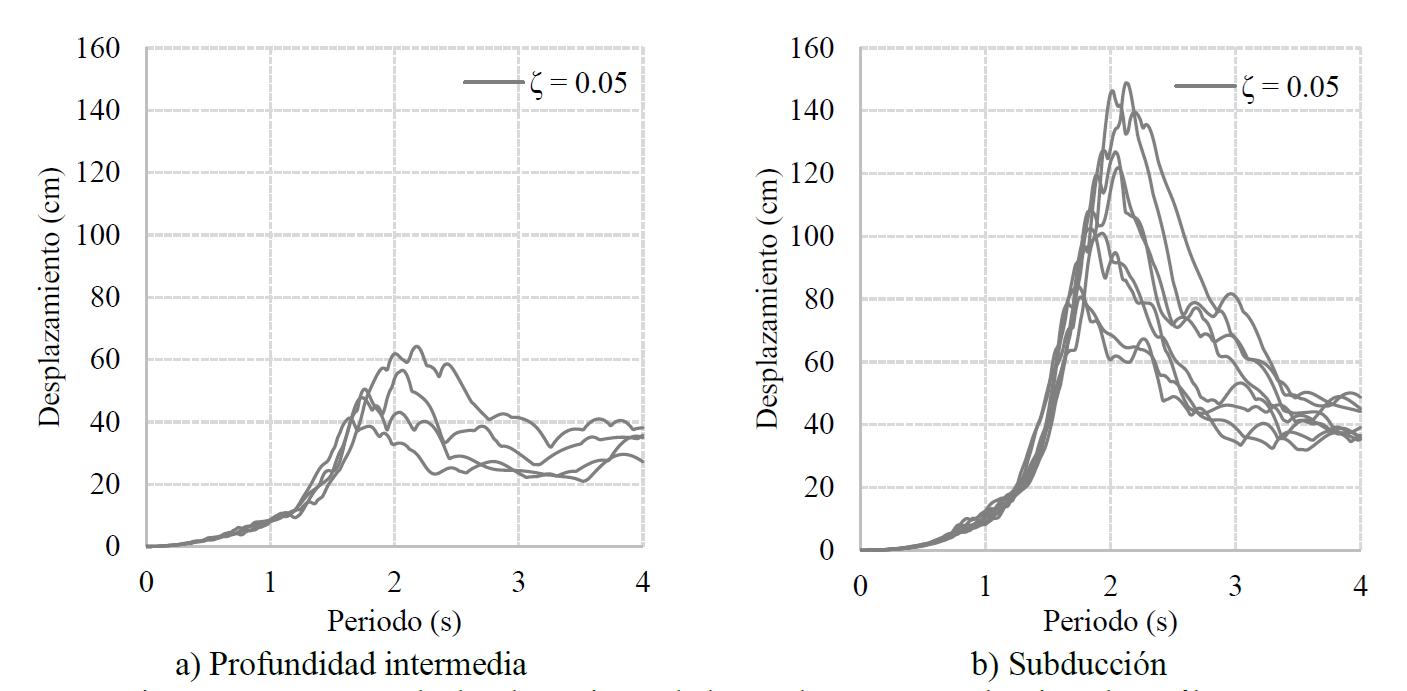
Figura 18. Espectros de desplazamiento de los acelerogramas seleccionados (sólo se muestran aquellos de la componente h1).
Por otro lado, se obtuvo la distorsión de entrepiso máxima en la altura del
marco, se normalizó contra aquella que corresponde a
donde la constante
Nótese que los cálculos realizados en esta sección corresponden a una estructura de acero de 12 niveles en 2D, equipada con amortiguadores viscosos no lineales con α= 0.5. Los resultados se deben interpretar para esas características particulares y considerar que las constantes a y b de la ecuación (8) propuesta podrían variar si los parámetros cambian. Ciertamente, más análisis deben ser realizados para encontrar tendencias centrales.
Metodologías de diseño
En la literatura existen algunas metodologías de diseño de estructuras equipadas con amortiguadores viscosos. Alotta et al. (2016) propusieron un procedimiento simplificado basado principalmente en la definición de un amortiguamiento adicional objetivo para después obtener coeficientes de viscosidad en cada nivel de la estructura. Palermo et al. (2018) desarrollaron una metodología de cinco pasos que considera principalmente un parámetro objetivo, como la distorsión, ecuaciones simples para obtener los coeficientes de viscosidad de los amortiguadores y sus características y, además, el diseño preliminar de los elementos estructurales a partir de análisis estáticos equivalentes. Pekcan et al. (1999) emplearon, en el diseño de los amortiguadores viscosos y de las estructuras equipadas con ellos, la velocidad efectiva en vez de la pseudo-velocidad debido a las diferencias que puede haber entre ellas y, en consecuencia, en las propiedades de los amortiguadores. Dong et al. (2016) realizaron una evaluación de marcos de acero equipados con amortiguadores utilizando el documento ASCE-7-10 (2010), para diferentes niveles de fuerza cortante basal, yendo por debajo del porcentaje límite establecido para una estructura equipada con amortiguadores viscosos. En México, el grupo de trabajo de la Dra. Ruiz y colaboradores (Ruiz, 2018) han realizado estudios sobre el comportamiento de estructuras con amortiguamiento viscoso, estos estudios se han incorporado a las normas de diseño.
Después de una revisión bibliográfica detallada, se observó que las metodologías de diseño actuales, disponibles en la literatura cuentan con características específicas para el diseño de estructuras con amortiguadores viscosos. Esas metodologías varían desde procedimientos simplificados o ecuaciones simples, hasta procedimientos complejos y difíciles de implementar. Sin embargo, estos autores consideran que aún falta una metodología que sea aplicable para las condiciones de suelo blando de la Ciudad de México y que incluya efectos como la deformación axial del brazo de conexión de los dispositivos a la estructura, así como los efectos de la deformación axial de las columnas del sistema de marcos. Por esas razones, a continuación, se propone una metodología simplificada para el diseño de estructuras con amortiguadores viscosos empleando osciladores de 1GDL equivalentes y coeficientes de desplazamiento, aplicable a las condiciones de suelo blando de la Ciudad de México.
Método de diseño propuesto
Se propone un método de diseño de estructuras equipadas con amortiguadores viscosos no lineales. El método considera estimar, de manera simple, los desplazamientos de estructuras equipadas con amortiguadores viscosos no lineales con ayuda de un modelo equivalente de 1GDL y dos coeficientes de desplazamiento. Primero, se propone la ecuación (9), que permite estimar el desplazamiento máximo en la azotea de una estructura de VGDL equipada con amortiguadores viscosos no lineales:
donde
El método consiste principalmente en once pasos que se muestran en el diagrama de flujo de la Figura 16 y se explican a continuación:
Paso 1. Proponer un diseño preliminar de la estructura primaria. Se le llama estructura primaria al sistema de marcos. Se recomienda iniciar con un diseño por cargas gravitacionales (cargas muertas y vivas), considerando las recomendaciones de las NTC (2017). En pasos posteriores se verificará si el diseño por cargas gravitacionales es suficiente o se requerirá un incremento de la capacidad.
Paso 2. Seleccionar una distorsión de entrepiso máxima, γ máx . Se recomienda un valor de 0.01 ya que estudios numéricos y experimentales como Guerrero et al. (2018) muestran que estructuras a base de marcos comienzan a fluir a distorsiones de entrepiso cercanas a 0.01. Ciertamente, algunos marcos podrían fluir a distorsiones ligeramente menores a ese valor, pero su comportamiento no lineal sería menor, por lo que no existiría daño estructural de preocupación en la edificación. Esto resulta significativo ya que los objetivos de los amortiguadores es proteger a las estructuras. En ese sentido conviene establecer un límite distorsión de entrepiso bajo, como el que aquí se recomienda, con el fin de evitar daño significativo en los marcos del sistema estructural.
Paso 3. Obtener espectros de desplazamiento para diferentes niveles de amortiguamiento. Los espectros de desplazamiento se pueden obtener de varias fuentes. Sin embargo, se recomienda calcularlos a partir de acelerogramas reales o sintéticos. En el caso de la Ciudad de México, el programa SASID (2020) provee acelerogramas sintéticos para cualquier ubicación dentro de la ciudad. Con esos acelerogramas se pueden obtener promedios de espectros de desplazamiento para diferentes niveles de amortiguamiento lineal.
Paso 4. Estimar el periodo fundamental de vibración de la estructura y el periodo dominante del suelo. El primero se puede estimar con un modelo tridimensional en un programa de análisis comercial. El segundo se puede determinar con vibración ambiental o con alguna metodología reconocida. En algunas ciudades, como la Ciudad de México, éste se puede calcular siguiendo recomendaciones reglamentarias o de programas como SASID (2020).
Paso 5. Calcular el desplazamiento máximo permitido para un oscilador equivalente de un grado de libertad. Para ello, primero se estima el desplazamiento en la azotea, D az , que de acuerdo con Terán y Virto (2009), se puede calcular como:
donde H es la altura del edificio y
donde
Entonces, las ecuaciones (9) a (11) se reordenan para calcular el desplazamiento máximo permitido en un oscilador equivalente de un grado de libertad, esto es:
donde todas las variables ya han sido definidas. Nótese que los coeficientes r 1 y r 2 dependen del número de niveles, de los periodos obtenidos en el paso 4 y del exponente de velocidad, α, de los amortiguadores. Para este último se recomienda consultar a los proveedores con la finalidad de obtener un valor comercialmente conveniente. Un valor de α = 0.5 se puede tomar de manera preliminar como valor inicial.
Paso 6. Encontrar un nivel de amortiguamiento adecuado. Éste se obtiene a partir de los espectros de desplazamiento del paso 3, el periodo de vibración del paso 4, y el desplazamiento máximo permitido del paso 5. Se ingresa al espectro con el valor del periodo de vibración y con el desplazamiento máximo permitido. El valor del amortiguamiento que permite controlar los desplazamientos laterales es aquel correspondiente al espectro cuyas ordenadas sean menores o iguales al desplazamiento máximo permitido para el periodo de la estructura.
Paso 7. Calcular los coeficientes de viscosidad de amortiguadores viscosos lineales, C L , con algún método conocido, como el método de Christopoulos y Filiatrault (2006) o el método de ASCE 41-17 (2017).
Paso 8. Convertir las constantes de viscosidad, C L , de amortiguadores lineales a aquellas para amortiguadores no lineales, C NL , con la ecuación (3).
Paso 9. Diseñar el brazo conector de los amortiguadores a la estructura. Esto se puede hacer siguiendo recomendaciones como aquellas de las Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Acero versión 2020 (NTCA-2020), para la fuerza axial máxima esperada en los amortiguadores. Otro aspecto importante que se debe revisar es la rigidez del brazo conector. Se recomienda que ésta sea tal que la deformación axial del brazo sea menor (digamos) al 20% de la deformación del disipador ante la carga máxima esperada. Ciertamente se requieren más estudios para validar esta conjetura, pero limitar la deformación del brazo conector al 20% de la deformación del disipador se considera un buen diseño preliminar.
Paso 10. Estimar el valor del factor r (ver ecuación 7) para comprender el nivel de comportamiento global en flexión de la estructura y, en caso de ser necesario, realizar el ajuste correspondiente. Aquí conviene aclarar que, como un primer paso, se puede calcular el incremento de la distorsión de entrepiso con el apoyo de la ecuación (8) y decidir si dicho incremento es significativo o no. En tal caso, se puede optar por incrementar el área axial de las columnas que soportan a los dispositivos para disminuir el valor de r o, como otra opción, incrementar el tamaño de los disipadores. Ciertamente, queda a juicio del diseñador seleccionar la alternativa que más convenga a su proyecto.
Paso 11. Verificar el diseño con análisis dinámico no lineal tipo paso a paso. Si el resultado es satisfactorio, el proceso de diseño termina. De lo contrario, se puede modificar el diseño preliminar de la estructura primaria o flexibilizar el límite de distorsión de entrepiso.
Ejemplo de aplicación
Se presenta un ejemplo de diseño. Se trata de una estructura en 2D de concreto
reforzado de 12 niveles con columnas de 70x70 cm, armadas con 12 varillas del #8 y 3
estribos del #4 separados a cada 15 cm. Las vigas son de 40x60 cm con 4 varillas del
#6 en cada lecho y estribos del #4 a cada 15 cm. Para el modelo se usaron las
siguientes propiedades de materiales: concreto con
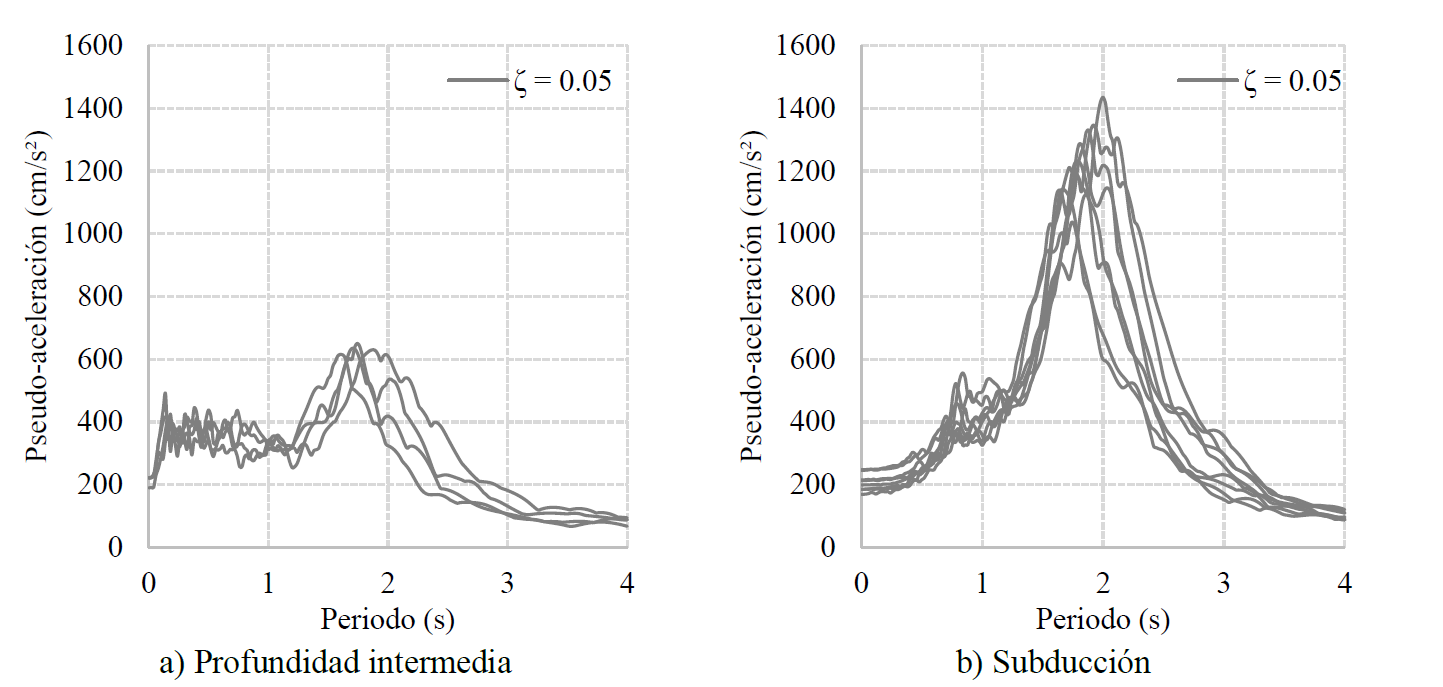
Figura 19. Espectros de pseudo-aceleración de los acelerogramas seleccionados (sólo se muestran aquellos de la componente h1).
Solución
Paso 1. Se realizó un diseño preliminar del marco que culminó con las propiedades descritas en el planteamiento del problema.
Paso 2. Se define una distorsión de entrepiso máxima de γ máx = 0.01.
Paso 3. Se obtienen espectros de desplazamiento promedio para diferentes niveles de amortiguamiento (ver Figura 20). Nótese que se obtuvieron unos espectros para profundidad intermedia y otros para subducción.
Paso 4. El periodo de vibración de la estructura se estimó como 1.66 s en ETABS (2017) y el periodo dominante del suelo según SASID (2020) es de 2 s.
Paso 5. Se calcula el desplazamiento máximo permitido para un
oscilador equivalente de un grado de libertad. Se consideró α =
0.5,
Donde N = 12, T/T g = 0.83, a = 0.71, b = 6.49, c = 1.22, d = 0.82, f = 4.19. Entonces,
Paso 6. Se estima el nivel de amortiguamiento adecuado. De los espectros de desplazamiento de la Figura 20 se aprecia que para el periodo de la estructura rigen aquellos de la zona de subducción ya que presentan ordenadas mayores. De la Figura 20b se observa que para un periodo de 1.66 s el espectro con amortiguamiento de 30% queda por debajo de la demanda de 290 mm, por lo que se elige ese valor como amortiguamiento adecuado.
Paso 7. Se calculan los coeficientes de viscosidad de amortiguadores viscosos lineales con el método del ASCE 41-17 (2017). Para este ejemplo se consideraron dos tipos de amortiguadores viscosos. Esto se debe a que en la práctica profesional suele ser menos costoso proponer un tipo de amortiguador para diferentes niveles que uno para cada nivel. Como ejemplo, uno de los edificios más conocidos en la Ciudad de México, la Torre Mayor cuenta con 98 amortiguadores de sólo dos tipos diferentes (Taylor, 2003). El primer dispositivo propuesto para este ejemplo va del primer nivel al quinto y el segundo del sexto nivel en adelante. Los coeficientes propuestos se muestran en la segunda columna de la Tabla 8. Su cálculo detallado se presenta en el Apéndice A.
Tabla 8. Valores de los coeficientes de viscosidad
| NIVEL | Cʟ, t.s/m | Cɴʟ, t.(s/m) α |
|---|---|---|
| α = 1 | α = 0.5 | |
| 1 | 558.25 | 160 |
| 2 | 558.25 | 160 |
| 3 | 558.25 | 160 |
| 4 | 558.25 | 160 |
| 5 | 558.25 | 160 |
| 6 | 279.13 | 80 |
| 7 | 279.13 | 80 |
| 8 | 279.13 | 80 |
| 9 | 279.13 | 80 |
| 10 | 279.13 | 80 |
| 11 | 279.13 | 80 |
| 12 | 279.13 | 80 |
Paso 8. Se convierten las constantes de viscosidad, C L , de amortiguadores lineales a aquellas para amortiguadores no lineales, C NL , con la ecuación (3). La tercera columna de la Tabla 8 muestra los coeficientes de viscosidad. Su cálculo se muestra a detalle en el Apéndice A.
Paso 9. Diseño del brazo conector de los amortiguadores a la estructura. Éste se diseña para la fuerza máxima del amortiguador, incrementada por un factor de seguridad. La fuerza máxima ocurre en el instante de velocidad máxima. La velocidad máxima se puede obtener de manera aproximada multiplicando el desplazamiento máximo relativo, en los extremos del disipador, por la frecuencia del movimiento de la estructura.
Por simplicidad, y tomando en cuenta inicialmente un comportamiento global en
cortante, se considera que el desplazamiento máximo en el disipador es el
producto de la distorsión de diseño, por la altura de entrepiso, por el coseno
del ángulo, esto es:
Por simplicidad, en esta sección se muestra el diseño del tipo de amortiguador
para los niveles del 1 al 5. A partir del desplazamiento máximo,
La fuerza máxima,
La fuerza de diseño,
Se debe entonces emplear un brazo (o contraventeo) de conexión que tenga una
resistencia mayor o igual a
donde
y
donde r
*
es el radio de giro de la sección del elemento,
que resulta mayor que la fuerza de diseño, por lo que el perfil OC 244 x 4.8 mm se considera adecuado en términos de resistencia. Ahora, en términos de rigidez, ésta resulta:
Nótese que la rigidez del brazo se obtuvo con una longitud actuante que es igual a la longitud efectiva menos 50 cm de longitud de los amortiguadores. Entonces, el desplazamiento esperado en el brazo conector es:
Lo que, en términos del desplazamiento máximo del disipador, es:
valor que resulta menor a 20% establecido como un límite aceptable.
El procedimiento para el diseño del amortiguador para los niveles 6 a 12 es similar al mostrado anteriormente. Se obtuvo que el perfil de acero que cumple por resistencia a compresión para el tipo de amortiguador en los niveles 6 a 12 es el perfil OC 175 x 4.8 mm. Con una resistencia a compresión de 37.94 t. La rigidez calculada se usó para modelar los amortiguadores.
Paso 10. Se estima el valor del factor r para
comprender el nivel de comportamiento global en flexión de la estructura. Para
ello, se obtuvo el periodo de la estructura considerando rigidez infinita en
vigas y amortiguadores, lo que resultó en
dado que el valor de r resultó ser muy bajo, se considera que el comportamiento global en flexión de la estructura es insignificante, por lo que no se debe hacer ninguna corrección en este caso. Para valores de r mayores a 0.05 se recomiendan algunas de las siguientes alternativas: 1) modificar el amortiguamiento proveído por los disipadores, 2) incrementar la rigidez axial de las columnas de soporte de los disipadores para reducir r, 3) aumentar la rigidez de la estructura con la finalidad de tomar en cuenta el incremento de las distorsiones de entrepiso (ver Figura 14) producido por el efecto global en flexión. Ciertamente el diseñador deberá elegir cual es la opción más apropiada para su proyecto.
Paso 11. Se verifica el diseño con análisis dinámico no lineal tipo paso a paso. Con ayuda del programa ETABS (2017), el modelo fue sometido a los movimientos sísmicos seleccionados.
En las Figuras 21 y 22 se muestran los perfiles de desplazamiento y distorsiones de entrepiso del modelo, respectivamente. Se puede observar que el perfil promedio de las distorsiones de entrepiso (líneas continuas) tienen un valor máximo de 0.004 para movimientos de profundidad intermedia y de 0.0102 para movimientos de subducción. Sólo los últimos generaron demandas de distorsión ligeramente superiores al límite establecido en el paso 1 de 0.01. Se puede decir entonces que el diseño es aceptable. Además, en la Figura 23 se muestran, para el caso de los movimientos de subducción, los perfiles promedio de desplazamientos y distorsiones de entrepiso de la estructura con y sin amortiguadores viscosos. Esto se graficó con el fin de comparar y observar el beneficio, en la reducción de la respuesta sísmica, que pueden proporcionar los amortiguadores viscosos. Se puede observar que, para este caso, los amortiguadores viscosos empleados redujeron en un 80% los desplazamientos y las distorsiones de entrepiso, comprobando su efectividad en la reducción de la respuesta sísmica.
Conclusiones
En este artículo se mencionaron las características generales de los amortiguadores viscosos y cómo pueden mejorar la respuesta sísmica de estructuras, reduciendo los desplazamientos y distorsiones, así como las fuerzas que se inducen en el sistema primario.
También se mostró que la respuesta sísmica de estructuras equipadas con amortiguadores viscosos no lineales puede llegar a ser significativamente diferente a aquella con amortiguadores viscosos lineales. Esto es debido a que las propiedades de los amortiguadores no lineales se calculan frecuentemente a partir de las propiedades de amortiguadores lineales usando el enfoque de balance energético, propuesto por Lin y Chopra (2002), el cual no necesariamente conduce a desplazamientos laterales similares. Para corregir el problema, se propuso un método simple para el diseño de estructuras equipadas con amortiguadores viscosos no lineales. El método se basa en usar un modelo equivalente de 1GDL y coeficientes de desplazamiento que toman en cuenta la no linealidad de los amortiguadores y el efecto de varios grados de libertad. El método consta principalmente en 11 pasos generales y se proponen ecuaciones simples para calcular los coeficientes de desplazamiento. Además, en esta metodología se estima el porcentaje de amortiguamiento necesario para cumplir con un límite de distorsión de entrepiso máxima, lo que la hace muy transparente.
También se mostró que existen otros factores que afectan los desplazamientos laterales de las estructuras equipadas con amortiguadores viscosos: 1) la flexibilidad del brazo que conecta el disipador a la estructura, la cual puede modificar de manera importante la respuesta de la estructura, y 2) el comportamiento global en flexión. Para mostrar la aplicación del método propuesto, se diseñó una estructura de 12 niveles equipada con amortiguadores viscosos no lineales. El diseño fue validado con análisis dinámicos no lineales. Se observó que el comportamiento de la estructura fue satisfactorio de acuerdo con los objetivos de diseño planteados. Se concluye que el método de diseño propuesto es apropiado para fines de diseño sísmico.











 nueva página del texto (beta)
nueva página del texto (beta)




















