2.1. Data

This study employs micro-level data from Mexican censuses conducted by the National Institute of Statistics and Geography (Instituto Nacional de Estadística y Geografía, INEGI) in 1990, 1995, 2000, 2010, and 2015; these data are available on the IPUMS International web site (https://international.ipums.org/inter-national). The sample fraction available is 10 percent for 1990, 0.4 percent for 1995, 10.6 percent for 2010, and 9.5 percent for 2015. The universe for all samples is individuals aged 12 and above. Data on earnings from the 1970 census are not comparable to earnings reported in the selected censuses, and the 1980 census microdata is no longer available since it was lost in the 1985 Mexico City earthquake.⁵

The censuses collect data on labor income and earnings for the previous month. These earnings include wage income from businesses, farms, and other sources. One of the main advantages of focusing on earnings is that earnings capacity, such as that represented by skills and effort, is transferred from parents to children differently than other assets. Earnings capacity can be transferred through investment in human capital (^{Becker et al., 2018}), while other assets are transferred directly from parents to children (^{Becker and Tomes, 1986}). In this sense, earnings provide the best proxy for opportunities related to individual merit (^{Mazumder, 2005}).

Mexican censuses do not link individuals across years. We thus follow the synthetic approach of ^{Aaronson and Mazumder (2008)}, which requires a core sample that clearly distinguishes between adult children and synthetic families, allowing us to compare how much adult children’s earnings differ from their synthetic family earnings. We define adult children as men who are 20 years old in the 1995-2015 censuses; these individuals are old enough to report earnings.⁶ Synthetic families are defined as representative family units where adult children are likely to be members, as determined by two variables: the state in which they were born and their birth cohort. The earnings of such representative families are the synthetic family earnings. With these definitions, synthetic families are observed in the 1990, 1995, and 2000 censuses, and adult children are observed in those of 1995, 2000, 2010, and 2015. For example, a 30-year-old man born in Mexico City who reports earnings in the 2010 census is virtually matched with a Mexico City family reporting earnings in the 1990 census, whose children were approximately 10 years old at that time. For the purposes of this study, we consider four birth cohorts: 1971-75, 1976-80, 1981-85, and 1986-90. We take the state where they were born, as reported in the censuses; since there are 32 states, the number of representative families is 128.

Once we have defined the core sample and the linkage between individuals and families across censuses, we compute synthetic family earnings. First, for the 1990-2000 censuses, we assign cohorts to children born in Mexico. During this time, children live with their parents; hence, by assigning a birth-cohort we are identifying potential families of future generations. This task is conditional on the available information. For instance, in the 1990 census, we can identify individuals from all birth cohorts, as shown in table 1, column (1); in other words, all men born between 1971 and 1990 are children in the 1990 census. Column (2) shows their age. However, for the 1995 and 2000 censuses we can only assign the 1981-85 and 1986-90 birth cohorts, since individuals born in prior cohorts have become adult children by the time of those censuses, as shown in column (4). By the time of the 2010 and 2015 censuses, all of the children have become adults and no families are observed.

Once children are assigned to a birth cohort, we add the earnings of household heads and spouses to compute parental earnings in each census year. We also assign these earnings to children. In the case of families with children belonging to different cohorts or who were born in different states, the same parental earnings are assigned to each one. We assign family earnings regardless of other family characteristics (such as family size, children’s gender, or parents’ marital status). As a final step, we compute synthetic family earnings (SFE). These are the average parental earnings assigned to children i that were born in state s, where c = {1, ..., 32}; in birth cohort c, where c = {1971 − 75, 1976 − 80, 1981 − 85, 1986 − 90}; observed in census year t, where t = {1990, 1995, 2000, 2010}. This can be written as follows:

This definition allows us to compute family earnings for the same cohort at different points in time. For example, in table 1, column (1), we can observe that for the birth cohort 1981-85 it is possible to estimate the SFE in 1990, 1995, and 2000. In such cases, we calculate the period average to smooth cyclical variation in the family’s earnings (^{Mazumder, 2005}). This results in an SFE for each birth cohort and state of birth. Table 1, column (3) shows the SFE for each cohort. These earnings turn out to be very similar for the 1971-75, 1976-80 and 1981-85 birth cohorts, just above MXN 5,600 per month, while for the 1986-90 birth cohort the SFE is around MXN 5,800 per month. Column (6) shows the mean of adult children’s monthly earnings, including those individuals reporting zero earnings. This amount ranges from MXN 2,795 to MXN 6,381. Column (7) reports the number of observations per cohort in every census. The total sample has approximately 2.6 million observations.

2.1. Empirical strategy

The empirical strategy follows the existing literature for estimating intergenerational economic persistence by allowing for time-varying estimates (e.g., ^{Aaronson and Mazumder, 2008}; ^{Lee and Solon, 2009}). The basic specification can be written as follows:

where log⁡GCEi,c,s,t is the log of monthly earnings (in 2010 MXN) for a grown child i, belonging to birth cohort c, born in state s, reporting earnings in census year t. The key independent variable is log⁡SFEc,s which indicates a multi-year average, for some cohorts, of monthly synthetic earnings of families whose children were born in cohort c and state s.⁷ The specification also includes the log of family earnings interacting with census years and birth cohort to measure intergenerational mobility over time. Although a large body of the literature has focused on fathers’ earnings (see ^{Solon 1999}), we use family earnings, since these provide a broader measure of the family resources for children’s opportunities (^{Chadwick and Solon, 2002}; ^{Mazumder, 2005}; ^{Mayer and Loopo, 2005}).⁸

The coefficients of interest are β,ρt , ρt and δc Since both adult children’s earnings and family earnings are expressed in logarithmic form, these coefficients are the intergenerational income elasticity.⁹ They provide different descriptive measures of IGE depending on the restrictions set into the specification. If we set ρt= and δc=0 , the resulting estimate β is the time-invariant IGE estimate, and it refers to a descriptive measure of economic mobility at the national level. If δc=0 and β=0 , the resulting estimates ρt are time-variant, allowing the IGE to vary across census years: this is a time-trend IGE. Changes in the IGE time trend may reflect changes in childhood investment over time in line with changes in returns to skills. If ρt=0 and β=0 , the resulting estimates δc are cohort-variant, allowing the IGE to vary across cohorts. ¹⁰ This trend is likely to capture changes if cohorts were exposed to different policies (^{Nybom and Stuhler, 2013}).¹¹ For example, younger cohorts in Mexico were eligible for social policy programs that broadened their access to higher education, so these individuals were likely to show higher intergenerational mobility than those in older cohorts. If there are no restrictions, it is possible to estimate a general intergenerational economic mobility trend. In this case, we combine both census year and cohort effects.¹²

Specification (2) also accounts for additional factors that, according to the literature, could bias the results. The vector Xi,c,s,t controls for age profile and heterogenous age-earnings profiles to reduce plausible biases (^{Lee and Solon, 2009}). It includes a quadratic polynomial for individuals’ age centered at 40 (^{Altonji and Williams, 2005}; ^{Haider and Solon, 2006}) and its interaction with family earnings (^{Böhlmark and Lindquist, 2006}; ^{Lee and Solon, 2009}).¹³ Additionally, πr , γr and ϕr are cohort, year, and birth region fixed effects. Cohort fixed effects control for time-invariant characteristics across cohorts, while census year fixed effects capture global trends that affect all individuals similarly. We also consider four birth regions, so that ϕr controls for time-invariant factors that could determine intergenerational mobility at the time of birth.

Specification (2) is similar to one employing state of birth and birth cohorts as instrumental variables (^{Aaronson and Mazumder, 2008}). If these variables exogenously determine family earnings from previous generations, it is possible for the OLS estimate for β to be consistent. In this sense, our estimate is similar to a two-sample instrumental variable estimator (^{Klevmarken, 1982}; ^{Angrist and Krueger, 1992}). One issue with our estimates is the presence of nonobservable characteristics that are correlated with synthetic family earnings. However, if the direction of the bias and its magnitude is constant over time, the bias should not affect the general pattern reflected in our estimates (^{Aaronson and Mazumder, 2008}).¹⁴

One concern is that specification (2) does not allow us to analyze the importance of birthplace in determining adult children’s outcomes. Since part of the exogenous source of variation in synthetic family earnings is the state of birth, that variation is lost in the analysis of intergenerational mobility across states of birth. However, we overcome this problem by allowing synthetic family earnings to vary across regions of birth. We consider the four regions defined by the Mexican central bank (^{Banco de México, 2016}): north (Baja California, Sonora, Chihuahua, Coahuila, Nuevo León, and Tamaulipas), north-center (Sinaloa, Durango, Zacatecas, San Luis Potosí, Nayarit, Tlaxcala, Aguascalientes, Jalisco, Colima, and Michoacán), center (Mexico City, Estado de México, Morelos, Puebla, Tlaxcala, Hidalgo, Querétaro, and Guanajuato), and south (Guerrero, Oaxaca, Chiapas, Veracruz, Tabasco, Campeche, Yucatán, and Quintana Roo). Since each of these regions contains several states, it is possible to rely on some variation to compute IGE estimates by region of birth. For this task, we use the following specification:

Specification (3) estimates the time-invariant IGE for each birth region, and πr captures the place-based factors determining family background when individuals were children, such as public investment within a region, or policies that enhanced human capital, like child care systems or scholarship programs. The specification also includes cohort fixed effects, census-year fixed effects, and life-cycle controls. It is important to mention that these estimates are merely qualitative, given the limited data.

A second concern is the cross-country comparability of our timeinvariant IGE estimate, which is crucial to understanding the underlying factors driving intergenerational economic mobility (^{Corak, 2016}; ^{Solon, 2004}). To address this problem, we follow the framework proposed by ^{Corak (2006)} for cross-country comparison. Employing this framework, the author uses metadata from the literature to select representative estimates for several countries and scale them by a factor that considers the U.S. as a reference and a U.S. estimate that would adjust for the difference in sample characteristics and methodologies across countries.¹⁵ The scaling factor is defined as follows:

where β* is our preferred estimate. βan is the U.S. estimate of reference, and βsa is the estimate adjusted for sample characteristics and methodologies.

3.1 Time-invariant and time-variant IGE estimates

Table 2 presents time-invariant IGE estimates at the national level, in which ρt=0 and δc=0 . All coefficients are positive and statistically significant at the 1 percent level. Column (1) shows the IGE estimate with no controls, and column (2) adds cohort and year fixed effects. Column (3) shows the results for a quadratic polynomial for age, and column (4) those for the polynomial with each term interacting with family earnings. Column (5) presents the IGE estimate with region of birth fixed effects. Column (6) presents the IGE estimate considering all of the controls specified in equation (2). With no controls the estimate suggests that a 1 percent increase in family earnings is associated with an increase of 0.45 percent increase in adult children’s earnings. Columns (2) and (3) suggest that the estimate is barely modified when including fixed effects and the age earnings are measured. Columns (4) and (5), which incorporate all life-cycle controls, suggests that the absence of such controls does bias the estimates downwards. Finally, column (6) shows that the IGE estimates decrease by 6.4 percent with respect to those shown in column (5).

A first benchmark for comparison is the baseline IGE estimate for the U.S. reported in ^{Aaronson and Mazumder (2008)}, which is 0.43. If we consider the main estimate in column (5) to have the most similar specification and sample characteristics, persistence is greater in Mexico. A second benchmark uses the intergenerational income elasticities reported by ^{Rojas-Valdés (2012)}, and it varies significantly, depending on the type of estimate and sample characteristics. For his two-sample instrumental variable estimate, the IGE is about 0.31, which is 36 percent lower than the estimate in column (5), while his estimate for a pseudo-panel sample yields a value of 0.6, which is 20 percent higher than our estimate.

One concern here is the extent to which our IGE time-invariant estimates are robust to sampling changes. There are four alternative samples of interest: 1) families whose children belong to the same birth cohort (^{Aaronson and Mazumder, 2008}), 2) adult children aged 25 or older (e.g., ^{Solon, 1992}), 3) adult children aged 30 or older (e.g., ^{Mazumder, 2001}), and 4) synthetic families with parents aged 40-50 and children 30 or older (e.g., ^{Zimmerman, 1992}). Following specification (2) and the appropriate restriction to estimate the IGE, figure 1, panel A shows the resulting OLS estimates for this robustness check, with the estimates indicated by blue squares with 95 percent confidence intervals. The estimates are similar for most of the sample.

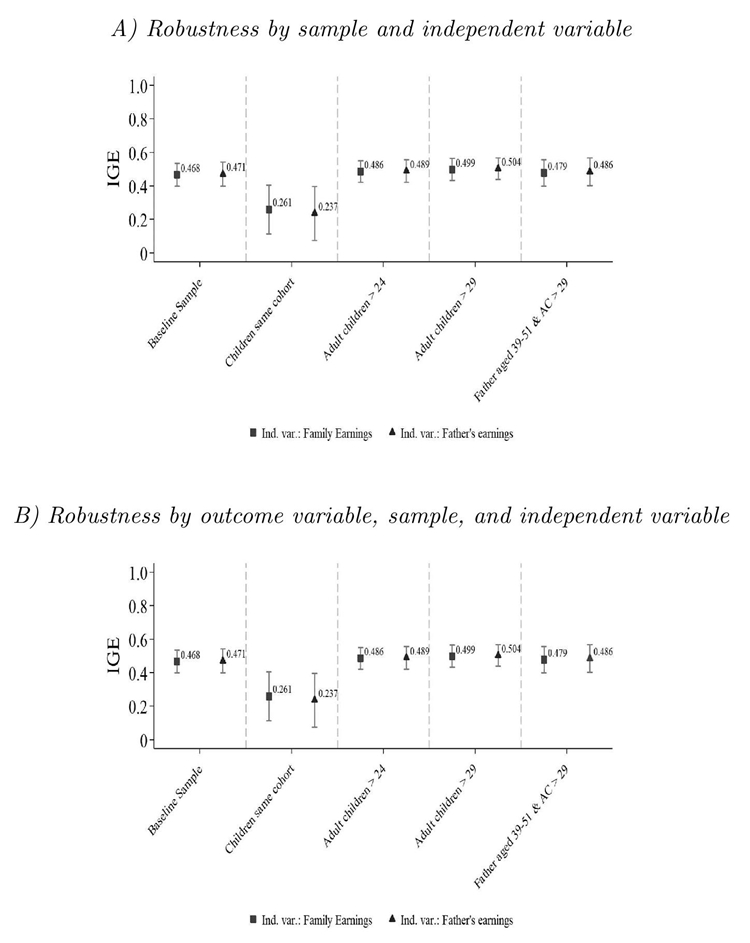
Notes: The figure shows IGE estimates for different samples along with their clustered (within state of birth) confidence intervals at the 95 percent level. The first sample is the baseline, the second focuses on families whose children belong to the same birth cohort to compute family earnings, the third and fourth restrict the age of adult children, while the fifth also restricts the sample to fathers within a specific age range. Panel A employs adult children’s earnings as the outcome variable, while Panel B employs family earnings of adult children as the outcome variable. There are two independent variables: family earnings (squares) and father’s earnings (triangles).

Figure 1 Robustness checks on time-invariant IGE Estimates 

Restricting the sample to families whose children are in the same birth cohort yields an estimate of 0.26, 44 percent lower than the baseline estimate. If the age of adult children is restricted to 25 years or older, the estimate increases to 0.486, and if it is restricted to 29 years or older, it increases to 0.499. Restricting both children’s and fathers’ age leads to an estimate of 0.479, suggesting that considering children between 20 and 24 years old does not substantially decrease the baseline estimate (as suggested by ^{Haider and Solon, 2006}).

A substantial part of the literature has focused on studying fathers’ rather than family earnings (^{Solon, 1999}). We thus test the robustness of our estimates by using synthetic fathers’ instead of family earnings, while also considering different sample characteristics. Figure 1, panel A indicates the corresponding IGE estimates with triangles, along with their 95 percent confidence intervals: considering fathers’ earnings slightly increases the estimates. The IGE estimate with the baseline sample shows that a 1 percent increase in fathers’ earnings is associated with a 0.47 percent increase in adult children’s income. The estimate across samples also remains similar, reaching a maximum value of 0.50 if the sample is restricted to children aged 30 years or older, with a value of 0.49 if fathers’ age is restricted.

A second concern about our IGE estimates is the extent to which economic persistence takes place in family earnings rather than in adult children’s earnings. For this robustness check, we use specification (2), changing the dependent variable to the log of family earnings, that is, adding the earnings of adult children and their spouses. Figure 1, panel B plots these IGE estimates along with their 95 percent confidence intervals across different samples and independent variables. In the baseline sample, the estimates increase substantially, by 22.8 percent with respect to the baseline estimate. The increase is consistent across different samples, with slight differences due to adult children’s age or the use of father’s instead of family earnings as the key independent variable. Although we are not able to formally test the factors driving the IGE upwards, it may be that marital sorting factors lead to a higher level of economic persistence across generations (^{Chadwick and Solon, 2002}; ^{Ermisch et al., 2006}). In this sense, intergenerational mobility in Mexico has an important component derived from marriage decisions.

3.2 Time-variant and cohort-variant IGE estimates

Table 3 reports time-variant (census year) and cohort-variant (birth cohort) IGE trends for the period 1995-2015. As mentioned above, we obtain a census-year trend after setting β=0 and δc , allowing us to estimate the interacting terms between family earnings and census year. Columns (1) and (2) show the census-year trend. Column (1) incorporates only fixed effects for census year, birth cohort, and region of birth, and column (2) also includes life-cycle controls. We also compute a cohort trend, setting β=0 and ρt , which allows us to estimate the interacting terms between family earnings and birth cohorts. The birth cohort trends are shown in columns (3) and (4), where the latter includes life-cycle controls. Column (5) shows the results for our most flexible specification.

In general, table 3 shows a decreasing pattern in the intergenerational elasticity across census years and cohorts. This would suggest that relative intergenerational mobility increased between 1995 and 2015. Most coefficients are positive and statistically significant at the 1 percent level, allowing us to compute IGE estimates for different points in time and specific birth cohorts. With respect to the censusyear trend, column (1) and column (2) show a similar decreasing pattern in the time-variant IGE estimate, where the main difference is that the absence of life-cycle controls yields estimates that are likely to be biased downward. The preferred census-year estimate, shown in column (2), suggests that the IGE decreases from 0.77 in 1995 to 0.67 in 2000, and decreases more in 2010, to 0.47. After that it remains at a similar value for 2015. In fact, by computing confidence intervals at the 95 percent level, it turns out that the decrease in the IGE estimates is particularly significant when comparing estimates for 1995 or 2000 with those for 2010.

For the birth cohort estimates, columns (3) and (4) also show a decreasing pattern, and life-cycle controls play a less important role in their magnitude. The preferred birth cohort estimate, reported in column (4), suggests that the IGE for individuals in the 1971-75 birth cohort is 0.5. The estimate decreases to 0.4 for those in the 1976-80 cohort, and to approximately 0.3 for those in the 1981-85 and 1986-90 birth cohorts. It should be noted that with confidence intervals at the 95 percent level for the point estimates, the IGE differences are statistically significant only when comparing the oldest and youngest cohorts. These results are in line with the census-year trend result, where younger generations have a higher degree of intergenerational mobility.

The last column, which considers our most flexible specification, also supports the argument that intergenerational mobility has increased in recent times, and enables us to determine whether the increase is driven by census-year or birth-cohort effects: the prevailing effect is the one observed across census years. Interpretation of these estimates suggests that people in the 1971-75 birth cohort have an estimated IGE of 0.8 in 1995. This estimate decreases to approximately 0.5 in 2010 and 2015; the estimate for 2000 is not statistically significant. The fact that interactions between cohort and family earnings are not statistically significant indicates that all cohorts follow the same trend.

These results appear to be similar to those from a recent estimate by ^{Torche (2020)}, who builds a socioeconomic index accounting for a family’s durable goods, assets, and services as a proxy for economic persistence across birth cohorts, and finds that intergenerational economic association increases for individuals born between 1950 and 1970, but decreases for younger cohorts.

We also perform robustness checks to test the sensitivity of our preferred IGE estimate, reported in column (2) of table 3. First, we randomly assign a birth state to individuals before computing the IGE estimates; as expected the coefficients are very close to zero. Second, we use the log of fathers’ earnings as the key independent variable, and find similar estimates, with the same pattern in the IGE estimates. Third, we regress the log of family earnings of adult children on the log of synthetic family earnings. These estimates substantially increase with respect to baseline estimates, but the pattern remains similar. Although further research is needed to account for alternative sources of variation, the evidence points to a slight improvement in relative intergenerational economic mobility (that is, lower persistence) in Mexico from 1995 to 2010-2015.

3.3 Regional-variation of the IGE estimate

Table 4 shows the results for IGE by region of birth. As previously explained, we consider four regions: north, center, north-center, and south. Column (1) reports the IGE estimates for the north, column (2) for the center, column (3) for the north-center, and column (4) for the south. All estimates account for census-year fixed effects, birth-cohort fixed effects, and lifecycle factors. In general, the estimates suggest that region of birth plays an important role in intergenerational mobility, and that there is heterogeneous mobility across regions. The highest level of intergenerational mobility is in the north, followed by the center, then the north-center, and finally the south. A 1 percent increase in synthetic family earnings is associated with a 0.43 percent increase in adult children’s earnings in the north, 0.49 percent in the center, 0.52 percent in the north-center, and 0.53 percent in the south. Unfortunately, there is not enough data to identify statistical differences between regions.

These results are in line with recent evidence, coinciding mainly in the fact that the southern region has the lowest level of intergenerational mobility in the country. ^{Delajara and Gran˜a (2018)} and ^{Vélez-Grajales et al. (2018)} used the 2011 ESRU Social Mobility Survey in Mexico to compute relative intergenerational social mobility with a wealth index for the same regions. They find the lowest relative mobility in the south and the highest in the north-central region. More recently, ^{Delajara et al. (2020)} employed the 2017 edition of the same survey to estimate social mobility across the states of Mexico and across wealth ranks. These authors find that southern states have the lowest degree of social mobility (absolute upward mobility), while northern states have the highest (relative and absolute upward mobility).

The robustness checks for these estimates were limited. The first was to consider specification (2). In this case, we examine the interaction between synthetic family earnings and region of birth, with the restrictions β=0 , δc=0 , and ρt=0 The estimates were similar to those in table 4. The second varied both the dependent and independent variables in equation (3) with no major changes. The third considered clustered standard errors, and only the estimate for the southern region turned out not to be statistically significant, which is mainly due to the lack of variation already noted.¹⁶

3.4. Cross-country differences, Mexico, and the Great Gatsby curve

Cross-country differences can shed light on the role of three fundamental factors in determining children’s economic outcomes: family background, labor markets, and the role of the state (^{Solon, 2004}). ^{Corak (2016)} argues that cross-country differences are related to differences in the transmission of inequality due to differences in the investments in children made by different societies, and the return on those investments. These processes include family background (i.e., investment in human capital), labor markets (i.e., returns to education), public policy (i.e., progressive reforms like increasing education and health care for the poor) and their interactions. By understanding how these factors influence intergenerational earnings mobility in Mexico and its differences with other countries, we can understand better what is needed to change the ways in which inequality is transmitted from one generation to the next.¹⁷

To examine the case of Mexico in a cross-country framework, we follow the methodology proposed by ^{Corak (2006)}, which scales the most reasonable IGE estimates for different countries to a representative (anchor) estimate for the U.S., adjusting also for differences in sample characteristics and methods. The anchor is 0.462 for countries other than the U.S., Canada, and the U.K. (Corak, 2006). For Mexico, we consider the IGE estimate based on regressing the log of adult children’s earnings on the log of synthetic fathers’ earnings, controlling for all the factors specified in equation (2) except birth region. This estimate is 0.52. Then, by following a similar specification with PSID data, we estimate an IGE of 0.479, which is similar to the estimate obtained by ^{Grawe (2004)} for the U.S. Finally, by using equation (4) we obtain an IGE of 0.5 for Mexico.

Figure 2 is the Great Gatsby curve that shows how Mexico compares with other countries in terms of intergenerational economic mobility (x-axis) and inequality (y-axis), (^{Corak, 2016}; ^{Krueger, 2012}). In general, the graph suggests a relationship between the transmission of inequality and intergenerational economic mobility (Corak, 2016); it shows that our estimate is similar to those observed for Italy (0.50) and the United Kingdom (0.5), just above Argentina (0.47) and the United States (0.40), and below Chile (0.52) and Brazil (0.58). Mexico shows a low level of economic intergenerational mobility compared with advanced European economies, although it is reasonable for its level of income inequality. However, among similar economies (Argentina, Chile, Brazil, and Peru), Mexico is the least unequal country and has the second highest level of intergenerational mobility.

Figure 2 International comparison: Great Gatsby curve 

This result needs to be interpreted with caution. With the limited available data on earnings, synthetic family earnings are not observed long enough to completely solve the problem of measurement error and attenuation bias (^{Mazumder, 2005}). Better estimates could be computed if data on children and parents were available in the form of surveys or administrative records. However, given the current level of inequality in Mexico, our estimate suggests a reasonable lower bound of intergenerational economic mobility.