Introduction
In Brazil, the Eucalyptus is the genus with the largest area of planted forests, with about 5,56 million hectares. In all this area, 46,1% is destined for the coal industry and industrial wood, 42,1% for pulp and paper and just 4,3% for reconstituted panels sector (Associação Brasileira de Produtores de Florestas Plantadas [Abraf], 2013).
According to Indústria Brasileira de Árvores [IBÁ] (2014), 66,4% of total consumption of wood in natura of Brazilian industries panels are from the Pinus genus and only 31,7% of the Eucalyptus genus.
Most of the Eucalyptus wood volume of short rotation forests is directed to the energy sector, because it is wood from young trees, which are not commonly used in sectors of great economic value as lumber, due to insufficient diameter, or present predominantly juvenile wood, thus resulting in high anisotropy coefficient and growth stresses disturb the drying timber.
On the other hand, these problems arising from juvenile wood that may interfere in any way in certain segments of the forestry industry, are simply eliminated in the particulate panel production process, since the solid wood is reduced to chips and then the particles smaller. Furthermore, authors as Iwakiri, Albuquerque, Prata and Costa (2008a); Mendes, Mendes, Mendonça, Guimarães Júnior and Mori (2014); Gorski, Cunha, Rios, Trianoski and Martarello (2015) concluded that panels produced with species of the genus Eucalyptus showed superior properties to the panels traditionally made of Pinus.
Among the factors that affect the properties of oriented strand board (OSB), the specific gravity panel is one that strongly influence the physical and mechanical properties. The increase in specific gravity results in a higher compression ratio and a consequent increase in the mechanical properties of the panels (Mendes et al., 2008). On the other hand, according to Maloney (1993) and Moslemi (1974), this increase can impair the dimensional stability due to the higher thickness swelling. According to Kelly (1977), the largest amount of particles present on panels with higher densification results in an increased hygroscopic swelling of the wood, due to the release of compressive stress, which acted during the pressing process.
The specific gravity panel produces a large impact on the physical and mechanical properties, and the increased density of the panels results in better mechanical properties; on the other hand, the physical properties are not linearly improved with this increase (Istek and Siradag, 2013).
Studying different densities in particleboard of Toona ciliata, Trianoski, Iwakiri and Matos (2014) noted that the panels produced with lower density adequate the standard minimum requirements, thus reducing the amount of raw material used.
Objectives
This study aimed to determine the influence of specific gravity of OSB produced with five Eucalyptus species on their properties and get linear models between the properties and the densification of the panels.
Materials and methods
Raw material
For this study were used woods of Eucalyptus benthamii, E. dunni, E. grandis, E. saligna and E. urograndis from short rotation plantations with about seven years old, located in Rosario do Sul, Brazil. Were sampled five trees by species, which were cut in logs, after in blocks and then processed to generate Strands.
The particles were produced with nominal dimensions of 80 mm in lenght, 25 mm in width and 0,6 mm in thickness, using a rotating disk chipper with four knives. The particles were dried in a heater at 80°C of temperature to obtain a moisture content of approximately 3%, and then classified manually using a sifter with 9,52 mm of apertures for removal of “fines”.
The resin used was phenol-formaldehyde, with solids content of 51,57% and a viscosity of 503 cP in a proportion of 6% solids based on dry weight of the particles. In order to reduce the hygroscopicity of the panels are also used, 1% wax emulsion.
Panels manufacturing
Three panels for each one of the 14 treatments were manufactured, totaling in 42 OSB panels. The panels were produced in the dimensions of 48 cm × 48 cm × 1,2 cm and two densification, 0,65 g/cm³ and 0,75 g/cm³. The percentage of outer and inner layer was of 20:60:20.
The bonding was done through of a compressor and the air spray gun with a dosing container in a rotary drum. After bonding, the particles were oriented to each layer of the mattress perpendicularly, using a guiding box coupled to the forming box with dimensions of 48 cm × 48 cm × 20 cm. After the formation of the mattress a pre-press was performed to remove air and accommodation of the particles.
The mattress was pressed in a hydraulic press at a temperature of 160 °C, specific pressure of 4 MPa and 10 minutes time pressing.
The produced panels were conditioned in a chamber with temperature of 20 °C ± 3 °C and a relative humidity of 65% ± 5% to reach moisture balance. After stabilization of the panels, the samples were prepared and taken back again to the chamber to get the temperature and constant humidity to perform the physical and mechanical tests.
Physical and mechanical tests
The physical and mechanical tests were performed following the procedures of European standards: Apparent specific gravity (EN 323:2002), water absorption (EN 317:2006), thickness swelling (EN 317:2006), static bending (EN 310:2006) and internal bond (EN 319:2006). The standard EN 300:2006 was used to compare the results.
All statistical analyzes were performed at 95% significance level, using the software Statgraphics Centurion XV, where models were estimated for each property using linear regression.
Results
Physical properties
Table 1 and table 2 presents the linear equations with the determination coefficient and standard error of estimative obtained to water absorption after two and 24 hours of immersion of panels, by species.
Table 1 Estimated equations for water absorption after 2 hours by species.
| Species | Equations | F | R2 | Syx |
|---|---|---|---|---|
| E. benthamii | WA 2h = - 35,6721ASG + 36,6351 | 495,45* | 0,9501 | 0,77 |
| E. dunnii | WA 2h = - 41,9789ASG + 43,6034 | 97,08* | 0,8292 | 1,28 |
| E. grandis | WA 2h = - 35,2343ASG + 35,6076 | 65,98* | 0,7499 | 1,41 |
| E. urograndis | WA 2h = - 38,2368ASG+ 39,1844 | 176,58* | 0,8803 | 1,57 |
| E. saligna | WA 2h = - 44,0301ASG + 42,9089 | 152,31* | 0,8639 | 1,61 |
| Mix | WA 2h = - 38,9708ASG + 39,6259 | 86,97* | 0,7698 | 1,68 |
| P. taeda | WA 2h = - 107,811ASG + 104,017 | 97,08* | 0,7802 | 5,46 |
* Significant at 5% probability of error.
WA 2h = Water Absorption after 2 hours of immersion; ASG = Apparent Specific Gravity.
Table 2 Estimated equations to water absorption after 24 hours by species.
| Species | Equations | F | R2 | Syx |
|---|---|---|---|---|
| E. benthamii | WA 24h = - 90,3628ASG+ 101,351 | 606,39* | 0,9604 | 1,74999 |
| E. dunnii | WA 24h = - 103,901ASG + 117,544 | 123,38* | 0,8205 | 4,61379 |
| E. grandis | WA 24h = - 105,703ASG + 110,95 | 76,75* | 0,7470 | 4,01577 |
| E. urograndis | WA 24h = - 108,903ASG + 116,517 | 243,18* | 0,8967 | 4,22347 |
| E. saligna | WA 24h = - 117,640ASG + 118,594 | 285,76* | 0,9108 | 4,06453 |
| Mix | WA 24h = - 93,6589ASG + 102,314 | 126,25* | 0,8238 | 3,35897 |
| P. taeda | WA 24h = - 123,927ASG + 152,399 | 143,42* | 0,8516 | 5,31435 |
* Significant at 5% probability of error.
WA 24h = Water Absorption after 24 hours of immersion; ASG = Apparent Specific Gravity.
It can be observed that both to WA 2h as to WA 24h were found high determination coefficient values, indicating that the equations obtained explain satisfactorily the linear relationship between the density of panels and water absorption.
To thickness swelling properties after two and 24 hours, not found linear proportionality relationships with the specific gravity of panels to the obtained data in this study.
Mechanical properties of panels
Table 3 and table 4 present the equations with the determination coefficient and the standard error of estimate obtained for the Modulus of Rupture obtained in the direction parallel and perpendicular to plane of panels for each species.
Table 3 Estimated equations to MOR parallel by species.
| Species | Equations | F | R2 | Syx |
|---|---|---|---|---|
| E. benthamii | MOR = 75,5329ASG - 25,7039 | 88,15* | 0,7655 | 3,69 |
| E. dunnii | MOR = 96,1925ASG - 41,9166 | 140,13* | 0,7924 | 4,94 |
| E. grandis | MOR = 94,6051ASG - 32,6963 | 36,04* | 0,6692 | 5,09 |
| E. urograndis | MOR = 104,361ASG - 43,5444 | 104,47* | 0,7844 | 5,89 |
| E. saligna | MOR = 99,3502ASG - 34,5875 | 55,82* | 0,6074 | 5,36 |
| Mix | MOR = 69,2747ASG - 14,9858 | 51,82* | 0,5186 | 5,65 |
| P. taeda | MOR = 97,0801Asg - 32,4374 | 85,84* | 0,7675 | 4,37 |
*Significant at 5% probability of error.
MOR = Modulus of Rupture; ASG = Apparent Specific Gravity.
Table 4 Estimated equations for MOR perpendicular by species.
| Species | Equations | F | R2 | Syx |
|---|---|---|---|---|
| E. benthamii | MOR = 65,6161ASG - 21,2101 | 17,54* | 0,5743 | 5,38 |
| E. dunnii | MOR = 66,2006ASG - 19,7609 | 5,99* | 0,5452 | 4,04 |
| E. grandis | MOR = 54,064ASG - 12,0822 | 17,03* | 0,6301 | 3,46 |
| E. urograndis | MOR = 71,8782ASG - 25,8767 | 27,22* | 0,6447 | 4,41 |
| E. saligna | MOR = 58,9796ASG - 9,22809 | 15,16* | 0,5795 | 4,56 |
| Mix | MOR = 115,408ASG - 59,3886 | 28,39* | 0,6859 | 6,50 |
| P. taeda | MOR = 55,1541ASG - 14,3944 | 22,36* | 0,6507 | 2,88 |
*Significant at 5% probability of error.
MOR = Modulus of Rupture; ASG = Apparent Specific Gravity.
The coefficient of determination values for MOR in parallel and perpendicular direction ranging from 0,5186 to 0,7924 and 0,5452 to 0,6859, respectively. According to the tables, it can be observed that equations obtained from MOR and ASG showed determination coefficient values satisfactory; therefore, equations explain much of the linear interaction between the two properties, showing also the high correlation.
Table 5 and table 6 present the equations together with the determination coefficient and standard error of estimate obtained for the Modulus of Elasticity obtained in the direction parallel and perpendicular to plane of panels to each species.
Table 5 Estimated equations to MOE parallel by species.
| Species | Equations | F | R2 | Syx |
|---|---|---|---|---|
| E. benthamii | MOE = 12502,5ASG - 3444,89 | 311,75* | 0,9203 | 324,58 |
| E. dunnii | MOE = 14686ASG - 4844,47 | 140,13* | 0,8590 | 597,58 |
| E. grandis | MOE = 10684,1ASG - 1780,79 | 36,04* | 0,5297 | 770,97 |
| E. urograndis | MOE = 17568,3ASG - 6431,66 | 104,47* | 0,7946 | 969,51 |
| E. saligna | MOE = 14473,3ASG - 3905,47 | 55,82* | 0,6907 | 650,53 |
| Mix | MOE = 11708,3ASG - 2051,31 | 51,82* | 0,6835 | 674,26 |
| P. taeda | MOE = 8942,08ASG - 1820,85 | 158,48* | 0,8591 | 296,37 |
* Significant at 5% probability of error.
MOE = Modulus of Elasticity; ASG = Apparent Specific Gravity.
Table 6 Estimated equations for MOE perpendicular by species.
| Species | Equations | F | R2 | Syx |
|---|---|---|---|---|
| E. benthamii | MOE = 5947,23ASG - 1603,49 | 23,89* | 0,6476 | 417,76 |
| E. dunnii | MOE = 3785,62ASG + 408,23 | 9,30* | 0,6503 | 185,69 |
| E. grandis | MOE = 3484,69ASG + 286,295 | 10,74* | 0,5179 | 281,05 |
| E. urograndis | MOE = 6184,14ASG -1584,31 | 17,13* | 0,5331 | 477,89 |
| E. saligna | MOE = 3936,57ASG + 622,206 | 7,72* | 0,4124 | 426,12 |
| Mix | MOE = 9868,62ASG - 4432,3 | 16,56* | 0,5602 | 727,34 |
| P. taeda | MOE = 4499,4ASG - 902,16 | 23,19* | 0,6590 | 230,55 |
*Significant at 5% probability of error.
MOE = Modulus of Elasticity; ASG = Apparent Specific Gravity.
It can be observed that the coefficient of determination values for MOE in parallel and perpendicular direction ranging from 0,5297 to 0,9203 and 0,4124 to 0,6590, respectively. As found in the MOR values; probably because they are deeply correlated, the values obtained to MOE showed directly proportional to specific gravity of panels.
Table 7 presents the equations with the coefficient of determination and the standard error of estimate obtained for Internal Bond for each species.
Table 7 Estimated equations for Internal Bond by species.
| Species | Equations | F | R2 | Syx |
|---|---|---|---|---|
| E. benthamii | IB = 1,78893ASG - 0,791231 | 56,52* | 0,7108 | 0,11 |
| E. dunnii | IB = 1,17014ASG - 0,485519 | 33,51* | 0,5827 | 0,09 |
| E. grandis | IB = 1,34317ASG - 0,424055 | 36,61* | 0,5847 | 0,09 |
| E. urograndis | IB = 1,24017ASG - 0,494409 | 82,95* | 0,7904 | 0,06 |
| E. saligna | IB = 1,11112ASG - 0,322361 | 61,04* | 0,7532 | 0,07 |
| Mix | IB = 1,41473ASG - 0,454031 | 38,11* | 0,6558 | 0,08 |
| P. taeda | IB = 0,919355ASG + 0,0140927 | 19,26* | 0,4075 | 0,16 |
*Significant at 5% probability of error.
IB = Internal Bond; ASG = Apparent Specific Gravity.
For Internal Bond, the determination coefficient values ranged from 0,4075 to 0,7904, to P. taeda and E. urograndis, respectively. With exception to P. taeda, the models explain more than 50% of results; thus, the trend of internal bond behavior to the Eucalyptus species was better represented with the equations. The low correlation found between specific gravity and internal bonding was also observed by Iwakiri et al. (2008b), indicating the impossibility of predicting the bond strength based on the specific gravity of the panels at 5% probability of error.
Through of graphs, it was found clearly that WA 2h and WA 24h to the studied species, showed an inversely proportional relationship the ASG of panels. Furthermore, observed that the panels composed of Eucalyptus species showed less propensity to absorption which the panels produced with control species (Pinus taeda).
According to figure 1, among the species the E. saligna was the that suffered the greatest influence of specific gravity in absorption, showing the highest absorption values in panels with lower density, however, the smaller values in panels with higher densification.
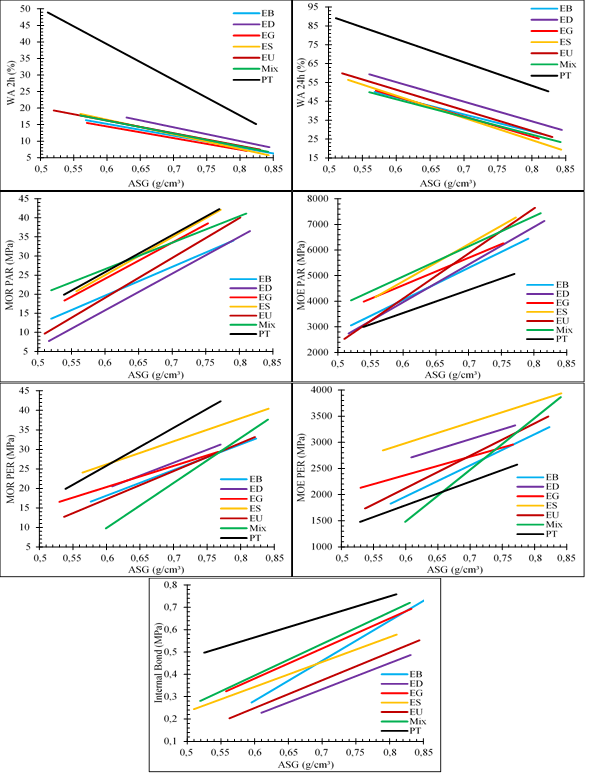
Note: WA = Water Absorption; MOR = Modulus of Rupture; MOE = Modulus of Elasticity; PAR = Paralel; PER = Perpendicular; EB = Eucalyptus benthamii; ED = Eucalyptus dunnii; EG = Eucalyptus grandis; ES = Eucalyptus saligna; EU = Eucalyptus urograndis; PT = Pinus taeda
Figure 1 Graphs with estimated trend lines for physical and mechanical properties of panels as a function of ASG by species
It can be observed in the graphics that the variables MOR and ASG are directly proportional between them, in other words, as higher the specific gravity of panels, a greater Modulus of Rupture tends to be obtained.
To MOE in parallel direction the species showed near, however, a higher data scattering was found to MOE in perpendicular direction; the species E. saligna highlighted with the highest values.
The association between the internal bond and specific gravity of panels according to the graph is of proportionality, thus the resistance accompanied the increase in densification of panels.
Physical properties
According to the results it can be affirmed that the specific gravity of panel exerts a significant influence on absorption properties; therefore, the higher the specific gravity of panels is, the smaller will be the water absorption. Some authors such, as Melo and Dell Menezzi (2010), believe that the higher water absorption in panels of lower density has occurred because there is a greater volume of voids that can be occupied by water.
Under the conditions of this study, and through of shown equations, it can obtain panels with water absorption values preestablished working with the variation of the nominal specific gravity according to the species used, but, generally, for obtaining panels with lower indexes of water absorption, the increasing of density of panels is necessary, however, according to Chen, Du and Wellwood (2010), although, this propertie benefitted from higher panel density, and increasing density means increased manufacturing cost.
The European standard EN 300:2006 does not stipulate maximum values of water absorption to OSB, therefore, it can work with the specific gravity as function of other variables of greatest impact.
Mechanical properties
According with results, the MOR and ASG have a relationship directly proportional, in other words, as higher the specific gravity of panels, a greater Modulus of Rupture tends to be obtained.
The standard EN 300:2006 recommends minimum values of MOR parallel and perpendicular to OSB Class 1 and 2 of 20 MPa and 10 MPa, respectively. Thus, through the equations obtained and in conditions of this study, it can be worked with panels with specific gravity of 0,50 g/cm³ to 0,65 g/cm³ to adequate the parallel MOR requirement and from 0,53 g/cm³ to 0,60 g/cm³ to adequate the perpendicular MOR requirement, according to the species to be used. Therefore, good quality panels can be manufactured having a better utilization of raw materials available, and consequently reducing the amount of components used as the resin, because it is the element of greatest cost in panels production, as well as reducing the weight of the product which implies directly on transportation cost.
For MOE the Mix of species obtained a greater influence of specific gravity, with a significant increase in MOE values according with specific gravity of panels.
According to EN 300:2006, the minimum acceptable values for MOE are 3500 MPa for parallel and 1400 MPa for perpendicular. Based in obtained equations, it can be estimate a specific gravity range of 0,48 g/cm³to 0,60 g/cm³, according to species to obtain MOE values that adequate the minimum standard requirements in parallel direction. For MOE in perpendicular direction, the estimated range of specific gravity to work is 0,27 g/cm³ to 0,60 g/cm³; however, the parallel MOE can be damaged if it is considered a specific gravity value only to adequate MOE values in perpendicular direction.
For internal bond, it is noted that the control species (P. taeda) was highlighted when compared with the other species, it may be linked to fact that P. taeda has a lower wood specific gravity, the main factor contributing to obtaining panels with high compression ratio, high compression ratio value ensures good contact between particles and good densification of panel. Maloney (1993) affirms that a higher compression between particles, the larger amount of resin used effectively between, resulting in good adhesion.
On the other hand, among the species of Eucalyptus, it was observed that the Mix resulted in good internal bond, exceeding the values obtained for each species separately. Thus, it can be affirmed that there was a positive interaction between species, obtaining good results for the property in question.
According to standard EN 300:2006, the minimum acceptable value for internal bond is 0,32 MPa. Through of equations obtained for each species, it is estimated that it can achieve the standard requirement, working under the conditions of this study with specific gravity of panels in the gap of 0,34 g/cm³ to 0,69 g/cm³.
Therefore, through of equations obtained for each species, it is possible to optimize the properties of OSB panels to be produced, making it to achieve pre-determined values by variation of specific gravity of panels.
Conclusions
Based on the results obtained in this study it can be concluded that:
The water absorption has an inverse proportional relationship with the specific gravity of panel.
The relationship between mechanical properties and specific gravity of panel is directly proportional.
Except internal bond, panels produced with the Eucalyptus species showed better properties than those produced with the control species (Pinus taeda).
For internal bond, the Mix balanced the values emphasizing among Eucalyptus species.
The equations obtained for each species showed a good representation of data with satisfactory determination coefficients.
Through of linear models obtained in conditions of this study for each species, it can be estimated the specific gravity to produce OSB panels that will adequate the European standard requirements











 nueva página del texto (beta)
nueva página del texto (beta)


