Introducción
El motor de CD es uno de los actuadores eléctricos de más amplio uso. Su versatilidad, variedad de tamaño y facilidad de control lo hacen preferible sobre los motores de corriente alterna, principalmente en aplicaciones tales como: automatismos, robótica y sistemas mecatrónicos de control de procesos. En la actualidad, el control de velocidad de motores eléctricos en sistemas realimentados, usualmente requiere la incorporación de sensores mecánicos a fin de conocer la posición del rotor y calcular su velocidad para determinar las acciones necesarias de control. Sin embargo, la presencia de estos sensores requiere un espacio adicional en el motor para su montaje y mantenimiento, lo cual eleva el costo del controlador. Por otra parte, los sensores de posición son dispositivos relativamente frágiles y su uso en aplicaciones industriales presenta ciertas desventajas (Montanari et al., 2007; Ilas et al., 1994; De Angelo, 2004). Algunas de estas desventajas son: incremento en el costo, pérdidas por calentamiento, disminución de la confiabilidad debido al incremento en el número de componentes (un mayor número de componentes aumenta la probabilidad de falla originada en alguno de ellos). Una menor inmunidad al ruido es también una desventaja, debido a la conexión física entre el sensor (cables que salen del motor) y la tarjeta de adquisición de datos. Por otro lado, en la operación de motores en ambientes hostiles y de poco espacio no es recomendable el uso de sensores mecánicos. Todo esto indica que eliminar los sensores mecánicos reduce los costos de implementación, reduce los requerimientos de mantenimiento, aumenta la confiabilidad y mejora la inmunidad al ruido del controlador. La tendencia moderna en controladores de velocidad es por tanto, eliminar los sensores de posición y desarrollar métodos de control alternativos (Merabet et al., 2017; Masood et al., 2017; Salas y León, 2006). En Yachiangkam et al. (2004) se presenta un observador adaptivo aplicado en el control de la velocidad de un motor de CD sin sensores mecánicos, la estabilidad del observador se analiza mediante el criterio de Routh-Hurwitz (Ogata, 2010).
En este trabajo se presenta el diseño e implementación de un control de velocidad para un motor de CD de excitación separada, basado en mediciones de la corriente de armadura. La velocidad del motor se estima a través de la técnica de ubicación de polos y el par mecánico se obtiene por medio de un observador de modos deslizantes. Así, el sistema de control se basa en la combinación del algoritmo PI clásico y de la retroalimentación de los estados. El correcto funcionamiento del control propuesto se valida por medio de simulaciones digitales y con pruebas experimentales en tiempo real utilizando un conjunto convertidor CD-CD, motor de CD, sensor de corriente, una tarjeta de adquisición y tarjeta de control.
Modelo del motor de corriente directa
El motor de CD es un actuador electromecánico formado básicamente por un estator o devanado de campo, y un rotor o armadura. El comportamiento dinámico del motor eléctrico se describe generalmente por un sistema de ecuaciones diferenciales, el cual debe reproducir lo más cercano posible los fenómenos eléctricos y mecánicos que están presentes en el motor. La precisión de los resultados del modelo depende del detalle con que se represente la dinámica de estos fenómenos. Tradicionalmente el modelo del motor de CD se desarrolla considerando un sistema magnético lineal con parámetros constantes, donde la corriente de campo de excitación y su flujo magnetizante producido poseen una característica de variación lineal.
El sistema de ecuaciones del modelo general del motor de CD incluye la ecuación de equilibrio de voltaje de ambos circuitos de los devanados (campo y armadura) y las ecuaciones de movimiento rotatorio que involucran las masas del eje. En este trabajo se utiliza un motor en derivación de excitación separada debido a la gran capacidad de regulación de velocidad, facilidad de control y su amplia característica lineal par-velocidad. Estas ventajas del motor de CD de excitación separada lo hacen preferible en máquinas de velocidad variable en las que se necesita amplio margen de velocidad y control fino de la misma. Existen diversos procesos industriales que requieren una exactitud en su control o una gama de velocidades tales como: manipuladores robóticos, vehículos eléctricos, máquinas para rolado de acero, guras eléctricas, máquinas-herramientas, entre otros (Rahman & Mohamed, 2016).
Los motores de excitación separada tienen como característica principal un campo magnético constante en el estator. Esto se logra alimentando el circuito de campo mediante una fuente de voltaje constante, mientras que el circuito del inducido se alimenta de una fuente de voltaje variable (Krause et al., 2002; Chapman, 2012) tal como se muestra en la Figura 1.
Aplicando la ley de voltaje de Kirchhoff al circuito de la Figura 1 y considerar una corriente de campo constante, el modelo matemático que describe el comportamiento de este motor queda representado en espacio de estado de la siguiente manera:
donde ua representa el voltaje de alimentación e ia es la corriente de armadura que circula por la resistencia Ra y a través de la inductancia La de los devanados del rotor. ω es la velocidad del rotor y la salida y del sistema, TL simboliza el par de carga. Mientras que Je y ke son constantes que representan la inercia del rotor de la máquina y fuerza electromotriz, respectivamente. Los valores de las constantes del motor se muestran en la Tabla 1, los cuales se determinaron mediante pruebas experimentales de laboratorio.
Diseño del control
El control de la velocidad del motor de CD se realiza por medio del voltaje de alimentación de la armadura. La Figura 2 muestra el esquema del sistema de control de velocidad propuesto, donde la velocidad del motor se determina a partir de la medición continua de la corriente de armadura ia.
El diseño de control se basa en la técnica de linealización por retroalimentación de estado, en esta técnica el sistema original se transforma en un sistema equivalente de nuevas variables llamado forma canónica controlable, donde el sistema de nuevas variables se expresa en función de las variables de seguimiento de error (Ogata, 2010; Chen, 1999). Una característica fundamental de esta representación es que los estados del sistema son conectados por medio de la rama de realimentación a la entrada de control, donde los polos del sistema son reubicados para lograr una dinámica rápida y estable. En el diseño de control se define una función matemática llamada error de seguimiento y una ley de control, las cuales actúa para hacer que la función de error tienda a cero. La función de seguimiento de error se construye con la diferencia entre la señal de referencia y la señal controlada. Mientras que la ley de control se basa en un algoritmo de control Proporcional e Integral (PI).
La implementación de este algoritmo requiere que el modelo de espacio de estados se pueda expresar en la forma canónica controlable (Ogata, 2010). Aplicando la metodología de transformación, el sistema (1) queda expresado de la siguiente manera:
donde ωref es la señal de referencia de velocidad (valor deseado), el par mecánico TL se asume constante, h representa a y transformada y los estados se definen como:
Así, el algoritmo de controlador PI se puede aplicar directamente al sistema lineal, ya que este se encuentra transformado en la forma canónica controlable. Este control consta de un término de acción proporcional y un término de acción integral, y se representa de la siguiente manera:
donde las Kp y Ki son los parámetros del controlador, cuyos valores se obtienen mediante el método de sintonización de Ziegler-Nichols y se presentan en la Tabla 2.
Observador de la velocidad
La implementación física de la estrategia de control propuesta requiere la realimentación de los estados del sistema, este proceso generalmente se realiza a través de la medición de las variables de estado o por medio de cálculos de las variables físicas utilizando algún método de estimación. En este trabajo se propone estimar la velocidad del rotor a partir de las mediciones de la corriente de armadura, mediante un observador de estados de orden completo. Para aplicar esta técnica, puesto que la corriente de armadura no es la variable controlada, se requiere reordenar la matriz de salida del modelo de espacio de estado del motor,
donde el rango de O es 2. Con esto la condición de observabilidad del sistema se satisface y se dice que el sistema es completamente observable porque todas las transiciones de los estados (ω e ia) afectan continuamente a la salida (ia). El diseño del observador se basa en el enfoque de ubicación de polos, cuyo modelo dinámico queda representado por (5); tal que, los estados
donde
A partir del polinomio característico de A, p = s2 + 102.27s + 375.11, se obtiene la siguiente matriz de transformación (Ogata, 2010),
Para garantizar la precisión y rapidez de convergencia de (5), se seleccionan los valores de -125 + 355.824i y -125 - 355.824i como los polos deseados. Con estos valores se obtiene el polinomio característico deseado pd = s2 + 250s + 142235.71. Así, la matriz de ponderación Ke se calcula multiplicando la matriz Q por un vector de la diferencia entre los coeficientes de los polinomios característicos [pd - p]
La Figura 3 muestra el diagrama a bloques del observador de velocidad de orden completo empleado en este trabajo. Usando el valor obtenido de Ke y conociendo los valores del par mecánico del voltaje y de la corriente de armadura se estima el valor de la velocidad del motor en cada instante de muestreo.
Observador de par mecánico
El par mecánico del motor se estima por medio de un observador de estados con entradas de control discontinuas, el cual se basa en la técnica de modos deslizantes. Las ventajas más importantes de esta técnica son: alta robustez, precisión y rapidez de convergencia en tiempo finito. Para el diseño de este observador se considera lo siguiente: la velocidad del rotor (𝜔) es una variable conocida, ya que se estima por medio del observador de velocidad, la corriente de armadura (ia) se encuentra disponible por medición y el par mecánico (TL) se incorpora como una nueva variable de estado en el sistema original (1). Finalmente, aplicando la formulación de observadores para sistemas lineales e invariantes con el tiempo (Utkin et al., 2009), el sistema queda descrito por las siguientes ecuaciones:
donde
Mientras que v representa la función de entrada discontinua
donde y es la corriente de armadura, que está disponible por medición. El vector de función discontinua obliga a que la diferencia entre las salida del observador de par
Resultados de simulación
En esta sección se muestra la respuesta del controlador propuesto mediante simulación digital. Las simulaciones se realizan en un software especializado en diagrama de bloques utilizando el método de integración de Euler con un paso de integración de h = 10-5 s. El esquema de control implementado, incluyendo los observadores de estado se muestra en la Figura 4.
Para evaluar el desempeño del controlador se analizan diversas simulaciones. A continuación se presenta un caso de estudio representativo, en el cual se programan dos eventos en el par de carga y dos valores de seguimiento de referencia de velocidad. Estos eventos actúan de acuerdo con la siguiente secuencia: el arranque del motor, en t=0, se realiza sin carga (TL = 0) y la velocidad de referencia tiene un valor de 100 rad/s; en el tiempo t=2 s la referencia de velocidad cambia a 120 rad/s; el par de carga se incrementa a 50% de su valor nominal en un tiempo t=3 s; mientras que en t=5 s se aplica el par nominal (TL = 0.9 N.m) de la máquina; como evento final, la velocidad de referencia se incrementa hasta 150 rad/s. El comportamiento de la variable de velocidad y de la corriente de armadura ante los diferentes eventos, se muestra en la Figura 5.
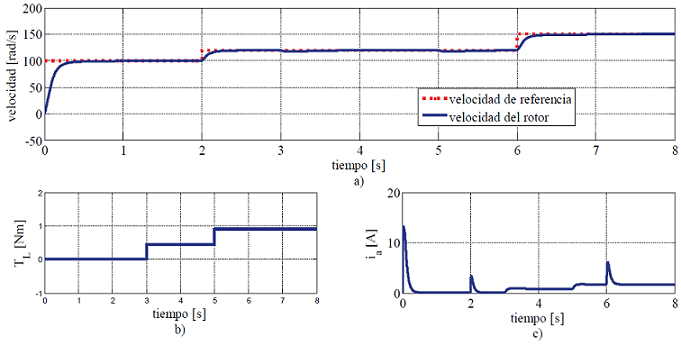
Figura 5 a) Seguimiento de referencia de velocidad, b) par de carga aplicado al motor, c) corriente de armadura o inducido
El controlador propuesto se evalúa de acuerdo con los parámetros de precisión, sobrepaso y rapidez de respuesta. La velocidad del motor presenta gran rapidez de convergencia, tal como se observa en la Figura 5a. Después de un transitorio rápido en el arranque, la velocidad del motor se estabiliza en un tiempo no mayor de 1 s con un error de precisión de velocidad de 0.04%, y no presenta sobrepaso. El error de precisión de seguimiento de velocidad para ωref = 120 rad/s y para ωref = 150 rad/s son 0.025% y 0.086%, respectivamente; en ambos eventos se obtiene un tiempo de convergencia de 0.8 s.
La corriente de armadura en el arranque manifiesta un valor instantáneo máximo de 460% respecto de su valor nominal (ia = 2.8 A) y se estabiliza rápidamente en un tiempo no mayor de 0.8 s, tal como se muestra en la Figura 5c. Durante los cambios en la señal de referencia de velocidad ωref = 120 rad/s y para ωref = 150 rad/s, la corriente alcanza un valor máximo de 3.41 A y 6.1 A, respectivamente. Estos valores de corriente se estabilizan en un intervalo de 0.5 s y 0.8 s, respectivamente. Un resumen de los resultados obtenidos de las pruebas de simulación se muestra en las Tablas 3 y 4.
Tabla 3 Comportamiento de la variable controlada ante los cambios en el par de carga
| Disturbios en el par de carga [N.m] |
Precisión [%] |
Sobrepaso [%] |
Rapidez de convergencia [s] |
|---|---|---|---|
| 0.45 | 0.025 | 0 | 0.95 |
| 0.9 | 0.25 | 0 | 0.85 |
Tabla 4 Comportamiento de la variable controlada ante los cambios en la señal de referencia
| Señal de referencia de velocidad [rad/s] |
Precisión [%] |
Sobrepaso [%] |
Rapidez de convergencia [s] |
|---|---|---|---|
| 100 | 0.04 | 0 | 1.0 |
| 120 | 0.025 | 0 | 0.8 |
| 150 | 0.086 | 0 | 0.8 |
El error de precisión con mayor valor de la variable controlada se presenta durante el seguimiento de referencia ωref = 150 rad/s con una magnitud de 0.25%. El tiempo de respuesta de mayor valor en que la variable controlada alcanza la señal de referencia se presenta en el arranque con un valor de 1.0 s. En ningunos de los eventos se presenta sobrepaso.
Resultados experimentales
En esta sección se muestran los resultados experimentales implementados sobre un prototipo de laboratorio, el cual se forma de los siguientes componentes: una tarjeta DSP1104 para adquisición y procesamiento de datos en tiempo real, una PC para programación y monitoreo, un convertidor CD-CD para alimentar el motor, tarjeta de circuito impreso para acondicionamiento de señales de control, sensor de corriente basado en efecto hall, generador de CD con carga pasiva para aplicar el par mecánico y un motor de CD como planta de control. La representación esquemática del sistema utilizado para la realización de las pruebas se muestra en la Figura 6.
Un convertidor de CD-CD permite convertir un voltaje de CD fijo en un voltaje CD variable. Así, el convertidor representado en la Figura 6 alimenta la armadura del motor de CD con un voltaje entre 0 y 120 V. Esto se logra por medio de la conmutación (encendido y apagado) de un transistor IGBT con base en la técnica de modulación de ancho de pulso (PWM). Con esta técnica se regula el tiempo de encendido y apagado con una frecuencia de conmutación fija de 10kHz. El tiempo de conmutación, en cada periodo, se calcula a través de la tarjeta DSP al comparar una señal portadora (diente de sierra) con la señal proporcionada por la ley de control PID (ua). El resultado de esta comparación (Scontrol) es una señal digital con valores de 0 y 5 V, por lo que se utiliza una tarjeta de acondicionamiento de señal para amplificar el nivel de voltaje a 15 V (Sdisparo), necesario para la activación de la compuerta del disparo del IGBT. Adicionalmente, la tarjeta de acondicionamiento permite aislar eléctricamente el DSP del convertidor de CD-CD.
La tarjeta DSP se programa mediante diagramas de bloques a través del software especializado. Mientras que la supervisión y monitoreo de los datos en tiempo real, se realiza a través de un software de adquisición por medio de la tarjeta DSP1104. La solución del sistema de ecuaciones se realiza por la técnica de integración de Euler con un paso de muestreo τ = 10-4 s. El par mecánico se aplica por medio de un generador de CD acoplado al eje del motor, el cual alimenta una carga pasiva de valor constante. Una vista fotográfica de los componentes del sistema de control se muestra en la Figura 7.
Para comprobar el correcto funcionamiento del control propuesto y el prototipo desarrollado, se realiza una prueba de 22 segundos. Durante este periodo, la velocidad referencia y el par de carga toman diferentes valores en una secuencia de tiempo especificada, tal como se muestra en las Figuras 8 y 9.
La dinámica de la salida de velocidad se muestra en la Figura 10. En el arranque, la velocidad del motor presenta un sobrepaso de 10.5%, después del transitorio se estabiliza en un intervalo de 1.54 s y alcanza su valor de estado estable con un error de precisión de 0.4%. Mientras que el error de precisión de seguimiento de velocidad para ωref = 120 rad/s y para ωref = 150 rad/s son 0.025% y 0.6%, respectivamente; para estos eventos se alcanza el estado estable en 1.68 s y 1.56 s, respectivamente.
La corriente de armadura en el arranque manifiesta un valor instantáneo máximo de 128.8% respecto de su valor nominal (ia = 2.8 A) y se estabiliza en un tiempo no mayor de 1.18 s (Figura 11). Durante los cambios en la señal de referencia de velocidad ωref = 120 rad/s y para ωref = 150 rad/s, la corriente alcanza un valor máximo de 1.015 A y 2.656 A, y se estabilizan en un intervalo de 1.22 s y 1.83 s, respectivamente. Un resumen de los resultados obtenidos de las pruebas experimentales se muestra en las Tablas 5 y 6.
Tabla 5 Comportamiento de la variable controlada ante los cambios en el par de carga
| Disturbios en el par de carga [N.m] |
Precisión [%] |
Sobrepaso [%] |
Rapidez de convergencia [s] |
|---|---|---|---|
| 0.0 | 0.4 | 10.5 | 1.54 |
| 0.9 | 1.0 | 0 | 1.5 |
Tabla 6 Comportamiento de la variable controlada ante los cambios en la señal de referencia
| Señal de referencia de velocidad [rad/s] |
Precisión [%] |
Sobrepaso [%] |
Rapidez de convergencia [s] |
|---|---|---|---|
| 100 | 0.4 | 10.5 | 1.54 |
| 120 | 0.025 | 1.66 | 1.68 |
| 150 | 0.60 | 2.13 | 1.56 |
El error de precisión de mayor valor de la variable controlada se presenta durante el seguimiento de referencia ωref = 100 rad/s con una magnitud de 0.4%. El tiempo de respuesta de mayor valor en que la variable controlada alcanza la señal de referencia, se presenta durante el seguimiento de velocidad de referencia de ωref = 150 rad/s con un valor de 1.83 s. Este tiempo se debe a que el motor opera con su par de carga nominal y una velocidad cercana a su valor nominal. Mientras que el sobrepaso de mayor valor se presenta durante el arranque de 10.5%. Esto es resultado de que el motor arranca desde una velocidad de 0 rad/s y en condiciones de vacío.
Conclusiones
En este trabajo se ha presentado un control de velocidad para un motor de CD sin sensores mecánicos (encoders), el lazo de retroalimentación solo requiere la medición continua de la corriente de armadura. La velocidad de motor se estima en tiempo real a través de un observador de estados y un observador de par.
Los resultados de las pruebas experimentales y de simulación demuestran que el controlador propuesto es capaz de mantener la velocidad en el valor deseado con una precisión menor a 1%, una velocidad de convergencia menor a 1.7 s y un sobrepaso menor a 11%.
El control propuesto es una alternativa de menor costo en comparación con los controladores de velocidad que utilizan encoders, ya que estos dispositivos son mucho más costosos en comparación con los sensores de corriente.











 nueva página del texto (beta)
nueva página del texto (beta)













