Introducción
La extrusión de perfiles de aluminio es uno de los métodos más empleados en el proceso de conformado (Borowski & Wendland, 2016). En este proceso, el componente más importante es la matriz de extrusión debido a las condiciones de trabajo a las que está expuesta (altas presiones y temperaturas) y a la responsabilidad funcional dentro del proceso, pues determina la configuración geométrica de la pieza (Tingting et al., 2013).
El fenómeno del desgaste se inicia producto a la unión por interferencia que se produce en la zona de contacto de la herramienta y la pieza en bruto. La carga compresiva provoca que las presiones locales sean extremadamente altas (Lepadatu et al., 2006).
La simulación por el Método de Elementos Finitos (MEF) no puede proporcionar soluciones absolutas, puesto que los modelos físicos abstraen e idealizan los sistemas reales de interés para cumplir con las suposiciones de las teorías físicas (Wang, 2017).
No obstante, la simulación por el MEF del desgaste es una técnica que presenta grandes ventajas para la mejora del diseño de componentes del proceso de conformado (Cruzado et al., 2010). Existen autores que han empleado el MEF como una técnica efectiva en el estudio del comportamiento del proceso de extrusión, entre ellos cabe destacar a Lepadatu et al. (2006), quienes en su investigación predicen el fenómeno del desgaste en matrices de extrusión, al realizar una simulación por el MEF que incluye el modelo de desgaste de Archard.
Nowotynska & Kut (2014) realizan análisis experimentales de los esfuerzos y del fenómeno del desgaste en matrices de extrusión, al variar el ángulo de la herramienta; y emplean como técnica de validación el MEF.
Asimismo, Tingting et al. (2013) estudian, utilizando el MEF, la intensidad del desgaste basados en la modificación del modelo de desgaste de Archard, pues tienen en cuenta la termo-dependencia de las propiedades mecánicas de los materiales, en especial el coeficiente de Archard.
De igual manera, Lee & Im (1999) estudian el comportamiento del desgaste en matrices de extrusión directa, implementando el modelo de desgaste de Archard, a partir de un análisis por el MEF. Los autores refieren que los resultados obtenidos a través de las simulaciones numéricas coinciden con lo planteado en la literatura especializada en cuanto al área e intensidad del desgaste en la matriz.
El diseño de experimentos es un conjunto de técnicas activas que consisten en planear y realizar un conjunto de pruebas con el objetivo de generar datos que, al ser analizados estadísticamente, proporcionen evidencias objetivas que permitan responder las interrogantes planteadas por el experimentador sobre determinada situación (Gutiérrez & de la Vara, 2008). Entre los diseños experimentales se encuentra el diseño factorial fraccionado Plackett-Burman (DPB), que tiene como ventajas, al ser comparado con el diseño factorial completo convencional, la reducción significativa del número de experimentos necesarios para alcanzar con efectividad el objetivo de la experimentación (Vanaja & Shobha, 2007).
El fenómeno de desgaste que ocurre durante el proceso de extrusión en la matriz es complejo y poco controlable, depende de varios parámetros de funcionamiento y geométricos (Lepadatu et al., 2006), por tanto, es importante determinar la real influencia que dichos parámetros tienen sobre el desgaste.
El objetivo de esta investigación es presentar el análisis del comportamiento de la intensidad del desgaste en una matriz de extrusión directa en frío de barras cilíndricas de aleaciones de aluminio, durante el proceso completo, a partir del MEF, utilizando el ampliamente aceptado modelo de desgaste de Archard.
Materiales y métodos
Modelo de desgaste de Archard
Dos tercios de todos los tipos de desgaste que se encuentran en la industria ocurren debido a los mecanismos de desgaste adhesivo y abrasivo (Menezes et al., 2013). En el proceso de extrusión el desgaste abrasivo es el mecanismo dominante. Este desgaste ocurre cuando los componentes metálicos se deslizan uno contra otro bajo grandes presiones (Lepadatu et al., 2006). Lo cual se corrobora por Ramesh et al. (2011), quienes en su investigación declaran, de igual manera, al desgaste abrasivo como principal mecanismo de desgaste de la matriz.
El modelo de Archard describe al desgaste, como el colapso de los picos presentes en la superficie rugosa de los objetos que están en contacto unos con otros y experimentan un movimiento relativo entre ellos (Klassen et al., 2014). La ecuación de Archard (1) caracteriza analíticamente la intensidad del desgaste.
Donde:
p = |
presión normal entre la pieza en bruto y la matriz |
v = |
velocidad de deslizamiento |
H = |
dureza del material de la matriz y |
t = |
tiempo |
Se ha modificado el modelo de Archard con la adición de exponentes experimentales: m=1, n=1 y a=2 (Levy & Van, 2015); estos valores son sugeridos por el programa DEFORMTM-2D.
El coeficiente K expresa la probabilidad de la generación de partículas abrasivas (Lepadatu et al., 2006; Põdra & Andersson, 1999). En esta investigación se emplea un valor de 10-4, como valor nominal que caracteriza el contacto entre las superficies; este valor también es utilizado por Nowotynska & Kut (2014) y Lee & Im (1999).
Factores geométricos de la matriz de extrusión directa
El proceso de extrusión directa comprende varios factores tanto geométricos: la razón de extrusión, el ángulo de la matriz y el factor de forma; así como de funcionamiento: lubricación, temperatura del proceso y velocidad de extrusión (Kalpakjian & Schmid, 2002). Existen autores como Mallo (1986) que relacionan otros factores como parte de este proceso como los radios de entrada (R1 y R2) y el apoyo en la zona de extrusión.
El modelo CAD (del inglés Computer Aid Desing) de la matriz, empleado en la investigación, es simétrico por el eje, en el mismo se varían los factores geométricos (Figura 1). Esta configuración geométrica bidimensional (2D) permite disminuir el costo computacional, puesto que se requieren menos elementos de malla y condiciones de contacto más simples en comparación con los modelos tridimensionales (3D).
Diseño estadístico Plackett-Burman
El DPB se emplea para indicar dos niveles en factores (de un proceso), aunque se pueden especificar más niveles. Este diseño estadístico permite una estimación eficiente de los principales efectos analizados (Vanaja et al., 2007). Este es un método que presenta un nivel de resolución III, lo que significa que se puede determinar el efecto principal de cada factor analizado sobre la respuesta medida.
En este trabajo se realiza una selección de los niveles de los factores: coeficiente de fricción entre la matriz y la pieza en bruto (establecido en estudios experimentales del proceso de extrusión de aleaciones de aluminio), ángulo de incidencia de la matriz de extrusión, razón de extrusión, las diversas longitudes del apoyo en la entrada y los radios de entrada de la matriz, los cuales se encuentran enmarcados en los rangos de operatividad mínimos y máximos que han reportado en sus investigaciones autores como: Lepadatu et al. (2006); Chen et al. (2007); Noorani et al. (2005); Bingöl et al. (2015); Mallo (1986), Ridzuan et al. (2014) y Fereshteh et al. (2013). Este análisis de la literatura especializada permite contar con valores coherentes y fiables para definir los parámetros de la simulación numérica del proceso de extrusión que se realiza en esta investigación (Tabla 1).
Tabla 1: Codificación de los niveles y factores del DPB
| Factor | Código | Unidad | Valor máximo (+1) | Valor mínimo (-1) |
| Ángulo de la matriz de extrusión |
A | Grados | 60 | 30 |
| Razón de extrusión | B | % | 75 | 16.667 |
| Coeficiente de fricción |
C | ----- | 0.4 | 0.15 |
| Radio de entrada 1 (R1) |
D | mm | 5 | 0.3 |
| Radio de entrada 2 (R2) |
E | mm | 1 | 0.5 |
| Longitud de apoyo en la entrada |
F | mm | 20 | 5 |
Condiciones de simulación del proceso de extrusión
La simulación numérica del proceso de extrusión directa en frío de aleaciones de aluminio se realiza utilizando el programa DEFORMTM-2D, a partir de las combinaciones mostradas en la Tabla 2. La pieza en bruto es cilíndrica y las principales dimensiones son el diámetro inicial de 100 mm y la longitud de 100 mm.
Tabla 2: Matriz experimental del DPB para el análisis del desgaste en la matriz de extrusión
| Factores | ||||||
| Ensayo | A | B | C | D | E | F |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | -1 | +1 | +1 | -1 | +1 | -1 |
| 3 | -1 | +1 | -1 | -1 | -1 | +1 |
| 4 | +1 | +1 | -1 | +1 | +1 | -1 |
| 5 | -1 | +1 | +1 | +1 | -1 | +1 |
| 6 | -1 | -1 | +1 | +1 | +1 | -1 |
| 7 | +1 | +1 | -1 | +1 | -1 | -1 |
| 8 | -1 | -1 | -1 | +1 | +1 | +1 |
| 9 | -1 | -1 | -1 | -1 | +1 | -1 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | +1 | -1 | +1 | -1 | -1 | -1 |
| 12 | +1 | -1 | -1 | -1 | -1 | +1 |
| 13 | +1 | -1 | +1 | +1 | +1 | +1 |
| 14 | +1 | +1 | +1 | -1 | -1 | +1 |
Dentro de las condiciones de simulación numérica del proceso de extrusión cabe destacar:
La temperatura inicial del proceso es de 20 °C para todos los componentes.
El coeficiente de transferencia de calor entre la matriz y la pieza en bruto se establece en 11 N/sec·mm·°C. En aras de simplificar la simulación se asume que el proceso es adiabático, pues la disipación del calor en un proceso de conformado en frío no se considera un factor importante.
La velocidad de desplazamiento del pistón es de 0.4 mm/min y se mantiene constante a lo largo del proceso. Esta suposición es posible realizarla, pues la variación de la velocidad durante un proceso real de extrusión no es significativa.
Los coeficientes de fricción y de desgaste de Archard (K) inciden en todas las zonas de la interfaz matriz-pieza en bruto y son invariantes durante el transcurso del proceso. Aunque el acabado superficial de las matrices, empleadas en procesos reales de extrusión, no se comporta constante, modelar la rugosidad en la superficie de contacto para luego simular numéricamente el comportamiento de la interfaz matriz-pieza en bruto y la acción del coeficiente de Archard, resulta complejo y costoso en términos de tiempo y de capacidad de cómputo.
La dureza de la matriz es de 62 HRC.
Se considera el material de la pieza en bruto completamente plástico y rígido el material de la matriz, lo cual según Wang (2017) se acepta en simulaciones por el MEF, donde la deformación del material sea grande.
Evidentemente, las simplificaciones en el modelo de análisis por el MEF del proceso de extrusión provocan que existan diferencias respecto al proceso de extrusión real, lo que implica que los resultados no sean totalmente coincidentes. Sin embargo, es importante recordar que el MEF es un método de aproximación de los resultados al comportamiento real de los sistemas analizados; el cual según Wang (2017) es ampliamente utilizado en diferentes escenarios de deformación para el análisis de disímiles fenómenos físicos, permite encausar el diseño y el análisis ingenieril, y eventualmente apoyar las soluciones de diseño y la actividad productiva.
Material de la matriz de extrusión y de la pieza en bruto
El material de la matriz es el acero AISI D2, que es ampliamente utilizado en la fabricación de matrices para el proceso de extrusión en frío; el material de la pieza de trabajo es el aluminio 6061-O. En la Tabla 3 se muestran las principales propiedades de los materiales.
Tabla 3: Propiedades mecánicas del material de la matriz y la pieza en bruto (DEFORMTM-2D, 2009), (Lingaiah, 2004) y (MatWeb, 2016)
| Material | Límite de rotura |
Límite elástico |
Módulo elástico |
Coeficiente de Poisson |
| 6061-O | 125 MPa | 55 MPa | 68.9 GPa | 0.3 |
| AISI D2 | 2200 MPa | --- | 209.9 GPa | 0.3 |
Las ecuaciones (2, 3, 4 y 5) caracterizan la curva de esfuerzo de fluencia-deformación del material de la pieza en bruto, a 20 °C, 100 °C, 200 °C y 300 °C (Figura 2.), las que se obtienen a partir de la base de datos del programa de simulación empleado (DEFORMTM-2D, 2009). El aumento de la temperatura mejora el comportamiento plástico del material que se extruye.
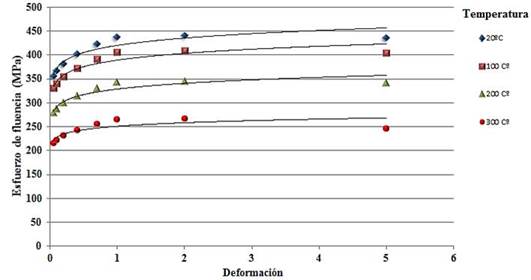
Figura 2: Curva de esfuerzo de fluencia-deformación del aluminio 6061-O atendiendo a la variación de temperatura (DEFORMTM-2D, 2009)
La variación de la temperatura en intervalos por encima de 400 °C provocan cambios significativos en la dureza del material y en el coeficiente de desgaste de Archard (Tingting et al., 2013). En esta investigación la temperatura del proceso de extrusión no alcanza grandes valores, por tanto, su influencia no es considerada significativa toda vez que se establece que el proceso ocurre por debajo de la temperatura de recristalización del material de la pieza en bruto.
Análisis numérico del proceso de extrusión
El modelo desarrollado para la simulación del proceso de extrusión es de dos dimensiones, el pistón y la matriz se consideran rígidos y la pieza en bruto tiene un comportamiento plástico. El modelo de resolución empleado es el Lagrangian Incremental a partir del cual la malla se genera en la pieza en bruto a medida que esta se deforma, lo que permite determinar acertadamente el flujo del material. Las características de la malla empleada en las simulaciones se muestran en la Tabla 4, el tipo de elemento es de superficie cuadrilátero de 4 nodos.
Tabla 4: Características de la malla
| Características | Matriz | Pieza en bruto |
| Cantidad de elementos | 5000 | 2500 |
| Tamaño global de los elementos | 4 mm | 4 mm |
| Razón de tamaño de los elementos | 2 | 2 |
| Tolerancia | 0.01 | 0.01 |
En las zonas que se encuentran en contacto, el tamaño de los elementos de la malla es menor que el valor definido en la Tabla 4, lo que permite garantizar una mejor precisión de los resultados (Figura 3).
Durante el proceso de extrusión la presión normal en la interfaz matriz-pieza en bruto, la temperatura y la velocidad de conformado están constantemente variando a partir de la posición y el tiempo. El desplazamiento y la presión para cada posición pueden obtenerse a partir del programa DEFORMTM-3D (2D), entonces, el incremento de la intensidad del desgaste en la matriz en cada instante de tiempo puede ser calculado por la definición 6, de acuerdo con lo planteado por Tingting et al. (2013).
Discusión y análisis de resultados
Intensidad del desgaste en la zona de incidencia principal de la matriz de extrusión
Con el objetivo de especificar el efecto, a partir de las simulaciones por el MEF, que los factores geométricos tienen sobre la intensidad del desgaste de las matrices de extrusión, se establecieron 20 puntos de medición para calcular el desgaste promedio en la Zona de Incidencia Principal (ZIP) de la herramienta, comprendida desde el R1 hasta el final del apoyo de la entrada (Figura 4).
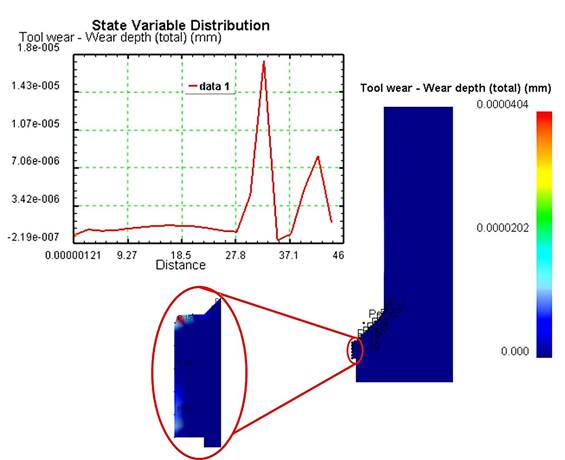
Figura 4: Puntos de medición del valor de la intensidad del desgaste en la ZIP de la matriz de extrusión 1 a 70.8 mm de desplazamiento del pistón
Existe desgaste en toda la ZIP de la matriz, se observa que la máxima intensidad del desgaste, se encuentra en el radio de entrada R2, esta área garantiza la existencia de un adecuado flujo del material extruido y es donde comienza el proceso de extrusión del perfil, por tanto, es una de las zonas más propensas al desgaste. Además, existe otra área crítica, el apoyo de la entrada, en la cual ocurre un prolongado contacto entre la pieza en bruto y la matriz.
La ubicación de las zonas con mayor desgaste determinadas en esta investigación tiene plena correspondencia con los resultados alcanzados por Lee & Im (1999), Lepadatu et al. (2006) y Tingting et al. (2013), quienes a pesar de emplear condiciones y parámetros diferentes en el proceso de extrusión destacan en su totalidad que es la ZIP la que mayor comprometimiento funcional presenta ante el fenómeno del desgaste.
Las mediciones se realizaron atendiendo al desplazamiento del punzón en la matriz para los diferentes ensayos realizados; en la Figura 5 se muestra el ensayo 1.
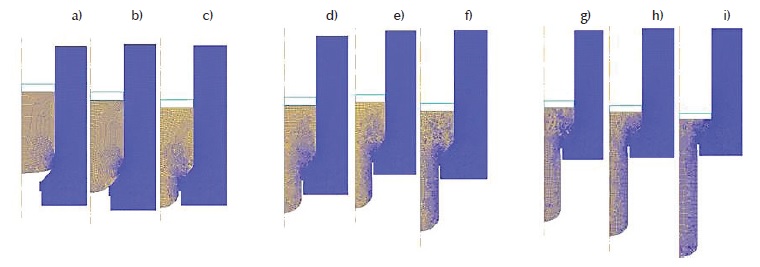
Figura 5: Evolución del proceso de extrusión atendiendo a los desplazamientos del pistón; a) 9.24 mm; b) 19.2 mm; c) 29.5 mm; d) 39.5 mm; e) 50.3 mm; f) 60.6 mm; g) 70.8 mm; h) 80.7 mm y i) 95 mm
Las Tablas 5, 6 y 7 muestran los valores registrados en los 20 puntos del ensayo 1 atendiendo al desplazamiento del pistón. La evolución del desgaste en la ZIP de la matriz, ocurre a medida que avanza la pieza en bruto en el interior de dicha herramienta. Se registra un aumento paulatino de la magnitud de la intensidad del desgaste, lo que evidencia el carácter acumulativo que tiene este fenómeno.
Tabla 5: Puntos de medición del valor de la intensidad del desgaste en la ZIP de la matriz de extrusión del ensayo 1, en la etapa inicial del proceso (Figuras 5a, b y c)
| Puntos/Distancia del pistón |
9.4 mm | 19.2 mm | 29.5 mm |
| 1 | 6.85·10-7 | 2.62·10-8 | 1.03·10-7 |
| 2 | 6.73·10-7 | 9.67·10-7 | 9.98·10-7 |
| 3 | 3.05·10-7 | 5.86·10-7 | 6.46·10-7 |
| 4 | 1.51·10-8 | 4.97·10-7 | 4.95·10-7 |
| 5 | 0 | 3.64·10-7 | 4.95·10-7 |
| 6 | 0 | 3.15·10-7 | 4.74·10-7 |
| 7 | 0 | 3.49·10-7 | 5.21·10-7 |
| 8 | 0 | 3.29·10-7 | 5.13·10-7 |
| 9 | 0 | 3.13·10-7 | 5.04·10-7 |
| 10 | 0 | 3.04·10-7 | 5.08·10-7 |
| 11 | 0 | 1.92·10-7 | 4.27·10-7 |
| 12 | 0 | 6.27·10-8 | 3.86·10-7 |
| 13 | 0 | 7.40·10-9 | 1.86·10-7 |
| 14 | 0 | 5.59·10-8 | 6.24·10-7 |
| 15 | 0 | 3.54·10-23 | 1.77·10-6 |
| 16 | 0 | 0 | 6.79·10-8 |
| 17 | 0 | 0 | 2.52·10-7 |
| 18 | 0 | 0 | 4.78·10-7 |
| 19 | 0 | 0 | 7.07·10-7 |
| 20 | 0 | 0 | 5.97·10-8 |
| Promedio (mm) | 8.39·10-8 | 2.18·10-7 | 5.11·10-7 |
Tabla 6: Puntos de medición del valor de la intensidad del desgaste en la ZIP de la matriz de extrusión del ensayo 1, en la etapa intermedia del proceso (Figuras 5d, e y f)
| Puntos/Distancia del pistón |
39.5 mm | 50.3 mm | 60.6 mm |
| 1 | 1.99·10-7 | 3.14·10-7 | 4.45·10-7 |
| 2 | 1.02·10-6 | 1.05·10-6 | 1.08·10-6 |
| 3 | 7.13·10-7 | 7.92·10-7 | 8.76·10-7 |
| 4 | 5.99·10-7 | 7.24·10-7 | 8.59·10-7 |
| 5 | 6.37·10-7 | 8.06·10-7 | 9.87·10-7 |
| 6 | 6.51·10-7 | 8.54·10-7 | 1.07·10-6 |
| 7 | 7.19·10-7 | 9.45·10-7 | 1.18·10-6 |
| 8 | 7.23·10-7 | 9.55·10-7 | 1.20·10-6 |
| 9 | 7.15·10-7 | 9.46·10-7 | 1.18·10-6 |
| 10 | 7.00·10-7 | 9.18·10-7 | 1.14·10-6 |
| 11 | 5.88·10-7 | 7.83E-07 | 9.82·10-7 |
| 12 | 5.13·10-7 | 6.55·10-7 | 8.20·10-7 |
| 13 | 3.27·10-7 | 5.05·10-7 | 6.85·10-7 |
| 14 | 1.29·10-6 | 2.27·10-6 | 3.36·10-6 |
| 15 | 5.08·10-6 | 8.95·10-6 | 1.26·10-5 |
| 16 | 6.79·10-8 | 6.79·10-8 | 6.79·10-8 |
| 17 | 3.95·10-7 | 4.66·10-7 | 6.25·10-7 |
| 18 | 1.57·10-6 | 2.81·10-6 | 3.90·10-6 |
| 19 | 2.13·10-6 | 3.86·10-6 | 588·10-6 |
| 20 | 3.75·10-7 | 9.24·10-7 | 1.39·10-6 |
| Promedio (mm) | 9.51·10-7 | 1.48·10-6 | 2.02·10-6 |
Tabla 7: Puntos de medición del valor de la intensidad del desgaste en la ZIP de la matriz de extrusión del ensayo 1, en la etapa final del proceso (Figuras 5h, i, j).
| Puntos/Distancia del pistón |
70.8 mm | 80.7 mm | 95 mm |
| 1 | 5.92·10-7 | 7.13·10-7 | 1.14·10-6 |
| 2 | 1.11·10-6 | 1.15·10-6 | 1.27·10-6 |
| 3 | 9.81·10-7 | 1.11·10-6 | 1.57·10-6 |
| 4 | 1.03·10-6 | 1.24·10-6 | 1.86·10-6 |
| 5 | 1.21·10-6 | 1.48·10-6 | 2.18·10-6 |
| 6 | 1.33·10-6 | 1.64·10-6 | 2.36·10-6 |
| 7 | 1.47·10-6 | 1.80·10-6 | 2.51·10-6 |
| 8 | 1.50·10-6 | 1.83·10-6 | 2.51·10-6 |
| 9 | 1.48·10-6 | 1.79·10-6 | 2.44·10-6 |
| 10 | 1.40·10-6 | 1.68·10-6 | 2.31·10-6 |
| 11 | 1.21·10-6 | 1.45·10-6 | 2.06·10-6 |
| 12 | 9.93·10-7 | 1.18·10-6 | 1.67·10-6 |
| 13 | 8.88·10-7 | 1.10·10-6 | 1.53·10-6 |
| 14 | 4.47·10-6 | 5.68·10-6 | 7.94·10-6 |
| 15 | 1.74·10-5 | 2.12·10-5 | 2.84·10-5 |
| 16 | 6.79·10-8 | 6.79·10-8 | 6.97·10-8 |
| 17 | 6.79E-07 | 7.93·10-7 | 8.14·10-7 |
| 18 | 5.09·10-6 | 6.50·10-6 | 7.28·10-6 |
| 19 | 8.21·10-6 | 1.07·10-5 | 1.4·10-5 |
| 20 | 1.08·10-6 | 2.53·10-6 | 3.53·10-6 |
| Promedio (mm) | 2.61·10-6 | 3.28·10-6 | 4.37·10-6 |
En los primeros milímetros de avance del pistón el desgaste en la matriz se encuentra en la zona inicial de contacto, lo que se evidencia claramente en los valores registrados en la Tabla 5, mientras que a medida que avanza la pieza en bruto por el espacio de extrusión ocurre un aumento de la intensidad del desgaste hacia la zona final de contacto de la ZIP (Tablas 6 y 7).
Determinación de la intensidad del desgaste promedio en la ZIP de la matriz de extrusión
Se determina el desgaste en la ZIP en todos los instantes de tiempo establecidos por el desplazamiento del pistón para todos los ensayos, según la ecuación 7.
Donde:
Wp = |
desgaste promedio en cada desplazamiento del pistón (mm) |
Wi = |
desgaste puntual en cada desplazamiento del pistón analizado (mm) |
N = |
cantidad de puntos analizados |
La Tabla 8 muestra los valores del desgaste promedio en la ZIP del conjunto de matrices estudiadas, a lo largo de todos los instantes de tiempo, dichos valores fueron empleados en el análisis de varianza.
Tabla 8: Valores del desgaste promedio de las matrices estudiadas a partir del DPB
| Ensayo | Desgaste promedio (mm) |
| 1 | 1.72·10-6 |
| 2 | 2.58·10-6 |
| 3 | 8.81·10-6 |
| 4 | 3.63·10-5 |
| 5 | 2.68·10-6 |
| 6 | 9.32·10-7 |
| 7 | 2.79·10-5 |
| 8 | 1.61·10-6 |
| 9 | 2.2·10-6 |
| 10 | 1.72·10-6 |
| 11 | 3.89·10-7 |
| 12 | 6.43·10-7 |
| 13 | 7.01·10-7 |
| 14 | 9.51·10-6 |
Se realiza un análisis de convergencia del mallado en todos los ensayos a partir de la matriz de experimentación, propuesta en la Tabla 2, para tal propósito se varía el tamaño global del elemento de malla a la mitad (2 mm). En ningún ensayo se detectaron diferencias significativas en los resultados, el error promedio está cerca de 5 %.
La Figura 6 muestra el comportamiento de la intensidad del desgaste en la ZIP ante la variación del tamaño de los elementos de la malla. Las curvas tienen un comportamiento similar en todos los puntos analizados.
Análisis de la influencia de los parámetros geométricos de la matriz sobre la intensidad del desgaste
El análisis de varianza se muestra en la Tabla 9; los factores A, B, C, D y F son los que tienen una influencia significativa sobre el fenómeno del desgaste en la matriz (P < 0.05; para 95 % de probabilidad de diferencias significativas). El coeficiente R2 indica que el modelo matemático mostrado en la ecuación (4) explica un 92.2563 % de la variabilidad de la respuesta (intensidad del desgaste).
Tabla 9: Análisis de varianza de los factores geométricos de la matriz de extrusión directa en frío
| Factor | Suma de cuadrados | Gl | Cuadrado medio | Razón-F | Valor-P |
| A | 267.2558467 | 1 | 267.2558467 | 14.99 | 0.0061* |
| B | 550.8752521 | 1 | 550.8752521 | 30.90 | 0.0009* |
| C | 306.7475201 | 1 | 306.7475201 | 17.21 | 0.0043* |
| D | 176.2643401 | 1 | 176.2643401 | 9.89 | 0.0163* |
| E | 6.59341875 | 1 | 6.59341875 | 0.37 | 0.5623 |
| F | 179.0037008 | 1 | 179.0037008 | 10.04 | 0.0157* |
| Error total | 124.7919719 | 7 | 17.82742455 | ||
| Total (corr.) | 1611.53205 | 13 | |||
| *Valor de probabilidad significativo (95 %). | |||||
El diagrama de Pareto muestra, de igual manera, los factores significativos y el modo en que estos influyen en la intensidad del desgaste (Figura 7). Asimismo, dicho diagrama permite jerarquizar los factores de acuerdo con su nivel de influencia, lo cual garantiza el análisis individual de los mismos en función del desgaste de la herramienta.
El aumento de la razón de extrusión influye positivamente en el valor de la intensidad del desgaste, debido a que en medida que se reduce la sección transversal de la matriz, surgen esfuerzos mayores en la interfaz matriz-pieza en bruto, porque existe un aumento de las presiones de contacto en dicha área.
De la misma forma, el aumento del ángulo de la matriz provoca que el desgaste sea mayor en la herramienta, pues un ángulo obtuso dificulta la salida del material, lo que conduce a un aumento significativo de las presiones de contacto en la interfaz matriz-pieza en bruto; por tanto, de acuerdo con el modelo de desgaste de Archard, este fenómeno se intensificará.
Un resultado interesante es la influencia del coeficiente de fricción sobre el desgaste, pues se evidencia que a medida que este aumenta, el desgaste disminuye, lo cual coincide con lo planteado en el modelo de desgaste de Archard. La velocidad de deslizamiento se disminuye por el aumento de la fricción (resistencia al movimiento), al mantenerse constante la velocidad de extrusión.
De este modo, una alta fricción provocará un menor desgaste, pues al aumentar esta sin producirse un aumento proporcional de la velocidad de extrusión se genera una ralentización del proceso, por lo que no se alcanza la velocidad de deslizamiento necesaria para que ocurran pérdidas de material (desgaste). Estos resultados son concordantes con lo planteado por Lepadatu et al. (2006) quienes de igual manera demuestran que el aumento del coeficiente de fricción disminuye el desgaste en la matriz de extrusión, al mantenerse constante la velocidad de deslizamiento entre los componentes. Asimismo, Zhang et al. (1997) declaran que en un régimen de desgaste, al incrementarse la velocidad de deslizamiento (lo cual implica una disminución del coeficiente de fricción) se evidencia un aumento en la intensidad del desgaste, dichas consideraciones fueron tomadas a partir de los ensayos experimentales realizados en aleaciones de aluminio 6061.
Lo anteriormente explicado evidencia la necesidad del uso constante de lubricantes en estas operaciones, ya que el mismo contribuye a disminuir la presión normal de contacto entre las superficies y por consiguiente el desgaste.
Modelo matemático para establecer la intensidad del desgaste en la matriz de extrusión a partir de la simulación numérica
La ecuación (8) describe el comportamiento de los principales factores que inciden en el desgaste (Wp) de la matriz de extrusión, según la simulación por el MEF, teniendo en cuenta las condiciones de funcionamiento descritas anteriormente.
La Figura 8 muestra la relación lineal que existe entre tres de los factores más significativos, determinados en esta investigación, que influyen sobre la intensidad del desgaste de la matriz de extrusión directa de aleaciones de aluminio 6061-O, lógicamente los valores negativos se desechan.
Conclusiones
La implementación del modelo de desgaste de Archard en las simulaciones mediante el MEF del fenómeno del desgaste evidenció la influencia de las propiedades geométricas de la matriz de extrusión siendo la ZIP el área más crítica, lo cual coincide con lo planteado en la literatura especializada.
El DPB permitió determinar los factores que más inciden en el desgaste de la matriz y son: la razón de extrusión, el coeficiente de fricción, el ángulo de incidencia y en menor medida la longitud del apoyo de la entrada y el radio de entrada 1.
El modelo matemático lineal obtenido permite una evaluación del fenómeno del desgaste, a partir de los parámetros geométricos de la matriz de extrusión, lo que facilita la toma de decisiones en las etapas de diseño y fabricación de la herramienta de conformado atendiendo al comportamiento de dicho fenómeno.











 nueva página del texto (beta)
nueva página del texto (beta)








