1. Background

It is widely known that the development of problem - solving skills is an important issue in formal education. In fact, authors such as ^{Lazakidou and Retalis (2010)} linked it to Life - long Learning in the sense that "engagement in problem - solving activities helps students to acquire useful attitudes such as thinking, flexibility, creativity, and productivity, which are very important to real life " (p. 3). In the current educational context, mathematical problem solving takes a greater relevance; this activity, which starts in the first years of Elementary Education, may be the basis to develop basic problem - solving skills.

Mathematical problem solving is a complex cognitive activity that involves multiple processes. A student's achievement in these tasks relies on the integrated application of cognitive, metacognitive, and motivational components (^{Cleary & Chen, 2009}; ^{Kajamies, Vauras, & Kinnunen, 2010}; ^{Montague, Enders, & Dietz, 2011}; ^{Voyer, 2011}). In fact, while it has been supported for many years that a well - organized and flexibly accessible knowledge about mathematical facts, symbols, algorithms, concepts and rules may be the core of problem - solving skills, current literature has established that strategy use based on Self - regulated Learning (SRL) is linked to mathematical capacities which are an important determining factor in solving mathematical problems (^{Gálvez, Cosmelli, Cubillos et al., 2011}; ^{Geary, 2004}; ^{Jarero, Aparicio y, Sosa, 2013}; ^{Lazakidou & Retalis, 2010}; ^{Montague, 2008}; ^{Pennequin, Sorel, Nanty, & Fontaine, 2010}; ^{Pereis, Dignath, & Schmitz, 2009}; ^{Schmitz & Perel, 2011}; ^{Verschaffel, Greer, & De Corte, 2000}).

SRL refers to those proactively initiated thoughts, feelings and behaviors which are planned and cyclically adapted based on self - generated or performance feedback in order to attain personal goals (^{Zimmerman, 2000}). SRL involves those aspects which facilitate the control and regulation of students' cognitive systems and learning processes, and comprises three sequential phases: forethought (i.e., processes that precede efforts to learn or perform), performance control (i.e., processes occurring during learning efforts), and self - reflection (i.e., processes occurring after learning or performance such as evaluate the effectiveness of one's learning methods or results; ^{Zimmerman, 2000}; in ^{Cleary & Chen, 2009}). These processes, which are based on an interplay of personal and task characteristics and the strategies available in a learning situation, help students to monitor and check their thoughts and are particularly useful when solving novel or challenging problems (^{Lazakidou & Retalis, 2010}; ^{Pennequin et al., 2010}; ^{Rosenzweig, Krawec, & Montague, 2011}; ^{Throndsen, 2011}; ^{Zimmerman & Schunk, 2008}). However, studies have shown that students tend to demonstrate poor metacognitive skills when they are engaged in mathematical problem - solving situations. Many students forge ahead without considering alternative decisions, jumping immediately into calculations, giving impulsive reponses, and using trial and error as strategies. Students often get stuck in irrelevant details of the task or fail to verify solution paths and evaluate answers, focusing on superficial measures of progress (^{Cleary & Chen, 2009}; ^{Kramarski & Gutman, 2006}; ^{Montague, 2008}; ^{Montague et al., 2011}; ^{Pennequin et al, 2010}; ^{Pereis et al., 2009}; ^{Veenman, 2005}). In this sense, not only do students with learning disabilities show problems in these issues. In fact, typical students may also not realize the importance of regulating their thoughts and behavior, or they may simply not know how to self - regulate properly. Thus, many students often need support to regulate their learning processes (^{Azevedo & Cromley, 2004}; ^{Butler & Cartier 2005}; ^{Ifenthaler, 2012}; ^{Kramaski & Gutman, 2006}).

In this context, one of the biggest challenges for researchers is to design measures that provide access to internal cognitive structures and functions involved in both, self - regulation and problem solving. Most studies have been based on applying standardized measures such as questionnaires or structured interviews; this kind of measures involves asking students about how they solve a problem or the extent to which they use different strategies. Additionally, students are also asked about different situations in which they would use (or not use) a specific strategy or what approximation would be the best in each case. Students' responses to the metacognitive questions are scored depending on the quality of the response and a total score is calculated. These kind of assessments, although widely applied (^{Greene & Azevedo, 2010}; ^{Shea & Bidjerano, 2010}; ^{Zimmerman & Schunk, 2008}), may yield inconsistent or inaccurate information due to inaccurate memory or perhaps even response biases such as social desirability, and do not provide information about how learners transfer their knowledge to regulate their problem - solving activities. As many authors have pointed out, these tools are useful to assess a student's declarative and situational metacognitive knowledge, but do not provide any information about the mental processes underlying task performance and the student's achievement levels which together represent important issues in learning and instruction (^{Clearly & Chan, 2006}; ^{Veenman, 2011}). In response to this, ^{Veenman (2011)} established the distinction between off-line and on-line methods in the assessment of strategy use and learning. Off-line methods refer to questionnaires and interviews which are administered either before or after task performance, while on-line methods concern measurements taken concurrent to task performance, such as Think - aloud or Triple Task procedures. These measures may be especially useful to provide data about student reasoning abilities during problem - solving activities.

In Think - aloud protocols (^{Rosenzweig et al., 2011}) learners verbalize their thoughts and cognitive activities while engaged in task execution. The usefulness of these procedures lie in the fact that they provide access to students' short-term memory abilities, which reflects cognitive processing during task completion. This approach allows the researcher to obtain accurate information about metacognitive skills and strategies while students are asked to simply verbalize what they are thinking at each moment. After transcription and coding, undirected verbalizations are recognized as valid expressions of the students' cognitive and metacognitive processes. Studies in this area are limited, although some interesting data support the usefulness of the protocols in assessing metacognitive processes during mathematical problem-solving tasks (^{Lazakidou & Retalis, 2010}; ^{Ostad & Sorenson, 2007}; ^{Throndsen, 2011}).

On the other hand, Triple Task procedures have been widely applied in the scientific study of reading comprehension and written composition, and more recently in note - taking activities (^{Fidalgo, Torrance, Robledo, y García, 2009}; ^{García, Rodríguez, Pacheco, & Diez, 2009}; ^{Piolat, Barbier, & Roussey, 2008}; ^{Piolat, Kellog, & Farioli, 2001}; ^{Olive et al., 2002}; ^{Piolat & Olive, 2000}; ^{Piolat, Olive, & Kellogg, 2005}; ^{Torrance & Galbraith, 2006}).

The Triple Task method is rooted in the so-called "Doble Task " protocols. Although the present study focuses on the use of Triple Task procedures, a description of both methods is provided below:

The Double Task procedure provides information about the cognitive effort engaged in higher - order cognitive tasks, such as comprehension or text production. Participants are asked to perform concurrently a primary task and a secondary probe task. For example, while composing a text (the primary task), participants must react as fast as possible to tones (the secondary task by pressing a mouse button or by saying 'stop' to a microphone linked to a vocal key) that are periodically distributed in a random interval (generally between 15 and 45s). Reaction time (RT) in this dual - task situation is compared with a control condition when the probe is responded to as a single task. The degree of interference in RT (IRT) caused by the primary task provides a measure of the amount of cognitive effort designated to composition or another cognitive task. However, although widely used, this measure does not provide information about the process that underlies the cognitive task under consideration.

It is the Triple Task procedure which provides additional information about the temporal organization and the cognitive processes underlying a cognitive activity by adding a third task, consisting of asking students for an immediate directed introspection after each tone's detection. Students have to categorize their thoughts at the moment the tone is presented. Thus, in Triple Task studies students perform: a) the primary task under investigation, b) the secondary probe task, and c) a third task in which participants are asked to label the process that was interrupted by the probe. For this last task, participants are trained in direct retrospection in order to better identify and report the cognitive processes present at each moment. As a measure of the process, the Triple Task method can be differentiated from Think - aloud protocols in the following aspects: a) the Triple Task uses directed introspection as opposed to the undirected introspection involved in Think - aloud, b) a system of categories can be given in order to facilitate categorization and facilitate exploration in to sub-processes, c) response transcription and coding are unnecessary, and d) inter-rater agreement does not have to be calculated. To date however, this method has neither been applied to the analysis of the processes underlying mathematical problem - solving, nor from the point of view of investigating the metacognitive skills involved in these tasks. Additionally, as happens with Think - aloud protocols, most Triple Task studies have been conducted with small sample sizes, mainly due to their own methodology feautures, which make them less economic to implement.

In this context, we introduce our own process assessment tool, the Triple Task Procedure in Mathematics - TTPM (^{García y González - Pienda, 2012}). It is based on the Triple Task technique and suitable for application in larger samples through a MOODLE platform. One of the novelties of this method is the introduction of a new system of categories to analyze student processes during problem solving. It was designed according to the PLEJE model of SRL ("Planificación - Ejecución - Evaluación" in Spanish: ^{Rosário, Mourão, Núñez, González - Pienda, & Solano, 2008}; ^{Zimmerman, 2000}), which establishes three main phases: Planning, Execution, and Revision; and ^{Bransford and Stein's (1993)} IDEAL problem - solving model, which stablishes five stages to successfully solve a problem: Identifying potential problems, Defining and representing the problem, Exploring possible strategies, Acting on those strategies, and Looking back and evaluating the effects of those activities. A more detailed description of the assessment process and this tool, which was administered to 510 students from fifth and sixth grade belonging to 12 private and state schools in Asturias (Northern Spain), is provided in the method section. The main aim of this study was to analyze the usefulness of TTPM as a measure of the process during the performance of two mathematical problems of varying difficulty. Specifically, this study sought to answer the following questions: a) do students follow Self - Regulated Learning stages while trying to solve mathematical problems? b) are there differences in the process followed by students with different achievement in the tasks? and c) do these differences remain constant when the difficulty of the tasks varies?

2. Method

2.2. Measures

Mathematical problems: Students completed two relatively complex mathematical word problems taken from the book "Problem - solving and comprehension" (^{Whimbey & Lochhead, 1999}) published in Spanish. This book provides a systematic review of the characteristics that define a good problem solver, while proposing strategies and activities to develop these skills, mainly based on mathematical reasoning. Tasks differ in the amount of information to be processed, the number of associations presented and the number of parameters to calculate.

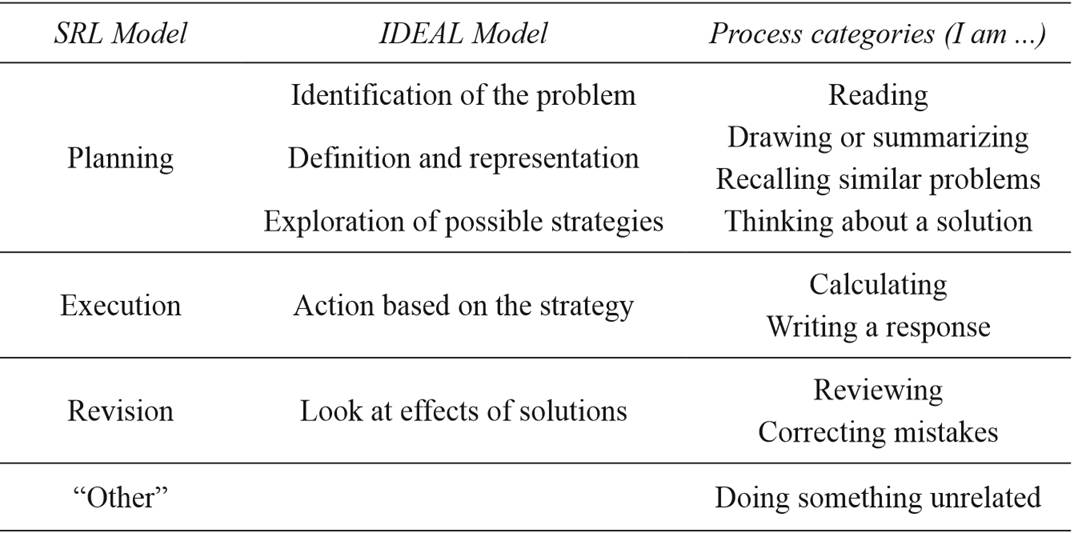
Process measures: Evidence of student metacognitive process was obtained by means of the TTPM (^{García y González - Pienda, 2012}). It consists in the following: after a RT probe task, and while completing the mathematical problems, students are presented with an electronic tone at a randomized interval of 40-45 seconds. At this point students are asked to categorize their activities or thoughts. In order to help students, categorize these processes, students are provided with a category system (see Table I). They have to indicate by mouse - click which of nine the categories (reading, drawing or summarizing, recalling similar problems, thinking about a solution, mental calculation, writing, reviewing, correcting mistakes, or "other") best describes the processes in which they are involved when the tone is presented. The category system is based on ^{Bransford and Stein's (1993)} IDEAL problem - solving model and the PLEJE model of SRL (^{Rosário et al., 2008}; ^{Zimmerman, 2000}), previously described in this study. The category called "other" was incorporated to gather all those thoughts or actions unrelated to the mathematical task (e.g., day - dreaming). Nevertheless, previous research indicates that such unrelated processes are generally very scarce (^{Olive et al., 2002}). The eight proposed processes are also organized into three, higher - level categories corresponding to SRL phases: Planning, Execution and Revision. Table I shows the category system used for students to categorize their processes during the task, based on the correspondence between the stages and phases involved in both SRL and IDEAL models.

Table I Category system. Based on the Self - Regulation Model (^{Rosário et al., 2008}; ^{Zimmerman, 2000}) and the IDEAL Model (^{Bransford & Stein, 1993}) 

3. Results

3.1. Student problem - solving process

In order to demonstrate if a student's problem-solving process responds to SRL phases, Figure 1 shows the profile of the process followed by students in Tasks 1 and 2. This profile indicates similar processes for both tasks, characterized by a higher frequency of selected categories in planning and execution phases. The means (Table II) indicated a percentage of 49.46% in Task 1 and 45.53% in Task 2 of the students' reports referring to planning categories, while those related to execution were 40.43% and 45.95%, respectively. With respect to the revision phase, mean percentages of categories reported within this phase were 10.15% in Task 1 and 7.57% in Task 2 across categories. It must be noted in this case the high means found in the planning phase (even above those found in the execution phase). This is because the planning phase consists of four sub-processes or categories, while the other phases comprise two.

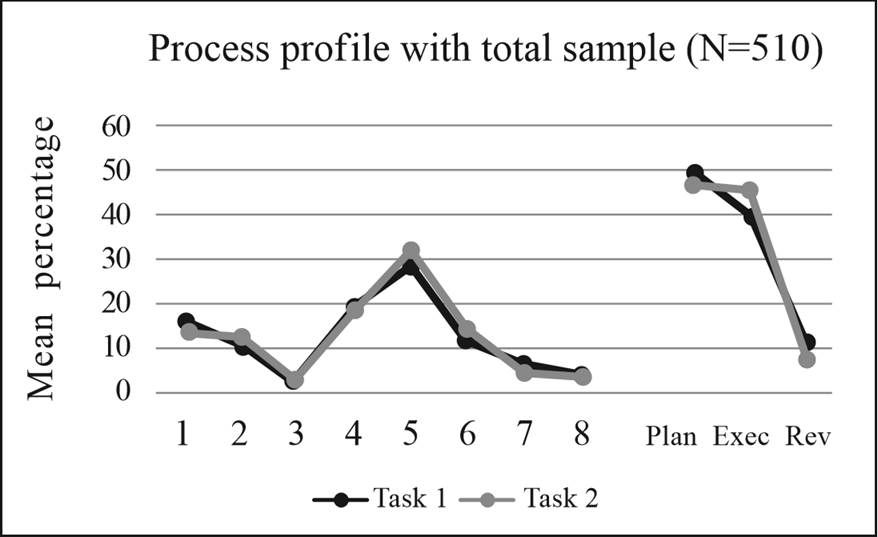
Figura 1 Process profile of the total sample. Tasks 1 and 2.1 = reading; 2 = Drawing or summarizing; 3 = recalling similar problems; 4 = thinking about solutions; 5 = mental calculation; 6 = writing; 7 = reviewing; 8 = Correcting mistakes; Plan = planning phase; Exec = execution phase; Rev = revision phase 

In respect to the categories or sub-processes within each phase, in the planning phase "thinking about solutions" and "reading" were the most frequently reported categories, with mean percentages of 19.20% in Task 1 and 17.02% in Task 2 for the first category, and 15.98% and 13.57% respectively for the second category. "Recalling similar problems" was the least reported category or sub-process, although higher in the second task (2.97% in Task 1 and 6.67% in Task 2). "Drawing or summarizing" represented 11.29% of the total categories reported in Task 1 and 12.36% in Task 2, being an important sub-process within planning. With respect to execution phase, "mental calculation" was the category most frequently reported in this phase, with mean percentages of 28.37% in Task 1 and 31.83% in Task 2. "Writing" also represented an important percentage of the categories used, with a 12.09% frequency reported in Task 1, and 14.14% in Task 2. In relation to the revision phase, "reviewing" and "correcting mistakes" were two of the least frequently reported categories by students in both tasks (6.36% in Task 1 and 4.29% in Task 2 for "reviewing"; 3.79% and 3.29 respectively for "correcting mistakes").

Finally, standard deviations in Table II showed a high variability among the processes shown by students in both tasks, mainly in the categories less reported ("recalling similar problems", "reviewing" and "correcting mistakes").

Table II Means and Standard Deviations in process variables. Total sample (N=510). Tasks 1 and 2. 

3.2. Process differences between groups with different achievement (success / failure)

Tables III and IV present the mean scores and standard deviations in process variables for groups with different achievement (Group 1 = success; Group 2 = failure) in Tasks 1 and 2, respectively. Group - compositions revealed the presence of a high proportion of students solving the mathematical problems unsuccessfully. Specifically, 356 students (69.80%) failed to solve the first task while 327 students (60.11%) gave an incorrect answer on the second task. As one of the aims of this study was to know whether there were differences between tasks with varying difficulty, separate analyses for each task were conducted.

For the first task, means in Table III indicated a trend to plan more, and to execute and review less, in the Group 1 (success). MANCOVA analyses showed the presence of statistically significant differences between the groups (λ = .957; F _(11,496) = 2.012; p =.026; ηp ² = .043). However, these differences were only found in "drawing or summarizing" (F _(1,506) = 4.548; p = .033; ηp ² = .009). As happened with planning, this sub-process was more frequently reported by students who successfully solved the task. Gender and grade level, which were included as covariates, did not generate any differences in the process (p = .461 and p = .123, respectively).

Table III Means and Standard Deviations in process variables for each group. Task 1 

With respect to the second task, the means in Table IV showed a different pattern of results, with students who successfully solved the problem reporting using less sub-processes related to planning, and more related to the execution and revision phases. MANCOVA analyses indicated the presence of statistically significant differences between groups (λ = .951; F _(11,496) = 2.303; p = .009; ηp ² = .049). These differences were found in those categories or sub-processes within the planning phase: "reading" (F _(11,506) = 5.499; p = .019; ηp ² = .011), "drawing or summarizing" (F_(11,506) = 4.604; p = .032; ηp ² = .009), "recalling similar problems" (F _(11,506) = 5.209; p = .023; ηp ² = .010) and "thinking about solutions" (F _(11,506) = 5.387; p = .021; ηp ² = .011). Differences in the planning phase were close to statistical significance (F _(11,506) = 3.825; p = .051; ηp ² = .006). Means revealed that students who successfully solved the task (Group 1) reported reading, recalling similar problems, and thinking about solutions less frequently than the other group. As with the first task, successful students also reported using representation strategies (i.e., drawing or summarizing) more frequently than their peers. Gender and level did not generate differences in the process (p = .590 and p = .230, respectively).

Table IV Means and Standard Deviations in process variables for each group. Task 2 

4. Discussion and conclusions

It has been argued that it is essential to identify economic, fast, reliable, and valid techniques to elicit and analyse cognitive processes involved in different cognitive tasks (^{Ifenthaler, 2008}; ^{Ifenthaler, Masduki, & Seel, 2011}). In this context, the main aim of this study was to analyse the usefulness of a new assessment tool based on the Triple Task procedure and designed to assess the metacognitive and self - regulated processes shown by the 510 fifth and sixth grade students during the performance of two mathematical problems of varying difficulty. Specifically, this study tried to answer these questions:

Do students follow Self - Regulated Learning stages while they try to solve mathematical problems? Global results indicated the presence of important differences among processes followed by students, as indicated by the high standard deviations. This variability was even higher in the categories or sub-processes less frequently reported by students in general: recalling similar problems, reviewing and correcting mistakes. The pattern of results was similar in both tasks, and was characterized by a lack of evaluation strategies. However, sub-processes related to Planning and Execution phases were the most frequently reported, respectively. These result may seem to contradict some previous research pointing out that student commonly tend to be impulsive in problem - solving situations, spending little time making a plan to develop (^{Cleary & Chen, 2009}; ^{Kramarski & Gutman, 2006}; ^{Montague, 2008}; ^{Montague et al., 2011}; ^{Pennequin et al, 2010}; ^{Pereis et al., 2009}).

However, despite the fact that these results could indicate that once students properly planned an activity, making mistakes became less likely and reviewing activities less necessary, students' achievements in both tasks revealed a high proportion of failure. This indicated that planning strategies were not effective enough. In fact, an analysis of the sub-processes involved in the planning phase revealed that thinking about solutions and reading were the most frequently reported sub-processes within planning, while the use of potentially more useful strategies such as information representation and organization were less frequent among students. This result could indicate a trend to use passive solving strategies or even comprehension difficulties.

Are there differences in the processes followed by students with different achievements in the tasks? Analyses revealed the existence of statistically significant differences between groups. These differences were located in the subprocess of drawing or summarizing in Problem 1, while significant differences were found in all the sub-process within the planning phase in Problem 2. The existence of more significant differences in this second problem could be related to its characteristics (i.e., more complex relationships to stablish, parameters to calculate, etc.). Thus, this task may result more difficult, suggesting a more important role of planning strategies when problem difficulty and demands increase. Regarding the pattern of differences, students who successfully solved the tasks tended to draw and summarize more, but they recalled similar problems, read and thought about solutions proportionally less than those who failed to solve the tasks. These results are consistent with the statement above about the effectiveness of planning strategies, and suggest the use of more active processes by students with high achievement. In this sense, the strategy that showed to be effective in both tasks was drawing or summarizing (i.e. using information representation and organization strategies). Making this kind of representations would correspond to the "translation" process, characterized as an essential part of solving mathematical problems by many authors (^{Abdullah, Zakaria, & Halim, 2012}; ^{Csíkos, Szitányi, & Keleme, 2012}; ^{Díez-Palomar, Menéndez, & Civil, 2011}; ^{Pantziara, Gagatsis, & Elia, 2009}; ^{Stylianou, 2011}). An example of graphical representation, made by a participant in this study, is shown in Figure 2.

Figura 2 Example of students' answers in the second task 

The use of graphic representations supposses an important part of planning strategies. As ^{Montague and others (2011, p. 263)} argued, "problem representation involves translating and transforming linguistic and numerical information into verbal, graphic, symbolic, and quantitative representations that show the relationships among the problem parts prior to generating appropriate mathematical equations or algorithms for problem solution" . In fact, ^{Abdullah and others (2012)} showed in their study that when the teaching approaches encourage students to apply thinking strategies through using visual representation, students are able to gain a better conceptual understanding and eventually improve their mathematics achievement. They attributed this effect to a more active involvement of students in their learning process. However, representation is not only a matter of copying what one sees. As the example above shows, it involves a process of personal re-organization, inventing or adapting conventions of a representational system for the purpose at hand (^{Stylianou, 2011}).

Are there differences between tasks with varying difficulty? Although differences in the main phases of planning, execution and review were not statistically significant, analyses revealed the existence of significant differences in the sub-process involved in planning, separately. In this way, differences in the metacognitive process showed by the groups with different achievement were stronger in Task 2, which implied more relationships to stablish and maybe more complex. This would initially suggest a more important role of planning strategies when task difficulty and demands increase.

In summary, the results found in this study would seem to contradict those studies that indicated that students do not plan, jumping immediately to calculations without considering alternatives to solve problems or giving impulsive responses (^{Cleary & Chen, 2009}; ^{Kajamies et al., 2010}; ^{Kramaski & Gutman, 2006}). In fact, students in this study reported having planned. However, an in-depth analysis of the sub-process involved in planning revealed the presence of ineffective planning strategies implemented by the overall group, which was translated into a greater percentage of failure in both problems. In this sense, another important finding of this study is that students had serious difficulties to evaluate their progress. They also showed a tendency to use familiar procedures, such as performing calculations, as a method to solve the problems. Thus, students in this study did not self - regulate or implement effective metacognitions during problem solving. However, differences between groups with different achievement levels suggested that, despite the fact that students did not show a properly self - regulated process, a proportion of them were able to use more effective and active strategies while solving the problems, such as organizing or representing the information. This is in fact an important determinining factor in successful mathematical problem solving. Finally, the use of effective planning strategies seemed to be most important when the task difficulty and demands are greater.

These findings add evidence to the utility of process measures, specifically those based on directed and concurrent self - reporting, in the assessment of cognitive activities (in this case mathematical problem - solving tasks). The usefulness of the assessment tools presented in this studylies, however, in the systems of categories designed, which makes it possible to divide mathematical problem - solving tasks into sub-processes or isolated activities, and provides in-depth insights about a student's strengths or weaknesses, thereby helping to understand their success or failure from the point of view of SRL. This is not only important for instruction, but specially for student learning. In this sense, as ^{Ifenthaler (2012)} pointed out, the key link between knowledge about (and the regulation of) one's own problem - solving activities may lie in reflective thinking. Making students aware of their own learning processes may help them generate information about the efficiency of their problem-solving strategies and successfully implement that knowledge in the ongoing problem-solving process, thereby being able to control and regulate their cognition, effort and behavior.

It is necessary to acknowledge, however, the following limitations in the present study: first, as self - regulation is a cyclical process (^{Zimmerman, 2000}), analyzing the recursion of the process followed by students may bring useful information about its temporal course and the metacognitive mechanisms involved. In this sense, identifying different patterns of performance may also help to reduce the high variability whithing - subjets found in this study; second, motivational and affective components, such as self - efficacy beliefs, task interest and perceived instrumentality, have been demonstrated to play an important role in mathematical performance and problem solving situations (^{Ahmed, Minnaert, Kuyper, & Van der Werf, 2012}; ^{Cueli, García y González - Castro, 2013}; ^{Dettmers et al. 2011}; ^{Hoffman, 2010}). The study conducted by ^{Ahmed et al. (2012)} revealed that a good students' performance in addition and subtraction tasks was related not only to the student's use of advanced mathematics strategies and SRL competence, but also to the ability attribution for success, effort attribution for failure, and high perceived self - efficacy when using specific strategies; third, it would be interesting to extend the number of mathematical problems, also adding different levels of difficulty, which would provide more accurate information about the influence of task difficulty in problem - solving processes; additionally, in order to provide support to the usefulness of the tool applied in this study as a measure of self - regulatory processes involved in mathematical problem solving, analyzing its relationship with other standardized instruments such as questionnaires and interviews would be useful. Complementary use of both measures would provide a better understanding of self - regulatory mechanisms exhibited by the students, thus helping to design more adapted instructional strategies; finally, and given the characteristics of the sample (students belonged to different schools in a specific area in Northern Spain), extending the research to other areas would be advisable in order to better stablish the scope of the findings. This is, however, the first approach to the study of the usefulness of the Triple Task technique in the assessment of the process involved in solving mathematical problems. Therefore, the results from the present study actually open the way for future research. In this sense, it would be interesting, for example, to conduct multi - level modeling that would take in to account school level effects.