1. Introduction

Ultrasound systems have been widely used for image analysis in areas such as obstetrics, gynaecology, and veterinary medicine. They have shown advantages like working in real time and being non-invasive, portable, and with lower costs than other imaging modalities such as magnetic resonance or computed tomography. However, ultrasound images present multiplicative noise, acoustic shadows, poorly defined edges, and the transducer can be altered by external variables, which results in an inadequate image acquisition (^{Contreras-Ortiz et al., 2012}). Weigang et aI. report that damage to individual transducer elements within an array affects the overall ultrasound probe performance (Weigang et al., 2020). All these alterations highlight the need to calibrate ultrasound equipment with a known model or phantom. This is important to achieve good quality images with correct spatial dimensions (^{Mercier et al., 2005}). In this context, the good quality of images refers to preserving the spatial dimensions of the acquired object, attenuating acoustic shadows derived from high impedance and thus having more homogeneous gray scale intensity values, as well as well-defined edges.

Phantoms for testing ultrasound equipment find applications both in academic research and clinical diagnosis. They have been useful for the implementation of experimental protocols, in the analysis and simulation of materials (^{Sun et al., 2010}), for testing measurements, and calibration of transducers (^{Vogt et al., 2017}). This entails a great responsibility that makes it necessary to count with a calibration stage. According to the Centro Nacional de Metrología (CENAM) for a measurement to be trustworthy it must be referred to a standard (^{CENAM, 2020}). That is the reason why relying on a phantom with specifications suited to a calibration standard would give greater certainty not only to experimental results but also to clinical diagnosis.

Phantoms are widely used for training medical personnel and calibrating of ultrasound devices. Phantoms must be durable and have properties that, among other physical properties, allow waves to travel and return to the source (^{Cournane et al., 2012}). Additive manufacturing or 3D printing is a sequential superposition of materials controlled by a computer to create three-dimensional shapes. This method is being considered as an alternative to produce the phantom prototypes not only for its low cost but also for its versatility for building highly complex structures (^{Wood et al., 2017}). As a previous step for manufacturing prototypes, it is convenient to mathematically model them to find what design parameters to optimize. For example, they must have a global or effective behavior such that their acoustic impedance is low (close to tissue, approximately 1.5 Mrayl) to avoid loss of energy at the transducer-prototype interface (^{Smith & Auld, 1991}). Also, phantoms must present an average (i.e., nor to large neither to low) attenuation coefficient that allows the wave to travel and not fade away (like Water, Human tissue, Silicone, PVA (polyvinyl alcohol) or PAA (Polyacrylamide gel)) (^{Zell et al., 2007}). The interaction between curvilinear transducers and curved surfaces presents lower measurement errors compared to linear transducers and curved surfaces (^{Cikes et al., 2019}). Therefore, a curvilinear transducer can be better coupled to geometries like those describing human or animal organs which are mainly curved (^{Warner et al., 2008}).

To imitate the heterogeneous structure of human tissue, phantoms are typically formed by tissue analogues embedded in a matrix, made of gelatin or agar. Hence, there are many design parameters to account for when designing phantoms, for example: the volume fractions of the analogues, their physical properties, and geometric shapes. A suitable conjunction of these parameters is sought that the final product has effective or macroscopic properties that are close to the acoustic impedance and attenuation coefficients of human tissue.

A composite material is a heterogeneous material constituted of alternating volumes of some homogeneous materials at the supramolecular scale (^{Panasenko, 2008}). The main objective of this work is to propose a methodology that allows to balance effective impedance and attenuation to seek from a given class of composite materials (phantoms). We are interested in those that combine a low acoustic impedance with an average attenuation coefficient (like water). To determine such effective properties, the proposal is based on mathematical homogenization methods of composite materials. Homogenization methods allow the study of a composite material to be substituted for a homogeneous material whose properties depend on the physical and geometric characteristics of its constituents. Panasenko offers a very instructive rundown of the mathematical techniques of homogenization with classic references (^{Panasenko, 2008}). A recent review on composite materials with applications in biomedical engineering appears in (^{Egbo, 2020}).

In this contribution, for simplicity, we work with sandwich-type structures to illustrate a general design scheme of phantom composites for the calibration of ultrasound equipment. However, the theory and methods of analysis of these structures have a great potential in biomedical applications as well as in the characterization of bones and tissues (^{Birman & Kardomateas, 2018}).

The rest of the contribution is continuous as follows. In Section 2, a methodological scheme is illustrated with a simple model of a sandwich phantom made on agar with different concentrations. In Section 3, numerical examples are presented and the criteria for design are discussed. Finally, some concluding remarks are given.

2. Materials and methods

In this section, a methodology is described for modeling a simple sandwich composite made of Agar with different densities. Agar is a useful material for the construction of phantoms for ultrasound training. It does not require refrigeration. Resists melting and deterioration. It can be reused. (^{Earle et al., 2016}). Other materials as PVA and HNT (halloysite nanotubes) have been used for various biomedical applications. The methodology here described can also be extended for phantom-composite made of PVA-HNT. A review on properties and applications of PVA-HNT composites can be found in (^{Gaaz et al., 2015}). Each layer of the sandwich is assumed to be linear with complex elastic moduli, isotropic and homogeneous material. The aim is to estimate a variation range for the layers’ dimensionless thickness or volume fraction, θ (Figure 1), to obtain a macroscopic response that guarantees a low acoustic impedance and an average wave attenuation. The procedure is presented by an example that suggests the best combination according to the parameters selected for the design.

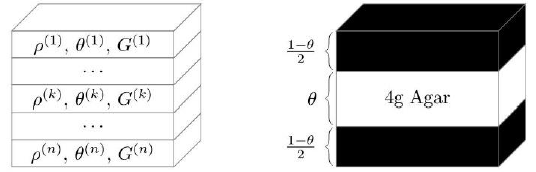
Figure 1 Model of a laminate composite phantom with n layers (left). The sandwich-like numerical example with three layers (right). 

Let us consider the complex elastic modulus G=Gr+iGi, where Gr and Gi denote its real and imaginary parts, respectively. The real part is associated with energy storage and the imaginary part, to energy losses (^{Manickam et al., 2014}). In a homogeneous material, the elastic moduli Gr and Gi, and the mass density ρ, can be calculated by using the following formulas:

where z, v, α and f are the acoustic impedance, sound speed, attenuation coefficient and the frequency, respectively.

The third Formula in (1) is an approximation proposed by ^{Hartmann (1990)}. The inverses of the formulae above give the acoustic impedance, sound speed and attenuation coefficient as functions of the moduli, frequency, and density:

In the case of a heterogeneous material, like a composite phantom, the real and imaginary parts of the elastic modulus that appear on the Formulae (1.1) are the effective ones which depend on the moduli and volume fractions of each component. That dependence on those design parameters is the one that will be explored in the present section.

To calculate these effective properties, we applied mathematical homogenization to the model laminate composite that is shown on the left of Figure 1. Each layer represents a different component of the material, various tissue analogues or the binding material between them. The i-th layer has complex elastic modulus G(i), density ρ(i) and dimensionless thickness θ(i). The total thickness of the material is unitary: ∑i=1nθ(i)=1.

In the case of a laminate, the effective values of the real G-r and imaginary G-i parts of the elastic modulus may be found, for instance, through the Formulae (41) of (^{Bravo-Castillero et al., 2020}) that take the following form in the present notation:

where a denotes the average of the property a weighted by the dimensionless thicknesses θ(i), that is: a= ∑i=1nθ(i)a(i).

The Formulas in (2) can be used for any finite number of layers, but we are going to illustrate their implementation with only three of them as it is shown to the right of Figure 1. The concentration of the center layer of the sandwich-like phantom is fixed at 4g and its dimensionless thickness is θ. In this case the averages of Formulae (2) adopt the form:

where the superscript in parenthesis indicates the concentration of the layer (center: 4g; top and bottom: x. The parameters that we are going to explore in the Results section of this preliminary study are the thickness of the center layer θ and the moduli of the top and bottom layers.

3. Results

In Table 1, the raw data that was used for the calculations is shown. It consists of impedance, sound speed and attenuation for Agar of different concentrations and human tissue. To find the complex moduli that serves as input of Formulae (2) we need to first use Formulae (1). The results shown in this study illustrate the behavior of acoustic impedance and attenuation at a fixed frequency of f=5×106Hz.

In Figure 2 the real and imaginary parts of the effective elastic modulus for different concentrations of Agar are shown. The implementation of the analytical formulae is validated by a good agreement with the FFT-based method (the highest relative error between the two is around 0.2%). The results from numerical homogenization are only plotted for a few dimensionless thicknesses of the 4g Agar center layer because of its relatively higher computational cost. To produce each of the points, it is required the convergence of a fixed-point iteration (^{Moulinec & Suquet, 1998}). This makes it less suitable for an exploration of design parameters. On the other hand, calculations via the formulae are straight-forward. This difference in computational cost in favor of the analytical methods is even larger for other geometries of the phantoms (non-laminates).

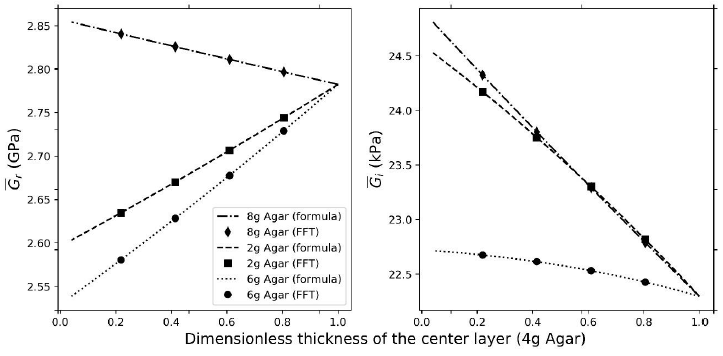
Figure 2 Real (left panel) and imaginary (right panel) parts of the effective complex elastic modulus vs. the dimensionless thickness of the center layer calculated via the Formulae (2) and the FFT-based numerical method for different concentrations of Agar. 

In Figure 2, the curves converge when the volume fraction of 4g Agar is equal to 1 or, equivalently, when θ = 1 in the Formulae (3). The lines converge because when θ = 1 the phantom is solely composed by the center layer.

Once the composite has been homogenized, the Formulas (1.1) for homogeneous materials can be used to calculate the effective acoustic impedance z-, and the effective attenuation coefficient α-, as functions of the dimensionless thickness θ of 4g Agar (shown in Figure 3). In this preliminary study we will focus on the low impedance and average attenuation coefficient criteria for selecting design parameters of a composite phantom. The curves describe the behavior of these parameters in three sandwich composites of the “Xg/4g/Xg” type (with the same density of 4g of Agar in the central layer), whereas in the top and bottom layers possess Xg(= 2g (dashed line),= 6g (dotted line), and = 8g (dash-dotted line), respectively) of Agar density. A visual inspection of the curves of Figure 3, a laminate with the top and bottom layers of 6g Agar would have, simultaneously, the lowest z- and intermediate values α-, among the available materials, for all values of θ. In this particular selection of materials, any dimensionless thickness of the center layer (4g) satisfies the criteria for top and bottom layers of 6g Agar. In this way, we can conclude from the three combinations studied that the 6g/4g/6g composite sandwich is the one that best meets the design requirements to be used in the calibration of ultrasound equipment.

Figure 3 Effective impedance and attenuation as functions of the dimensionless thickness of the center layer for different concentrations of Agar and for human tissue. 

4. Conclusions

Ultrasound equipment calibration with well-manufactured prototypes is important to acquire good quality images, which include defined contours, correct spatial dimensions, and a higher signal-to-noise ratio. A well-calibrated ultrasound system allows a proper measurement in image analysis, which is crucial in medical or veterinary applications.

In this preliminary study, a simple example is analyzed in order to show a general modeling methodology for composite materials that could be used as prototypes for calibration of ultrasound devices. A design criterion that involves both low acoustic impedance and average attenuation coefficient was proposed and described.

This work represents an application of composite material mechanics to a biomedical engineering problem. In such problems it is necessary to find relevant parameters (acoustic impedance and attenuation coefficient) to be optimized. For simplicity in mathematical modeling, we have used simple composites (laminated) to illustrate a general scheme for the design of phantoms for the calibration of ultrasound equipment. The general scheme consists in finding out of a given class of phantom-composites those that exhibit the best combination of the relevant parameters. Three fundamental stages stand out. First, from experimental measurements of the acoustic properties of each individual material, to obtain their mechanical properties (e.g., Formulas (1)). Second, using such mechanical properties, and applying some suitable mathematical homogenization technique, the effective properties of the composite phantoms are obtained (e.g.: Formulas (2)). Finally, using the inverse procedure to that of first stage (Formulas (1.1)), determine the effective acoustic properties and carry out the corresponding optimization process between the relevant parameters.

The effective properties of laminated composite materials can be calculated using analytical formulas (e.g., Equations (3)) that do not generate any computational cost. For example, using MATLAB, the curves in Figures 2 and 3 are generated in thousandths of a second. However, in general, calculation of effective properties of composite materials involves a high computational cost that requires the application of advanced numerical and computational techniques such as: Fast Fourier Transform (^{Moulinec & Suquet 1998}), Finite Element Method (^{Caballero-Pérez et al. 2020}), Parallel Computing (^{Eder et al. 2004}), Image Based Modeling and Deep Learning (^{Li et al. (2019)} and Artificial Neural Networks (Liu et al. (2001), among others.

Beyond the present preliminary study, through homogenization techniques and methods it is possible to account for many other geometries of the tissue analogues. For instance, one particular homogenization technique (Asymptotic Homogenization) has been used for curved laminates (^{Guinovart-Sanjuán et al., 2016}). Such non-planar geometry is relevant for studying phantoms since it decreases energy losses due to reflection. Furthermore, random shapes of the analogues can also be dealt with through numerical methods such as the FFT-based that was employed here for validation. Furthermore, homogenization methods can also account for non-linear effects that the materials for phantoms may also exhibit (^{Manickam et al., 2014}). As far as we know the methodology of applying mathematical homogenization techniques for the design of phantoms is new.

As near future work, some prototypes based on the described model will be built employing additive manufacturing techniques (Filament Fusion Fabrication). The selection of the central layer material (Agar) will be guided by the studied acoustic effective properties calculated in this work. Materials like ABS (Acrylonitrile Butadiene Styrene), PLA (Polylactic Acid) and PETG (Polyethylene Terephthalate Glycol) plastics will be tested in relation to their suitability to build the external support structure to contain the Agar. In this way, it is possible to test additive manufacturing processes that allow us to build useful composite phantoms for ultrasound applications.