Introduction
The use of forest residues for bioenergy production has gained interest in recent years because it has the potential to generate additional revenue for the forest sector and diversify energy sources (Cambero, Sowlati, Marinescu, & Dominiket, 2015). This biomass can be obtained from the management of forest plantations via pruning and thinning, or through the residues produced during harvesting (Perlack et al., 2005).
A series of studies on Pinus radiata D. Don biomass began in the 1960s in Australia, New Zealand and South Africa in order to make estimates of forest productivity and nutrient capture (Baker & Attiwill, 1985; Madgwick, Jackson, & Knight, 1977; van Laar & van Lill, 1978; Will, 1964). Subsequent studies have been conducted to understand the productivity of this species in relation to site resources, partitioning of biomass components and ecophysiological modeling (Cromer, Barr, Williams, & McNaught, 1985; Rodríguez, Hofmann, Espinosa, & Ríos, 2003; Rubilar et al., 2010). However, the use of biomass produced by forest management has certain limitations, highlighted by the inefficiency of the collection methods and the need to quantify both the biomass that would be generated from management of Pinus spp. plantations and natural forests, and the degree of contribution to bioenergy generation (Acuña, Espinosa, Cancino, Rubilar, & Muñoz, 2010; Hacker, 2005).
Recent studies in Chile have made estimates of the biomass of harvest residues in P. radiata plantations from models fitted with databases from Australia and New Zealand, using growth and yield models as a basis (Corvalán & Hernández, 2011). Similarly, conversion factors for changing stem volume to total aboveground and harvest residue biomass have been used (Bertrán & Morales, 2008).
The aim of this study was to develop models to estimate harvest residue biomass at individual tree and stand level in adult Pinus radiata D. Don plantations, in characteristic soils of south-central Chile. The developed models will allow for estimating the energy potential of P. radiata plantations in south-central Chile at site-specific level, considering management conditions and the fate of harvest residues.
Materials and methods
Selection of the study areas and sampled trees
Selection of the sampled stands was made considering the productivity and management intensity for harvest-age Pinus radiata D. Don plantations, located in soils derived from volcanic sands (Xeropsamments), recent volcanic ash (Haploxerands) and marine sediments (Hapludults) (Figure 1). The stands were selected by means of a cluster analysis definition, using a stand basal area and density records database maintained by the main forestry companies in the region over the last 20 years.
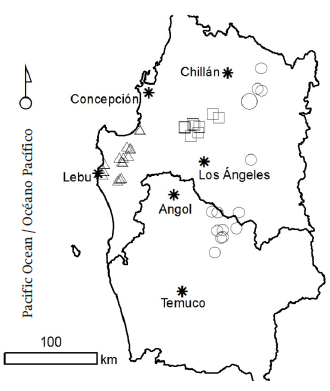
Figure 1 Geographical location and distribution of Pinus radiata D. Don stands sampled for each parent material evaluated. Squares represent stands in soils derived from volcanic sands, circles represent stands in soils derived from recent volcanic ash, and triangles represent stands in soils derived from marine sediments.
From the variables basal area (G, m2·ha-1), as an expression of stand productivity, and density per hectare (N, trees·ha-1), as a reflection of management intensity, we selected, from the harvest supply, nine stands in soils derived from volcanic sands, eight stands in soils derived from recent volcanic ash and 10 stands in soils derived from marine sediments, for a total of 27 stands, representative of a productivity gradient and management conditions in each parent material (Figure 2).
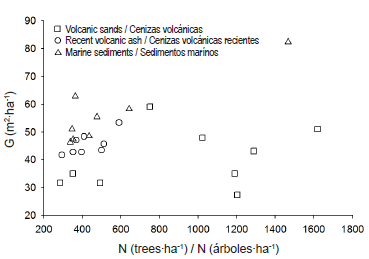
Figure 2 Productivity (stand basal area, G) and management (stand density, N) parameters of harvest-age Pinus radiata D. Don stands, selected from cluster analysis of historical productivity records of the leading forestry companies in the region, for the three soil parent materials evaluated in the study.
In each of the representative stands of the selected clusters, and considering the preharvest inventories of each stand, we selected nine to 10 sample trees, which were distributed within the diameter range of each sampled stand. The total height (H), diameter at breast height (D) and height of small end diameter (Hsed) of each selected individual were recorded. A total of 250 trees were sampled.
Biomass sampling
It was conducted from destructive methods, estimating the following aboveground biomass components: stem wood and bark, branches, living foliage, dead foliage, cones and dead crown, for each sampled tree.
Stem biomass. Wood and bark biomass was estimated from the stem cutting height (0.15 m from the base) to the apex. Cross-section samples of each tree’s stem were obtained, at every 2.5 m from the base of the stem to the small end diameter (SED = 8 cm), and at a spacing of 1 m from the SED to the apex. For each cross-section, diameters with and without bark were recorded, and basic density of wood and bark was determined. Cubing of the wood and bark volumes of each stem portion was performed. Biomass (kg·tree-1) was estimated using the weighted average basic density of each stem portion. As the weighting factor, the area of the upper and lower cross-section of each stem section was used. Merchantable stem biomass corresponded to the wood biomass between the base and the SED, while the harvest residue biomass of the stem corresponded to the wood biomass between the SED and the apex, added to the bark biomass.
Crown biomass. Crown biomass estimates were differentiated between the living crown (branches, cones, living foliage and dead foliage) and dead crown (necromass). For the living crown, the insertion diameters of all living branches along the stem of each sample tree were measured. Then five dead branches from each tree, selected to represent the distribution of branch diameters of all trees selected in each stand, were obtained. The sample branches were taken to the laboratory to determine dry weight. For this purpose they were placed in ovens at 65 °C to constant weight, dry weight was recorded to the nearest 0.1 g, and the biomasses of the branch, cone, living foliage and dead foliage components were differentiated.
For each sampled stand a regression model was fitted for the branch and living foliage components, using as the independent variable the insertion diameter of the branch. The model used to estimate the biomass of these components corresponded to a potential linearized structure model [1] with bias correction, using the correction factor proposed by Baskerville (1972) [2]. The fitted models were used to determine the biomass of each sample tree from the branch insertion diameters. For the cone and dead foliage components, the average biomass among the sampled branches of each stand was used, given the null relationship to insertion diameter. The average values were multiplied by the number of living branches of each sample tree to obtain the biomass of these components.
where:
biomass of branch i (g), in the branch (Ra) and living foliage (Fv) components |
|
b0, b1 |
regression coefficients |
insertion diameter of branch (mm) |
|
ei = |
residue |
where:
bias correction factor of the fitted model |
|
MSE = |
mean squared error of the fitted model |
Necromass was estimated by collecting all the dead branches of each sampled tree, which were weighed in the field to the nearest 20 g. Subsequently, an approximately 1,000 g sample was obtained and then weighed in the field to the nearest 0.1 g. The necromass sample was taken to the laboratory and dried in an oven at 65 °C to constant weight, and its dry weight was recorded to the nearest 0.1 g. From the dry and wet weight of each necromass sample, the total necrosis of each sampled tree was determined [3].
Estimation of the potential biomass of harvest residues
The potential biomass of each tree’s harvest residues was estimated by adding the dry weight of the non-merchantable stem wood (between SED and apex), stem bark, branch, living foliage, dead foliage, cone and necromass components.
Conversion factor for potential biomass of harvest residues
The biomass conversion factor was estimated using the ratio of potential harvest residue biomass to merchantable stem biomass, expressed as a percentage. From the observed values the fitting of a regression model proposed by Jenkins, Chojnacky, Heath, & Birdsey (2003) [4] was performed for each parent material, using diameter at breast height (1.3 m above ground level) as the independent variable.
where:
biomass conversion factor for estimating potential harvest residue biomass (%) |
|
potential harvest residue biomass of tree i (kg·tree-1) |
|
biomass of the merchantable stem portion of tree i (kg·tree-1) |
|
Exp = |
exponential function |
b0, b1 = |
regression coefficients |
Di = |
diameter at breast height of tree i (cm) |
ei = |
residue |
Fitting of estimation models for the potential harvest residue biomass
The fitting of a regression model in a potential linearized structure [5] was performed using the independent variable “D2H”, with incorporation of indicator variables (for each parent material) and subsequent use of the bias correction factor [2].
where:
potential harvest residue biomass of tree i |
|
Di = |
diameter at breast height of tree i (cm) |
Hi= |
total height of tree i |
b0, b1 = |
regression coefficients |
ei = |
residue |
Using the models fitted at individual tree level and stand tables for preharvest inventories, scaling up the potential harvest residue biomass to stand level was performed. Fitting of a regression model [6] was then performed using indicator variables for each parent material.
Results and discussion
Distribution of aboveground biomass
At individual tree level, on average for the three parent materials evaluated, 73.1 ± 6.1 % of total aboveground biomass corresponds to stem wood biomass and 19.3 ± 6.2 % to crown biomass, while the potential harvest residue biomass reaches on average 29.2 ± 7.8 % of total aboveground biomass (Table 1).
Table 1 Distribution of total aboveground biomass at individual tree level for adult Pinus radiata D. Don plantations for each soil parent material evaluated.
| Parent material | |||
|---|---|---|---|
| Biomass component | Volcanic sands | Recent volcanic ash | Marine sediments |
| Stem wood | 70.01 ± 5.99 b | 74.12 ± 5.47 a | 75.19 ± 5.60 a |
| Stem bark | 7.56 ± 2.16 a | 7.62 ± 1.80 a | 7.61 ± 1.85 a |
| Necromass | 7.19 ± 4.18 a | 4.50 ± 3.64 b | 3.99 ± 2.07 b |
| Branches | 8.09 ± 4.10 a | 7.71 ± 3.90 a | 7.08 ± 3.52 a |
| Living foliage | 3.88 ± 1.47 a | 2.66 ± 0.99 b | 2.90 ± 1.23 b |
| Dead foliage | 0.24 ± 0.46 ab | 0.33 ± 0.29 a | 0.16 ± 0.11 b |
| Cones | 3.03 ± 2.95 a | 3.05 ± 4.07 a | 3.07 ± 2.99 a |
| Potential harvest residue biomass | 34.18 ± 8.50 a | 27.3 ± 6.40 b | 26.18 ± 5.52 b |
Average values ± standard deviation are indicated. Volcanic sands n = 84; Recent volcanic ash n = 73; Marine sediments n = 93.
Results for the distribution of stem wood biomass and crown biomass (necromass + living foliage + dead foliage + cones) are similar to those obtained by Canga, Dieguez-Aranda, Afif-Khouri, and Cámara- Obregón (2013) in P. radiata plantations in Asturias, Spain, where stem wood biomass and crown biomass accounted for 72 and 18 % of total aboveground biomass respectively. Merino, Rey, Brañas, and Rodríguez-Soalleiro (2003) report that in adult P. radiata plantations in Galicia, Spain that 70 and 22 % of aboveground biomass corresponds to stem wood biomass and crown biomass, respectively. Balboa- Murias, Rodríguez-Soalleiro, Merino, and Álvarez- González (2006) report for P. radiata that 72.5 ± 5.1 % of total aboveground biomass corresponds to stem wood biomass, and 18.7 % to crown biomass. The minimal differences between the different studies and parent materials may correspond to differences in site management and productivity activities associated with the type of soil (Schalatter & Gerding, 1999).
Conversion factor for potential harvest residue biomass
Potential harvest residue biomass estimates represent on average 43.3 ± 19.3 % of merchantable stemwood biomass, considering an SED = 8 cm. The estimated conversion factor has a close relationship with tree size, which agrees with what was proposed by Jenkins et al. (2003), where for smaller-sized individuals the proportion of biomass distributed to merchantable stemwood is less than for larger-sized individuals (Table 2, Figure 3).
Table 2 Fitted models for estimating the conversion factor for changing stem biomass to potential harvest residue biomass (BCFPHR) for Pinus radiata D. Don plantations for the parent materials evaluated.
| Parent material | Fitted model | N | MSE | R2 |
|---|---|---|---|---|
| Volcanic sands | 84 | 319.2 | 091 | |
| Recent volcanic ash | 73 | 152.6 | 0.91 | |
| Marine sediments | BCFPHR=36.2 | 93 | 105.6 | --- |
n: number of observations for fitting the model. MSE: mean squared error of the fitted model. R2: coefficient of determination of the fitted model.
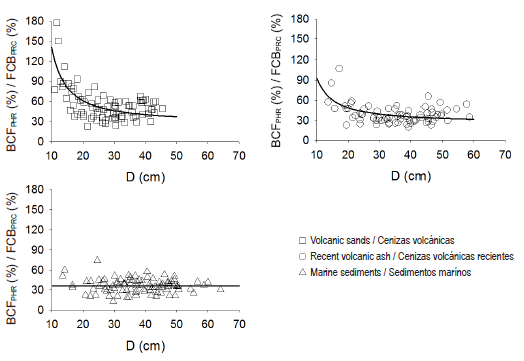
Figure 3 Relationship between the conversion factor for changing stem biomass to potential harvest residue biomass (BCFPHR, in %) at individual tree level, and diameter at breast height (D, in cm), for Pinus radiata D. Don plantations in each parent material evaluated.
Estimation of potential harvest residue biomass at individual tree level
The results of fitting models for estimating potential harvest residue biomass for each tree, performed by means of indicator variables (dummy variables), suggest a differentiated fit between parent materials of volcanic origin (volcanic sands and recent volcanic ash) and those derived from marine sediments, difference of the intercept P = 0.0254, difference of the slope P = 0.0375 (Table 3, Figure 4). This may be related to soil fertility levels and more favorable weather conditions for the development of the species in the case of soils derived from marine sediments (Schalatter & Gerding, 1999).
Table 3 Models for estimating potential harvest residue biomass for adult Pinus radiata D. Don plantations at individual tree level, for the parent materials evaluated.
| Parent material | Fitted model | n | MSE | R2 | Final model |
| VS and RVA | ln(BPHR) = -3.74850 + 0.83850 × ln(D2H) | 157 | 0.07144.0000 | 0.90.0 | BPHR = 0.02441 × (D2H)0.83850 |
| MS | ln(BPHR) = -3.74850 + 0.83850 × ln(D2H) | 93 | 0.08529.0000 | 0.86.0 | BPHR = 0.00876 × (D2H)0.92962 |
VS: Volcanic sands. RVA: Recent volcanic ash. MS: Marine sediments. n: number of observations for the model fit. MSE: mean squared error of the fitted model. R2: coefficient of determination of the fitted model.
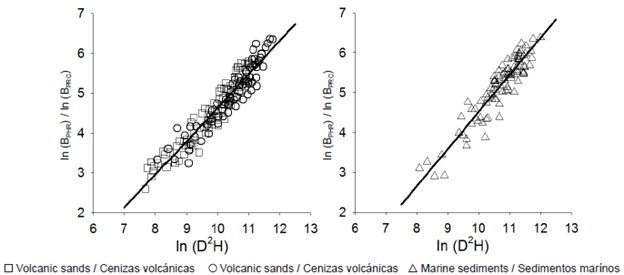
Figure 4 Relationship between potential harvest residue biomass (ln BPHR) and the independent variable (ln D2H) at individual tree level for adult Pinus radiata D. Don plantations, clustered as a result of regression analysis with indicator variables.
The structure of the fitted estimation model has been mainly used for estimating total aboveground biomass (Moore, 2010) and stem wood and bark biomass (Canga et al. 2013), not only for P. radiata but also for other species (Ter-Mikaelian & Korzukhin, 1997), and a good fit for estimating potential harvest residue biomass at individual tree level has been observed.
The fitted estimation model uses variables that can be quickly measured in the field, allowing easy applicability to make estimates at individual tree level and later scaling up to stand level. In addition, it is one of the broader-scope studies regarding biomass assessment for harvest-age P. radiata, for estimating the potential residues that would be generated after harvesting activities in plantations of this species.
Estimation of potential harvest residue biomass at stand level
Several studies have fitted biomass estimation models at individual tree level at the local and regional scale (Canga et al. 2013, Jenkins et al. 2003, Merino et al. 2003; Moore, 2010; Rodríguez et al. 2003; Rubilar et al. 2010). However, few are those that after scaling biomasses up to stand level for P. radiata fit estimation models at this scale (Bi et al. 2010; Corvalán & Hernández, 2011). On the other hand, there are those who have explored some relationships (Cromer et al., 1985; Madgwick et al. 1977; Madgwick, 1985), where they identify variables such as average stand height, basal area and stand density as predictors of biomass at stand level.
In arriving at estimates for potential harvest residue biomass at stand level, using estimation models at individual tree level together with stand tables, a close relationship with stand basal area (G), independent of parent material, was observed (Figure 5). Bi et al. (2010) report basal area as one of the variables to be incorporated into biomass estimation models, by components and total aboveground biomass.
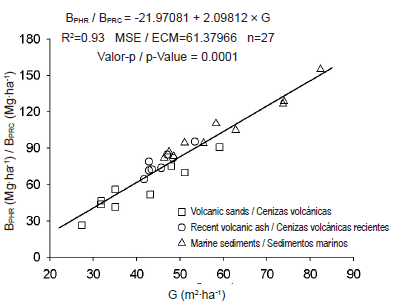
Figure 5 Fitted relationship between potential harvest residue biomass at stand level (BPHR) and stand basal area (G), for adult Pinus radiata D. Don plantations.
From the fitted relationship it would be possible to estimate potential harvest residue biomass, independent of the silvicultural management activities that are carried out in P. radiata plantations, their productivity and soil parent material.
With the proposed models at individual tree and stand level, estimates of potential harvest residue biomass can be made. However, biomass that is currently removed from harvested sites, for energy purposes, is the combinatorial result of harvesting methods, collection and potential residue biomass. Future validation, with field data, of the biomass of residues that would be exported after operational removal activities in Pinus radiata stands is necessary.
Conclusions
The fitting of an estimation model of the conversion factor for changing stem biomass to potential harvest residue biomass for P. radiata suggests a fit dependent on the parent material, where the species has a differentiated aboveground biomass distribution. However, it is independent of stand productivity and management.
The fitted models for estimating potential harvest residue biomass for P. radiata at individual tree level suggest a fit dependent on the origin of the soil parent material. In the case of the estimation model fits at stand level, there is a close relationship with stand basal area, regardless of productivity levels, management regime and parent materials evaluated.
The fitted models would be applicable in a wide range of management and productivity conditions, for P. radiata plantations in south-central Chile. However, for studies aimed at estimating potential harvest residue biomass, subsequent validation with field-collected data on the biomass of harvest residues removed during post-harvest activities is recommended. This is because the biomass that is currently removed would not only have a relationship to potential harvest residue biomass, but also to the harvesting and material collection methods, which would determine the efficiency of the harvest residue collection operations.











 texto en
texto en 








