Introduction
The development of energy generation and cogeneration devices through renewable energy resources has been increasing, due to the effects generated by using fossil fuels to generate electrical energy or heat mainly. The greatest effect of the use of non-renewable energy resources is global warming, in addition to its gradual exhaustion. Under this premise, it is considered that solar energy is the one with the greatest impact at present and generates the greatest benefit to humanity due to its minimal damage to the environment, being free in addition to its availability. For this reason, the study of new hybrid energy generation systems is of great importance, mainly based on renewable energy resources, where the most significant so far is the use of solar energy as a primary source.
The significant advantage of solar energy is that its conversion is direct, although so far it is not very efficient; For example, photovoltaic energy converts solar energy into electricity due to the photovoltaic effect, but with a yield of no more than 25%, or in its case, solar thermal energy that converts solar energy into thermal energy due to the absorption capacity and mechanisms of heat transfer developed in the system that also have a performance of up to 75%. It is also possible to have cogeneration systems that increase their overall performance, by combining photovoltaic and solar thermal, up to 85%. It is for this reason that governments together with the International Renewable Energy Agency (IRENA) have developed a vision perspective for 2050 with the purpose of achieving at least an 86% participation in electricity generation with renewable energies, (IRENA,2019). Mexico regarding the use of solar energy does not exceed 2% of participation for the production of electrical energy, unlike 79% from fossil fuels, (IRENA,2015), (SENER, 2018). Therefore, it is necessary to increase the active use of alternative energy to produce electrical energy, and thus take advantage of the country’s solar potential since it can be considered one of the most promising renewable energy sources, mainly due to its easy access.
The development of energy generation and cogeneration devices depends on the quality of solar energy and on design parameters. So, by optimizing the design parameters it is possible to increase its efficiency, durability, reliability, as well as the safety aspects and competitive costs. For this reason, this work integrates a mathematical simulation model that allows a quantitative and qualitative analysis of a thermal photovoltaic hybrid system and a sensitivity analysis of the system design parameters.
Applications of solar energy have been studied extensively, particularly those of direct conversion, such as solar thermal and photovoltaic (Ramos, G. L., 2012), (Wu Y., Wu S., and Xiao L., 2017), (Apatekar, S., & Mallareddy, Ch., 2015), (Syafiqah Z., Irwan YM., Amin N., Irwanto M., Leow WZ. and Amelia AR., 2017). Most of the studies based on photovoltaic cells have been directed towards the modeling and simulation of equivalent circuits such as the simple diode, in order to analyze the influence of solar radiation, cell temperature, and weather conditions on the behavior of the photovoltaic module in stationary or dynamic state, as is showed in, (Amelia A.R., Irwan Y.M., Leow W.Z., Irwanto M., Safwati I., Zhafarina M., 2016), (Belhadj, C., Kassas, M., & Essamuddin, S., 2015), (Desisaa D. G., Shekatab G. D., 2020).
Jangwoo, P., Hong-geun, K., Yongyun, C., & Changsun, S., (2014) studied the mathematical modeling of a photovoltaic cell using equivalent circuits that include the effects of solar radiation, operating temperature, as well as some module construction parameters. The model is developed in MatLab / Simulink using maximum power point techniques. Another important parameter in the study of photovoltaic modules is the temperature response with respect to the change in incident radiation, which is considered dynamic and cannot be analyzed in detail in a stationary model. For this reason, various stationary and dynamic models have been studied to determine said time constant, in addition to the effects that cell temperature causes on energy conversion, as well as the non-linearities of the system, as is showed in (Armstrong, S., & Hurley, W. G., 2010), (Sadeghzadeh, M., Ahmadi, M. H., Kahani, M., Sakhaeinia, H., Chaji, H., & Chen, L., 2019), (Patel G. A., 2016), (Manjunath, M. S., Karanth, K. V., & Sharma, N. Y., 2018), (Libra M., Poulek V., Kouřím P., 2017), (Yeshalem M. T. and Khan B., 2017), (Singh, A. P., & Singh, O. P., 2018).
Another case study is that of solar water heaters, which for several decades ago have been exhaustively analyzed by researchers, and currently it has been possible to have a maturity in effective knowledge about the various models, their applications and in general greater reference is made to the flat plate, mainly due to the simplicity in developing its energy analysis (Armstrong, P., 1978). Numerical analyses of the behavior of the solar collector based on heat transfer and energy balance have been performed, as is showed in, (Paz, G. J. C., 2005), (SOLARTRONIC, 2003). Taking these analyses as a basis, mathematical models of hybrid systems called photovoltaic-thermal based on water or air have been developed. These hybrid systems are considered more thermally efficient, since a photovoltaic cell loses efficiency by increasing its operating temperature, and a solar collector can become a heat sink for the cell when combined. These types of devices are called cogeneration systems, since at the same time they generate electrical and thermal energy depending on the same energy source. It also allows the energy conversion mechanism to be more efficient in both cases (Chow, T. T., Tiwari, G. N., & Menezo, C., 2012), (Preet S., Bhushan B., Mahajan T., 2017).
The configurations developed for this cogeneration system may depend on the type of working fluid, geometry, heat transfer mechanism, materials, among other constructive characteristics. In thermal photovoltaic-cogeneration systems based on water, thermal efficiency ranges of 45% to 70% have been reached, as is showed in (Jin H. J., Kadi I., Barth T., and Leszczynski E., 2017), (Stropnik R., Stritih U., 2016). This has served to understand that the effect of temperature on photovoltaic modules reaches a relative decrease in efficiency of up to 15% if the temperature increases a range of 30 K, as is enounced in, (Kasaeiana A., Khanjaria Y., Golzaria S., Mahian O., and Wongwises S., 2017), (Kazemiana A., Salarib A., Hakkaki-Fard A. and Maa T., 2019), (Khanjari Y., Pourfayaz F., and Kasaeian A.B., 2016).
In order to analyze this type of hybrid photovoltaic-thermal energy cogeneration systems, this work develops a mathematical model of a hybrid photovoltaic-thermal collector based on the mechanisms of heat transfer and energy balance in a quasi-stable state. This model allows simulating the energy behavior of the hybrid system, taking solar radiation, ambient temperature, and wind speed as a function of time as input. It also allows considering the independent modeling of a flat plate solar collector and a single diode equivalent circuit to simulate the behavior of the photovoltaic cell. The simulation model is carried out in MatLab and allows analyzing the operating characteristic curves of the cell, solar collector, and hybrid system. cooperation.
Materials and Methods
Hybrid system model
The system that was developed for this work consists of the assembly of a photovoltaic cell with an absorber plate, which allows the photovoltaic module to be cooled through the passage of a fluid flow. This work describes the mathematical model of the hybrid photovoltaic cell collector system, which allows evaluating the thermal and electrical behavior of the hybrid system. Furthermore, the same model allows the sensitivity of the system to be analyzed according to the working fluid and the geometry of the absorber plate.
The mathematical model was developed from an energy balance considering the first law of thermodynamics, as well as the correlation of heat transfer mechanisms in the steady state system. The hybrid system has as fixed input the intensity of the solar radiation with respect to the inclination plane, the ambient temperature surrounding the system, and the average wind speed of the surrounding medium. In addition to the fixed inlets, it is possible to consider as input the flow rate of the fluid passing through the collector, the geometry of the system and the positioning with respect to the horizontal. Then the main outputs of the system are the electrical power produced, and the heat absorbed by the plate through the fluid. But as output it is also possible to consider the temperature of the photovoltaic cell, the temperature of the water at the outlet of the collector.
The mathematical model of the hybrid system is described generally through an analogy of thermal resistances. The first energy balance is carried out in the photovoltaic module. Here it is considered that the incoming energy is the effective solar radiation 𝑞"s, and the outgoing energy is the effective electric power 𝑞"ele, heat lost by convection is 𝑞"conv, heat lost by radiation is 𝑞"rad and the residual heat of the photovoltaic system I 𝑞"upv; where the units of the energy balance are given in unit of power by unit area. The Figure 1. shows the Hybrid System Mathematical Model like resistances and energy flows.
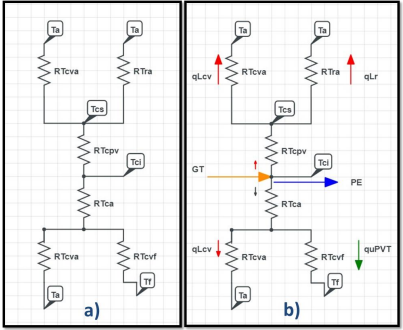
Source: Own.
Figure 1 Hybrid System Mathematical Model: a) Analog representation of hybrid system mathematical model in thermal resistances. b) Analog representation of hybrid system mathematical model in energy flows.
To adjust the model of the hybrid system, a linear model of the efficiency of the photovoltaic panel with respect to the cell temperature was developed. This model correlates the electrical efficiency of the solar module with the temperature reached by the cell under normal operating conditions in the solar plant of the solar energy laboratory of the Tecnologico Nacional de Mexico Campus Ciudad Juarez. This model is described in eq. 1 and in the same way in Figure 2.

Source: Own.
Figure 2 Linear model of the efficiency of PV Cell with respect to the cell temperature.
Then, the energy conservation model for the steady state photovoltaic cell is described in eq. 2.
where the effective solar radiation, described in eq. 3, depends of the transmittance
heat loss by convection, described in eq. 4, depends on the convective coefficient (h), ambient temperature (Ta) and cell temperature (Tc).
heat losses due to radiation, described in eq. 5, depend on the Stefan-Boltzmann constant
where the effective electrical power, described in eq. 6, depends on the transmittance
The second energy balance is performed on the absorber plate considering that a residual heat 𝑞"𝑢𝑝v is obtained from the photovoltaic panel, which is transferred to the fluid through a finned system type heat exchanger, better known as a flat plate collector. In particular, for this system it must be considered that in its development there is a heat removal factor (Fr) and a minimum amount of energy losses by convection. Therefore, this system absorbs the residual heat from the photovoltaic module and is transferred to the fluid to have a useful process heat called 𝑞"𝑢PVT as described in eq. 7.
Where (Up) is the overall heat transfer coefficient and T 1 is the inlet fluid temperature.
Finally, and in addition to this model, another equation is provided to adjust the cell temperature based on the estimation of the residual heat and the useful process possible to extract from the system and thus obtain the calculated cell temperature (Tcc) based on the proposed model, described in eq. 8.
Algorithm of simulation
The model requires an iterative process for the adjustment and estimation of the parameters dependent on the cell temperature. It also requires the vectors and input parameters. Considering that they are two independent systems, but coupled to form one, the entire system will be co-dependent on the parameters of the photovoltaic module and solar collector. Therefore, the model must be powered with the input parameters and vectors of the photovoltaic panel, solar collector and solar energy.
In the case of the photovoltaic cell, the constructive parameters of the type of solar cell are required. In addition, the algorithm considers in its iteration the simple diode model of a photovoltaic cell to estimate its parameters and behavior as a function of radiation. The parameters that are estimated are generated current (I), developed voltage (V), electrical power (P) and electrical efficiency
For the analysis of the algorithm sensitivity, it is possible to modify the constructive parameters of the hybrid system, working fluid and input vectors such as irradiation and ambient temperature. At the entrance, some of the construction parameters related to the type of cell to be evaluated (polycrystalline or monocrystalline), solar collection area, temperature of the working fluid and rate of operating flow, which are entered by the user. After, we are using the algorithm of simulation of the mathematical model of the hybrid photovoltaic-thermal collector system to estimate the process of generate energy like electrical and heat. The thermal performance analysis of the hybrid system is obtained as a function of the heat absorbed by the collector, described in 9.
Like the thermal performance estimated by the algorithm, the electrical performance of the cell, described in eq. 10, is obtained by adjusting the electrical efficiency of the photovoltaic panel itself, which is dependent on the temperature of the adjusted cell.
Finally, the overall performance
The algorithm that evaluates the performance of the hybrid photovoltaic-thermal collector system is described through the following flow diagram as shown on Figure 3.
Results
In the evaluation of the behavior of the mathematical model of the hybrid system, the steps described through the flow diagram are followed. Therefore, it is necessary to consider the two alternative algorithms which are described in Appendix A.
The first of them is the photovoltaic cell model based on a simple diode, in this case the analysis is considered through the NOCT parameters and constructive parameters of the photovoltaic cell, described in Table 1 and Table 2 respectively. Subsequently, the second model is evaluated, which is the flat plate collector, which simulates the absorption of residual heat from the photovoltaic cell, that is, the energy source ceases to be the sun and becomes the photovoltaic cell. For the analysis of this model, the construction parameters of the flat plate collector described in Table 3 are required.
Table 1 Nominal Operating Cell Temperature Parameters.
| Parameter | Value |
|---|---|
|
|
45 C° |
|
|
20 C° |
|
|
800W/m2 |
|
|
0.1 |
|
|
0.9 |
Source: Sun. V, (2020).
Table 2 Photovoltaic Cell Parameters Model SAYA-P130-28.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Pmp | 129.42 W | Gref | 1000 W/m2 |
| Imp | 8.254 A | Tc,ref | 298K |
| Vmp | 15.68 V | AM | 1.5 |
| I sc | 9.12 A |
|
0.00053 A/K |
| Voc | 18.23 V | k | 1.381𝑒 −23 𝐽/K |
| Nc | 28 | q | 1.602𝑒 −19 C |
| A | 1.3 | egev | 1.12 𝑒V |
Source: SAYA-P130-28, https://www.panelsolarmx.com/contenido/productos.html.
Table 3 Flat-Plate Collector Parameters.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| KT |
|
nT |
|
Source: Own.
Finally, to start the evaluation of the hybrid system model, representative input parameters are required, such as: solar radiation, ambient temperature, cell temperature, wind speed, fluid temperature, solar geometry, simulation time and flow. Table 4 describes in detail the values to be entered.
Table 4 Representative Input Parameters.
| Parameter | Value |
|---|---|
|
|
|
|
|
|
|
|
0.9 |
|
|
6 hrs |
|
|
12 hrs |
|
|
0.25 |
|
|
|
|
|
|
|
|
|
|
|
|
Source: Own.
Considering the parameters described from Table 1 to Table 4, it was possible to simulate the behavior of the system taking into account as variables of the algorithm: the magnitude of the flow that is passed through the collector, as well as the temperature at which fluid enters the system. Therefore, these two parameters are considered as the control variables of the system, since they can be controlled during the evolution of the system, with the purpose of maximizing the operating conditions regarding the extraction of heat from the photovoltaic cell.
Discussion
Then, to evaluate the simulation algorithm, a combination is performed with the control variables as shown in Table 5. The first simulation keeps the parameters of fluid temperature at the inlet and flow magnitude fixed and can be considered as the reference point Because they are the same values described in Table 4.
Table 5 Combination of Control Variables.
| Parameter Value | Value | Simulation |
|---|---|---|
|
|
19 °C | 1 |
|
|
|
1 |
|
|
9 °C | 2 |
|
|
|
2 |
|
|
19 °C | 3 |
|
|
|
3 |
|
|
9 °C | 4 |
|
|
|
4 |
Source: Own.
In the case of the second simulation, the flow rate of the water entering the system remains fixed and the temperature of the fluid is reduced by half. In the third simulation, the temperature of the fluid at the inlet remains fixed and the flow rate is doubled. Finally, in the fourth simulation, the temperature of the fluid at the inlet is halved, and the flow rate is doubled. These combinations allow us to evaluate the behavior of the system, as well as the simulation algorithm under its sensitivity conditions.
Figure 4 allows to observe the representative parameters of input to the system for the simulation algorithm such as: input solar radiation, ambient temperature, cell temperature and cell efficiency. It should be noted that these parameters are simulated and are obtained from the equations described in Table 4.
Figure 5 shows the results obtained from the simulation when evaluating the photovoltaic cell model and the photovoltaic thermal hybrid system, considering the first simulation case described in Table 5. These graphs show the behavior of the residual heat generated in the photovoltaic cell, as well as the increase in cell temperature. In addition, the possible heat residual to be extracted by the hybrid system, the efficiency and the power reached by the system are observed.
Figure 6 shows the comparison between the simulation results of the photovoltaic cell and the hybrid system. Here a comparison is shown between the residual heat generated by the photovoltaic cell (blue curve) and the amount of residual heat extracted by the hybrid system (red curve). Another of the graphs shown in figure 5 is where the effect of the photovoltaic cell temperature (blue curve) and the temperature of the photovoltaic cell achieved considering the hybrid system (red curve) is compared. The effect is also presented in the comparison of the efficiency of the system.
Figure 7 shows the results obtained in the photovoltaic cell integrated in the hybrid system, here you can see the characteristic curves of the photovoltaic cell;
For the case of the second simulation where the temperature at which the fluid enters the system is modified, the results are presented through Figure 8-10. Where figure 8 shows the influence that the modification of the control variable has, mainly on the temperature reached by the photovoltaic cell.
The results of the third simulation are presented through Figure 11-13, where the modification that the simulation presents depends on the change in the inlet flow in the system. Where figure 11 shows the influence that the modification of the control variable has, mainly on the temperature reached by the photovoltaic cell.
Finally, the results of the fourth simulation are presented through Figure 14-16, where the change presented by the simulation depends on the modification in the flow rate and temperature of the fluid entering the system. Where in figure 15 the influence of the modification of the control variables is observed, mainly in the temperature reached by the photovoltaic cell.
Conclusions
Mathematical modeling of hybrid energy systems today allows an exhaustive analysis of the behavior and capacity of hybrid systems for the transformation and generation of energy using renewable energies as a primary source. Likewise, these types of models allow estimating and modeling energy generation at a future time, considering the technical and economic feasibility of these systems.
This type of modeling of hybrid energy systems can become quite a useful tool for the designer of energy systems, potentially for large-scale power generation. Due to its adaptability as it allows adjusting algorithm parameters to quantify the amount of energy produced in the life cycle of the system, as well as adjusting the control variables to optimize the design of these systems on a large scale.
In conclusion, the model presented in this work allows analyzing and quantifying the behavior of a hybrid photovoltaic-thermal system and modeling various scenarios that allow us to optimize the design of this type of system to increase its overall efficiency by adjusting its control variables. Furthermore, it is possible to estimate various operating conditions using different solar radiation models that allow analyzing the behavior of hybrid generation systems under quasi-stable operating conditions.
In addition, as future work, we are working with the design of simulation models and evaluation of the performance of photovoltaic systems and photovoltaic hybrid systems through the use of techniques based on the internet of things and applicability to industry 4.0, in the solar plant. from the Institute of Ciudad Juarez.
Future Research Line
As mentioned, and according to the results, the replication of this type of project in various simulation environments and pilot plants for data collection in various regions will allow the model's capabilities to be expanded. Therefore, future work is focused on the design and development of a power generation plant from solar and hydrogen. The research objective is to work with the modeling of dynamic and chaotic systems.











 nueva página del texto (beta)
nueva página del texto (beta)

















