1. Introduction
The wide technological applications of phosphate glasses enable it to be considered of much relevance in science of glass such as laser protections and nuclear applications [1-11]. The easiness of network modification of the zinc phosphate glasses through additive strong glass forming character, low glass transition temperature, and high thermal expansion coefficient make them of significant interest in glass research [12,13]. These characteristics allow phosphate glasses to be used in many applications like manufacturing glass-polymer, laser host materials, and solid electrolytes in solid-state ionic devices. However, the former phosphate glasses can be doped with the transition metal oxides (TMO) which act as a modifier. One of the favorable transition metal oxides is nickel oxide, which makes changes in the chemical composition of glass. If merged with the vitreous network of the glass, this combination leads to the gerenation of a homogeneous local ligand field Also, the nickel ions in 3d8 electronic configuration are extremely stable in a glass network, even at room temperature [14-17]. Therefore, this work is devoted to the presentation of the structural modifications and the site symmetry around Ni2+ ions, which can be well observed in the electron spin resonance (ESR) and VSM results. Moreover, the spin-Hamiltonian, number of spin (N), magnetic susceptibility (χ), bonding coefficients, and magnetic parameters show a continous nonlinear change. This may be due to change in ligand filed around Ni2+, ions which exist due to the host material.
2. Experimental procedures
The starting materials used were NaCO3, ZnO, (NH4)H2PO4, and NiO. The glassy samples with composition 42P2O5-40ZnO-(18-x)Na2O-xNiO, where x = 1, 2, 3, 4, 5, and 6 mol. %, were prepared using the melt quenching technique. Then, the mixtures of chemicals were well-grounded after carefully measuring the calculated ratios. Then, they were melted in an oven at 1000◦C for 1 hour. Finally, the melted samples were quickly quenched by infusing them on a stainless-steel plate and covered with another stainless-steel plate. This casting happened in a muffle furnace, which annealed at 250◦C for 2 hours, after which the furnace was turned off and the glass samples were allowed to cool inside of the furnace for 24 hours.
XRD patterns of the resulting products were carried out using a Brucker D8-advance X-ray powder diffractometer with Cu Kα radiation (λ = 1.5406 Å) operating at 40 KV and 40 mA. The diffraction data were recorded between 10◦ and 80◦ at a scanning rate of 2◦/min or 0.04◦ per 0.4 s. ESR signals of nickel doped glasses rerecorded at room temperature using X-band EMX spectrometer (Bruker, Germany) with standard rectangular cavity of ER 4102 having modulation frequency 100 KHz. The magnetic properties of the produced samples powders were characterized by using a vibrating sample magnetometer (7400-1 VSM, U.S., Lake Shore Co., Ltd., USA) at room temperature in a maximum applied field of 20 KOe. From the obtained hysteresis loops, the saturation magnetization (M s ), remanence magnetization (M r ), and coercivity field (H c ) were determined.
3. Results and discussion
The XRD pattern for the prepared glass system 42P2O540ZnO-(18-x)Na2O-(x)NiO glasses doped with xNiO where 1 ≤ x ≤ 6 mol.% does not show any diffraction peak except for a halo around 20 to 40 with no indication of any peaks for crystals because of their amorphous nature shown in Fig. 1.
FIGURE 1 XRD pattern for the prepared glass system 42P2O540ZnO-(18-x)Na2O-xNiO glasses doped with xNiO where 1 ≤ x≤6 mol.%.
The two types of environments around Ni2+ ions seem to exist in both tetrahedral sites and in octahedral sites in the present glass networks. In general, tetragonally positioned Ni2+ ions do not induce the formation of any non-bridging oxygen ions but octahedrally positioned ions may act as modifiers similar to any other transition metal ions that occupy octahedral positions in the glass network. Figure 2 represents the optical absorption spectra of the studied NiO containing Na2O-ZnO-P2O5 glasses. The optical absorption spectrum of the NiO at 3 mol.% samples containing NiO has four clear bands, one with high intensity located around 438 nm and three low intense bands around 682, 814, and 1360 nm.
The three bands around 438, 814, and 1360 are categorized as octahedral (Oh) bands while around 682 is a tetrahedral (Td) band. The NiO at 1 mol.% sample has the same three octahedral bands and does not exhibit any tetrahedral band. The (Oh) band at 438 nm is associated to the spin allowed transition 3 A 2g (F) →1 T 1g (P), while the band at 803 nm can be attributed to the existence of Ni2+ ion (3d8 configuration) of the spin allowed transition 3 A 2g (3F) → 3 T 1g (F), and the band at 1360 nm is assigned to the spin allowed transition 3 A 2g (3F) → 3 T 2g (F) [13,14]. The (Td) band at 682 nm can be attributed to transition 3 T 1(F) → 3 T 1(P) [15]. The intensity of the bands is increased with the rising of NiO content.
ESR technique is used to provide information of the electronic structure of the studied samples. The ESR of transition metal ions in glasses is very interesting, because the valance state of TM changes with the variation of glass composition and the melting temperature. In the present study, the ESR spectra of phosphate glasses containing nickel oxide are measured at room temperature in order to examine the valance state of nickel in glass network. The EPR spectra of all prepared samples are characterized by very broad lines extending from 200 G to 6200 G at room temperature as shown in Fig. 3. The consequence of the crystal field a split occurs for the degenerated free ion 3 F ground state of Ni2+ ions, and the orbital singlet 3 A 2g has the lowest energy level in the octahedral structure. This is manifested in the appearance of only one symmetric resonance signal centered at (g) ≈ 2.11.
The EPR spectra are analyzed by using spin-Hamiltonian without hyperfine interaction of the form [18],
where S is the electron spin operator and is taken to be equal to 1, H is the external magnetic field, β is the Bohn magneton and g is the isotropic factor. The solution of spin-Hamiltonian gives the values of parallel (g || ) and perpendicular (g ⊥) components of ‘g’ tensor, which are shown in Fig. 4 and also are presented in Table I. The estimated values of g || and g ⊥ are continuously varying with respect to the NiO concentration. The variation of the values indicates the change in local field around the Ni2+ ions.
TABLE I The variation of components of g tensor components, bonding coefficient of Ni2+ ion were participating in resonance (N) and paramagnetic susceptibility (χ) at room temperature as a function of NiO concentration.
| NiO mol.% | g|| | g⊥ | ∆Exz,yz ×102 (m−1) | ∆Exy ×102 (m−1) | Spin number (n)×1017 (ions/cm3) |
χ×10−8 (m3/Kg) |
| 1 | 2.06021 | 2.14285 | 7409.40 | 46898.83 | 2.57 | 2.99 |
| 2 | 2.05976 | 2.14238 | 7411.19 | 47270.65 | 2.21 | 2.56 |
| 3 | 2.06066 | 2.14331 | 7408.50 | 46532.81 | 2.82 | 3.28 |
| 4 | 2.0602 | 2.14283 | 7410.29 | 46907.03 | 2.29 | 2.66 |
| 5 | 2.06044 | 2.14309 | 7408.50 | 46711.04 | 3.72 | 4.33 |
| 6 | 2.06073 | 2.14339 | 7407.60 | 46476.39 | 2.6 | 3.02 |
According to the ligand field theory, the isotropic g factor of the Ni2+ octahedral structure is shifted from the free electron value g e = 2.0023 as a consequence of the spin-orbit coupling. It is given by the relation [19]:
where λ is the effective spin-orbit coupling constant and ∆ is the energy of the transition 3 A 2g (F) → 3 T 2g (F). Using a value of 7303 cm−1 for ∆ (attained from optical results) [20] and a value of 2.11 for g, the calculated value of λ is −103 cm−1, which is 30% that of the free ion value λ = −335 cm−1 this indicates amount of covalency [21]. By using the ESR and optical spectral data, we can evaluate Owen’s ionic parameter (α 2) from the given formula:
The value of α 2 shows the type of bonding between the Ni2+ ions and the ligands. A pure covalent bond and pure ionic bond corresponding to values of α 2 that lie between 0.5 and 1.0, respectively. In our case, the calculated α 2 for all samples took the same value of 0.307 indicating a covalent nature. The obtained values of g || and g ⊥ allow the estimating of some d−d transition of Ni2+. The following equations have been used to estimate such transition [22]:
where ∆E xy and ∆E xz,yz are the heights of d xy and d xz,yz molecular orbital levels above ground state d x 2 − d y 2 respectively. The corresponding value of ∆E xy and ∆E xz,yz equals [23]
where k 2 is the orbital reduction factor and equal 0.914 [24]. The obtained values of ∆E xy and ∆E xz,yz were listed in Table I.
The ESR data can be used to calculate the paramagnetic susceptibility (χ) of the sample using the formula [25,26].
where N is the number of spins per cm3, g = (g || +2g ⊥)/3 taken from ESR data, J is the total angular momentum, K B is the Boltzmann constant and T is the absolute temperature. By using the above equation, the paramagnetic susceptibility χ is calculated at various concentrations. The paramagnetic susceptibility χ of Ni2+ ions glass system as a function of concentrations was listed in Table I.
The variation of ESR parameters with the concentration of NiO was demonstrated in Table I. By analyzing these results, it was found that the manifestation of the variation in the ligand field around Ni2+ ions was reflected in the nonlinear behavior for all ESR parameters with the concentration of NiO. In the framework of the ligand field theory, the lowest multiple terms 3F of the free Ni2+ ions splits into different levels and this splitting depends on the host material. However, in this study the main contribution comes from the changes of electron spin.
From that, the dependence of the exchange positions of integrals Ni2+ ions in the glass lattice on the interatomic distances is exponential, which seen in the optical absorption spectra at x = 1 mol.% of Ni2+ ions as first concentration, has the same three octahedral (Oh) bands [438 nm, 803 nm, and 1360 nm with spin allowed transitions 3 A 2g (F) → 1 T 1g (P), 3 A 2g (3F) → 3T 1g (F), and 3 A 2g (3F) → 3 T 2g (F), respectively] without any tetrahedral (Td) band; then, the tetrahedral (Td) band [682 nm with transition 3 T 1(F) → 3 T 1(P)] appeared with high concentration of Ni2+ ions. Meanwhile, the exchange interaction in a pair of ions in a magnetically dilute crystal is identical, other conditions being constant, with the exchange interaction in magnetically concentrated systems which this result is valid for, i.e., a weak exchange interaction when the exchange is via a paragmagnetic ion.
The magnetization of the formed NiO doped 42P2O540ZnO-(18−x)Na2O-xNiO glasses system where 1 ≥ x ≥ 6 mol.% was measured at room temperature under an applied field of 20 KOe and determining magnetic anisotropies from hysteresis loops. Plots of magnetization (M) as a function of the magnetic field (H) for different NiO ratios are shown in Fig. 5. The magnetic parameters of the produced glass system are extracted in Table II.
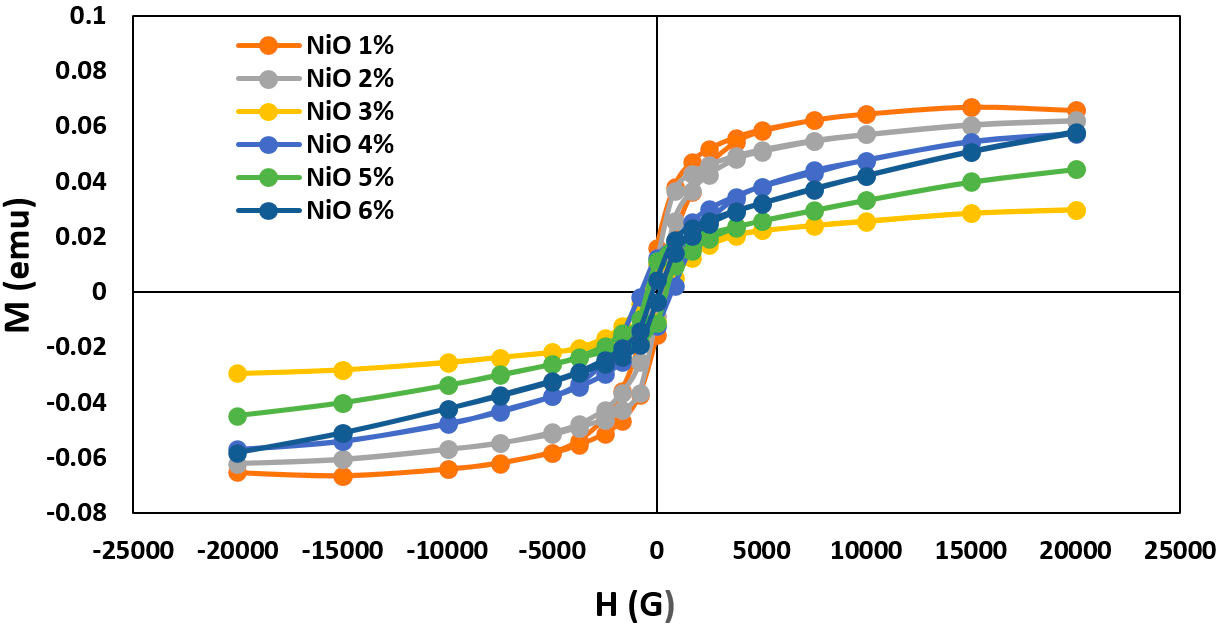
FIGURE 5 The magnetic hysteresis loops (M −H curves) of the produced 42P2O5-40ZnO-(18−x)Na2O-xNiO glasses system substituted with different NiO content from 1% to 6%.
TABLE II Magnetic properties of 42P2O5-40ZnO-(18 − x)Na2O−xNiO glasses system with different Ni2+ ions content from 1% to 6%.
| NiO mol.% | Hc (G) | Ms ×10−8 | Mr ×10−2 (emu/g) |
| 1 | 384.55 | 6.68 | 1.58 |
| 2 | 224.06 | 6.20 | 9.43 |
| 3 | 578.33 | 2.97 | 1.07 |
| 4 | 727.09 | 5.71 | 1.24 |
| 5 | 455.45 | 4.46 | 1.14 |
| 6 | 185.51 | 5.80 | 4.02 |
Figure 5 shows the paramagnetic behavior of glass matrix which clearly displays the anomalous hysteresis loop. Anomalous behavior which is initially positive before going through zero and becoming negative as shown in the inset of Fig. 5. This hysteresis behavior can be explained by modifying the amorphous disorder interface regions and also due to the coupling effect of Ni2+ ions dependent. The change in glass network by adding the NiO which arranged in both tetrahedral (Td) band and octahedral (Oh) bands symmetry sites -as discussed in optical absorbance spectra- and the number of the surrounding magnetic atoms play the rule for the continuous variation in magnetic parameters. These findings are in agreement with the ESR results.
4. Conclusion
The 42P2O5-40ZnO-(18-x)Na2O-(x)NiO, where x = 1, 2, 3, 4, 5, and 6 mol.%, glass samples are prepared by using the melt quenching method. From ESR measurements it is clear that Ni2+ ions are existing in octahedral sites with molecular orbital levels above ground state dx 2 − dy 2. The spin-Hamiltonian parameters are influenced by the composition of glass, which attributed to the change of ligand field strength around Ni2+ ions concentrations. The values of the bonding parameters are also evaluated from ESR data and it was found that the Ni2+ ions and the ligands exhibited a covalent nature. The magnetic behavior demonstrated a hysterisis curve which indicates that the NiO doped glass samples are paramagnetic materials that may be useful for developing new magneto-optical devices.











 nueva página del texto (beta)
nueva página del texto (beta)





