1.Introduction
The nitrogen-vacancy (NV) center is one of numerous point defects in diamond. It exhibits two electronic configurations: the neutral charged-state (NVo) and the negatively charged-state (NV-). The phenomenon called photochromism consists in the NV center interchange between two different charged-states by a possible mechanism involving nitrogen donors 1. Electron spins at NV centers can be manipulated by applying a magnetic field, electric field, electromagnetic radiation (light), or a combination of them, resulting in a photoluminescent signal.
The photophysics of color NV centers in diamond have attracted interest during the last decade because of their possible application in quantum information processing, quantum optics, quantum metrology, nanotechnology, as biological and sub-diffraction limit imaging, to test of entanglement in quantum mechanics and nano-medicine (sensors) 2-5. Currently, the technology tends to miniaturization, but it faces a problem: the integration techniques of circuits are not effective due to the quantum effects which become important in low dimensionality. Therefore, computational science has begun to research in quantum mechanics a new technological alternative with the aim to overcome the transistor technology.
The most promising systems are ions or atoms traps, which use their electronics states as representation of the quantum bit (qubit) states (e.g. ground and excited electronics states) 6; quantum dots in which its confined electron spins are controlled by tunneling effect via electric field and each different electron-spin configuration is used as qubit state 7,8; setting diverse magnetics polarizations as qubit states by using NMR to manipulate nuclear spins of one or lots of molecules, generally in liquid state 9,10; superconducting loops with persistent current form a qubit by superposition of two macroscopic quantum states 11; and the defects present in diamond, more precisely NV centers of which their electronic spins system are taken advantage, allowing to be initialized, manipulated, and measured (readout) by optical means 12.
At this moment, the available computing power is not enough. For this reason the Quantum Informatics become important. Apparently, the best candidate for solid-state qubit is the NV- center in diamond since it works at room temperature, has long spin coherence time as well as the diamond lattice helps as an insulator for external magnetic effects because it is diamagnetic; in addition, thanks to its high Debye temperature, the vibrational modes of the lattice are not affecting the center because there is a low coupling between lattice phonons and center electrons 13,14. In this paper a general study of internal state NV center in diamond is presented. From the second quantization formalism, -in steady-state (conservative model)- the creation and annihilation operators are used to describe the steady spin-levels structure and in dynamic-state (non-conservative model); these operators can also be used to describe different spin-level transitions. Finally, a discussion is presented about the applications of this study on different areas, especially in the photochromism phenomenon and solid-state qubit.
2.NV centers in diamond
The atomic configuration of NV center consists of two places that should be occupied with two carbon atoms but, instead, one carbon atom was replaced by a nitrogen atom and the other place is empty. In other words, there is a vacancy. The NV defect has point group C3v, where the principal axis C3 is along nitrogen-vacancy in crystallographic 11 direction; and trigonal symmetry with point group 13.
For the creation of diamond NV centers, it is necessary to create vacancies inside diamond lattice by two methods: the first one is radiating with ions, electrons or neutrons to nitrogen-rich diamond (14N) type Ib; the second one is through the implantation of nitrogen (both 14N and 15N) inside a pure diamond type IIa which creates simultaneously vacancies in the crystal lattice. Upon creation of the vacancies, it is necessary to perform an annealing process of temperatures around 550oC to 850oC (oxygen atmosphere free) producing the vacancies migration. After this process the NV centers are created 15-17.
3.Charged-states of NV center
Atomic structure of NV center in diamond consist of a carbon vacancy and an impurity of nitrogen which captures this vacancy in order to create the center, furthermore, exhibit two electronic configurations: the neutral charged-state (NVo) and negatively charged-state (NV-) 1,13,18.
In the NVo center, the nitrogen impurity has five valence electrons (being in group V of the periodic table). Three of them are shared with the three closer atoms of carbon and the other two are located in the direction of the vacancy. Thus, in the periphery of the vacancy, there exist three unsatisfied bonds, one for each of the surrounding carbons (see Fig. 1).
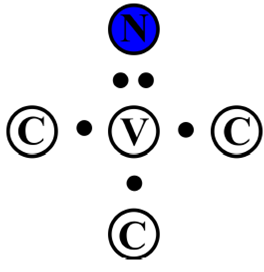
Figure 1 Schematic representation in two dimensions of the atomic configuration inside the NV0 center (where the marked circles with a C simulate the crystalline lattice), in which it can be observed that a carbon atom has been substituted for a nitrogen atom (in color blue), which captures a vacancy (marked as V) that remains with five electrons (black dots) on its direction.
The atomic configuration of NV- center is the same as the NVo center but with the only difference that it has six electrons (see Fig. 2).
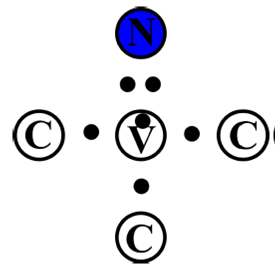
Figure 2 Schematic representation in two dimensions of the atomic configuration inside the NV - center (where the marked circles with a C simulate the crystalline lattice), in which it can be observed that a carbon atom has been substituted for a nitrogen atom (in color blue) which captures a vacancy (marked as V) that remains with five electrons (black dots) on its direction and a sixth electron positioned at the center of the vacancy.
4.Electronic configurations
4.1.NVo center configuration
As shown in Fig. 1, the nitrogen directs its full orbital towards the vacancy as well as the three surrounding carbons their semi-full orbitals point towards it. Therefore, the total spin state (S) can be only 3/2 or 1/2 since the S = 5/2 state is not possible because it would be necessary for nitrogen electrons -which point towards the vacancy- to not be paired (see Fig. 3).
4.2.NV- center configuration
As shown in Fig. 2, the nitrogen directs its full orbital toward the vacancy, the unsatisfied bonds of the surrounding carbons are oriented towards the vacancy, and probably the sixth electron is pushed towards some of the surrounding carbons by effect of the two electrons of the full orbital of the nitrogen; which would very likely result in the paring of the sixth electron with some of the carbons with unsatisfied bonds. Thus, the system could have S = 2, S = 1 or S = 0 states (see Fig. 4).
5.Spin configurations
5.1.NVo center
In the case of S = 1/2, there are two doublets: one of them being the groud-state
with
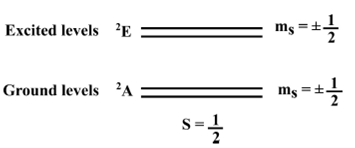
Figure 5 Schematic representation of the spin-level structure of a NV0 center in which the possible S = 1/2 spin configuration is observed.
For the case of the S = 3/2 state, there are two multiplets: one excited and the
other is the ground-state. These are made up of two doublets with
5.2.NV- center
In the case of S = 2, there are two multiplets: one excited and the other is the
ground-state. These are made up of two doublets (
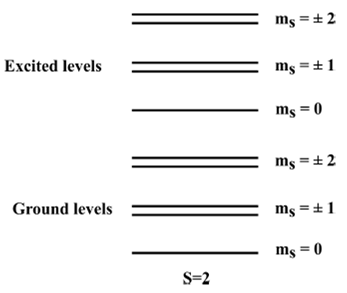
Figure 7 Schematic representation of the spin-level structure of a NV - center, in which the possible S = 2 spin configuration is observed.
Similarly, in the case of S = 1, there are two triplets: one excited and the
other the ground-state. These are made up of a doublet with
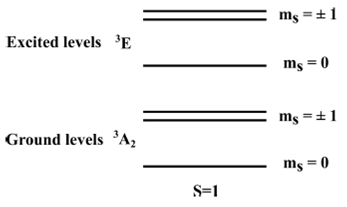
Figure 8 Schematic representation of the spin-level structure of a NV - center in which the possible S = 1 spin configuration is observed.
6.Experimental characterization
Experimentally, the NV centers in diamond are characterized by Electron Paramagnetic Resonance (EPR) or Optically Detected Magnetic Resonance (ODMR) techniques and the fluorescence signal emitted when an excited state is relaxed to a base state.
In the NV0 center, it has been detected a Zero Phonon Line (ZPL) at 2.156
eV (575 nm), which it is associated with a radiative transition (
In the NV- center, there exists a radiative transition with spin
conservation due to the selection rules present in the system (
The NV0 and NV- centers are promising candidates for
solid-state qubits because both centers have characteristics that make them
utilizable. In the case of NV0, it is possible by using a
4A2 excited level since it presents two doublets which can
be used as qubit states. Other promising choice would be to use the transition
between the ground
7.Theoretical characterization
The spin-orbital interaction, spin-spin interaction with electric and strain fields (see Eqs. (6), (8), (13), and (17)) are all Hamiltonians in terms of the Irreducible Representations (IRs) by, using Group Theory and are discussed in Ref. 30.
The electronic Hamiltonian of the NV- center (Eq. (1)) -corresponding to the ground electronic state- with an adiabatic approximation and considering the nuclei of the crystal to be fixed at their equilibrium coordinates is shown in 31. The interaction Hamiltonians of the center with electric (Stark shift), magnetic (Zeeman effect), and strain fields of Eq. (16) are shown in Ref. 32.
In Ref. 5 the ground state fine and hyperfine structures for both nitrogen isotopes can be described by the canonical spin-Hamiltonian of trigonal defects given by Eq. (1) and the potential of Eq. (2) describes the influence of static electric, magnetic, and strain fields on the NV- ground state. Also, it is shown the effective Hamiltonian and potential that describes the influence of static electric, magnetic, and strain fields for excited state 3E to low-temperature and room-temperature (see Eqs. (3)-(6)).
7.1Steady-state (Conservative model)
In the present paper, the Hamiltonian of NV center,
where the index i, and j represent the NV center electrons, μ0
represents the magnetic constant (vacuum permeability), ye and
γn are the electron and nuclear gyromagnetic constants,
respectively, S indicates the magnitude of the total electron-spin of the system
On the other hand, the steady-state solution (conservative) will be,
using the second quantization formalism, the form of a NVo center wave can be written as follows
where the index i indicates the center electrons, (r, σ, t) represent the spatial
coordinates, electron-spin and time, respectively. A symbolizes a normalization
constant, Ci is a proportional constant, and
Similarly, it is obtained the non-interacting wave function of the NV- center,
where summation is done over all different possible p permutations and
Np represents the permutation index, C1,
C2, C3 represent the three unbonded carbons, and V
represents an electron in the vacancy (see Fig.
2). Notice that the subindex on V in the function
Now, if the wave functions of NVo and NV- centers are
projected on the symmetrical occupation-number basis
and defining
When the operators given by Eqs. (11) and (12) are applied onto the wave functions of Eqs. (9) and (10), the result is
Thus, from (13) and (14), it can be concluded that
Since the previous wave functions, (7) and (8), depend on the spin σ, then they
can be rewritten as the product of their orbital wave function
Therefore, the form of the spinorial functions of the NVo and NV- centers can be obtained from
where summation is performed over all different possible permutations p of the system, C1, C2, C3 represent the three unbonded carbons, and V represents an electron to place in the vacancy (see Fig. 2). As the negatively charged-state center NV- is the best candidate to implement as a solid-state qubit based on the DiVenzo Criteria 33, it will be the focus of the present study. The electrons of NV- center that are involved in the processes of the radiative and non-radiative transitions are the three of the carbons that have unsatisfied bonds and an extra that is transferred by some close donor impurity into the vacancy. Therefore, there are four electrons participating in the different S = 0 and S = 1spin states; S = 2 will be omitted because there is not experimental evidence for this spin configuration. Accordingly, the possible forms of the spinorial function of Eq. (18) for the two different spin states in ground state are
•
•
•
•
where C1, C2, C3 represent the three unbonded carbons, and V represents an electron to place in the vacancy (see Fig. 2). Furthermore, the αk, βk, and γk states are characterized by the index k, which can take the values of C1, C2, C3, or V and are defined as
Well, if the
where
where the eight
•
•
The expressions of Eqs. (26) and (27) have been depicted in the Figs. 8 and 9 of Sec. 5.2 according to their spin-level structure.
7.2.Dynamic-state (Non-conservative model)
The dynamic Hamiltonian
where
Therefore, the dynamic-state solution (conservative) will be,
Well, substituting (10) into (30), it is possible to obtain an expression for the NV- center, namely, center
The creation and annihilation operators for the NV- center between its electron-spin states, from (31), acquire the form
where the
Fermi´s Golden Rule
where
where i is the set of spin states for each different charged-state of NV centers. If the same energy interval is chosen, therefore the number of states of a NVo center is greater than for NV-, meaning that
NVo center has two different total spin states, and these are S = 1/2 and s = 3/2.
NV- center has two different total spin states, and these are S = 1 and S = 0.
Based on the above and reviewing the spin-level structures for the charged-state of each center (see Fig. 5-6 for NVo and Fig. 8-9 for NV- ), it is concluded that the density of states of NVo p(E) is greater than the one for NV-, p´(E). The density of states on the photochromism phenomenon changes from p(E) to p´(E) and viceversa. From this fact, a total density of states pT(E) can be defined as
which, when α = 0 and b = 1, represents the density of states of NV-. In turn, if α = 1 and b = 0, it represents the density of states of NVo. Accordingly,
Therefore,
8.Discussion of results
On the previous section, the different models, assumptions, and approximations reported in the literature for NV centers in diamond. By comparison with the present model, the main differences with respect of the models above are the use of the second quantization formalism and the photochromism phenomenon.
In this section, the most important results obtained for the characterization of the NV center
internal state will be shown using the second quantization formalism, including the
photochromism effect. First, the schematic representations of the two different NV
center electronic configurations, neutral and negative charged-states, was designed
in order to clarify how the different possible configurations of each electron-spin
modify the system total spin S. The fact that diamond is the host
lattice of the NV defect plays a very important role because if it was not for the
diamond energy potential, the NV center would not exist. It must also be noted that
the defect behaves as an internal system within the diamond matrix, since the
spin-levels are in the middle, above the valence band which is populated and below
the conduction band which is empty, both bands belong to the diamond; in other
words, the electrons of the diamond lattice do not play a role within the dynamics
of the NV center. Considering the previous assertions, the Hamiltonian modeling of
the system internal state,
On the other hand, the NV center exhibits a switching charged-state process called photochromism 1. There are two different ways to describe this phenomenon:
The one described in Ref. 1 presents the hypothesis that the switch from NVo to NV- state is photoinduced. This process would be possible due to the ionization of nitrogen donors present in the surroundings of NV defect.
The other hypothesis suggested is by means of the existence of a weak interaction between NVo and NV- centers, which are created in almost the same proportion in diamond during the production process. This interaction is due to the interchange of vacancy-electron from NV- to NVo, resulting in a switching charged-state steady-process. Therefore, the creation and annihilation operators of Eqs. (11) and (12), respectively, are useful to describe the photochromism since they switch the defect from NVo to NV- center and vice versa.
Finally, from
where α and β are complex coefficients that satisfy
To make use of the NV- center as a qubit, it will be necessary to use the spin-levels of its different states, ground and excited. For example, by taking advantage of the photoluminescent response that the system undergoes, when it passes from an excited level to a ground level, the system configuration can be found, meaning that the system is read-out. On the other hand, applying a magnetic field tuned to a suitable resonance frequency, the manipulation of the electron population of ground and excited states can be achieved. Finally, due to the existence of the two different spin configuration, S = 1 and S = 0, it is possible to initialize the system in a specific spin-level.
Now that the procedure has already been proposed, it is necessary to know what spin-levels are more convenient to represent the two qubit states. There are two possibilities to represent these qubit states. The first one would be to use the ground-state levels, ms = 0 and ms = -1 -the most advisable for energy efficiency- which would represent the qubit states. To avoid the mixing between the spin levels, a magnetic field would need to be applied to make use of the Zeeman effect, splitting the levels and, consequently, decreasing the mixing probability. The other possibility is to use the photochromism phenomenon by manipulating the configuration of two different NV centers, one with S = 1 and the other one with S = 0 as qubit states. In this case, the initialization can be represented by means of one of the two configurations of total spin S; the manipulation would be through electron population distribution in different configurations of spin using magnetic and electromagnetic fields. Finally, the measurement would be performed using the ZPL, which represents every spin configuration. This possibility could be deeply studied in another future paper.
9.Conclusions
Based on the above, the NV- center is promising because of its characteristics. It is concluded that a possible candidate for solid-state qubit requires the following features:
The host lattice of the defect should show a low coupling between the system electrons and the lattice phonons (high Debye temperature) in order to work at room temperature. In addition, the lattice symmetry may be C3v with the purpose to obtain a triplet-spin system.
To have radiative transitions between different spin levels and in the case that they are degenerate, it must be possible to split them by external means (i.e., a magnetic/electric field or stress application) in order to avoid mixed states. However, the radiative transitions are not necessarily the only way, since there might be alternatives on the condition that the read-out signal presents few difficulties during the measurement.
The system must allow to be initialized, manipulated, and measured via external means.











 nueva página del texto (beta)
nueva página del texto (beta)






