1. Introduction

The technique of Stark-chirped rapid adiabatic passage (SCRAP) was first proposed in two-level quantum systems by Yatsenko et al. [¹] theoretically and then implemented experimentally [²,³]. In two-level SCRAP, two laser pulses are used in which one of them drives the population between the ground and excited states, and the other modifies the transition frequency by Stark shifting the energies of states. It is shown that two-level SCRAP can be used for the creation of the basic Pauli-X and ISWAP gates [⁴] and coherent superposition of states (half-SCRAP) [⁵]. Recently, this technique has been used to create atom-photon and atom-atom entanglement in an atom-cavity-laser system [⁶] and coherent population transfer in superconducting qubits [⁷,⁸].

The SCRAP technique was developed by Rangelov et al. [⁹] for three-level quantum systems. In this method, they used three laser pulses, one intense far-off-resonant and the others moderately strong near-resonant with atomic levels, to transfer the population between the target states. Very recently, this technique has been used for creating coherent superpositions of ground states in the interaction of a three-level atom with cavity and laser fields [¹⁰]. Three-level SCRAP technique can be a useful and efficient alternative tool for stimulated Raman adiabatic passage (STIRAP) technique [¹¹-¹⁷] in media involving multiphoton transitions. STIRAP is a popular and robust technique for complete population transfer between the ground states of a Raman-type linkage. In this technique, the Stokes pulse, linking the initially unpopulated ground state to the excited state, precedes the pump pulse, linking the initially populated ground state to the excited state (counterintuitive sequence). Provided that the two-photon resonance condition is satisfied, that there is sufficient overlap of the two laser pulses, and that the pulses are sufficiently intense, the complete population transfer occurs between two ground states without populating the excited state. In the SCRAP technique, variations in the detunings may be originated with pulse-induced dynamic Stark shifts that arise when the pump and Stokes linkages are by two-photon or multiphoton transitions. Dynamic Stark shifts are not harmful in three-level SCRAP because, as a levelcrossing technique, there is no need to maintain a resonance condition. Using suitable pulse timings, one can design an adiabatic route between initial and target states and, the unwanted population in the excited state can be minimized. SCRAP technique can be used with multiphoton transitions and dynamic Stark shifts as long as they are small compared to those produced by the Stark pulse. Stark shifts, in the SCRAP technique, modify only slightly the energy diagrams, and they have no significant effect on the population of the states. In Ref. [¹⁸], optimum control techniques have been proposed in order to optimize the standard SCRAP pulses and to minimize the decrease in fidelity brought on by inhomogeneous broadening of the transitions.

The tripod system, in which three ground states are linked by three separate fields to an excited state, has been intensely studied in quantum physics due to its connection with a wide variety of coherent quantum phenomena. STIRAP technique is extended to the tripod systems first by Unanyan et al. [¹⁹,²⁰] and experimentally demonstrated in Refs. [²¹,²²]. In tripod-STIRAP, the Λ-linkage gains an additional state coupled to the excited state by the control laser field. Tripod systems, in the resonant case, have two dark states [²³] and adiabatic evolution leads to a coherent superposition of ground states rather than to a single state.

In this work, we study the technique of Stark-chirped rapid adiabatic passage in a tripod system. In our method to reach a coherent superposition of two ground states, the pulse duration of the pump pulse (equal with the Stark pulse duration) must be larger than the pulse duration of the Stokes and control pulses, although with a smaller amplitude. With the proper timing of the laser pulses and an appropriate choice of the static detunings and peak value of the laser pulses, one can achieve a fractional population transfer between the states |1⟩( and |3⟩ with equal amplitudes, albeit with a deficient transient population in state |2⟩. Like threestate SCRAP, since the two-photon resonance condition does not need to be satisfied, we can use the tripod-SCRAP technique in the presence of multiphoton transitions and inhomogeneous broadenings. In single-photon transitions, fractional stimulated Raman adiabatic passage (f-STIRAP) [²⁴] and fractional stimulated Raman exact passage (f-STIREP) [²⁵] techniques are superior as they require far less intensity but need a precise ratio of pulse ending, which may be difficult to reach. Unlike the f-STIRAP, in tripod-SCRAP, it is not necessary for the two pulses (pump and Stokes) to vanish simultaneously. This technique is relatively robust against variations of intensities of the laser pulses, of detunings from resonances, and of the time delay between the pulses.

Our paper is organized as follows. In Sec. 2, we provide some basic definitions, equations, and construct the effective Hamiltonian of the system. Section 3 derives the general conditions for diabatic level crossings in tripod-SCRAP. In Sec. 4, we discuss the pulse timings and linkage between the target states for tripod-SCRAP. Section 5 numerically studies the sensitivity of tripod-SCRAP on the interaction parameters such as static detunings, peak Rabi frequency, spontaneous emission of the excited state, and pulse timings. Finally, the conclusions and discussions are summarized in Sec. 6.

2. Construction of the effective Hamiltonian

We consider a four-state quantum system as represented in Fig. 1. Three laser pulses couple the three long-lived ground states |1⟩, |3⟩, and |4⟩ to an excited state |2⟩. In this configuration, we assume that the states |1⟩, |3⟩, and |4⟩ (usually called ground states) are metastable, with negligible spontaneous emission in the considered time scale. The excited state |2⟩ has a relatively short lifetime due to spontaneous emission. The system is taken to be initially in the state |1⟩, and the goal is to transform it into a coherent superposition of the states |1⟩ and |3⟩ with equal amplitudes at the end of the interaction. The dynamics of the system is governed by the time-dependent Schrödinger equation (TDSE):

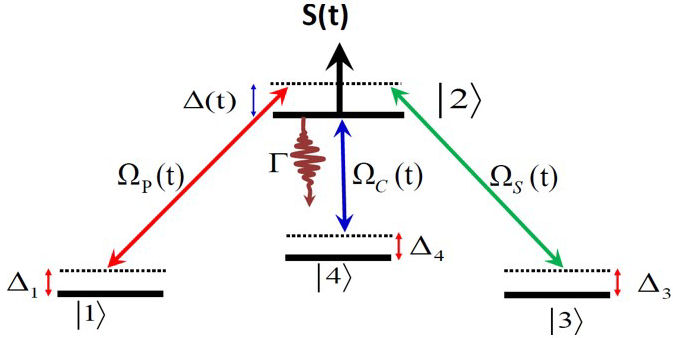
FIGURE 1 Linkage pattern scheme of the tripod-SCRAP technique. Ω _P (t), Ω _S (t), and Ω _C (t) are the pump, Stokes, and control Rabi frequencies and S(t) is the Stark pulse. ∆(t) = ∆₂ − S(t) − (1/2)iΓ and ∆ _1,3,4 are the dynamic and static detunings in which Γ is the spontaneous decay rate of the excited state (|2⟩), out of the system. 

the state vector |Ψ(t)i is a four components column-vector, whose components are probability amplitudes c(t). Using the rotating-wave approximation (RWA), the Hamiltonian for this four-level quantum system can be expressed as follows [²⁶]:

where Ω _P (t), Ω _S (t), and Ω _C (t) are, respectively, the Rabi frequencies associated with the pump, Stokes and control fields, S _ij (t) (i,j = 1,2,3,4) are the differences between the Stark shifts of the states |i⟩ and |j⟩ and the imaginary term −(1/2)iΓ describes possible population loss from state |2⟩ out of the system due to spontaneous emission and ionization. The constants ∆₂, ∆₃, and ∆₄ describe the static detunings. These detunings can arise from fluctuations in the laser frequencies and variations in the transition frequency by inhomogeneous broadenings such as Doppler shifts, which for one-photon transitions are given by:

where E ₁, E ₂, E ₃, and E ₄ are the energies of the states |1⟩, |2⟩, |3⟩ and |4⟩, respectively. The detuning shifts are the differences between the Stark shifts of the states:

For simplicity and without loss of generality, we assume that the Stark shift of the excited state (S ₂₁(t)) is negative and more significant than those of the ground states, as has been considered in Ref. [⁹]:

Using the above conditions, the Hamiltonian (2) reads:

The eigenvalues ℏεi(t) (i = 1,2,3,4) of the Hamiltonian (6) are too cumbersome to be presented here and the corresponding eigenstates of these eigenvalues (adiabatic states) are |Φ₁(t)⟩, |Φ₂(t)⟩, |Φ₃(t)⟩ and |Φ₄(t)⟩, respectively. For specific results in simulations, we shall assume the Gaussian shapes for all the pulses as follows:

where Ω₀ P, Ω₀ S, and Ω₀ C are the peak values of the pump, Stokes and control Rabi frequencies and S ₀ is the peak value of the Stark pulse, respectively. In our method, we assume that the peak values of the Stokes and control Rabi frequencies are equal to three times of the peak value of the pump Rabi frequency, Ω _0S = Ω _0C = 3Ω _0P = 3Ω₀. The center of the Stark pulse defines the time t = 0, and as such the pump, Stokes, and control pulses peak at times τ _P , τ _S , and τ _C , respectively. We take the Stokes and control pulse durations equal, T _S = T _C = T and use T as the unit of time, and (1/T) is the unit of frequency. We assume that the Stark and pump pulses have twice this duration, T _St = T _P = 2T. As an example of a real physical tripod system, we consider a beam of metastable Neon (Ne^∗) atoms crossing four well-arranged laser pulses in which the initially populated state |1⟩ (³P₀, M = 0) is coupled by a π-polarized laser pulse Ω _P (t) to an excited state |2⟩ (³P₁, M = 0), which in turn is coupled via σ ⁺ ( Ω _S (t)) and σ ⁻ ( Ω _C (t)) polarized laser pulses to the states |3⟩ and |4⟩ with magnetic sublevels of level ³P₂, M = −1 and M = +1, respectively [²¹].

Our study will follow two steps: In the first step, we will derive the general conditions for diabatic level crossings, and in the second step, we will discuss the timing between the pulses so that the population is transferred fractionally between the states |1⟩ and |3⟩ with a few transient population in the excited state |2⟩.

3. Diabatic energies and conditions for diabatic level crossings

The essential condition for the design of an adiabatic path between states |1⟩ and |3⟩ is the creation of some level crossings among the diabatic energies of the states. The diabatic energies of the states |1⟩, |3⟩, and |4⟩ are fixed because we ignore their Stark shifts. These states can only be linked adiabatically to each other when the time-varying energy of state |2⟩, crosses with them. For such level crossings, we must have:

These conditions ensure the diabatic energy of state |2⟩ crosses with the diabatic energies of the states |1⟩, |3⟩, and |4⟩, respectively. Using the above conditions, there are six level crossings. For Gaussian pulses (see Eq. (7)), the diabatic energies of states |1⟩ and |2⟩ cross at times t1,2±=±t1,2, and those of states |2⟩, |3⟩, and |4⟩ cross at times t2,3±=±t2,3 and t2,4±=±t2,4 as follows:

where T _St is the duration of the Stark pulse. By varying the laser carrier frequencies and the peak Stark value of shift S ₀, we can move the crossing points along the time axis. Complete population transfer needs appropriate settings for the interaction parameters such as the timing of the pump, Stokes, and control laser pulses relative to each other and the Stark pulse, the settings of the static detunings, and the strengths of the peak Rabi frequencies and Stark shifts. All the coherent population transfer techniques that allow us to complete population transfer between the initial and target states will also allow, in principle, to create a coherent superposition of states, provided the population transfer process stops before the completion. One of these techniques is tripod-SCRAP, which we want to use this technique to make a coherent superposition of the ground states |1⟩, |3⟩ with equal amplitudes.

4. Pulse timings and linkage between the target states in tripod-SCRAP

We assume that the conditions (8) are satisfied, the diabatic energy of state |2⟩ crosses the diabatic energies of the states |1⟩, |3⟩, and |4⟩ at the times t1,2±,t2,3±, and t2,4±, respectively.

Considering these crossings, the linkage between the states |1⟩ and |3⟩ depends on the timings of the pump, Stokes, control, and Stark pulses. These pulses cannot have the same time dependence because, as for two-state SCRAP, the complete adiabatic passage will be prevented by symmetry. Therefore, there must be some delays between the pulses. To reach a coherent superposition of two ground states and to minimize the unwanted population of the excited state |2⟩, we consider only counterintuitive pulse sequences and assume that the pump and Stokes pulses both precede the Stark and control pulses.

4.1. Counterintuitively ordered the pump and Stokes pulses (Stokes-pump-Stark-control)

In this pulse ordering, the Stokes pulse arrives slightly before the pump pulse both partially overlap with each other. Setting τS=t1,2-, τP=t2,3- and τC=t2,4+ ensures this pulse configuration. When the Stokes pulse is applied at the time t1,2-, and the pump pulse is applied at the time t2,3-, the pump pulse nearby the time t1,2- is large enough to open up the crossing between the states |1⟩ and |2⟩ and make it adiabatic and the Stokes pulse is strong enough to push the energy of the adiabatic state |Φ₃(t)i away, as no avoided crossing between the adiabatic states |Φ₂(t)⟩ and |Φ₃(t)⟩ is formed. Therefore the system, starting from the state |1⟩ initially, will evolve adiabatically through the first crossing and make a transition to the state |2⟩. Likewise, nearby the time t2,3- the Stokes pulse causes the states |2⟩ and |3⟩ cross to each other and makes it adiabatic, while at the same time, the pump pulse is strong enough to push the uppermost energy of the state |Φ₁(t)⟩ away and prevents an avoided crossing between the adiabatic states |Φ₁(t)⟩ and |Φ₂(t)⟩. The system then evolves adiabatically through the second crossing and make a transition to the state |3⟩. At the third crossing at the time t2,4-, there is almost no control laser field present, and hence the system will evolve diabatically, i.e., it will follow the diabatic state |3⟩. At the last crossing at the time t1,2+, the system will evolve adiabatically, and the population can be transferred to the state |1⟩ again, but since the intensity of the pump pulse is not strong enough, only part of the population can be transferred. In the other crossing points, given that the linking pulses are feeble, the system will evolve diabatically, and no population will be transferred between the diabatic states. Figure 2 shows the time evolution of the laser pulses, the diabatic energies of the Hamiltonian (6), and the diabatic states’ populations in the counterintuitively ordered pump and Stokes pulses, which represents a tripod-SCRAP process. This figure indicates that, by an appropriate choice of the interaction parameters such as the static detunings, adjusted through the carrier frequencies of the laser pulses, and the strengths of the peak Rabi frequencies, one can create a coherent superposition of the states |1⟩ and |3⟩ with equal amplitudes with a very small transient population in the decaying state |2⟩. The composition of the created superposition is controlled by static detunings, peak value Rabi frequencies, and robust against variations in the other interaction parameters. Furthermore, this figure indicates that unlike f-STIRAP, which requires a precise ratio of pulse ending and may be difficult to be reached in real experiments, in the tripod-SCRAP technique, it is not necessary for the laser pulses (pump and Stokes) have vanished simultaneously.

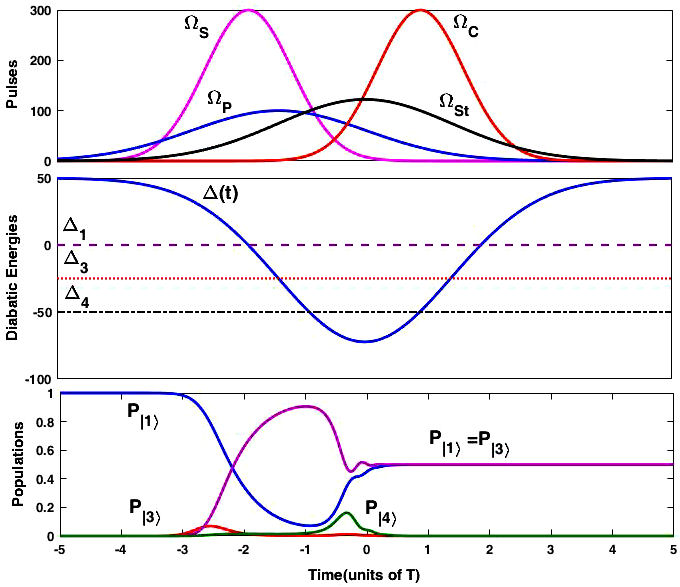
FIGURE 2 A typical example of tripod-SCRAP which leads to a coherent superposition of states |1⟩ and |3⟩ with equal amplitudes for τP=t2,3-,τS=t1,2- and τC=t2,4+. The other parameters are ∆₃ = −(1/2)∆₂, ∆₄ = −∆₂, S ₀ = 2.5∆₂, T _St = T _P = 2T, TS = TC = T, Ω0S = Ω0C = 3Ω0 = 6∆2, τS=t1,2-,τP=t2,3- and τC=t2,4+. Time evolution of the pump, Stokes, control and Stark pulse envelopes (upper frame), the diabatic energies of the Hamiltonian (6) (in units ℏ, middle frame) and the populations with counterintuitive pulse sequence, which represents a tripod-SCRAP process (lower frame). 

5. Properties of tripod-SCRAP

5.1. Sensitivity to detunings (∆₂ and ∆₄)

As discussed above, in fractional population transfer between the states |1⟩ and |3⟩ with equal amplitudes, the diabatic energy of state |2⟩ should cross the diabatic energy of states |1⟩ and |3⟩ at times t1,2± and t2,3±. The values of the detunings ∆₂ and ∆₄ are chosen to satisfy the conditions (8). The pump and Stokes pulses have to be both applied during the rising edge of the Stark pulse. In real experimental applications, detunings can change due to fluctuations in the laser frequencies and variations in the transition frequency by inhomogeneous broadening. Adiabatic passage techniques can be used to prepare quantum systems, with slowly varying parameters, in a superposition of quantum states robustly. The creation of any preselected coherent superposition of quantum states requires a robust mechanism concerning fluctuations of experimental parameters. In Fig. 3, the final fidelity of the desired state ([12](|1⟩+|3⟩)) is depicted as a function of the detunings ∆₂ and ∆₄. The figure shows that tripod-SCRAP is not sensitive against the variations of the static detunings because these changes can be compensated by dynamic Stark shifts of the diabatic energies of states and, therefore, we can use this technique in a tripod quantum system with fluctuations in the static detunings.

FIGURE 3 Final fidelity of the desired state ((1/2)(|1⟩+|3⟩)) as a function of the detunings ∆₂ and ∆₄. The other parameters are S ₀ = 125/T, Ω _0S = Ω _0C = 3Ω _0P = 3Ω₀, Ω₀ = 100/T, T _St = T _P = 2T and T _S = T _C = T. 

5.2. Sensitivity to spontaneous emission of excited state and Rabi frequency

Dissipation in the form of spontaneous emission is an important practical issue. The adiabatic passage technique is robust against the effects of spontaneous emission, as the excited state is never appreciably populated. In the tripod-SCRAP, with a counterintuitive Stokes-pump pulse sequence, the excited state is slightly populated during the adiabatic evolution of the system. Regarding this consideration, the efficiency of the population transfer decreases with increasing the spontaneous emission rate. In Fig. 4, the final fidelity of the desired state is plotted against the peak value of the Rabi frequency Ω₀ and the spontaneous emission rate of the excited state Γ, when the detunings satisfy condition (8), and the pump and Stokes pulses are applied during the rising of the Stark pulse.

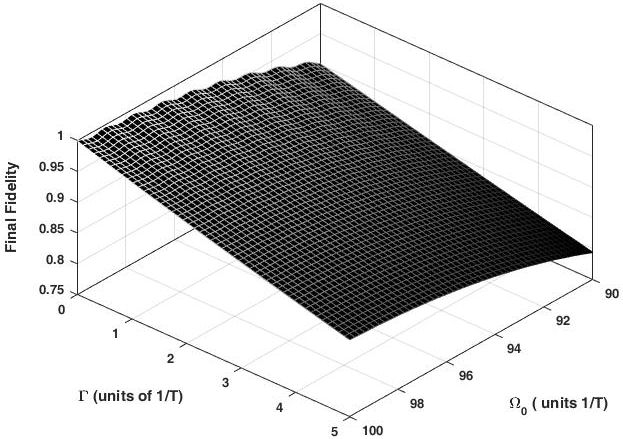
FIGURE 4 Final fidelity of the desired state ((1/2)(|1⟩+|3⟩)) as a function of the peak Rabi frequency Ω₀ and the spontaneous emission of the excited state Γ. The other parameters are ∆₃ = −(1/2)∆₂ = −25/T, ∆₄ = −∆₂ = −50/T, S ₀ = 2.5∆₂ = 125/T, τS=t1,2-,τP=t2,3-, τC=t2,4+. T _St = T _P = 2T and T _S = T _C = T. 

As shown in this figure, the final fidelity of the desired state ((1/2)(|1⟩+|3⟩)) is almost insensitive concerning small variations in laser pulses’ intensities, but it decreases with increasing the spontaneous emission rate of the excited state. Although with the increase of the peak value of the Rabi frequency (Ω₀) this effect is diminished because the excited state is almost unpopulated during the whole interaction. For sufficiently large Rabi frequency, the final fidelity of the desired state approaches unity for small-to-moderate values of the spontaneous emission of the excited state Γ, provided the adiabatic conditions at the crossing points are satisfied [⁹]. The stability of the final fidelity versus small variations in the Rabi frequency caused by intensity fluctuations, is particularly crucial for experimental implementations.

5.3. Sensitivity to pulse timings and Rabi frequency

By adjusting the timings of pump, Stokes and control laser pulses and reproduce the interaction sequence and adiabatic conditions in analogy to SCRAP, one can create, in principle, a coherent superposition of states |1⟩ and |3⟩) at the end of process. The challenge of this approach is the required high precision of the timings of the pulses. In Fig. 5, the final fidelity of the desired state ((1/2)(|1⟩+|3⟩)) is plotted against the peak Rabi frequency Ω₀ and to the timings of the pump (left side) and Stokes pulses (right side) τ _P and τ _S . This figure shows that with the parameters satisfying the adiabatic and diabatic conditions at the crossing points and an appropriate choice of the peak value of Rabi frequency ([90/T] ≤ Ω₀ ≤ [100/T]), the final fidelity of the desired state, in pulse timings intervals −1.3T ≤ τ _P ≤ −1.7T and −1.6T ≤ τ _S ≤ −2T, approaches unity. As shown in this figure, our process, in the absence of population loss, is relatively robust to variations of the pulse timings. Figure 6 shows contour plots of the final fidelity of the desired state ((1/2)(|1⟩+|3⟩)) as a function of the pump pulse τ _P and Stokes pulse τ _S positions. The upper frame represents the results in the absence of the excited state decay (|2⟩), while the lower frame shows a tripod system that undergoes spontaneous emission. Because of irreversible loss from the excited state |2⟩, out of the system, in the lower frame, the stability region (high fidelity) in the upper frame is larger than the lower frame, as shown in Fig. 6. To conclude, the technique of tripod-SCRAP has the potential to provide an efficient tool for coherent superposition of the states |1⟩ and |3⟩) without placing a sizeable transient population into the lossy state |2⟩. Therefore the tripod-SCRAP can be implemented even on time scales comparable to the lifetime of state |2⟩. However, tripod-SCRAP is not as perfect as f-STIRAP, because some population does visit the excited state |2⟩, whereas in f-STIRAP the excited state remains completely unpopulated in the adiabatic limit. Therefore, some populations will be lost in tripod-SCRAP if the lifetime of decaying state |2⟩ is shorter than the pulse durations.

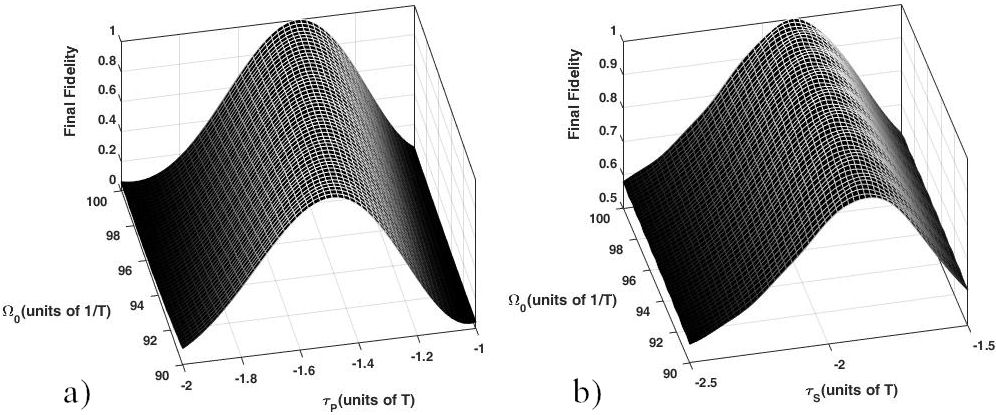
FIGURE 5 Final fidelity of the desired state ((1/2)(|1⟩+|3⟩)) as a function of the peak Rabi frequency Ω₀ and the timings of the pump (left side) and Stokes (right side) pulses τ _P and τ _S . The other parameters are ∆₃ = −(1/2)∆₂ = −25/T, ∆₄ = −∆₂ = −50/T, S ₀ = 2.5∆₂ = 125/T, T _St = T _P = 2T and T _S = T _C = T. 

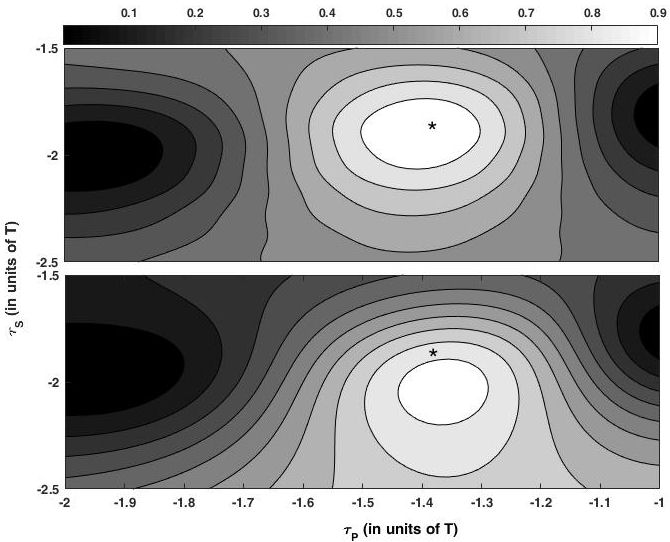
FIGURE 6 The contour plots of the final fidelity of the desired state ((1/2)(|1⟩+|3⟩)) as a function of the timings of the pump and Stokes pulses, τ _P and τ _S . Upper frame: no decay from the excited state|2⟩, Γ = 0; lower frame: decay from the excited state |2⟩ with rate Γ = 2/T. The other parameters are ∆₃ = −(1/2)∆₂ = −25/T, ∆₄ = −∆₂ = −50/T, S ₀ = 2.5∆₂ = 125/T, T _St = T _P = 2T and T _S = T _C = T. The black stars show specific values of the τ _P , τ _S used in Fig. 2 to reach a coherent superposition of two ground states (|1⟩ and |3⟩) with equal amplitudes. 

6. Conclusion

In conclusion, we have studied the SCRAP technique in a tripod system. We have shown that to make a coherent superposition of two ground states with equal amplitudes, the duration of the pump field must be larger than the pulse duration of the Stokes and control fields, although with a smaller amplitude. Many examples describe successful fractional population transfer in atom-laser systems (f-STIRAP and tripodSTIRAP); however, the best advantage of the tripod-SCRAP technique over the other adiabatic passage techniques is that the tripod-SCRAP can be used despite multiphoton transitions. These transitions are always accompanied by laser induced time-dependent Stark shifts, which destroy the two-photon resonance. In tripod-SCRAP, the Stark shifts have less destructive effects because, as a level-crossing nature of the transition mechanism, there is no need to maintain an exact resonance condition. Furthermore, the tripod-SCRAP is a powerful alternative tool for f-STIRAP and tripod-STIRAP, at least when inhomogeneous broadenings such as Doppler shifts are present. We have shown schematically, unlike fSTIRAP, in the tripod-SCRAP technique, it is not necessary for the two pulses to vanish simultaneously. This technique is robust concerning variations of intensities of the laser pulses, of static detunings, and of the time delay between the pulses.

The method we have presented here is versatile since it can be implemented in the interaction of a tripod atom with the laser pulses and cavity field for preparing atom-photon entanglement. In Ref. [⁶], using two-level f-SCRAP in an atom-cavity-laser system maximally atom-photon entangled states have been created with a coherent superposition of the atomic ground and excited states. Given that the excited state often has a short lifetime, in comparison with ground states, it is not very suitable for the creation of entangled states. In a real experiment, it is desirable that the entangled states should be as long-lived as possible, so the creation of atom-photon entangled states in the tripod-SCRAP is more efficient than two-level f-SCRAP because atom-photon entanglement can be created by a coherent superposition of the two long-lived ground states (|1⟩ and 3⟩). This technique can also be used for the creation of coherent superposition of N - 2 ground states in N-pod systems [²⁷]. For this purpose, using N - 2 Stokes pulses, with the same time dependence, and Morris-Shore transformation [²⁸-³⁰], we reduce an N-pod system to a tripod system.