1. Introduction

The “island of inversion” region around N = 20 contains Mg, Na, and Ne chains linked to the atomic mass number, A = 32 [¹]. The ³²⁻³⁶Mg isotopes, Z = 12 and N = 20-24, are worthy nuclei due to the large deformation in the ground state of these isotopes and the intruder effects. The ³²Mg nucleus has neutrons with the magic number, N = 20, meaning that the ground state is spherical, and the quadrupole moment should be small since all particles in the sd-shell are bound together. Even though the works by Détraz, Guillemaud [²] and Motobayashi, Ikeda [³] revealed that these nuclei have larger quadrupole collectively than anticipated, Wimmer, Kroll [⁴],¨ on the other hand, suggested that the 02+state is spherical and is related to pure (0p −0h) sd configurations, i.e. there is an inversion between the normal (0p − 0h) pure sd configurations and the (2p −2h) intruder configurations.

The ground state and first excited states of the ³³Mg nucleus have experimentally been described with different structures and found to have a different parity for the ground state using β-decay [^5-7]. The other structure having the same positive parity was discovered using proton inelastic scattering and Coulomb excitation [^8,9]. Similarly, a new state with unknown (J) has been observed in ³⁴Mg isotope by two separate works: P. Doornenbal [²⁴] and S. Michimasa [⁷¹]. According to the fragmentation experiments carried out and via the laser spectroscopy technique, the last structure of ³⁵Mg isotopes revealed a negative parity for the ground and first excited states [^10,11]. The level schemes for the ground state and excited states were proposed initially by Neyens [¹²]. While theoretically, it was mentioned in the shell model calculations [⁵] that the ground state has a positive parity, the shell model calculations with an SDPF-U-MIX interaction predicted an opposite parity to that of the ground state [¹³]. A separate study [¹⁴] with anti-symmetrised molecular dynamics (AMD) referred to a negative parity for the ground state and the first excited state founded on the same structure. However, the ground state of the ³⁵Mg nucleus has not been determined experimentally nor theoretically at this stage [^15,16]. The works of Watanabe, Minomo [¹⁷], Doornenbal, Scheit [¹⁸] and Gade, Adrich [¹⁹] indicate that the ground state of the ³⁶Mg nucleus is dominated by a mixture of normal and intruder configurations, i.e., mixing of (0p−0h) and (2p −2h). Consequently, this means that the ³⁶Mg nucleus can be on the border of the “island of inversion” in the Mg chain.

For the sd − pf model space, the shell model calculation relied on two types of effective interactions. First, the effective SDPF interaction [²⁰], using the full sd − pf shells for the neutrons. SDPF was reformulated to SDPF-NR [²¹] and SDPF-U [¹⁹], where the latter has two versions, one for Z ≤ 14 and N =20 to 40 with the schematic pairing (np − nh), i.e. (nℏω) sd − pf calculations so-called SDPF-U, and the other for Z > 14 called SDPF-U-Si. The schematic pairing Hamiltonian has been removed from the monopole interaction, meaning that the (np−nh) will be absent for the nuclei with Z = 15 to 20, i.e. (0ℏω) sd − pf calculations for SDPFU-Si. These two interactions are considered suitable for describing the nuclei’s nuclear structure with Z = 8 to 20 and N = 20 to 40 [²²]. A more recent version of the SDPF-U is the SDPF-U-MIX effective interaction [¹³], a mix between N=20 and N=28 in some instances. Secondly, the Monte Carlo Shell Model (MCSM) of the effective interaction of the SDPF-M [²³] utilises the full sd-shell with the f _7/2 and p _3/2 subshells of the pf model space.

A common attribute discovered in many previous theoretical studies has been the application of mixed configurations, namely, (0p −0h), (1p −1h), (2p −2h) and (3p −3h), in the full model space [²²]. Accordingly, this technique (mixed configurations) revealed the following deficiencies for SDPFM and SDPF-U-MIX interactions: (1) non-observance of the intruder states’ presence could have an impact at high excitation energy; (2) the higher excitation energy of a negative party state, which could be ascribed to the over-prediction of the excitation energy for the (2p −2h) configurations or the overestimation of the (0p −0h) and (2p −2h) mix as in the Hamiltonian SDPF-M [²⁴].

However, despite the good agreement of the first 0⁺, 2⁺, 4⁺ with the experimental results described well by most theoretical models, the higher energies remain challenging for those models. In E. Caurier’s work [¹³] (SDPF-U-MIX effective interaction), the second 2⁺ state with the energy (3 MeV) is distinctly different from the experimental result (2.558 MeV) by 0.442 MeV. Even though any indication of the third 2⁺ or the second 4⁺ states was not found in this work, some experimental works refer to these levels. Moreover, the negative parity states were higher in energy than the experimental results, similar to the values in V. Tripathi’s work [²⁵] for the ³³Mg isotopes, found the positive 1/2 and 3/2 states with the energies 0.04 and 0.12 MeV, respectively were distinctly distant from the first positive (1/2-7/2) state in G. Neyens’s work [¹²] with the experimental energy (0.546 MeV) by 0.506 and 0.426 MeV, respectively.

Furthermore, the results did not refer to the inversion between the normal (1p − 1h) and the intruder (3p − 3h), as mentioned in V. Tripathi’s work [²⁵]; it only made mention to (3p−3h) intruder configurations. As such, these reasons (deficiencies of mixed technique) have motivated the researchers to embrace another technique such as the truncations of the model space similar to the work of F. Mare’chal et al., [²⁶] that truncates the sd−pf model space to the sd model space and only f _7/2 and p _3/2 shells of the pf model space to reduce the dimensionality of the calculations for ³¹Mg and ³¹Al. Further to the truncation, other works by Kimura [²⁷], Kimura [¹⁴] and Momiyama et al. [¹⁶] utilised the unmixed (0p −0h) (1p −1h), (2p −2h) and (3p −3h) configurations to explain the structure of the ³¹Mg, ³³Mg and ³⁵Mg nuclei using the AMD model with a Gogny interaction.

Two phenomena may cause a reduction in the N = 20 shell gap: (1) the nucleon-nucleon residual interaction, particularly the monopole proton-neutron interaction, known as a “spin-flip” or spin-isospin interaction, and (2) the tensor (non-central) interaction, also responsible for shifting the energies of the nuclear levels (subshells) [^28-35]. In other words, two interactions affect the size of the N = 20 gap and, concurrently, depending on the number of protons in the subshell d _5/2. The first interaction is the attraction between the subshells d _5/2 and d _3/2, and the second interaction is the repulsion between the subshells d _5/2 and f _7/2. When the d _5/2 is full or semi-full, the interactions are very strong; therefore, the shell gap will be wide, preventing the neutrons from moving across this gap. While for those interactions that are very weak, when it is empty or semi-empty, and the shell gap will be narrow, then the neutrons will be able to cross this gap, as illustrated in Fig. 1.

FIGURE 1 Spin-flip and tensor interactions effects. 

The restricted configuration is a common technique often employed to solve the island of inversion problems. In 1998, R. W. Ibbotson et al., used the restricted configurations of neutrons (d _5/2)⁶ (d _3/2,s _1/2)⁴ (f _7/2p _3/2)² for ³²Mg nucleus for (np−nh) with n = 2 only [³⁶]. Similarly, Pritychenko et al., employed the restricted configurations of protons (d _5/2)³ (d _3/2,s _1/2)⁰ and (d _5/2)² (d _3/2,s _1/2)¹ for the ³¹Na nucleus [³⁷]. However, in a separate study, T. Siiskonen et al. applied the restriction method for unmixed (0p −0h) and (2p −2h) [³⁸]. Similarly, the ground state of the ³¹Mg nucleus has been established from Yordanov et al. by assuming the restriction for neutron space (sd − f _7/2,p _3/2) and for proton space (d _5/2)² (d _3/2,S _1/2)² with mixing (0.1 and 2) ℏω [¹¹].

According to the new outputs (spin-flip and tensor interactions effects) discussed above, none of these restrictions considers the positions of the protons with the unmixed (1p −1h), (2p,2h), (3p −3h) which is critically important in producing high correlation energy to reduce the energy of the N = 20 shell gap.

In the present work, the SDPF-U interaction under restricted configurations was used with the OXBASH code [³⁹] to investigate the nuclear structure of the ³²⁻³⁶Mg isotopes. Using restricted configurations provides the best correlation energy required for vanishing the N = 20 shell gap. The work of this study further aimed to investigate the effects of the unmixed (1p −1p), (2p −2h), (3p −3h) intruder configurations and demonstrate the precision in the application of the Hamiltonian predictions under this restriction.

2. Shell model calculations

In this work, the calculations were based on restrictions to the configurations of the nucleons in the model space. The restrictions were made in order to (i) reduce the attraction of the spin-flip interaction between the πd _5/2 and vd _3/2 subshells and to reduce the repulsion tensor interaction between the πd _5/2 and vf _3/2 subshells; (ii) to reduce mixing between the (0p−0h) normal configurations and the (2p−2h) intruder configurations in the ground state and excited states, and mixing between the (1p −1h) and (3p −3h) configurations for the excited state only; and (iii) to reduce the dimensionality of the calculations due to the difficulty of diagonalizing the Hamiltonian precisely in a wide model space [²⁶].

2.2. Even-even Mg nuclei

This section presents the results for the 32,34,36Mg isotopes. According to the shell model, the ground state of ³²Mg has a closed ¹⁶O core, with 16 nucleons, namely, four protons and 12 neutrons, in the sd model space. The ground states for these isotopes are considered within the (2p−2h) configuration.

2.2.1. The case of ³² Mg isotope

The restricted configurations used to calculate the energy levels of the ³²Mg nucleus are illustrated in Fig. 2 below. Three kinds of configurations were proposed, (1p−1h), (2p−2h) and (3p −3h), and were considered separately, though they relied on the same ground state. Two protons in πd _5/2 and two protons in πS _5/2 subshell were proposed for the even intruder configurations (2p−2h) of neutrons while two protons in πd _5/2 and two protons in πd _3/2 subshell were proposed for the odd intruder configurations (1p −1h) and (3p −3h) of neutrons.

FIGURE 2 (Colour online) Restricted configurations used in calculations for ³²Mg nucleus. 

Accordingly, the positive parity states were predicted with the (2p−2h) configurations. Figure 3 below displays the comparison between the values calculated using the SDPF-U interaction and the available experimental data and the previous theoretical values with different interactions. The levels with “( )” refer to the assignment and/or the parity of the states that were poorly established through the experiments.

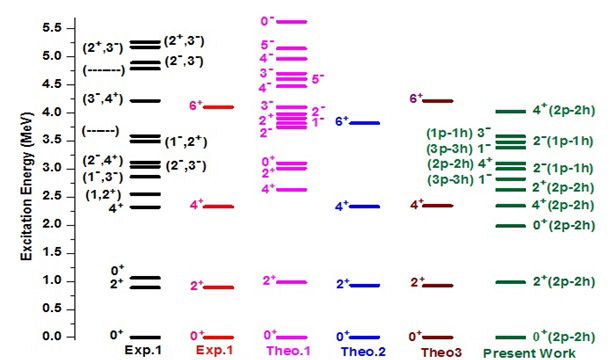
FIGURE 3 (Colour online) Positive and negative states with SDPF-U Hamiltonian under restriction compared with available experimental data taken from [^40,41] and theoretical results taken from [^25,41,42], respectively for the ³²Mg nucleus.  

As illustrated in Fig. 4, good agreement was revealed between the first excited state 2⁺ ₁ at 0.98 MeV with the experimental data [^40,41] and previous theoretical works [^25,41,42]. The calculations further revealed that there is an energy at 1.98 MeV belonging to the 0⁺ ₂ This energy is the best compatible value to the experimental value of 1.058 MeV [^40,43], more than the theoretical value in Ref. [⁶¹]. The excited state predicted with J=41+and energy of 2.34 MeV appeared to be compatible with the experimental state with J=41+, energy of 2.32 MeV [^40,41] and the shell model calculations [^41,42]. The calculations revealed a preference for the state with J=22+at an energy level of 2.62 MeV, which was in better agreement with the experimental data [⁴⁰] than the (MCSM) calculations [²⁵].

FIGURE 4 (Colour online) Restricted configurations used in the calculations for ³⁴Mg nucleus. 

The present work also revealed that the prediction of the states with J=42+at the energy levels of 3.1 and 4.02 MeV were close to the experimental values at 3.117 MeV and 4.215 MeV, respectively, having been found with tentative J values [⁴⁰]. On the other hand, in our calculations, the predictions were not very distinct nor clear above the energy 4.02, i.e. (6⁺ ₁ state at the energy in Ref. [⁵⁹] and 3.1 MeV in Ref. [⁶¹] in addition to the (2⁻ ,2⁺ ,3⁻), (2⁺ ,3⁻) and (2⁺ ,3⁻) states at the energies of 4.819 MeV, 5.169 MeV and 5.203 MeV respectively in Ref. [⁵⁸]). The negative parity states were identified using two types of configurations: the normal (1p−1h) configuration and the intruder (3p−3h) configuration, adopting the same ground state.

According to V. Tripathi et al. [²⁵], the states with energy levels of 2.858 and 3.037 MeV are expected to have a negative parity. However, there will also be uncertainty in the determination of the spin. The state with experimental energy of 2.858 MeV [⁴⁰] was identified as the theoretical state with J = 1⁻ in the calculation. The prediction showed that J = 2⁻ at an energy level of 3.05 MeV was the closest to the experimental data with J = 2⁻ , 3⁻ at an energy level of 3.037 MeV [⁴⁰]. Similarly, the energy level at 3.553 MeV was shown to agree with the negative parity state in the calculations with J = 2⁻ at 3.5 MeV

Transition probabilities are considered as one of the most sensitive parameters in the evaluation of effective interactions. Therefore, to evaluate this sensitivity, the reduced electric quadrupole transition probability, B(E2) and the deformation parameter (β2), were calculated. The theoretical and experimental values of B(E2) (in units of e²fm⁴) for the transition of (01+→21+) and the β2 values for the ³²Mg isotope are depicted in Table I. Compared to the previous work, the values exhibited acceptable agreement, especially if the error percentage was considered.

2.2.2. The case of ³⁴ Mg isotope

Figure 4 illustrates the presupposed structure of the ³⁴Mg nucleus with the restricted configuration, where the configuration was used to predict the energy levels of this nucleus. The proposed positions of protons were two protons in πd _5/2 and two protons in πS _5/2 subshell for the even intruder configurations (2p −2h) of neutrons.

As shown in Fig. 5 below, the comparison with the available experimental data [^18,53,54] showed a good agreement for the ground and excited states, J=21+and J=41+, of the ³⁴Mg nucleus. Moreover, the Refs. [^18,54] showed an excited state with the energy levels of 3.13 and 3.19 MeV, respectively, with unknown J values. According to the calculations, the coincidental theoretical state was J=42+ at an energy level of 3.24 MeV in the study by Nowacki and Poves [²²], who used the SDPF-U interaction to calculate the energy level of the ³⁴Mg nucleus. However, the results of the current study were more consistent with the experimental values, as shown in Fig. 6. In fact, the consistency demonstrated the importance of the restricted configuration. Further support was also shown for the calculations through the B(E2) values. Likewise, the comparison with the available experimental and theoretical values showed an apparent convergence, especially with the referenced result [⁴⁷], as illustrated in Table 2.

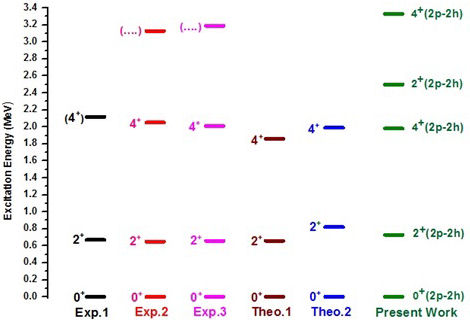
FIGURE 5 (Colour online) Energy states with SDPF-U Hamiltonian under restriction (2p − 2h) compared with available experimental data taken from [^18,53,54] and theoretical results are taken from [^22,42], respectively for the ³⁴Mg nucleus. 

FIGURE 6 Restricted configurations used in calculations for the ³⁶Mg nucleus. 

2.2.3. The case of ³⁶ Mg isotope

Accordingly, three exited states were found for the ³⁶Mg nucleus [^18,19,54], where the proposed restricted configuration in this work is shown in Fig. 6. The proposed positions of protons were two protons in πd _5/2 and two protons in πS _5/2 subshell for the even intruder configurations (2p − 2h) of neutrons.

The experimental and theoretical energy spectra for ³⁶Mg are shown in Fig. 7 below, in which comparison is made between the theoretical and experimental values, showing an agreement for the first excited state with J=21+. The calculations confirmed the J value of the excited state at an energy level of 1.95 MeV. This state was also present in [¹⁸] with J = 4⁺, while Michimasa et al., [⁵⁴] included this state with an unknown J value. In this work, the state with J = 4⁺ at an energy level of 1.94 MeV was predicted, which appears to be the closest to it. Moreover, the calculated B(E2:0⁺ → 2⁺) value of ³⁶Mg showed good agreement with the experimental values similar to the B(E2:0⁺ → 2⁺) values for the ³²Mg ³⁴Mg nuclei. Table III displays the comparison between the calculated transition probability and the available experimental and theoretical values.

FIGURE 7 Energy states with SDPF-U Hamiltonian under restriction (2p − 2h) compared with the available experimental data taken from [^18,19,54] and theoretical results taken from [^22,23], respectively for the ³⁶Mg nucleus. 

2.3. Even-Odd Mg nuclei

Two isotopes with odd neutron numbers, namely ³²⁻³⁶Mg and ³⁵Mg were also considered in this work. The same rules of the ground state in 32,34,36Mg isotopes are considered for the ground state of ^33,35 Mg isotopes, i.e., the ground states for these isotopes are considered within the (2p−2h) configuration.

2.3.1. The case of ³³ Mg isotope

The proposed distributions of the ³²⁻³⁶Mg nucleus are illustrated in Fig. 8 below, where three configurations were adopted (1p −1h), (2p −2h) and (3p −3h), based on the same ground state. Two protons in πd _5/2 and two protons in πS _5/2 subshell are proposed for the even intruder configurations (2p − 2h) of neutrons while two protons in πd _5/2 and two protons in πd _3/2 subshell are proposed for the odd intruder configurations (1p−1h) and (3p−3h) of neutrons.

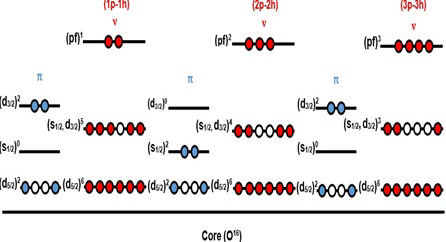
FIGURE 8 (Colour online) Restricted configurations used in the calculations for the ³²⁻³⁶Mg nucleus. 

Previous experimental works have highlighted inconsistencies regarding the identification of the ground states of this nucleus, such as J = 3/2⁺ from the works of [^5-7], J = 5/2⁺ from the works of [^8,9], and with J = 3/2⁻ from the works of [^10-12].

The predictions in this current study for the ground state of the island of inversion nuclei were dominated by the (2p−2h) configurations. According to this assumption, three particles in the pf-shell give a negative parity for the ground state in which this configuration assigns the ground state of ³²⁻³⁶Mg with J = 3/2⁻ which is consistent with the experimental results from [^10,12]. The first excited state was found experimentally with J = 5/2⁻, where the calculations predicted this state with J = 5/2⁻ at an energy level of 0.534 MeV, as reflected in Fig. 9. The experimental work of G. Neyens [¹²] noted a state with an uncertain J = 1/2⁺ − 7/2⁺ at an energy level of 0.546 MeV. Nonetheless comparing these findings with the results of this current work, the nearest theoretical state was J = 3/2⁺ at an energy level of 0.62 MeV. Moreover, the theoretical state with J = 5/2⁺ and energy of 0.733 MeV confirmed the presence of the experimental state, also demonstrated from the work of G. Neyens [¹²], without a J value at an energy level of 0.705 MeV, and also from that of A. L. Richard et al., [¹⁰] with J = 1/2⁺ ,3/2⁺ ,5/2⁺ at an energy level of 0.703 MeV.

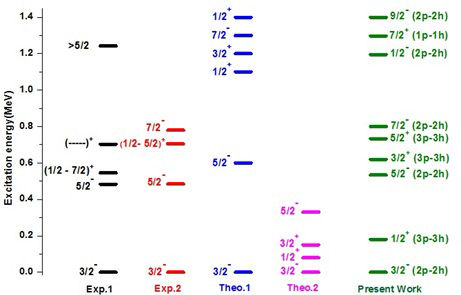
FIGURE 9 (Colour online) Energy states with SDPF-U Hamiltonian under restriction compared with the last available experimental data taken from [^10,12] and theoretical results taken from [^13,14], respectively for the ³²⁻³⁶Mg nucleus. 

The fourth excited state from the work of A. L. Richard [¹⁰] with J = 7/2⁻ at an energy level of 0.78 MeV was shown to have an equivalent theoretical state from the calculations with J = 7/2⁻ and energy of 0.8 MeV. The last energy state, found experimentally by G. Neyens [¹⁸] at an energy level of 1.243 MeV, showed a good agreement with the theoretical state from this work with J = 7/2⁺ and an energy level of 1.29 MeV. Our calculations predicted a new state for 1/2⁺ at 0.180 MeV; this prediction supports the notion of the positive parity state above the ground state as in Ref. [¹⁹]. In addition, we have new predicted states (1/2, 7/2 and 9/2 at the energies of 1.195, 1.297 and 1.399 respectively) to explore experimentally.

2.3.2. The case of ³⁵ Mg isotope

Figure 10 below illustrates the distributions for the ³⁴Mg nucleus used in the calculations where the configurations were (1p−1h) and (2p−2h). Two protons in πd _5/2 subshell and two protons in πS _5/2 subshell were proposed for the even intruder configurations (2p−2h) of neutrons while two protons in πd _5/2 subshell and two protons in πd _3/2 subshell were proposed for the odd intruder configurations (1p − 1h) of neutrons.

FIGURE 10 (Colour online) Restricted configurations used in the calculations for the ³⁴Mg nucleus. 

The ground state was identified in this work with J = 7/2⁻. This prediction seemed to be identical to the results by S. Watanabe et al., [¹⁷]. As shown in Fig. 11, the first excited state was found with an uncertain J = 5/2⁻ ,7/2⁻ at an energy level of 0.206 MeV from the work of S. Momiyama et al., [¹⁶]. According to the calculations in this study, the first excited state was found with J = 5/2⁻at an energy level of 0.171 MeV. Furthermore, similar to the ³²⁻³⁶Mg isotope, our calculations revealed a positive parity state with J = 1/2⁺ at 0.21 MeV which is back to the configurations (1p−1h), and back to the (3p −3h) configurations in ³²⁻³⁶Mg.

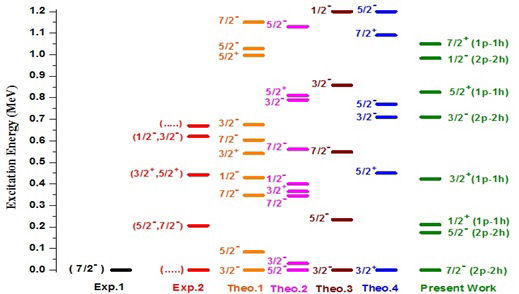
FIGURE 11 (Colour online) Energy states with SDPF-U Hamiltonian under restriction compared with available experimental data taken from [^16,17], respectively and theoretical results, Theo.1 and Theo.4 taken from [¹⁶], and Theo.2 and Theo.3 taken from [¹⁵] for the ³⁴Mg nucleus. 

Also, the calculations using the SDPF-U Hamiltonian confirmed the experimental J value of the doublet consisting of states at an energy level of 0.443 MeV [¹⁶] with J = 3/2⁺ at an energy level 0.423 MeV. For the next experimental excited state at the energy 0.616 with uncertain J=1/2+,3/2-, our calculations give the assignment J = 3/2 at the energy 0.711 MeV which is compatible with the previous theoretical works by [¹⁶]. Finally, the energy level at 0.670 was reported by [¹⁶] having an unknown J value. In this current study, our prediction suggested the positive parity assignment J = 5/2⁺ within the (1p − 1h) configurations which is compatible with the predicted assignment in Ref. [²³].

3. Summary and Conclusions

The effects of intruder configurations were investigated in this study using the SDPF-U Hamiltonian with a specific nuclei distribution in the island of inversion N = 20 region. The study was based on calculating the energy states and the reduced electric quadrupole transition probabilities of the Mg chain isotopes. This was in addition to the best (protons and neutrons) configurations that provided good correlation energy necessary to reduce the N = 20 shell gap. The results were then compared with recently available experimental data.

The best agreement between the experimental and theoretical results for positive ground states and excited states _of ^32.34,36 Mg isotopes and the negative ground states of ^33,35 Mg isotopes was found when the proposed (2p − 2h) neutrons configurations were (s _1/2, d _3/2)⁻², (f _7/2, p _3/2)⁺2 and protons configurations were (d _5/2)⁻² ,(s _1/2)⁺². While the best agreement between the experimental and theoretical results for the negative excited states of ³²Mg isotope was found when the proposed (1p − 1h) and (3p − 3h) neutrons configurations were (s _1/2,d _3/2)⁻¹, (f _7/2,p _3/2)⁺¹ and (s _1/2,d _3/2)⁻³, (f _7/2,p _3/2)⁺³, respectively, and when the protons configurations were (d ^5/2 )⁻², (d _3/2 )⁺².

For the positive excited states of the ^33,35 Mg isotopes the best agreement between the experimental and theoretical results was found when the proposed (1p −1h) and (3p −3h) neutrons configurations were (s _1/2,d _3/2)⁻¹, (f _7/2,p _3/2)⁺¹ and (s _1/2,d _3/2)⁻³, (f _7/2,p _3/2)⁺³, respectively, and protons configurations were (d _5/2)⁻², (d _3/2)⁺² for ³³Mg. While for ³⁵Mg isotopes, it was found when the proposed (1p − 1h) neutrons configurations were (s _1/2,d _3/2)⁻¹, (f _7/2 ,p _3/2 )⁺¹ and protons configurations were (d _5/2)⁻², (d _3/2)⁺². The calculations of the positive parity states of the 32,34,36Mg nuclei were linked with the (2p −2h) configurations, while linked with the (1p−1h) and (3p−3h) configurations in the ^33,35 Mg nuclei. Also, contrary to the negative parity states in the ³²Mg nucleus linked with the (1p −1h) and (3p −3h) configurations, it was linked with (2p−2h) configurations in ^33,35 Mg.

Accordingly, these outcomes confirmed the existence of the intruder (1p −1h) and (3p −3h) configurations, along with an inversion found between them. Furthermore, the calculations administrated determined that the intruder configuration of (3p −3h) did not exist in the ³⁵Mg nucleus. Indeed, this outcome may position this nucleus as a border of the N = 20 island of inversion region from the right side for odd Z. The calculations also showed the possibility to use the SDPF-U Hamiltonian with unmixed configurations in the N = 20 island of inversion region. This appropriation appeared through the significant agreement between the theoretical and experimental results for the ³²⁻³⁵Mg nuclei energy states. In this case, the SDPF-U calculations confirmed numerous energy states in the ³²⁻³⁵Mg energy spectrum and suggested J values for others.

In summary, there is a requirement to use this effective interaction (SDPF-U Hamiltonian) with the odd-even nuclei and odd-odd nuclei. The good outcomes of our calculations for the transition probabilities showed that the unmixed configurations along with the positions of protons play an important role in the binding of energy of the ground state, which led to good, calculated values of the transition probabilities B(E2: Jfirst excited state → Jground state) values, i.e., the shape of the nucleus in the ground state.