1.Introduction
Many fields of physics benefit from the nonlinear partial differential equations (NPDEs) in a wide variety of applications to mechanics, electrostatics, quantum mechanics, and finance. In linear theory, solutions usually have representation formulas and conform to the superposition principle. Despite some equations governing nature were recognized to be linear since the 19th century, this advance was widely criticized in the 20th century. It is possible to observe NPDEs not only in non-Newtonian fluids, glaciology, rheology but also in stochastic game theory, nonlinear elasticity, flow through a porous medium, and image-processing. As a result, no available superposition can be found for nonlinear equations; therefore, there is a need for studying those equations. Over the last few years, a crucial number of new methods have been proposed to obtain exact solutions for NPDEs. The Davey-Stewartson equation (DSE) has been studied in many areas of research such as chemical engineering, nonlinear mechanics, biology, and physics. To define the evolution of a three-dimensional wave packet in finite depth water, Davey-Stewartson (1974) had presented the DSE in his research study about fluid dynamics1.
In (2+1)-dimensions, the Davey-Stewartson equation is known as a solution equation
that examines long and short wave resonances and other wave propagation patterns.
For more details, we refer to the previous research works conducted in Refs. 2-3. The Davey-Stewartson theory is an NPDE for a
complex field (wave-amplitude) q and a real field (mean flow)
This important system of equations has attracted the attention of many researchers.
For example, the line soliton 4,
the semi-inverse variational principle method (SIVPM), the improved
In Ref. 44, Ghanbari and his collaborator developed an efficient methodology for obtaining exact solutions to NPDEs which is known as a generalized exponential rational function method (GERFM). The authors applied the technique to solve the resonant nonlinear Schrödinger equation (R-NLSE). It has been proven over time that the method enables us to be implemented in many different NPDEs arising in mathematics, physics, and engineering 45-54. The proposed method reproduces many types of precise solutions, and it is very useful for finding the exact solutions of the equation with relative ease. Recently, a new version of the method for solving partial differential equations with local fractional derivatives has been considered in Ref. 55,56.
In this paper, the GERFM is used to solve the Davey-Stewartson equation. This paper consists of the following parts: In Sec. 2, we introduce the methodology of the GERFM. In Sec. 3, the results of using the method in determining the solutions of the equation (according to the main achievement of this article) will be presented. Finally, the article ends with some concluding remarks.
2.Methodology of the GERFM
The technique is a very efficient method in solving partial differential equations 44. The basic steps of using this method are listed below.
1.NPDE will be accepted as follows:
To abbreviate the NPDEs is the following ordinary differential equation (ODE), it
will be used
2.The crucial part of the new methodology comes from the fact that Eq.(2.2) has the formal solution of
where
The real (or complex) unknown constants are
Also, it is essential to determine the positive integer m by the principle of balancing.
3.By adding all terms and inserting Eq. (2.3) into Eq.(2.2), the left-hand side of
Eq.(2.2) is converted into the polynomial equation
4.Finally, exact solutions to Eq.(2.1.) are derived through solving the algebraic nonlinear system of equations in step 3.
3.The results
The first step is the traveling wave transformation of Eq.(1.1) by utilizing the following new variables
and
In addition, constants of μ, η, α, and β should be determined. Using the wave
transformation of Eq.(3.1) and Eq.(1.1) together with
Integrating Eq. (3.4), we obtain
Substituting Eq.(3.5) in Eq.(3.3) will turn into the following nonlinear differential equation:
where primes denote the derivatives with respect to
By following the described methodologies in section 2, we obtain several non-trivial solutions of (1.1).
Family 1: We attain the results for p = [1,1,-1,1] and q = [1,-1,1.-1], which gives
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution was reached for Eq.(1.1):
Case 2:
We have replaced the above values with Eqs. Eq.(3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Case 3:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for (1.1):
Figure 1 shows the dynamic behavior of modulus
of solutions

Figure 1 Dynamic behaviours modulus of solutions q3 (x; y; t) (left) and φ3 (x; y; t) (right) for δ = 1:05; γ = 1:3; a = β = 0:5; λ = 1:5; and t = 1.
Family 2: We attain the results for p = [i,-1,1,1] and q = [i,-i,i-i], and thus one gets
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Case 2:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Figure 2 shows the dynamic behavior of modulus
of solutions
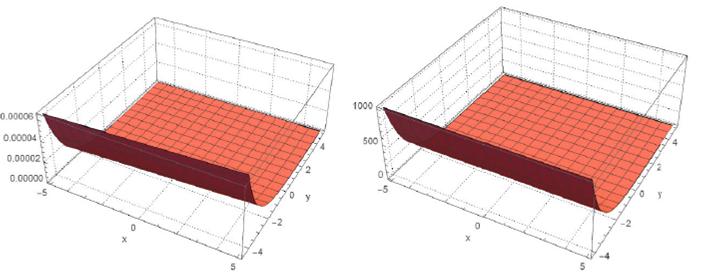
Figure 2 Dynamic behaviours modulus of solutions q 5 (x; y; t) (left) and φ5 (x; y; t) (right) for B 1 = 1; δ= 8:5; γ = 2:01; λ = 4:25; ¸ = 0:92; and t = 1.
Case 3:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for equation (1.1):
Family 3: We attain p = [1,1,-1,1 ] and q = [2,0,2,0 ], which gives
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Case 2:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Figure 3 shows the dynamic behavior of modulus
of solutions
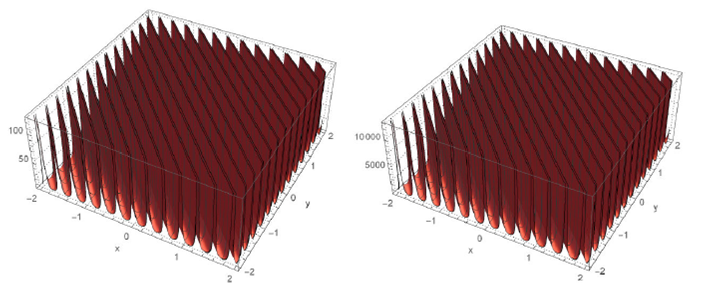
Figure 3 Dynamic behaviours modulus of solutions q 8 (x; y; t) (left) and φ8 (x; y; t) (right) for A 1 = 1; δ = 1:01; γ = 2:3; λ = 0:2; ¸ = 0:5; and t = 1.
Family 4: We attain the results for p = [-1,3,1,-1 ] and q = [2,0,2,0 ]. So, it reads
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for equation (1.1):
Case 2:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for equation (1.1):
Family 5: We attain the results for p = [-1,1,1,1 ] and q = [1,-1,1-1 ], which gives
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Figure 4 shows the dynamic behavior of modulus
of solutions
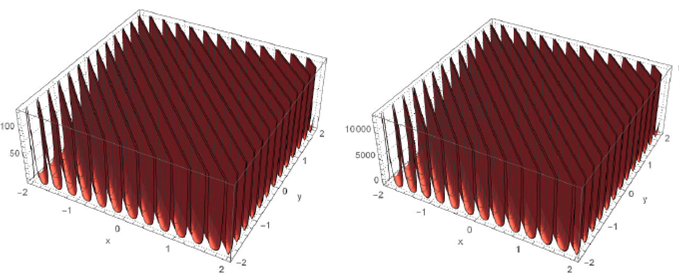
Figure 4 Dynamic behaviours modulus of solutions q 11 (x; y; t) (left) and φ11 (x; y; t) (right) for A 1 = 1; δ = 1:01; γ = 2:3; a = 0:2; λ = 0:5; and t = 1.
Family 6: We attain the results for p = [-1-i,1-1,-1,1 ] and q = [i,-i,i-1 Α, and one obtains
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Family 7: We obtain p = [-2-i,2-i,-1,1 ] and q = [i,-i,i,-i ], and thus one attains
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for equation (1.1):
Family 8: We attain the results for p= [1-i,-1-i,-1,1 ] and q= [i,-i,i,-i ], and thus we obtain
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Family 9: We attain the results for p= [ -3,-1,1,1 ] and q= [ 1,-1,1,-1 ], and thus we have
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq. (1.1):
Family 10: We attain the results for p= [ -2-i,-2+i,1,1 ] and q= [ i,-i,i,-i ], and thus one has
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for Eq.(1.1):
Figure 5 shows the dynamic behavior of modulus
of solutions

Figure 5 Dynamic behaviours modulus of solutions q 16 (x; y; t) (left) and φ16 (x; y; t) (right) for A 0 = 1; δ = 1:1; γ = 0:8; a = 0:9; λ = 0:2; and t = 1.
Family 11: [F11] We attain the results for p= [ 1-i,1+i,1,1 ] and q= [ i,-i,i,-i ], and then one results
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution was reached for Eq. (1.1):
Figure 6 shows the dynamic behavior of modulus
of solutions

Figure 6 Dynamic behaviours modulus of solutions q 17 (x; y; t) (left) and φ17 (x; y; t) (right) for A 1 = 1; δ = 1:5; γ = 0:5; a = 0:1; λ = 0:2; and t = 1.
Family 12:
We attain the results for p= [ -3,-2,1,1 ] and q= [ 0,1,0,1 ], and we get
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for equation (1.1):
Figure 7 shows the dynamic behavior of modulus
of solutions
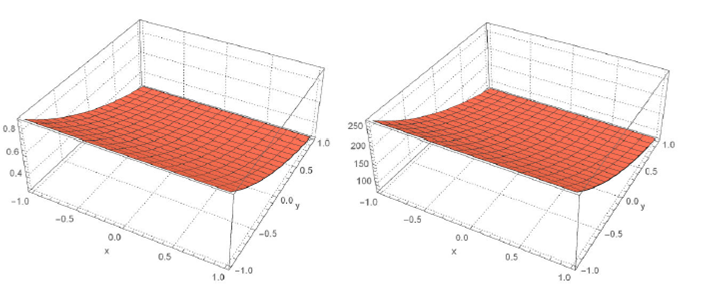
Figure 7 Dynamic behaviours modulus of solutions q 18 (x; y; t) (left) and φ18 (x; y; t) (right) for A 1 = 1; δ = 5; γ = 0:1; a = 1.5; λ = 0:3; and t = 1.
Family 13:
We attain the results for p= [ -1,-2,1,1 ] and q= [ 1,0,1,0 ], and one finds
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for equation (1.1):
Family 14: We attain the results for p= [ 2,1,1,1 ] and q= [ 1,0,1,0 ], and then we obtain
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for equation (1.1):
Family 15: We attain the results for p= [ -1,0,1,1 ] and q= [ 0,0,1,0 ], and then we find
Case 1:
We have replaced the above values with Eqs. (3.7) and (3.8) together with (3.5)
Hence, the following exact solution has been reached for equation (1.1):
Figure 8 shows the dynamic behavior of modulus
of solutions

Figure 8 Dynamic behaviours modulus of solutions q 21 (x; y; t) (left) and φ21 (x; y; t) (right) for A 0 = 1; δ = 2; γ = 0:9; β = 0.5; λ = 0:7; and t = 1.
Remark 1 In each of the above cases, we take
4.Conclusion
Partial differential equations have many applications in modeling practical problems in our lives. This importance has created additional motivation for researchers to develop new and efficient methods. Some of these techniques enable us to achieve exact solutions to such problems. However, determining such solutions is impossible or very difficult for some categories of equations. The method used in this paper, called the GERFM, is a powerful technique to determine the exact solutions to different types of PDEs. In this survey, the method has been utilized to solve the Davey-Stewartson equation. It was shown that the method is a suitable technique to solve the Davey-Stewartson equation with this study. The results are quite reliable for solving this problem. Further, we believe that the presented methods and results in this paper are valuable to all researchers in the field of mathematical physics. Therefore, GERFM offers an excellent opportunity for future research studies on related topics of the research. This emphasizes the power of the method used in providing exact solutions to various real-world applied models.











 nueva página del texto (beta)
nueva página del texto (beta)


