nueva página del texto (beta)
Inglés (pdf)
Artículo en XML
Referencias del artículo
Traducción automática
Enviar artículo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. Introduction
This principal idea of this article is focused on proposing the optical solution to the GFLM “which makes revolution in the social media”. The suggested model is the important one that appears in the area of nonlinear optical fibers and represents the power low nonlinearity from which the FLM with its different forms are emerged. Moreover, this model plays a vital rule in many complex nonlinear phenomena, including acoustics, nonlinear optics, telecommunication industry, convictive fluids, plasma physics, condensed matter, and solidstate physics. Specially, this model represents the propagation of short light pulses in the mono-mode optical fibers. Various authors have studied the FLM via different methods [19-30]. On the other hand, the GFLM will be discussed for the first time in the frame work of two distinct techniques namely the MSEM and the RPSODM. The suggested methods have been examined previously for many NLPDE and achieved good results. The suggested two methods belong to the well-known ansatz methods. The MSEM surrenders to the balance rule and achieve analytical closed form solution while the RPSODM is the only one of the ansatz methods which does not surrenders to the balance rule and reduces the volume of calculation and continuously achieve impressive results. The two methods are applied in the same vein and parallel. The suggested equation is in fact mainly responsible of a surprising representation for all modern social media arising in the soliton technology. Furthermore, recent studies for new significant models have been demonstrated for just few authors, for example, Khan and Atangana [31] who describe the mathematical modeling and dynamics of a novel corona virus (2019-nCoV), specially the brief details of interaction among the bats and unknown hosts, then among the peoples and the infections reservoir, and Khan, et al. [32] who regarded on of the reason for lever inflammation and explores the HEV dynamics in fractional derivative.
According to [10, 22], GFLM can be written as,
Here, p(x;t) is a complex-valued function which represents the temporal development of the pulses. Furthermore, the variables b, σ are the self -phase modulation and the nonlinear dispersal respectively, while α 1, α 2 are the group velocity dispersal and the spatial-temporal dispersal respectively. In addition, α is the influence of the considered dispersal, λ is the special effect of deepening and µ captures the effect of nonlinear dispersal. Finally, n denotes the generalized full nonlinearity. Recently, many approaches have resulted in the exact solutions to NLPDEs which are mostly demonstrated through [1-18]. One of the most famous and powerful ansatz methods which is described briefly and results in the closed form optical solutions for the NLPDEs is the MSEM. In the same vein and parallel, the RPSOM which treats the frailer of balance operation significantly and satisfies the optical solitons exactly has been used.
2. Applications
In this section, the modified simple equation method is applied on the suggested equation in order to find the optical solutions. In terms of some parameters, the travelling wave solutions are achieved when these constants are determined.
2.1.The closed form solution using the MSEM
According to the MSEM, the solution is written as:
where A k (0 ≤ k ≤ m) are arbitrary constants and A m 6= 0. The unknown function ψ(ζ) is determined by finding arbitrary constants and we have ψ’(ζ) 6= 0. The positive integer m is derived by using the homogeneous balance between the nonlinear term and the highest order derivative term. A function of ψ −j (j = 0,1,2,....) is achieved by computing the derivative of the function R(ζ). By setting the same powers of ψ −j to zero, we will organize the system of algebraic equations. The constants A k appearing in this system can be determined using any organized computer program such as Maple or Mathematica software. Now, for the suggested equation this wave transformation is introduced:
where ζ = x − vt denotes to the shape features of the wave pulse, θ(x,t) = −kx + wt + θ 0 is the element state of the soliton. k, θ 0, w and v are the soliton frequency, phase constant, wave number and the velocity, respectively. Substituting Eqs. (3)-(6) into Eq. (1) we get the real and imaginary parts of this equation separately as,
From (7) and (8) we get,
For (2n + 1)λ + 2nµ = 0 and σ = 0 we have v = (2kα 1 − α 2 w − σu 2 /(α 2 k − 1)) and λ = −2nµ/(2n + 1)
Thus, the general form is obtained from (7) and (8) as,
For n 1 = α 1−α 2 v and n 2 = α 1 k 2−w+kv(1−α 2 k) Eq. (10) becomes
Applying the balance rule, we get (2n + 1)m = m + 2 ⇒ m = 2/2n = 1/n, n 6= 0.
In addition, by considering the transformation u = R 1/n , we obtain
Substituting this transformation in Eq. (11), we get
Again, balancing of Eq. (13) leads to m + m + 2 = 4m so we get m = 1, hence the solution according to the MSEM is,
therefore, we can write:
Moreover, substituting R(ζ) in Eq. (13) and collecting the coefficients of different power of ψ −j , equating them to zero implies this system of equations:
Firstly, from Eq. (20) and Eq. (24) we obtain:
Now, from Eq. (21) and Eq. (22) we get
By integrating Eq. (26) we get,
Also, by integrating Eq. (23) leads to
Dividing Eq. (28) by Eq. (27) implies
We can easily obtain the solution by substituting Eq. (23), Eq. (24) and Eq. (29) into Eq. (14) as follows,
Consequently,
3 The exact solutions using the RPSOM
According to the RPSOM [4] the solution is
where the parameters A,B,C and M can be calculated later. Note that when AC ≠ 0 and M = 0, Eq. (35) is a Riccati equation. When A ≠ 0, C = 0 and M ≠ 1, Eq. (34) is a Bernoulli equation. Differentiating Eq. (35) once, we get,
Substituting about the distinct derivatives of R into Eq. (35) and setting equality for the highest exponential order of R we obtained the value of M. Now, equating distinct coefficients of R i implies a set of equations in terms A,B,C and λ from which we can calculate them.
Now, using the transformation ζ = x + y − λt as well as the values of A,B,C and λ into the auxiliary Eq. (35), then it will admit these forms of solutions:
and
when M ≠ 1, A ≠ 0and B 2-4AC < 0.
and
when M ≠ 1, A ≠ 0and B 2-4AC < 0.
when M ≠ 1, A ≠ 0 and B 2 − 4AC = 0, where C 1 is an arbitrary constant. Now, according to the constructed method
Substituting into Eq. (13), we get
Equating the coefficients of different powers of R to zero we obtain,
Equating the coefficients of different powers of R to zero we obtain,
From these equations we obtain,
According to the proposed method we take the 4-th case for which M ≠ 1, A ≠ 0 and B 2−4AC < 0, the solution of Eq. (13) is
Consequently,
4. Graphical interpretation
In this section we illustrate the soliton solutions of the generalized perturbed full nonlinearity complex Fokas-Lenells equation The real part and modulus of optical soliton are depicted in 3D plot and 2D plot in each figure. In Fig. 1, the plots of soliton solutions (32) are established with the constant values α 1 = 4,α 2 = 1,b = −2,n = 3,ν = 1,k = 10,w = 2,c 1 = 3 and θ 0 = 2.
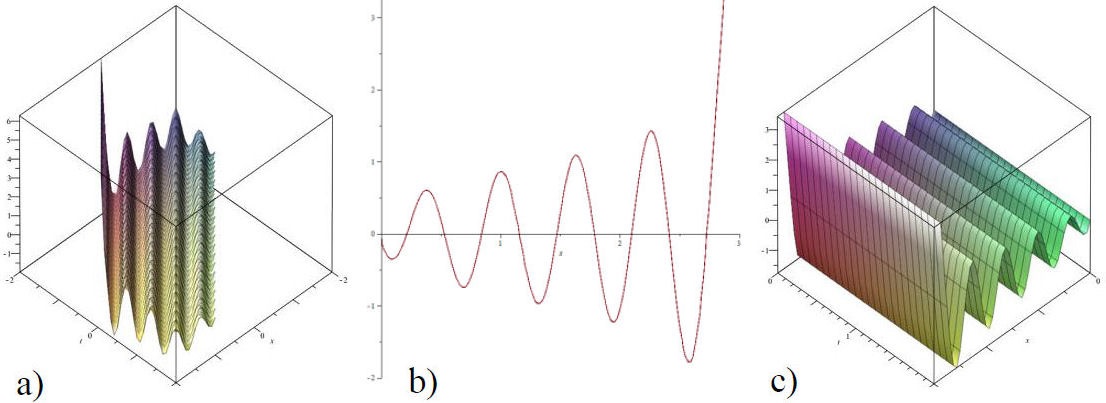
FIGURE 1 Soliton solution with α 1 =4, α 2 =1, b =−2, n =3, ν =1, k =10, w =2, c 1 =3 and θ 0 = 2. a) Three dimensional plot, b) Line chart, c) Two dimensional plot.
It is assumed that α 1 = 4, α 2 = 1, b = −2, n = 3, ν = 1, k = 10, w = 10, c 1 = 1 and θ 0 = 2 in Fig. 2, where we first illustrate the soliton solution (60) in three dimension (Fig. 2a)) and then 2D plots are depicted in Figs. 2b) and 2c).
5. Conclusion
In this work the MSEM and the RPSOM are used in the same vein and parallel as a powerful advance for future studies to get the new exact optical solutions for the generalized perturbed full nonlinearity complex Fokas-Lenells model (GPFNCFL). These solutions will brief positive accuracy to the quasi-particle theory to suppress intra-channels collision of optical solitons corresponding Langevin equations in order to obtain the mean free velocities of the soliton, and proved the phenomena of soliton cooling using the distortion terms. We also conclude that these different techniques are concise, effective, powerful, and direct. Furthermore, they reduce the large amount of calculations and can be used to any nonlinear problem of science.
