1. Introduction

The development of new magnetic nanomaterials has gained much importance due to their novel applications in several disciplines, mainly those related to biomedical applications¹.

Currently, iron oxide magnetic nanoparticles (MNPs) of magnetite are manufactured following various chemical methods^2,3, obtaining beads with spherical shape and core-shell structures, which have high magnetic saturation, low hysteresis, and good biocompatibility with cell cultures^1,4. The theoretical modeling of the MNPs allows us to study the magnetic behavior of these nanomaterials under different thermodynamic conditions, also to quantify the interaction between nanoparticles to determine the magnetic anisotropic effects involved⁵.

The ferrimagnetic behavior of magnetite and a lot of ferrites was widely explained by Louis Néel during the 20th century. In magnetite, this response is caused by the tetrahedral and octahedral overlapped sublattices of the ions Fe3+ and Fe2+/Fe3+, which are located in the interstitial places of the crystalline structure FCC formed by the oxygen atoms, where the antiparallel orientation of the magnetic moments are arranged as an “antiferromagnetic imperfect ordering⁶”. The antiferromagnetic and ferrimagnetic orderings depend on the temperature T and both disappear above a critical temperature T_N or T_C (called Néel or Curie temperature, respectively), reaching a paramagnetic behavior^6,7.

Monte Carlo (MC) computer simulations are a useful alternative to complement the analysis of the magnetic properties of the MNPs; several works have modeled the magnetization M of antiferromagnetic systems based on iron oxides (or magnetic systems in general) employing the Ising model^8-10. Other works have used MC computer simulations with similar purposes, but using an oversimplified model, which considers a fluid of magnetic hard spheres (MHS) or discs, which are influenced by a magnetic field of magnitude H^11,12.

The main aim of this work is to study both experimentally and theoretically the magnetization (M) behavior of magnetic core-shell spheres (CSS), with a particular interest in CSS of magnetite coated with dopamine. This type of nanoparticles has been probed successfully in vitro and in vivo experiments of magnetic hyperthermia. The molecular approach here considered to carry out MC computer simulations is explicitly built with the measured parameters of the CSS, such as the diameter of the magnetic core, thickness of the coating, magnetic moment, concentration of MNPs, magnetic field, anisotropy constant, and temperature. Later, the computed magnetization dependences M vs H and M vs T are analyzed and compared with those obtained using a vibrating sample magnetometer (VSM).

Thus, by combining MC computer simulations and analytical approximations for the magnetization, using some physical parameters about the composition and magnetic moment of the CSS, it is possible to reach a better understanding of their magnetic properties in a wide interval of temperatures. Our main hypothesis is that the main mechanisms of magnetization can be accounted for by considering explicitly the excluded volume interaction, the dipole-dipole interaction between the coated nanoparticles, the external magnetic field, and the anisotropic magnetic contribution.

2. Theoretical background

2.1. Potential model

To carry out the computer simulations of the magnetic CSS, we consider a simplified fluid composed of N spheres of diameter σ (magnetic hard-spheres; MHS) of volume V_i within a volume V at a temperature T. The MHS can be oriented by an external magnetic field B following the Zeeman energy law, since each sphere has an intrinsic dipolar moment μ_i. Therefore, dipole-dipole interactions between MHS should be taken into account. Additionally, the uniaxial anisotropy energy of the CSS is explicitly considered by introducing its magnetic anisotropy constant k_i and the orientation of the anisotropy along the k^i-axis, i.e., the axis of magnetization, associated with the magnetic moment μ⃗i=MSVim^i. The coordinate system and all the vectors involved are depicted in Fig. 1, where m^ and ĥ_i are unitary vectors oriented in the directions of the magnetic moment of the particles and the external magnetic field H, respectively.

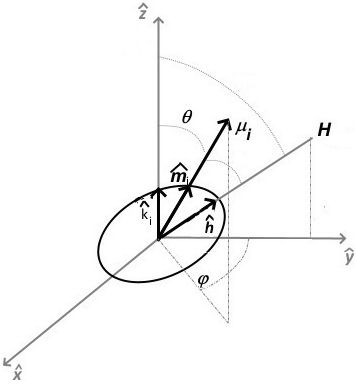
Figure 1 The coordinate system and all the vectors and angles with the origin in the geometric center of a CSS. 

The Hamiltonian of the dipolar fluid is given by,

H=K+Vhs-μ04π∑i3(μi⋅rij)(μj⋅rij)|rij|5-(μi⋅μj)|rij|3-∑iμi⋅B-∑ikVik^i⋅m^i2, (1)

where K is the kinetic energy and V_hs represents the typical hard-sphere repulsive interaction at short distances¹³.

3. Material and methods

To carry out a comparative analysis between the magnetization obtained experimentally and the one computed via MC computer simulations, the CSS are initially characterized to determine the parameters required by the MC algorithm, such as the inner and outer diameters of the CSS, the concentration, and effective magnetic moment. Then, TEM microscopy experiments, thermogravimetric measurements, and magnetometry are performed. The MNPs were prepared by chemical coprecipitation and the procedure is widely described in a previous experimental report²⁰. The CSS obtained are MNPs with a core of magnetite, which are coated with dopamine by ultrasonication. Particle shape and size are analyzed using a TEM JEOL JEM-2100 with FCF-200-Cu grids, where an aliquot dilution 1:100 concentrated at 0.01 mg/ml is dried at room temperature inside of a vacuum chamber. The amount of dopamine covering the core is estimated using a thermogravimetric analyzer TGA Q500 (TA Instruments). Experiments are carried out inside of inert N atmosphere with a flux of 25 ml/min, establishing a heating rate of 10°C/min and covering the interval 40 < T < 850°C.

To estimate the magnetic moment μCS of an individual CSS, m_d = 1.4 mg of dried mass is analyzed by a VSM (VersaLab of Quantum Design). The sample is initially heated at 400 K for 10 min and after that, it is magnetized at room temperature with H = 2387 kA/m to determine the total magnetic moment when the sample is magnetically saturated. Additionally, the magnetization of the sample is registered at T = 300 K over the magnetic field amplitude interval -2387 < H < 2387 kA/m. To determine κ, the magnetization traces ZFC and FC are measured over the temperature interval 50 < T < 400 K, using the constant intensity H = 7.96 kA/m.

4. Results and discussion

In Fig. 2a), a typical TEM micrograph is shown, where a spherical shape of the CSS is evident. After an analysis of a set of micrographs using the ImageJ software (https://imagej.nih.gov/ij/), the relative frequencies of the diameters are computed and displayed in Fig. 2b), leading to a mean particle diameter of σ_c = 13(5 nm. Nevertheless, this diameter does not include the thickness of the coating because dopamine was partially o completely evaporated during the TEM measurements. However, the mass of dopamine covering the core is evaporated under controlled conditions during the TGA assay, and Fig. 2c) shows the relative dependence of mass loss on temperature. When the sample is heated up to 800, the shell of dopamine is completely evaporated, reaching a total relative amount of 13%. According to Eq. (14), the mass fractions estimated are η_c = 0.87 and η_s = 0.13. Then, using the measured σ_c plus the known densities ρ_c = 5.18 g/cm³ and ρ_s = 1.26 g/cm³, the width of the coating computed with Eq. (16) is Δ = 1.1 nm. Thus, the diameter of a CSS is approximately σ_cs = σ_C + 2Δ ≈ 15 ± 5 nm.

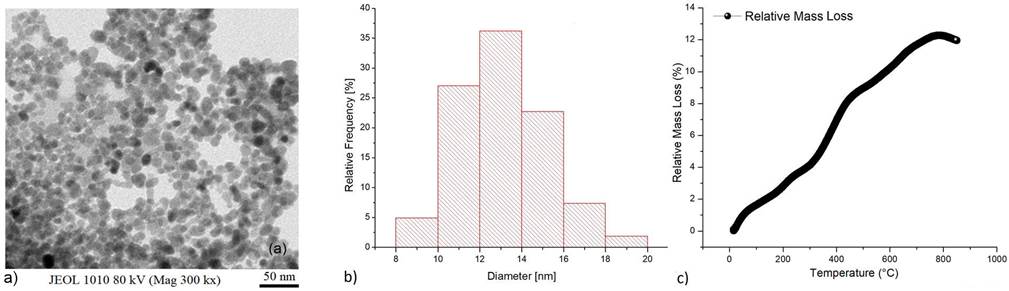
Figure 2 a) A typical TEM micrograph of the MNPs, b) the bars plot of the particle diameter distribution, and c) the mass loss dependence with temperature. 

According to VSM measurements, the total magnetic moment reached of m_d is μ_T = 0.035 emu (at room temperature and using H = 2387 kA/m). The resulting magnetic moment per CSS μ_CS = 1.63 x 10^-19 Am² (MKS units) was determined by computing the amount of CSS (N_CS = 2.1 ( 10¹⁴) using the effective mass m_cs = ρ_cs * V_CS = 6.67 x 10^-18 g and the ratio N_cs = m_d/m_cs. In the subsequent VSM experiments, the FZF-FC protocol was followed to determine M with H = 7.96 kA/m, and the dependence of the magnetization with temperature is plotted in Fig. 3a). In the ZFC trace, the slow growth of M highlights the size polydispersity of the CSS, which is according to the standard deviation of the bars plot displayed in Fig. 2b). The high magnetization observed at 50 K can be associated with a remanent magnetization of the sample because the maximum warming (400 K) was not sufficient to produce a random distribution of the magnetic moments, but the temperature cannot be increased to avoid the evaporation of the organic shell (see Fig. 2c). Furthermore, the monotonous decreasing of the FC trace below 225 K indicated the importance of the dipolar interactions, which are the main driving force behind the reordering of the magnetic moments in antiparallel orientations to diminish the total magnetization²¹. A careful observation of the maximum M reached in the ZFC trace allows us to get the blocking temperature Tb = 276 K. Another alternative to determine Tb is by analyzing the derivative of MZFC - MFC and fitting it using a log-normal regression procedure, as shown in Fig. 3(b), which also allowed us to get the following value Tb = 102 K. According to²², Tb = 276 K would be a good representation of the blocking temperature only for a monodisperse ensemble of MNPs, whereas Tb = 102 K is a more accurate approximation to the effective blocking temperature for a polydisperse system, like the one depicted by Fig. 2(b). The Néel-Arrhenius law for the magnetic relaxation time Τ_N of superparamagnetic materials is given by Τ_N = (0e^κVC/kBTb, where T₀ = 1.0 ns is the constant of the time scale. Then, T_N coincides with the sampling time of the VSM (t = 100). Two possible values for the anisotropy constant κ may be associated with the core of the CSS, namely, κ₁₀₂ = 30.6 kJ/m³ and κ₂₇₆ = 82.8 kJ/m³. Although the ZFC-FC protocol is a useful alternative to determine κ, it is important to highlight that both traces exhibit a nonequilibrium magnetization, because it depends on the magnetic history of the material.

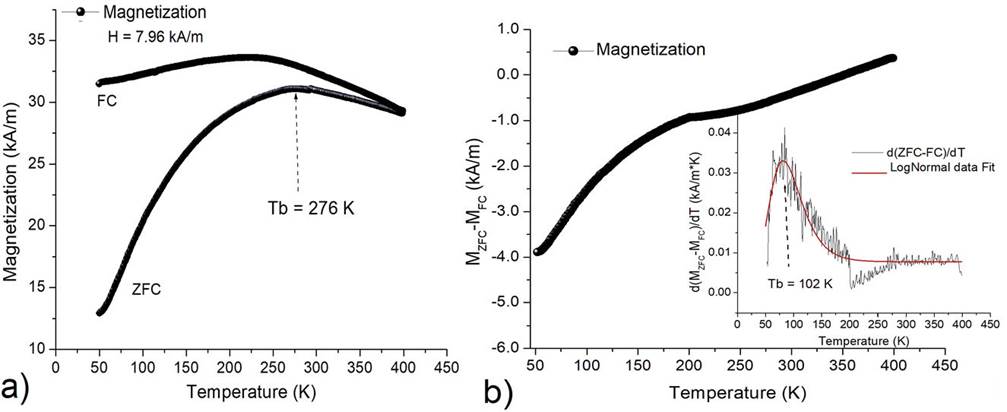
Figure 3 a) The dependence M vs T following the ZFC-FC protocol using H = 7.96 kA/m; b) the dependence (M_ZFC - M_FC) vs T with the derivative in the inset, plus its corresponding LogNormal fit. 

Then, the following experimental parameters are explicitly used in Eq. (1) to carry out the MC computer simulations: μ = μ_CS, T = 300 K, V_i = V_CS, κ = 0; κ₁₀₂; κ₂₇₆, and the interval -2387 < H < 2387 kA/m. At the beginning of the simulation, the anisotropy axis of each particle k^i is randomly oriented. In Fig. 4(a), three magnetization curves are plotted, which were computed considering each value of κ. Additionally, the experimental one obtained using the VSM is also displayed. For high magnetic fields, all curves appear to be collapsed. In fact, the difference between the experimental magnetic saturation (90 kA/m) and the obtained via MC is up to 1%, showing independence of κ. As can be observed in the inset of Fig. 4(a), for lower magnetic fields things change because the slopes of the curves (initial magnetic susceptibilities) increase when κ diminishes. According to this observation, the magnetization is again computed, but now using κ = κ₁₀₂ with two different orientations of the anisotropy axis k^i, the same direction of m^i and ĥ_i, separately. Figure 4b) shows five magnetization curves, one for each orientation of k^i, also including the random orientation of k^i, κ = 0, and the experimental one. As can be seen, all curves are intercepted only in the higher magnetic field and the magnetic saturation has the same value as discussed in Fig. 2a). In the same sense, the parameter Χ (see inset of Fig. 4b) corresponding to k^i, oriented in the same direction of μ_CS and H, is even less than the obtained when k^i is randomly oriented. This dependence k^i vs Χ was previously reported in Ref.³.

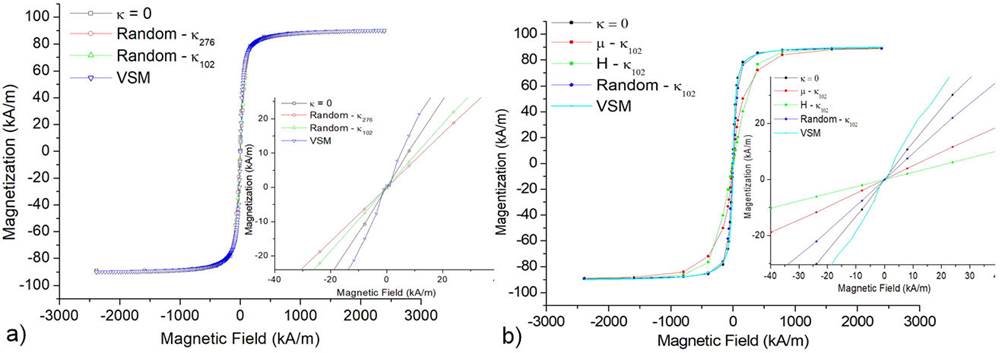
Figure 4 Dependences M vs H considering: a) κ = 0, κ₁₀₂ and κ₂₇₆; with randomly oriented, plus the experimental plot obtained via VSM; b) κ = 0, κ ₁₀₂; with oriented in the directions m^i, ĥ_i, and random, plus the experimental plot. The slopes of the lines in the insets represent the magnetic susceptibilities. 

The dependence of the magnetization on the temperature is discussed now. The temperature interval in the VSM experiment was 50 < T < K, whereas in the MC simulation, it is not limited. In Fig. 5a), the curves for weak magnetic intensities, namely, H = 0, 0.796, 3.18 (with κ = 0, κ = κ₁₀₂) and 7.96 kA/m are shown. As the acceptance rate of the MC simulation is drastically decreased below 20 K, we have restricted the analysis to the interval 20 < T < 400 K. In all curves, the magnetizations reached maximum values between 30 K and 40 K and suffers a significant decrease at 20 K. Above 100 K, all curves (except H = 0 kA/m) satisfy the Curie law, as can be observed in the corresponding plots 1/Χ vs T of Fig. 5b); all points almost collapse in a straight line. When κ = 0, it is found the lower slope (< 45%) because the magnetic susceptibility Χ has reached the highest value, showing a good agreement with the magnetization curve of Figs. 4a) and b). When the amplitude of H is very weak, the main contribution to the energy of the MHS is provided by the dipolar interactions Udd and the anisotropy energy Uanis. Further analysis of the rate Udd/Uanis exhibits Udd/Uanis ≈ 2/3 above 100 K and below Udd/Uanis ≈ 3/2. This last behavior agrees with the observations of the dipolar interactions in the FC trace of the magnetization obtained in Ref.²¹.

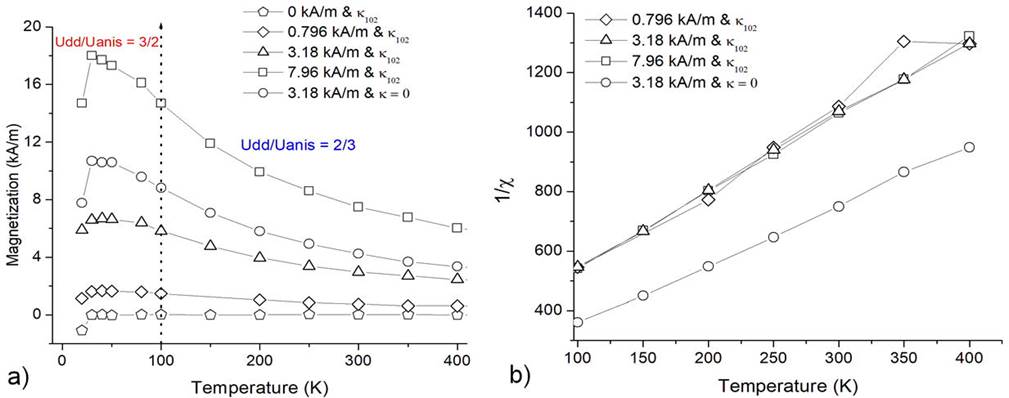
Figure 5 a) The dependences M vs T obtained via MC with different magnetic field intensities, κ = κ102, and κ = 0 plotted in the interval 20 < T < 400 K. b) The dependence 1/Χ vs T in the interval 100 < T < 400 K. 

To highlight the importance of the dipolar interactions at low temperatures, in Fig. 6 configurations of the MHS (magnetized with H = 7.96 kA/m) are shown for two different temperatures, namely, 100 K and 20 K. The spheres are placed in the corresponding spatial positions and the arrows describe the orientation of the magnetic moments. As can be observed in the XYZ view and the XY projection, the orientations at 100 K have some random distribution. The opposite behavior is observed at 20 K, where the magnetic moments are aligned perpendicularly to z^, arranging planes antiparallel oriented like an “antiferromagnetic or ferrimagnetic domain”.

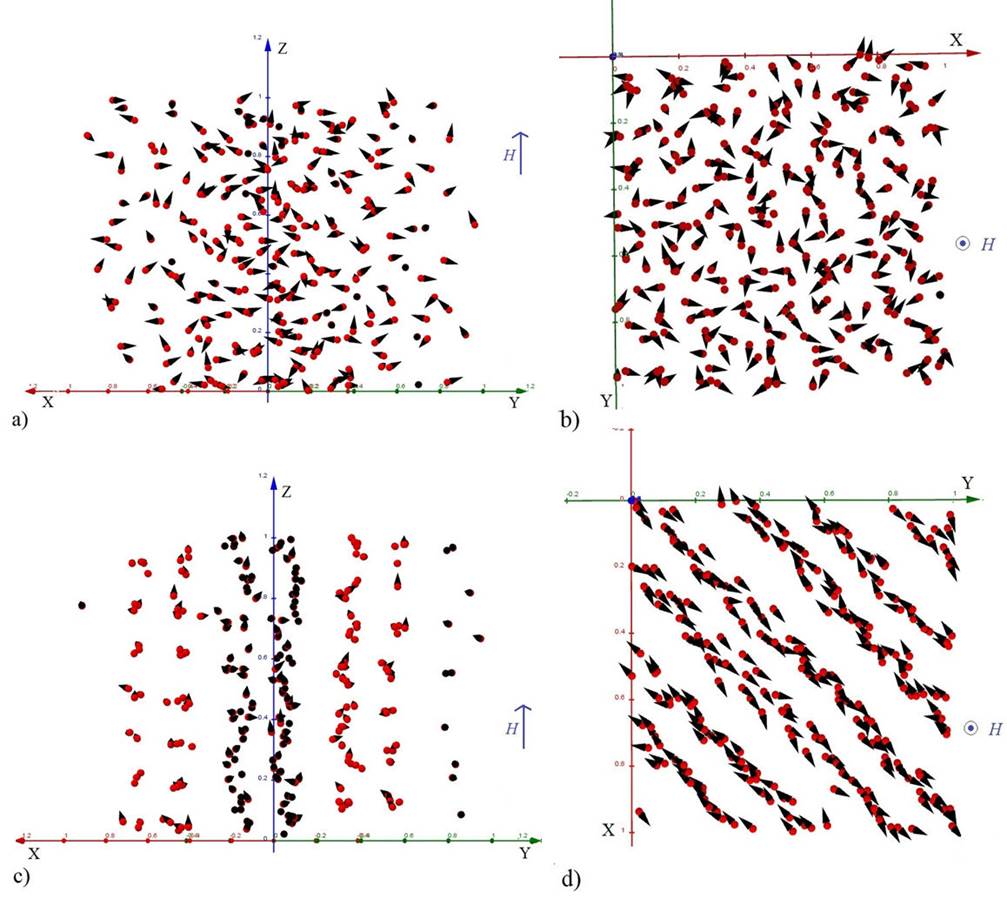
Figure 6 Thermalized configurations of the MHS inside of the simulation box in isometric views XYZ and the respective XY projections applying H = 7.96 kA/m z^: at a), b) 100 K and at c), d) 20 K. 

A discussion about the theoretical models for M applied to the experimental (M_VSM) and the simulated curve (M_κ102) when k^i is randomly oriented is conducted now. For this purpose, M_VSM and M_κ102 are plotted with the corresponding Langevin magnetization (see Eq. (3)). Also, the magnetization approximated for low (M_L) and high (M_H) fields with Eqs. (10) and (11), respectively, are included. Starting with M_VSM, Fig. 7 shows a full-scale view of this qualitative comparison. As can be expected for a sample mainly superparamagnetic, the difference between the M_VSM and the Langevin equation is only perceptible in the inflection range of H, that is, where the linear response fails and the sample became saturated. However, the inset (I) in Fig. 7 shows a close-up in the high field region (H > 2κ/(₀M_S), where M_H predicts more accurately the real magnetization M_VSM. Inset (II) in Fig. 7 also shows a close-up with M_L, where M_VSM has a greater slope than even the Langevin equation. This suggests the existence of an interval where the dipolar interactions could be of significance, or probably a little fraction of CSS has the anisotropy axis aligned to H rather than randomly distributed.

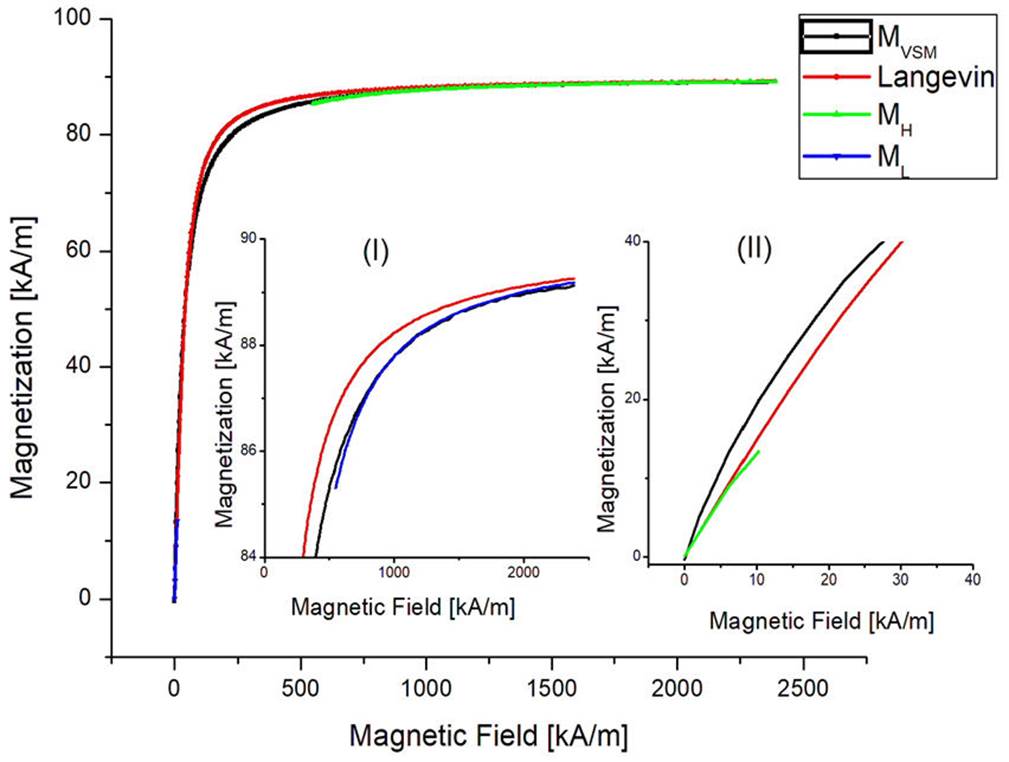
Figure 7 Magnetization M_VSM superimposed with the corresponding Langevin equation (Eq. (3)), including M_H (inset I) and M_L (inset II). 

Figure 8 shows the same qualitative analysis on M _κ102 as in Fig. 7. In the full scale of H, the Langevin model again differs only near the transition to magnetic saturation. Nevertheless, inset (I) of Fig. 8 shows M_H with a better agreement with M_VSM. Moreover, in the inset (II) of Fig. 8, M_L remains under the Langevin limit, even when the simulation has taken into account the dipolar interactions. This reinforces the idea that the initial slop of the experimental curve provided in the inset of Fig. 7 must be due to the presence of a fraction of particles where the anisotropy axis is aligned with the external field.

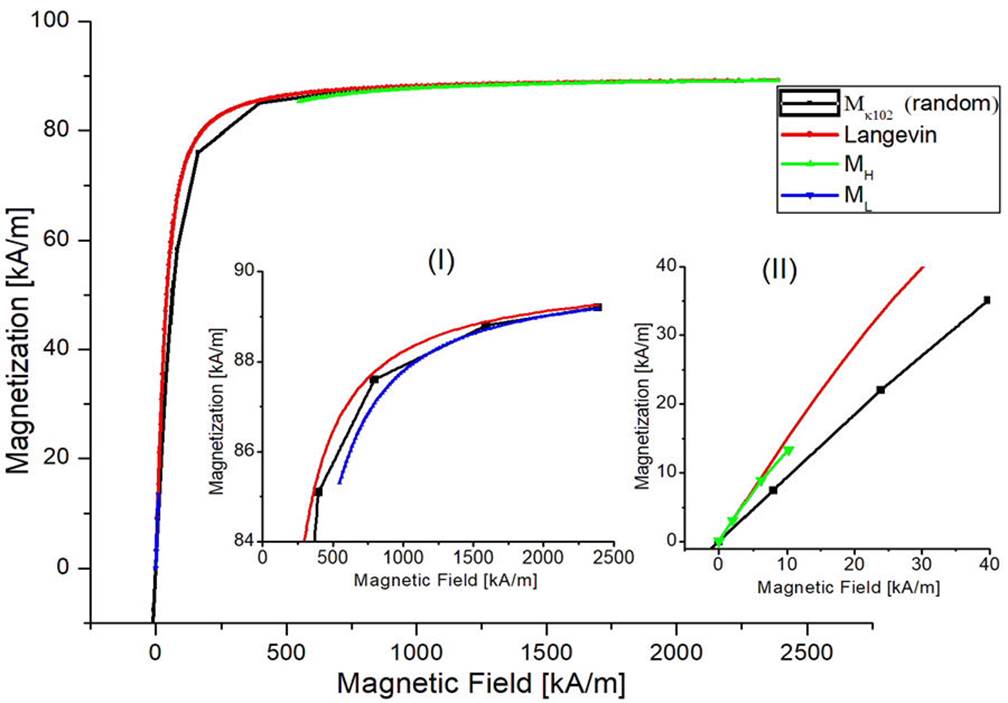
Figure 8 Magnetization M_κ102 superimposed with the corresponding Langevin equation (Eq. (3)), including MH (inset I) and ML (inset II). 

5. Conclusions

A detailed characterization of a magnetite-dopamine core-shell nanoparticle sample was presented, including direct measurement of particle size through TEM microscopy, the thickness of coating using TGA, the blocking temperature and M vs H response, by vibrating sample magnetometry. Using those measurements, the parameters needed to carry out MC computer simulations were obtained. The dependence of H on the magnetization was studied by Monte Carlo computer simulations, using two possible magnetic anisotropy constants and three different orientations of the anisotropy axis k^i. As was observed, when the CSS have κ₁₀₂ = 30.6 kJ/m³ with k^i randomly oriented, the simulation predicted an M vs H dependence more similar to the experimentally measured and fitted to an ideal Langevin equation. Additionally, it was demonstrated that the correlation of the magnetization with H can be improved (in the limits of high and weak amplitudes of H) when the anisotropy contributions are explicitly taken into account. Furthermore, the dependence of T on the magnetization estimated by MC exhibited the non-compliance of the Curie law below T = 100 K, which almost coincides with the minimum Tb = 102 K measured. At these temperatures, the dipolar interactions mainly contributed to the total energy of the ensemble and the CSS adopted an ordered orientation even when the magnetic field was null.

Last, but not least, we should point out that this work also provided a condensed derivation of the magnetization including different physical contributions, which might be implemented in further works to properly analyze the magnetization beyond the ideal Langevin equation.