1. Introduction
During the last two decades, due to their possible applications in spintronics/magnetoelectronics, for half-metallic ferromagnetic compounds with unique electronic structures, one of the two spin channels is semiconducting and the other is metallic. As promising spintronic candidates, they exhibit a complete spin polarization of carriers near the Fermi level (EF) [1, 2] Heusler alloys are named for the German mining engineer and chemist Friedrich Heusler, who investigated Cu-Mn-Al alloys around the year 1900. Heusler compounds are ternary intermetallic compounds, which have been known since 1903 [3].
Heusler alloys are represented by two variants: the half-Heusler XYZ compounds and the full-Heusler X2YZ alloys. The stoichiometric composition of the Full-Heusler is X2YZ, where X and Y represent two different transition metals (or a rare earth metal (RE)), and Z represents a p element of the 3rd, 4th, or 5th main group. Full-Heusler compounds are found in either Cu2AlMn-type or Hg2CuTi-type, as shown in Fig. 1.
Computer simulation is the process of mathematical modelling, performed on a computer, which is designed to predict the behaviour of or the outcome of a real-world or physical system. Since they allow to check the reliability of chosen mathematical models, computer simulations have become a useful tool for the mathematical modeling of many natural systems in physics (computational physics), astrophysics, climatology, chemistry, biology and manufacturing [4-8].
Although the family of Heusler phases contains a huge number of representatives, there is still a wide potential for inventive materials with principally interesting properties. Up to now, most Heusler alloys have been synthesized experimentally or predicted theoretically by means of density functional calculations contain transition metals 3d, however, there are few reports on the new type of Heusler compounds with rare earth elements [9-15].
To date, there are no experimentally and theoretically investigations on the Heusler alloys containing chlorine Cl or fluorine F Motivated by this, we have employed first-principles calculations founded on density functional theory and quasi-harmonic Debye model in which the phononic effects are contemplated to explore the high-pressure and high-temperature physical properties of the new Heusler alloys: Pd2PrCl and Pd2PrF with Hg2CuTi-type structure, appropriate consideration is assigned to the predictions of the structural, elastic, magnetic, electronic properties and the pressure-volume-temperature relationship, bulk modulus, heat capacity, Debye temperature, and Entropy of the Pd2PrX for the first time and we found they are HM materials and useable in spintronics processes.
2. Method of calculations
The first principles calculations were performed by employing FP-LAPW approach [16], based on the DFT [17] as implemented in WIEN2K code [18]. The Kohn Sham equations are solved self consistently using FP-LAPW method, and quasi-harmonic Debye model in which the phononic effects are considered based on GIBBS code [19] have been used to investigate thermodynamic properties of full-Heusler alloy Pd2PrX in the pressure and temperature ranges of 0-20 GPa and 0-1000 K, respectively. Employing this model, recently a several of thermodynamic properties of a vast number of Heusler alloys, like as Ni2ScAl, Ni2TiAl, Ni2Val, Co2CrGe, Mn2RuGe, Co2VAl, Co2VGa, Fe2ScP, Fe2ScAs, Hf2VAl etc., have been performancefully predicted [20-25].
Exchange and correlation effects are treated with a generalized gradient approximation (GGA) given by Perdew et al. [26], the Pr 4f electrons are treated using a GGA+U (U=1.08eV) method for the exchange-correlation effect [27].
In the calculations reported here, we use a parameter
The valence wave functions inside the spheres are expanded up to
3. Results and discussion
3.1. Structural properties
The full Heusler compounds crystallize in an ordered cubic structure with four interpenetrating face-centered-cubic (FCC) sublattices, which can be defined by four Wyckoff coordinates: A(0,0,0), B(0.25,0.25,0.25), C(0.5,0.5,0.5) and D(0.75,0.75,0.75). Two types of structure with different atomic ordering are present: the Cu2MnAl structure (Fm3m space group, No. 225), also called L21- type, in which two X atoms occupy the A and B sites while the Y atom enters into the C site, or the Hg2CuTi structure (F43m space group, No. 216), also called as XA-type, in which two X atoms occupy the A and C sites while the Y atom enters into the B site. The main group Z atom is always located at the D site for both types. According to the site preference rule in Heusler alloys, the two X atoms with more valence electrons occupy A and C positions and form the L21-type structure, and the two X atoms with less valence electron occupy A and B positions and form the XA-type structure. The two crystal structures of Pd2PrX(X=Cl, F) are shown in Fig. 1. For L21-type structure of our compounds, the four Wyckoff sites A, B, C and D are occupied by Pd(A), Pr, Pd(C) and X(Cl, F) atoms, respectively. On the other hand, for the XA-type structure, the four Wyckoff sites A, B, C and D are occupied by Pd(A), Pd(B), Pr and X(Cl, F) atoms, respectively.
In order to find the equilibrium bulk structure of Pd2PrX (X=Cl and F) compounds, the total energy with respect to the unit cell volume is minimized and fitted to the empirical Murnaghan equation of state [29]. The Energy-Volume curves for the two compounds in the ferromagnetic (FM), anti-ferromagnetic (AFM) and non-magnetic (NM) states for Cu2MnAl and Hg2CuTi-type structures were plotted in Fig. 2. Accordingly, in the two compounds, the Hg2CuTi -type structure in FM state is more stable than other structure and is introduced as the ground state structure. The equilibrium structural parameters including lattice parameter (a), bulk modulus (B), derivative of bulk modulus (B’), the cohesive energy
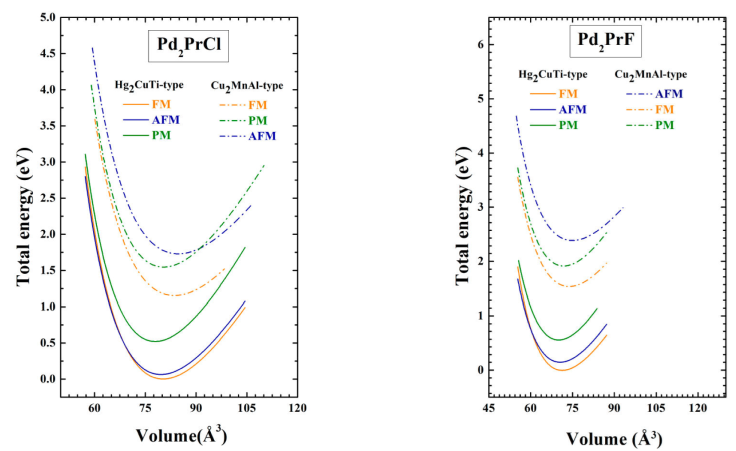
Figure 2 Total energies as functions of volume per formula unit are compared for the ferromagnetic (FM), anti-ferromagnetic (AFM) and non-magnetic (NM) states of Pd2PrX (X=Cl, F) in the Cu2MnAl and Hg2CuTi-type structures, using the GGA-PBE approximation.
Table I The calculated equilibrium lattice parameter (a), bulk modulus (B), derivative of bulk modulus (B’), the cohesive energy E
c
(eV), formation energy E
f
(eV) and the energy difference
| Compound | structure | Methods | a(Å) | B(GPa) | B’ | E c (Ry) | E f (Ry) | ΔE(mEv) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Pd2PrCl | Hg2CuTi | Our work | GGA-PBE | FM | 6.82 | 74.23 | 4.94 | -1.15 | -0.32 | 82.49 |
| NM | 6.76 | 83.24 | 4.96 | -1.11 | -0.29 | |||||
| AFM | 5.40 | 72.99 | 5.13 | -1.15 | -0.32 | |||||
| GGA+U | FM | 6.85 | 71.57 | 4.95 | -1.10 | -0.29 | ||||
| Cu2MnAl | Our work | GGA-PBE | FM | 6.92 | 65.49 | 4.74 | -1.06 | -0.24 | ||
| NM | 6.83 | 78.77 | 5.08 | -1.04 | -0.22 | |||||
| AFM | 5.51 | 60.96 | 5.15 | -1.02 | -0.20 | |||||
| Pd2PrF | Hg2CuTi | Our work | GGA-PBE | FM | 6.57 | 93.69 | 5.40 | -1.27 | -0.50 | |
| NM | 6.53 | 101.13 | 5.22 | -1.23 | -0.46 | |||||
| AFM | 5.20 | 90.17 | 5.14 | -1.26 | -0.49 | 169.33 | ||||
| GGA+U | FM | 6.58 | 90.94 | 5.43 | -1.21 | -0.45 | ||||
| Cu2MnAl | Our work | GGA-PBE | FM | 6.64 | 78.94 | 4.41 | -1.15 | -0.39 | ||
| NM | 6.58 | 92.58 | 5.14 | -1.13 | -0.36 | |||||
| AFM | 5.30 | 71.20 | 5.13 | -1.09 | -0.33 |
The cohesive energy (E c ) is always determined as the difference between the average energy of the atoms of a solid (particularly a crystal) and that of the free atoms for Pd2PrX (X=Cl, F), the E c is calculated as:
where
The negative values of E c for Pd2PrX (X=Cl, F) compounds show that our compounds are expected to be more stable with Cu2MnAl structure in FM state. So, they are possible to be synthesized in the experiment.
There is no experimental or theoretical data to compare the obtained results.
where
3.2. Elastic properties
Elastic properties of a solid are very essential seeing that they report to diverse principal solid-state characteristics such as equation of state, phonon spectra and interatomic potentials. Elastic properties are also related thermodynamically to the specific heat, thermal expansion, Debye temperature, Gruneisen parameter and melting point. So, it is necessary to determine elastic constants of solids.
Since the structure of our compounds is cubic, which need only three elastic constants in the tensor
Table II The calculated values of the three elastic constants C 11, C 12, C 44 (GPa), Kleinman parameter ζ the Cauchy pressure C p (GPa), the anisotropy factor A, Poisson’s ratio v, Lamé constants λ and μ, Young’s modulus E (GPa), the Voigt shear modulus G v (GPa), the Reuss shear modulus G R (GPa), the shear modulus G H (GPa) and Pugh’s ratio B/G for Pd2PrX (X=Cl ,F) by the GGA-PBE and GGA-PBE+U.
| Pd2PrCl | Pd2PrF | |||
|---|---|---|---|---|
| GGA | GGA+U | GGA | GGA+U | |
| C 11 | 128.92 | 133.72 | 168.15 | 132.08 |
| C 12 | 46.89 | 40.50 | 56.47 | 70 37 |
| C 44 | 16.31 | 20.86 | 25.12 | 28.33 |
| B | 74.23 | 71.57 | 93.69 | 90.94 |
| ζ | 0.505 | 0.45 | 0.44 | 0.65 |
| A | 0.39 | 0.44 | 0.57 | 0.91 |
| C p | 30.58 | 19.64 | 31.35 | 42.04 |
| v | 0.35 | 0.32 | 0.33 | 0.35 |
| E | 109.25 | 117.72 | 148.13 | 134.11 |
| λ | 95.59 | 79.27 | 108.10 | 115.89 |
| μ | 40.46 | 44.59 | 55.68 | 49.67 |
| G v | 26.19 | 31.16 | 37.40 | 29.34 |
| G R | 21.48 | 26.77 | 32.20 | 29.28 |
| G H | 23.83 | 28.96 | 34.8 | 29.31 |
| B/G | 3.11 | 2.47 | 2.69 | 3.10 |
The bulk modulus B and the shear modulus G are two reputed modules for measuring compressibility and stiffness of materials. The shear modulus G defines the resistance to plastic deformation and B determines the resistance to fracture. Using the relations (4) and (5) the values of these parameters are calculated.
where
The bulk module B of the compounds is listed in the Table II, we see that the values of B calculated with the elastic constants are in accordance with our results found previously. Our results indicate that Pd2PrCl and Pd2PrF are mechanically stable.
We have also calculated Young’s modulus E which is a quantity that measures an object or substance’s resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress-strain curve in the elastic deformation region. A stiffer material will have a higher elastic modulus [33]. The Eq. (8) [34, 35] determines E according to G and B.
The value of the Young’s modulus E is greater for Pd2PrF as shown in Table II, so we can say that Pd2PrF is the stiffer.
The Kleinman parameter ζ It describes the relative positions of cation and anion sub lattices under volume conserving strain distortions for which positions are not fixed by symmetry [36] and can be expressed as:
It is current that the result of minimization of bond bending and bond stretching, respectively are ζ = 0 and ζ = 1. It is known that if the value of Kleinman parameter ζ is close to 0 the bond bending is dominated and when it closes to 1 the bond stretching is dominated. The calculated values of Kleinman parameter for our compounds are listed in Table II and the values are close to 1, thus in Pd2PrCl and Pd2PrF studied here the bond stretching will be dominated over bond bending.
The Lamé parameters (also called the Lamé coefficients, Lamé constants or Lamé moduli) are two material-dependent measures indicated by the first coefficient (λ) and second coefficient (μ) that arise in strain-stress relationships [37], this two coefficients are always positive for most of the materials and we can calculate them by the following relations (10)
Any material is isotropic when
The degree of elastic anisotropy of a solid material is measured by the anisotropic ratio (A). theoretically, it defines how far a material is from being isotropic (if A = 1 the material is purely isotropic while it deviates from this value is called anisotropic material) and its mathematical definition is given by this following equation [39]:
As shown in Table II, we observe that the values of A are not equal to unity, indicating the fact that our compounds are anisotropic.
Another important mechanical parameter is Cauchy pressure C p , used to illustrate the bonding nature of compounds. If the pressure is positive the material is expected to be ductile, and in the case of a negative pressure it is brittle, the C p is determined by the Eq. (12) [40].
From the Table II, for our materials the value of Cp is positive, this shows that the compounds are ductile.
Pugh’s ratio B/G [41] is also the factor which attributes to describe the brittle or ductile property of compounds, if B/G > 1.75 the material is ductile, otherwise the material is brittle.
Our two materials are ductile because their B/G is larger than 1.75 which is equal to 3.11 and 2.47 for Pd2PrCl and 2.69 and 3.10 for Pd2PrF with GGA-PBE and GGA-PBE+U respectively.
The Poisson’s ratio v, It is defined as the ratio of transverse contraction strain to longitudinal extension strain in the direction of stretching force, is also another element which allows to defined the ductile/brittle character of a material, according to Frantsevich rule if the poisson’s ratio is smaller than 1/3 the material will be brittle or else the material will be ductile [42], v is determined by the following equation.
As shown in Table II, we observe that the values of v are greater than 1/3 for Pd2PrX with GGA-PBE and GGA-PBE+U, again confirming the above results.
3.3. Electronic properties
The self-consistent scalar relativistic band structures for the Pd2PrX (X=Cl ,F) along the various symmetry lines within the GGA-PBE and GGA-PBE+U scheme are given in Figs. 3 and 4, there is an overall topological resemblance for the two methods. The majority spin band is metallic, while the minority spin band shows a semiconducting gap around the Fermi level, where the values are shown in Table III.
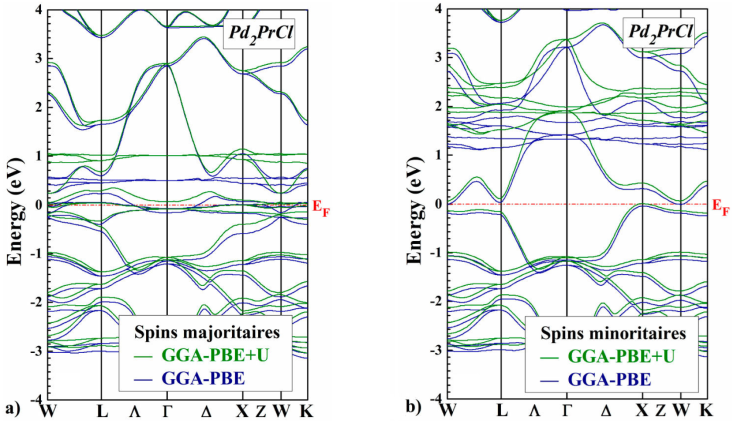
Figure 3 Comparison of GGA-PBE and GGA-PBE+U spin-polarized band structures a) spin up, and b) spin down of Pd2PrCl for the Hg2CuTi-type structure, calculated at the equilibrium lattice constant. The horizontal dashed line indicates the Fermi level.
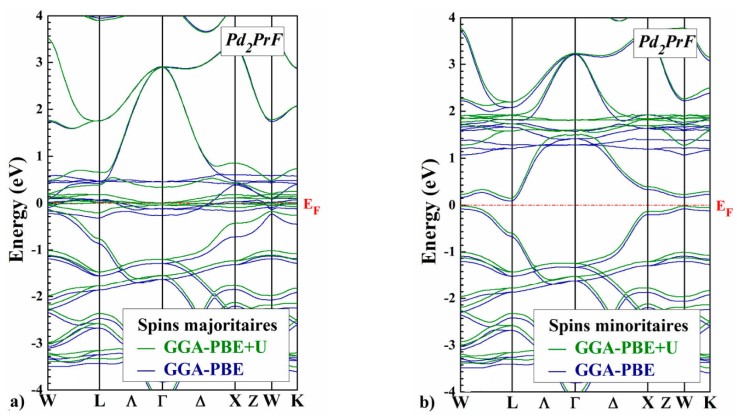
Figure 4 Comparison of GGA-PBE and GGA-PBE+U spin-polarized band structures a) spin up, and b) spin down of Pd2PrF for the Hg2CuTi-type structure, calculated at the equilibrium lattice constant. The horizontal dashed line indicates the Fermi level.
Table III Values of the energy gaps E g (eV), the total, partial and interstitial magnetic moments per formula unit of the of Pd2PrX (X=Cl,F) compounds by the GGA-PBE and GGA-PBE+U for the Hg2CuTi-type structure.
| Methods | μ inters (μB) | μ Pd1 (μB) | μ Pd2 (μB) | μ Pr (μB) | μ Cl/F (μB) | μ tot (μB) | E g (eV) | Band gap | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Pd2PrCl | Our work | GGA-PBE | 0.210 | -0.064 | -0.065 | 1.954 | -0.035 | 2.000 | 0.040 | indirect (X-L) |
| GGA-PBE+U | 0.199 | -0.088 | -0.064 | 1.989 | -0.036 | 2.000 | 0.060 | indirect (X-L) | ||
| Pd2PrF | Our work | GGA-PBE | 0.177 | -0.053 | -0.054 | 1.931 | -0.001 | 2.000 | 0.220 | indirect (W-L) |
| GGA-PBE+U | 0.215 | -0.037 | -0.064 | 1.895 | -0.009 | 2.000 | 0.250 | indirect (W-L) |
The energy gap in the minority-spin band gap leads to 100% spin polarization at the Fermi level, resulting in the half-metallic behavior at equilibrium state.
The electron spin polarization (P) at the Fermi energy (E F ) of a material is defined by the following equation:
where
The main difference which appears between the two approaches lies in the band gap of the spin-down channels of Pd2PrX (X=Cl, F). More precisely, with GGA-PBE+U approach, we can see that the band gap is more significant than the previous two. For the two approaches, we observe that the minimum of conduction band is situated at the (W) point and the maximum of valence band is located at (Γ) point and (W) for Pd2PrCl and Pd2PrF respectively, this implies that Pd2PrCl presents an indirect band gap equal to 0.06 eV and Pd2PrF presents a indirect band gap equal to 0.25 eV with the GGA-PBE+U.
3.4. Magnetic properties
The calculated values of the total, local magnetic moments and the contribution of interstitial regions for Pd2PrCl and Pd2PrF with the GGA-PBE and GGA-PBE+U methods of the Hg2CuTi-type are listed in the Table III, the magnetic moment is exactly 2 μB per unit cell.
The calculated total magnetic moment satisfies the rule of the Slater-Pauling behavior in the full-Heusler alloys [44].
In order to obtain Slater-Pauling equations for HM Pd2PrCl and Pd2PrF compounds, the band structures of these alloys should be considered.
The majority spin bands are occupied with 17 electrons. Thus, the number of occupied minority states (
where
Pd2PrCl and Pd2PrF compounds have 32 valence electrons (
3.5. Thermodynamic properties
The thermodynamic properties of Pd2PrX (X=Cl, F) are determined by using the Debye model, implemented in the GIBBS code [28, 45], It treats the vibrations of the atomic lattice (heat) as phonons in a box, in contrast to the Einstein model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low temperature dependence of the heat capacity, which is proportional to T3- the Debye T3 law [46].
From the calculated energy-volume points, the quasiharmonic Debye model allows one to obtain all the thermodynamics quantities, in which the nonequilibrium Gibbs function
which is a function of (V, P, T), where
where g(ω) is the phonon DOS (phDOS) and ω is the vibrational frequencies. Other thermodynamic properties such as entropy S, heat capacity
We employed the E - V data (total energy E and volume V) of the primitive cell as data entered into the Gibbs program. These values E and V are determined in the previous part of the structural properties in the ground state T = 0 and P = 0 as part of the approximation (PBE-GGA) using the Wien2k code. These properties are determined in the temperature range from 0 K to 1000 K for Pd2PrCl and Pd2PrF.
The interest of the thermodynamic properties in material science motivated us to investigate the cell volume, bulk modulus and the specific heats C v at constant volume and pressure.
The variation of the lattice parameter as a function of the temperature at different pressures for our compounds Pd2PrCl and Pd2PrF respectively are represented in Fig. 5.
We observe that the parameter (a) increases with increasing temperature at a given pressure, but reduced with increasing pressure at a given temperature. The growth rate of the lattice parameter with reduced temperature and with increase pressure, temperature can cause expansion and pressure can suppress this effect.
The calculated values of lattice parameter for Pd2PrCl and Pd2PrF compounds respectively at T = 300 K and P = 0 GPa are equal to 6.87 and 6.61 Å.
The Bulk Modulus is a property that defines the resistance to change of volume when compressed [47], the compressibility module variation according to the temperature at different pressures for the two compounds Pd2PrCl and Pd2PrF is represented in Fig. 6, Unlike the lattice constant, the compressibility module B 0 increases with the increase of the pressure at a given temperature, and reduced with the increase of the temperature at a given pressure.
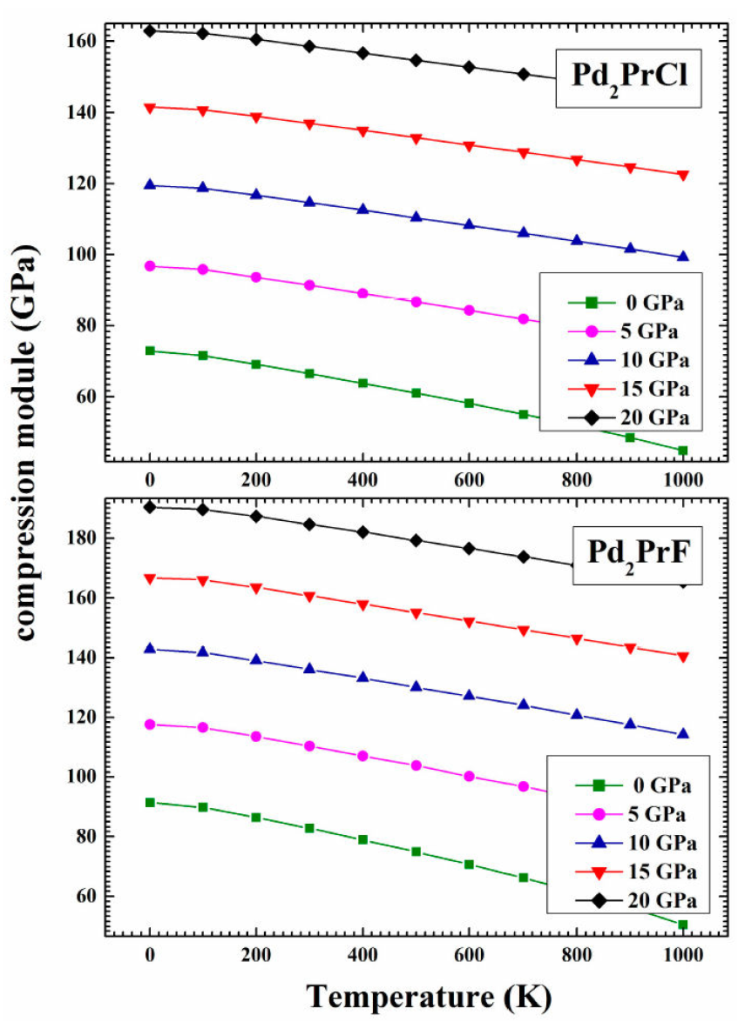
Figure 6 The compressibility module variation according to the temperature at different pressures for Pd2PrCl and Pd2PrF.
The calculated values of the compressibility module for Pd2PrCl and Pd2PrF respectively at T = 300 K and P = 0 GPa are equal to 66.07 GPa and 82.82 GPa.
The Debye temperature θ D is the temperature of a crystal’s highest normal mode of vibration, i.e., the highest temperature that can be achieved due to a single normal vibration [48]. Figure 7 show the variation of the Debye temperature θ D depending on the pressure and temperature for Pd2PrCl and Pd2PrF. We note that the debye temperature θ D decreases with the increase of the temperature at a given pressure, and increases with increasing pressure to a given temperature and we can also note that θ D is almost constant from 0 to 100 K and decreases when the temperature rises quadratically from T > 100 K, the Debye temperature values θ D for Pd2PrCl and Pd2PrF respectively at T = 300 K and P = 0 GPa are equal to 271.64 and 304.49 K.
The Heat capacity C v is an extensive property of matter, meaning that it is proportional to the size of the system. When expressing the same phenomenon as an intensive property, the heat capacity is divided by the amount of substance, mass, or volume, thus the quantity is independent of the size or extent of the sample [19].
Figure 8 represent the Variation of the heat capacity C v versus temperature at some different pressures for Pd2PrCl and Pd2PrF, at Low temperature (T < 500, T < 600. k) for Pd2PrCl and Pd2PrF respectively, the heat capacity C v is proportional to T 3.
For high temperatures C v is quite close to the classic limit of Petit and Dulong [48]. Where C v approaches approximately 99.29 and 99.30 JM-1K-1 for Pd2PrCl and Pd2PrF respectively. The calculated values of heat capacity C v at T = 300 K and P = 0 GPa are equal to 96.03 and 94.67 JM-1K-1 for Pd2PrCl and Pd2PrF respectively.
The Entropy of system S was introduced by Rudolf Clausius, he considered transfers of energy as heat and work between bodies of matter, taking temperature into account. Bodies of radiation are also covered by the same kind of reasoning [19]. The results of calculating the entropy according to the temperature at different pressures for Pd2PrCl and Pd2PrF are illustrated in Fig. 9.
We note that the entropy increases almost linearly with the increase temperature and decreases with each given pressure value. The calculated values of entropy S for Pd2PrCl and Pd2PrF respectively at T = 300 K and P = 0 GPa are equal to 146.50 and 134.81 JM-1K-1.
4. Conclusion
In this work, the full-Heusler compounds Pd2PrX (X = Cl, F) are explored. We have performed the calculations using WIEN2K package and PBE-GGA in the framework of Density Functional Theory (DFT). Elastic, mechanical, structural, electronic, magnetic and thermodynamic properties are derived and discussed.
Both the compounds are structurally stable in the ferromagnetic Hg2CuTi-type structure. The negative values of formation energies E f indicate these two alloys are easily fabricated experimentally and their formation processes are exothermic. The calculated values of cohesive energy E c confirm that Hg2CuTi structure in all compounds are more stable than Cu2MnAl structure in FM state, and are negative, the absolute values are considerable.
Elastically, we found that the required mechanical stability criteria are satisfied and consequently our compounds are ductile and anisotropic material.
Electronic properties are analyzed with the band structures by GGA-PBE and GGA-PBE+U there is an overall topological resemblance for the two methods. Both the calculations have revealed that the majority spin band is metallic, while the minority spin band shows a small band gap around the Fermi level, which indicates that our compounds are half-metallic.
The calculated total magnetic moment of 2.00 μB per formula unit is very close to integer value and agree well with the Slater- Pauling rules
Finally, we have conducted a detailed analysis of thermodynamic properties using the quasi-harmonic Debye-model implemented in the Gibbs2 code. So these full-Heusler compounds are candidate materials for future spintronic application.
Since there is no experimental or theoretical data to compare the obtained results. So our study is opened to experimental verifications because it is considered as the first theoretical predictions of the structural, elastic, mechanic, electronic, magnetic and thermodynamic properties for these compounds.











 nueva página del texto (beta)
nueva página del texto (beta)







