1 Introduction

Since the discovery of topological insulators (TIs), the concept of topology has been thoroughly established as a tool to identify electronic phases and classify quantum states of materials ^[1,2]. Initially, the procedure of classifying compounds through studying based the topology of the ground state wave function was limited to electronic phases with an energy gap, namely topological insulators, however since this scheme have been extended to include systems with gapless band structure, a new topological class has also been identified which is special class of metals, namely topological semimetals (TSMs) ^[1,3]. Since then, the landscape of predicted topological classes has increases and widened even if only through educated predictions, and not through experiments. The set of these new promising states includes^[4]; Chern insulators ^[5,6], topological insulators (TI) ^[2,7], crystalline topological insulators (CTI) ^[8], Dirac semimetals (DS)^[9,10], Weyl semimetals (WS)^[9,11], quadratic band-crossing materials^[12], topological superconductors^[13,14], new fermions and many other states^[1,3]. Until now, some new semi-metallic systems have been predicted, such as bismuth, WTe2 and NbSb2 ^[15,16,17], some heavy and light half-Heusler compounds with Dirac nodes in their bulk FS.

Heusler materials have attracted a great interest because they provide ideal candidates with extremely wide range of applications from which we are interested in spintronic applications, and also their easy synthesis which makes them great candidates for further experimental works^[18,19,20].

Furthermore, Heusler materials provide an ideal platform for deriving many new technologies by means of adjustment of the lattice parameters by substitution of isoelectronic elements or an adequate hybridization strength, in which the Heusler compounds go from trivial to non-trivial states; This flexibility positions these materials as one of the most active research fields^{[2,19,21,22,23,24]}.

Further, it should be emphasized that in addition to the fact that these materials provide an interesting new context in which to identify and understand the physical consequences of topological properties of momentum-space bands or textures in real-space, they also provide the tempting perspective to adapt the fundamental advances discovered in important new applications ^[13]. Spintronics is at the heart of our focus from these prospect applications, where mixture of the topology in quantum materials with spintronics gives rise to an emergent and growing area called topological spintronics ^{[20,25,26,27]}. This technological area focuses on the interactions accruing between the spins of the carriers within the adjacent magnets and the topological states of the material ^[20,26], thus the different spintronic effects such as spin-orbit transfer torques, spin current generation and injection, unidirectional spin-Hall effect and others, can be engineered and tuned by using different Topological materials and magnet structures^[26]. Which gives rise to an immense range of possibilities at the technological and engineering level.

In this review, through first principles calculations, and for the purpose of predicting theoretically the existence of such topological materials within the Heusler family, we have conducted an investigation on the band topological ordering of some newly designed ternary intermetallic compounds Na₂CuX (X = As, Sb, Sn and Bi). The organization of the paper is as follows. In Sec. 2, we described the employed method and the details of calculations. Results and discussions are presented in Sec. 3. Finally, conclusions and remarks are given in Sec. 4.

2 Calculation methodology

In this paper, we conducted a first-principles study on the structural and electronic properties of Na₂CuX (X = As, Sb, Sn and Bi) full Heusler compounds, through assuming the full-potential linear muffin tin orbital (FP-LMTO) method ^[28,29] based on the Density Functional Theory (DFT) ^[30,31] by performing the local-density approximation (LDA) technic ^[32,33].The calculations are carrying out once using the spin-orbit coupling (SOC) effects and again without using the SOC effects. The FP-LMTO method ^[34] used the smooth Hankel functions ^[35]. The smoothing radii and values (Hankel function decay parameters) are carefully adjusted to optimize an efficient basis set. The interstitial smooth quantities are calculating by using a fine Fourier transform mesh. To reach the energy eigenvalues convergence inside the MTSs, the charge density and potential are properly represented by spherical harmonics up to lmax= 6. The self-consistent calculations are considered to be converged when the total energy of the system is stable at 10^-6 Ry. The k integration over the Brillouin zone is performing using a tetrahedron method ^[36].

3 Results and discussion

Generally, Heusler alloys of composition 2: 1: 1 are ternaries which belong to a family of materials which crystallize in the cubic face-centered structure ^[37]. Their chemical formula is X₂YZ , where X and Y are transition metals and Z is an sp element. Moreover, Heusler alloys (Fig. 1) have generally two structures types which are; the Hg₂CuTi- type (X_Type) and the Cu₂MnAl- type (cubic L2₁).

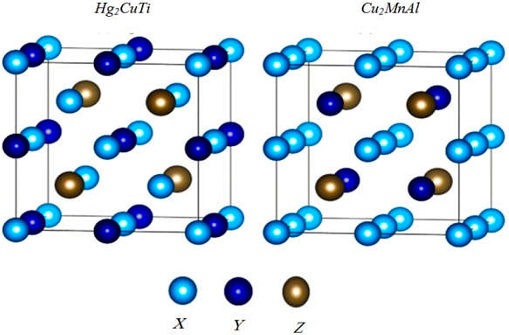
Figure 1 Crystal structures of full Heusler compound, Hg2CuTi: in which X atoms are placed in A (0,0,0) and B (1/4,1/4,1/4), Y and Z atoms are placed in C (1/2,1/2,1/2) and D (3/4,3/4,3/4) Wyckoff positions respectively, and Cu2MnAl: in which X atoms are occupied A (0,0,0) and C (1/2,1/2,1/2) sites, Y and Z atoms are occupied B (1/4,1/4,1/4) and D (3/4,3/4,3/4) sites respectively. 

Studying the properties and behavior of materials requires as starting first with the structural properties, as a first and an important step towards a better understanding of other properties. For this purpose, we have performed an optimization for our Heusler compounds in the two of structure types mentioned above. The structural properties of our Heusler compounds are calculated by performing a self-consistent calculation of the total energy in terms of cell volume. The equilibrium lattice constants (a), bulk modules (B) and its pressure derivatives (B’), are optimized by adjusting the obtained total energy in terms of cell volume (ETotal(V)) using the Birch’s equation of state ^[38]. The obtained structural proprieties are regrouped in Table I. The obtained results designate that the Hg₂CuTi- type (inverse Heusler) structure is powerfully steadier than the other structure and it is announced as the ground state structure for all the compounds. Rendering to the Table I analysis, we observed that the lattice constant has changed in terms of X element, so that; there is a direct proportionality between the atomic radius and the lattice constant. Furthermore, we can obviously understand from the Table I that the calculated bulk modules of our Heusler compounds decreases with the increasing of the atomic number. These compounds became solider when the atomic numbers decrease. It signifies bond strengthening or weakening effects induced by changing the composition ^[39].

It is necessary to check whether our materials are suitable for experimental works and possible to synthesize, therefore, we have to check their chemical stability. For this reason, we have calculated the energy of formation Ef  , which is the energy necessary to synthesize our systems from their constituent elements. The negative value of the formation energy Ef confirms the thermodynamic stability. Calculation was performed using the following equation:

where E_Tot is the energy of the Heusler compounds under their equilibrium lattice constants, and EBulkNa, EBulkCu and EBulkX are the total energies for each Na, alkali metal, Cu, and X: As, Sb, Bi and Sn atoms in their bulk states. Table I displays the calculated formation energies of our compounds. From Table I it is clear that the calculated formation energy of our compounds is negative, which means that the phases of these alloys are very compatible, and also it reflects the fact that its components are exothermic. Therefore, our alloys are promising materials in the sense that they can be easily made experimentally.

After studying and ensuring the structural and energy stability of these compounds in the previous part, we now proceed to study the electronic properties and behavior of these materials depending on the structural properties obtained above.

In order to acquire a better understanding of the electronic behavior and the topological order of the subject materials, we have analyzed the electronic structures of our compounds.

The band structures along high-symmetry directions of all compounds are calculated using LDA approach without and with SOC, and they are illustrated in Figs. 2, 3, 4 and 5.

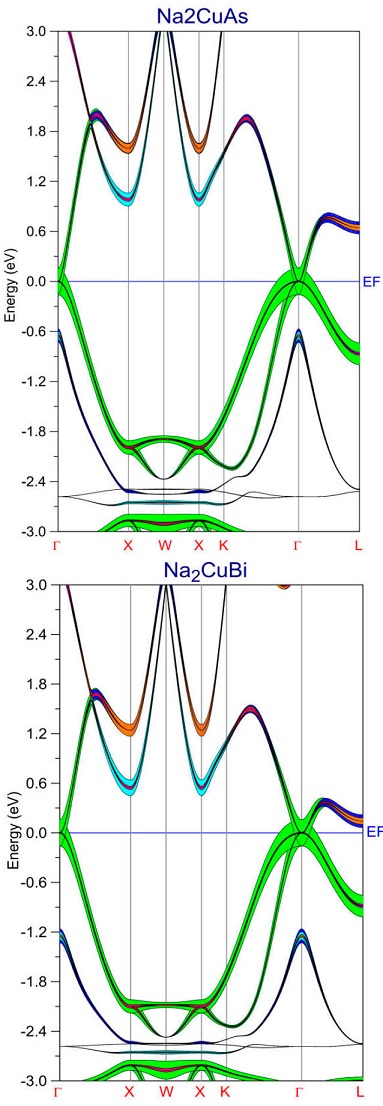
Figure 2 Band structure of Na₂CuX (X= As and Bi) full Heusler compounds using LDA approach without SOC (s-As(Bi) red; p-As(Bi) green; s-Cu blue; p-Cu purple; s-Na2 cyan; p-Na2 yellow; s-Na1 orange; p-Na1 Pink). 

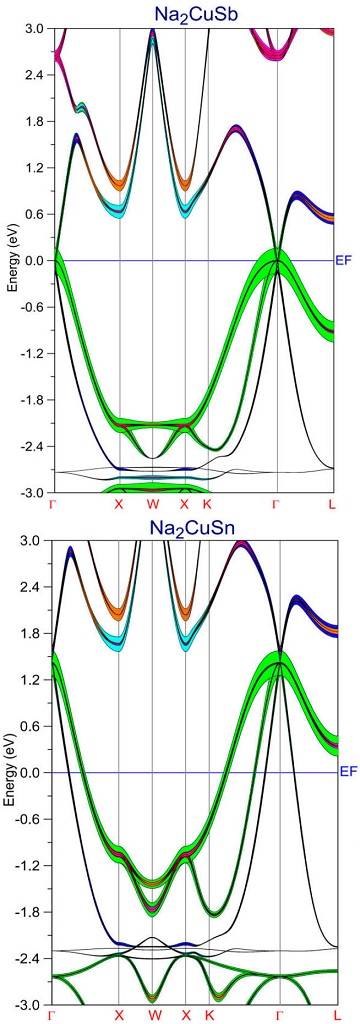
Figure 3 Band structure of Na₂CuX (X= Sb and Sn) full Heusler compounds using LDA approach without SOC (s-Sb(Sn) red; p-Sb(Sn) green; s-Cu blue; p-Cu purple; s-Na2 cyan; p-Na2 yellow; s-Na1 orange; p-Na1 Pink). 

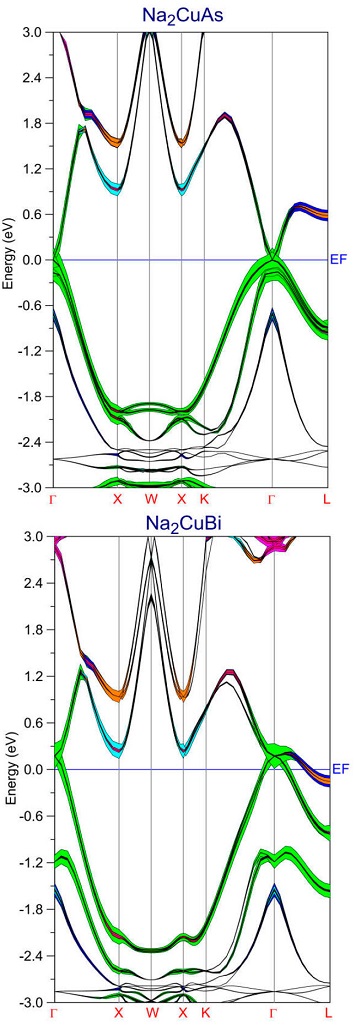
Figure 4 Band structure of Na₂CuX (X= As and Bi) full Heusler compounds using LDA approach with SOC (s-As(Bi) red; p-As(Bi) green; s-Cu blue; p-Cu purple; s-Na2 cyan; p-Na2 yellow; s-Na1 orange; p-Na1 Pink). 

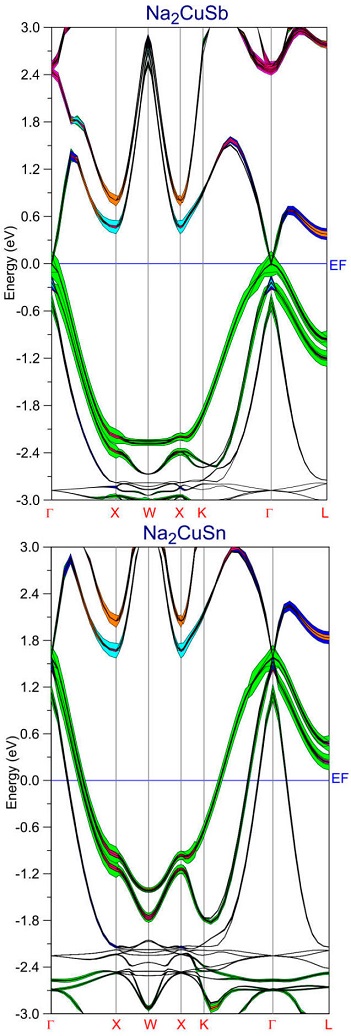
Figure 5 Band structure of Na₂CuX (X= Sb and Sn) full Heusler compounds using LDA approach with SOC (s-Sb(Sn) red; p-Sb(Sn) green; s-Cu blue; p-Cu purple; s-Na2 cyan; p-Na2 yellow; s-Na1 orange; p-Na1 Pink). 

Since the main feature indicating the topological order of the material is the ordering of electronic bands, where a band inversion at the Γ point is a strong evidence that the material has a nontrivial topological phase, thus, Fig. 2 shows that both Na₂CuAs and Na₂CuBi are topologically nontrivial compounds, this is shown clearly in the evident inversion within the band structure, where the s-like state Γ1 appears under the p-like state Γ5. In these cases, the main reason for the inversion of the band structure is due to relativistic effects ^[22,40]. In the case of Na₂CuSb and Na₂CuSn (Fig. 3), it is clear from the band structure that this compound has a trivial topology, since the single state Γ1 lies above the triple state Γ5, which corresponds to the band structure of semimetal in its natural state.

When the SOC effect is considered in the calculations (Figs. 4 and 5), the Γ5 state is divided into two states, the quadruple state Γ8 and the double states Γ7, while the Γ1 state turns into the double state Γ6. For both Na₂CuAs and Na₂CuBi, we note from the band structure that the s-like state Γ6 falls under the p-like state Γ8 and EF, which is an inverted band arrangement at Γ point; thus, these alloys have the behavior of topological non-trivial compounds in their ground state with a semi-metallic nature ^[41]. As for the band structure of Na₂CuSb and Na₂CuSn in the presence of SOC, these systems are semimetals, where the conduction and valence bands are well-separated everywhere except at Gamma.

Also, a phonon calculation is needed to assert the stability of the lattice. For this, we use the Quantum Espresso ^[42] code, and we applied density functional perturbation theory (DFPT) to estimate the dynamic strength of each structure using small atomic displacements in a 3 × 3 × 3 supercell.

The computed second-order force constants ^[43] were also used to construct the phonon spectrum. Figures 6 and 7 show the computed phonon spectra for each Na₂CuX compound along the highly symmetric points (Γ-X-W-K-L) in the first Brillouin zone. The second-order force constants in the DFPT method were used to construct the phonon spectra ^[44]. Each of the compounds has four atoms per unit cell, thus there were a total of 12 modes in each phonon spectrum. The phonon dispersion data demonstrate that Na₂CuBi, Na₂CuSb and Na₂CuSn compounds’ phonon branches are in the positive range with absent of any imaginary phonon frequencies, indicating their dynamic stability. Except the Na₂CuAs, in comparison to the other 3 compounds, we observed a negative frequency in the (Γ-X) zone, making it an unstable material.

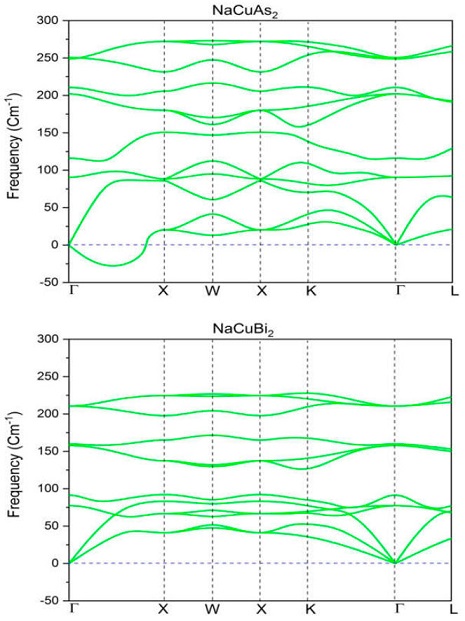
Figure 6 Computed phonon spectra of Na₂CuX (X= As and Bi) full Heusler compounds along the highly symmetric points. 

Figure 7 Computed phonon spectra of Na₂CuX (X= Sb and Sn) full Heusler compounds along the highly symmetric points. 

4 Conclusion

In this work, we have studied the potential of topological non-trivial property in the full Heusler compounds due to their promising characteristics for spintronic and quantum computing applications. In the studying of the structural proprieties, the obtained results specify that the Hg₂CuTi- type (inverse Heusler) structure is energetically more stable than the Cu₂MnAl- type structure for all compounds. Also, the negative signs of the formation energy promise the physical stability of these compounds which can continue to the fabrication step. The study of the band structures with and without SOC displays that Na₂CuAs and Na₂CuBi are all topologically nontrivial compounds due to band structure calculations screening an inverted s-p band structure. In the studying of the Na₂CuSb and Na₂CuSn electronic properties, the obtained results show that these systems are semimetals. We are encouraged that our recently predicted topological semimetals can be synthesized in the future time.