1. Introduction
Since Heusler compounds are likely to be fresh prospects for future uses, they have rekindled the attention of researchers. Intermetallic Heusler compounds are ternary ferromagnetic compounds with the general formula
Based on their estimated electronic band structures, a novel class of Heusler alloys was anticipated to be labeled “multifunctional topological insulation (TIs)”. Surface states are topologically safeguarded safeguarded against impurity fusion in this new state of matter [3, 4].
Because of their diverse properties for spintronic applications [5, 6], optoelectronics [7], superconductivity [8], shape-memory [9], giant magnetoresistance spin-valve (GMR) [10], thermoelectric applications [11], and spin injection to semiconductors [12], interest in them is steadily growing as in the thin film deposition technology [13-15].
Several theoretical and experimental attempts have been made to anticipate novel topological insulators (TIs) due to their enormous promise in spintronics and quantum computing [16, 17]. (TIs) are a relatively novel material class. Their narrative begins with Bernevig and König’s [18, 19] initial prediction of (HgTe) as a material (TI). Following this finding, (TIs) materials in binary compounds of (II-VI) group elements have been thoroughly explored.
Full-Heusler alloys are ternary intermetallic compounds with the stoichiometric composition
If the two X particles seem no longer equivalent, ternary and quaternary Full-Heusler alloys are formed. Quaternary Heusler alloys with a stoichiometric composition of (XX’YZ) commonly crystallize as the group N°216 [24-26]. The following Wyckoff coordinates
Understanding a material’s physical qualities is essential for understanding its features in terms of its operational uses [29-32]. To better understand the behavior of the
These analyses are used to calculate the phase transitions and other essential ground state features of these structures. In addition, electronic band structures are also established to comprehend the properties of the (TIs). Our calculations were carried out in the context of density functional theory (DFT) utilizing the local density approximation (LDA), employing the full-potential linear muffin-tin orbital (FPLMTO) approach as implemented in the computer code (LmtART).
To our knowledge, no theoretical or practical study on the electronic states and characteristics of these Heusler alloys has been conducted.
The following is how the remainder of the paper is organized: Section 2 contains computational details and the calculation technique, Sec. 3 has the findings of the structural, mechanical, electronic, and optical characteristics, as well as discussion, and Sec. 4 concludes with a short conclusion.
2. Computational details
Several approaches may be used to determine the physical characteristics of materials, such as electronic structures. The technique of augmented plane waves (FP-LAPW) [33, 34] and the full-potential linear muffin-tin orbital (FP-LMTO) [35, 36] are two of the most well-known ab-initio approaches that are applicable. Moreover, it may be used to solve the (DFT) equations [37], the most widely used and effective method for many years. It also has the benefit of addressing numerous atoms. The latter is now in the tens of thousands and might rise to the hundreds of thousands in the coming years. The calculations given here were performed using the Perdewe-Wang (P.W) [38] model and the (FP-LMTO) technique built inside the (DFT) as incorporated in the (LmtART MStudio MindLab 5-code) produced by S.Y Savrasov [39].
A portion of the overall energy calculations for the potential of exchange and correlation (XC) (energy/potential) was done using the local density approximation (LDA) [40]. Compared to prior versions of the (LMTO) approach, this version of (FP-LMTO) incorporates significant enhancements. The charge density/crystal potential is not subjected to any shape approximation. Furthermore, in this computational strategy, known as (FP-LMTO), the crystal unit cell is partitioned into the muffin-tin (MT) sphere region and the interstitial region (IR) for mathematical convenience, and both zones are handled on the same footing, increasing the accuracy of the eigenvalue results. Furthermore, a complete foundation is employed in this technique. For the spherical component of the potential, fundamental functions are defined in numerical solutions of the radial Schrödinger equation multiplied by spherical harmonics, while basis functions are given in terms of Fourier series for the (IR) regions. Charge density and the related potential were presented within the (MT) spheres, up to
3. Results and discussion
3.1. Phase transition and structural properties
In this part, we estimated the structural characteristics of the two full Heusler alloys
where E 0 is the ground-state total energy, V 0 is the optimal unit-cell volume, and B 0 and B’ are the bulk modulus and its pressure derivative.
Table II lists our results and additional information for the optimized lattice constants for both compounds.
Table II Equilibrium lattice constants a 0(A°) and total energy E (Ry/unit cell) for (La RuPb, Sc2 RuPb) compounds.
| Compound | Calculation | a 0(A°) | Energy E (Ry/unit cell) |
|---|---|---|---|
| 7.3760 [28] | -84911.718 | ||
| Other (Theory) | 7.3417 [29] | -84911.720 | |
| 7.3470 [30] | - | ||
| La2 RuPb | 7.1597 [LDA] X- Type | -84854.71837 | |
| Our calculation | 7.5746 [GGA] L2 - Type | -84854.7606 | |
| 7.3962 [LDA] L2 21 - Type | -84911.68004 | ||
| 7,338 [GGA] X - Type | -84911.6587 | ||
| Experimental | - | - | |
| 6.7460 [28] | -53978.04810 | ||
| Other (Theory) | 6.7531 [29] | -53978.02600 | |
| Sc2 RuPb | 6.6705 [30] | - | |
| 6.6342 [LDA] X- Type | -53939.81095 | ||
| Our calculation | 6.7263 [LDA] L2 21 - Type | -53939.82301 | |
| 6.7934 [GGA] X - Type | -53978.00554 | ||
| 6.7237 [GGA] L2 21 - Type | -53939.82461 | ||
| Experimental | - | - |
Since we are not aware of any experimental data, we compare our results with those obtained in the already-published papers of Y. Lakred and co-workers [28], A. Bahlouli and co-workers [29] for the inverse-Heusler alloys X 2RuPb, and X.M. Zhang and co-authors [30] for the Y 2RuPb investigations. Our computed values are in good correlation and agreement with those obtained by the researchers mentioned above (see Table II), which confirm the precision of our obtained results.
The theoretical values supplied in the table using the (GGA) approximation match with our estimated lattice constants for La2RuPb, Sc2RuPb. Unfortunately, to our knowledge, no experimental data for these compounds have been published.
The variation of total energy as a function of volume for the
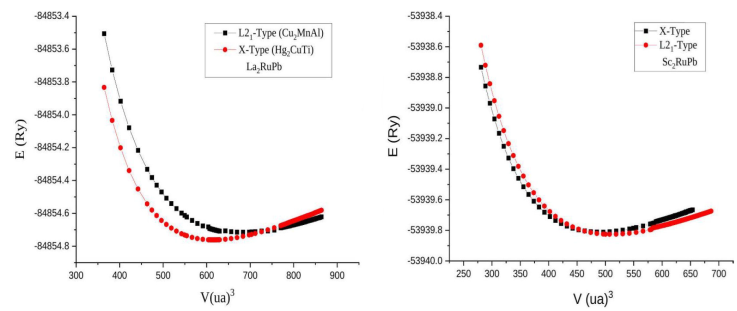
Figure 1 The variation of the total energy as a function of the volume for the compounds La2RuPb, Sc2RuPb in the Hg2CuTi, Cu2MnAl-type structures respectively.
Table III The calculated equilibrium lattice parameter a 0(A°), primitive-cell volume V 0(A°)3, bulk modulus B 0 GPa, its pressure derivative B’ and the equilibrium energy E 0 Ryd for the La2RuPb, Sc2RuPb compound in the Hg2CuTi, Cu2MnAl-type structures.
| System | structure-type | a | V 0 | B 0 | B’ | E 0 |
|---|---|---|---|---|---|---|
| La2RuPb | Hg2 CuTi | 7.1597 | 91.7538 | 93.4167 | 4.72155 | -84854.7606 |
| Sc2RuPb | Cu2MnAl | 6.7263 | 76.0796 | 127.6952 | 4.05872 | -53939.82301 |
As shown in Fig. 1, the Hg2CuTi-type structure is found to be the most stable phase for the La2RuPb compound at zero pressure because the crossing of the E(V) curve of the Hg2CuTi-phase is before the curve of the Cu2MnAl-phase for the lowest energy values, while the Sc2RuPb compound is favored in the reverse case Cu2MnAl-phase.
We believe that the values we discovered and described in the table above are consistent with those that will be found in the future by others when studying the two compounds in this or other ways, even though there was no theory or experimental values to compare them with our knowledge. The calculations of the structural properties of the two structures phases are reliable. These values encourage future experimental work to collaborate with our calculated results.
3.2. Elastic properties
The study of the mechanical properties of materials is significant for practical applications. The elastic properties of a solid are determined by the abovementioned elastic constants, which link the mechanical and dynamic behavior of a crystal and provide crucial information about the nature of the forces acting on the solid. The elastic constants, in particular, are macroscopic quantities that describe the stability, stiffness, and anisotropy of materials in inhomogeneous solids.
Understanding interatomic interactions are possible because of the influence of hydrostatic pressure. Mechanical stability and phase transition mechanisms stress to deformations allow for the evaluation of the wave’s elastic straps’ speed of propagation, as well as the assessment of mechanical properties such as ductility/brittleness, specific heat, hardness, melting point, Debye temperature, and thermal expansion coefficient [44]. Furthermore, elastic constants may be used to calculate the bulk modulus, shear modulus, Young’s modulus, and Poisson’s ratio, which are all important in calculating the strength of materials [45].
By studying the impact of hydrostatic pressure, we may learn about interatomic interactions, phase transition, and mechanical stability processes. Stresses to deformations may be used to measure mechanical qualities such as ductility/brittleness, specific heat, hardness, melting point, Debye temperature, and thermal expansion coefficient, as well as the speed of propagation of the wave’s elastic straps [44]. Furthermore, elastic constants may be used to calculate the bulk modulus, shear modulus, Young’s modulus, and Poisson’s ratio, which are all critical in calculating the strength of materials [45].
Using stress-strain equations, the second-order elastic constants (C
ij) for the La2RuPb, Sc2RuPb compounds in the
For investigation of the material hardness, the elastic properties, e.g., bulk modulus B, Voigt-Reuss-Hill shear modulus GvRH [52] and the elastic Zener anisotropy factor A [53] are given by the following formulas for cubic crystal:
Table IV shows the set of values that were obtained using the local density approximation (LDA) for the elastic constants and elastic moduli
It is worth noting that each elastic constant meets the conditions listed above in the case of the compounds of concern La2RuPb, Sc2RuPb. Bulk modulus also meets the requirement
The Poisson’s ratio plays a significant role in distinguishing between covalent and Mod ionic materials, as a small value of Poisson’s ratio of around v = 0.1 characterizes covalent materials and around v = 0.25 characterizes ionic materials [55, 56]. In this study, note that the determined Poisson’s ratio values v in both types of structures of the two compounds are more significant than the critical value 0.25 of the ionic materials, indicating that these materials are ionic.
Furthermore, we refer to Frantsevich and co-authors [55], who differentiate the ductility and brittleness of materials by the B/G ratio to comprehend the ductile and brittle nature of any compound. Frantsevich [57] further links the (ductility/brittleness) behavior to the Poisson’s ratio value v, which is smaller than 0.33 for brittle materials and more than 0.33 for ductile materials.
The calculated value of the Poisson’s ratio v, for La2RuPb is less than (0.33), classifying this compound as brittle in the
The critical value for distinguishing ductile and brittle materials is 2.76 for the B/G ratio. If the B/G ratio is greater than 2.76, the material behaves in a ductile manner. Otherwise, the material behaves in a brittle manner.
In the
However, these compounds may be categorized as ductile materials using Pugh’s criteria (B/G) ratio [58], which distinguishes ductility from brittleness for materials with a value of 1.75.
These findings are still theoretical research, which we intend to contradict shortly with experimental experiments.
We must know the value of the shear anisotropic factor A to comprehend the elastic anisotropic degree possessed by that composite. The elastic anisotropy A has a significant meaning in industrial science as it identifies micro-fractures in materials.
Where:
So, for La2RuPb, Sc2RuPb composites in the two phases’
Table IV The calculated single crystal elastic constants C ij, and the polycrystalline elastic modulus: [shear modulus G, Voigt shear modulus G v , Reuss shear modulus G r , Young’s modulus E, the Lame’s first parameter λ in GPA, Poisson’s ratio v, B/G ratio and the shear anisotropic factor A for the La2RuPb, Sc2RuPb compounds in the Hg2CuTi, Cu2MnAl-type structures.
| Parameter | La2RuPb in the Hg2CuTi-type structure | Sc2RuPb in the Cu2MnAl-type structure |
|---|---|---|
| C 11 | 117.4 | 159.3 |
| C 12 | 88.8 | 121.5 |
| C 12 | 79.8 | 93.3 |
| G | 40.888 | 49.889 |
| E | 107.732 | 133.155 |
| v | 0.3174 | 0.3345 |
| A | 5.58 | 4.9365 |
| B r | 98.333 | 134.1 |
| B v | 98.333 | 134.1 |
| G r | 28.17 | 36.238 |
| G v | 53.6 | 63.54 |
| λ | 71.074 | 100.84 |
| B/G | 2.4048 | 2.6879 |
3.3. Thermal properties (Debye temperature, Sound velocity)
The thermal characteristics dictate the best circumstances for crystal formation to begin and sustain quality. We calculate the Debye temperature θ D, an essential basic parameter for a solid’s thermodynamic characteristics, and it is linked to numerous physical properties such as specific heat, melting temperature, and elastic stiffness constants [61].
It may also distinguish between high and low-temperature areas in solids, with a greater θ D indicating higher thermal conductivity and melting temperature. It is found in equations describing properties arising from atomic vibrations and phonon theories; the determination of θ D using elastic constants at low temperatures will be the same as that of specific heat measurements, and the vibrational excitations at low temperatures are due to acoustic modes, i.e., when θ D is connected with lattice vibrations.
Because θ
D is proportional to the average sound velocity
where h is Planck’s constant, k B is Boltzmann’s constant, N A is Avogadro’s number, ρ is the density, M is the molar mass and n is the number of atoms in the unit cell.
From specific heat measurements the θ D can be calculated by the following relation [64]:
where V the molar volume in cm3/mol, M is the molar mass in g/mol, and T m the melting point in Kelvin °K.
For the polycrystalline material, the average sound velocity
where
Table V shows the calculated results of the
Table V The calculated longitudinal, transverse, and average sound velocity v l , v t , and v m , in ms-1 and the Debye temperature θ D, in °K for the La2RuPb, Sc2RuPb compounds in the Hg2CuTi, Cu2MnAl-type structures.
| Compound | Type-structure | v t | v l | v m | (θ D ) |
|---|---|---|---|---|---|
| La2RuPb | Hg2CuTi | 1503.126 | 2906.234 | 1682.709 | 209.226 |
| Sc2RuPb | Cu2MnAl | 1780.955 | 3571.375 | 1998.211 | 269.598 |
There has never been a complete investigation of the characteristics of these essential chemicals in the literature before. Consequently, our current findings may anticipate future trials and other theoretical investigations, revealing its true potential for appropriate applications under various situations.
One can clearly observe from this table that the
3.4. Electronic and optical properties
3.4.1. Electronic properties
The study of electronic properties is crucial because it allows us to investigate and comprehend the nature of the bonds between the material’s atoms.
In addition, the state density (DOS) is a necessary physical quantity for identifying a material’s physical characteristics. It may offer access to a material’s electronic and transport characteristics and an estimate of the number of binding and anti-binder states in the population with a particular energy. It also gives us access to data on electronic conductivity. Furthermore, for each atom, the electronic density is projected onto spherical harmonics of types p, d, or f, inside a sphere of a specified radius. As a result, partial state densities are produced, allowing the chemical bonding between atoms in a crystal to be determined. The total state density projections depend on the sphere radius on which the partial state densities are projected and hence only provide qualitative information.
The electronic properties of the La2RuPb, Sc2RuPb compounds in their stable phases Hg2CuTiCu2MnAl are investigated in the following section by calculating the electronic energy band structure at zero pressure along with the principal symmetry points in the Brillouin Zone, as well as the total density of states (TDOS) and the atomic site-projected I-decomposed partial densities of states (PDOS). For this, we used the (LDA) approximation to inject the theoretical mesh parameter at equilibrium previously determined in the (LmtART) code.
Figures 2a), 2b) and 3a), 3b) show the band structure and plots of the (TDOS) and (PDOS) functions calculated using the LDA of La2RuPb, Sc2RuPb compounds in both crystallographic phases Hg2CuTi, Cu2MnAl. The Fermi level enables the determination of a material’s conduction characteristics. This research aims to figure out how the electronic population varies at Fermi’s level E F .
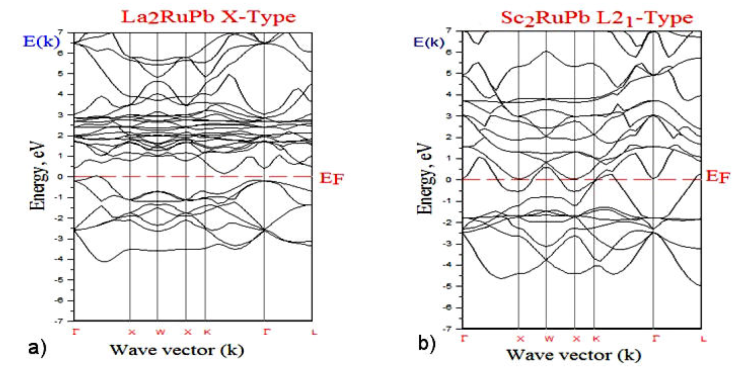
Figure 2 The bands structures along the symmetry lines of the Brillouin zone at the equilibrium lattice constant for the a) La2RuPb and b) Sc2RuPb compounds in the Hg2CuTi, Cu2MnAl-type structures.
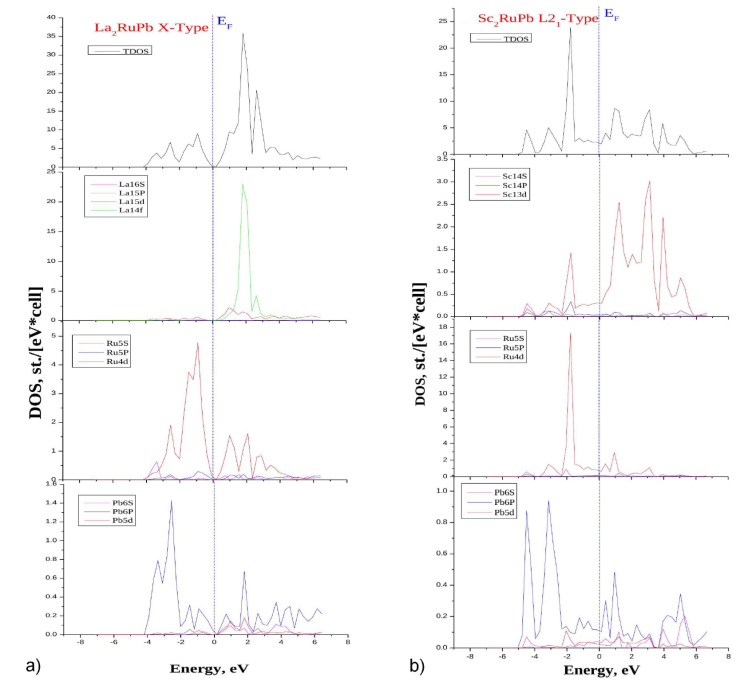
Figure 3 The total density of state (TDOS) and the partial density of state (PDOS) for the a) La2RuPb, b) Sc2RuPb compounds in the Hg2CuTi, Cu2MnAl-type structure respectively obtained by (LDA) approximation.
Although it is a recognized fact that the self-consistent (DFT) energy-gap calculations at the level of the local density approximation (LDA) exchange-correlation functional are severely underestimated, it is clear from the band structure nature of this compound, as shown in Fig. 2a), that this compound La2RuPb is a semiconductor with the direct energy bandgap within the following value 0.6044 eV at the
It is evident that in Fig. 2b), the non-existence of a gap at the Fermi level for the Sc2RuPb compound (majority) band’s structure has metallic intersections at the Fermi level confirms the assertive metallic behavior and indicates the presence of conducting features. Whereas in Fig. 2a), the La2RuPb compound (minority) band’s structure exhibits semiconductor behavior, we note an indirect energy bandgap between
We note that the band profile of the calculated band structure for the La2RuPb compound is similar to that obtained by Zhang and co-authors [28], with a slight difference due to the absence of spin-orbit in our calculation, which plays a vital role in the band inversion mechanism [34, 35, 68], and in particular, the atoms in (Y-Z) zinc-blende are much heavier than those in (X - X). We should also highlight that, as Zhang et al. [28] point out, the band topology in such compounds is very sensitive to variations in lattice constant and uniaxial strain. The La2RuPb compound combination has a positive energy difference between the
Concerning the spectrum (TDOS) of the compound Sc2RuPb shown in Fig. 3b), which is the opposite of the first compound, it can also be divided into two main sections: The first region represents the valance band, which shows the vital contribution of the 4d states of the
3.4.2. Optical properties
The various methods of light interacting with matter in solid-state physics, including absorption, transmission, reflection, and broadcast, are of significant interest. In addition, the study of solid optical characteristics is a valuable tool in our knowledge of material electronic properties. Understanding the optoelectronic behavior of a material, in particular, requires an understanding of its optical characteristics. The frequency-dependent complex permittivity of light (dielectric function) is the most significant characteristic for describing a solid’s optical properties, and the following relationship provides it [69]:
where
The integral is over the first Brillouin Zone. The momentum dipole elements:
To deduce the real part of the complex dielectric function
where P implies the principal value of the Cauchy integral. From the real and imaginary parts of the frequency dependent dielectric function, we can calculate the refractive index n(ω) following this relation [73-75]:
In this study, we used the optimized structure under equilibrium condition, which is at zero pressure, to compute the refractive index n(ω) and the frequency-dependent imaginary and real parts of the dielectric function of the La2RuPb, Sc2RuPb compounds in the (Hg2CuTi2, Cu2MnAl)-type structures, respectively. Transferring unoccupied bands from occupied bands is a typical process in the electronic energy band structure, especially near the Brillouin Zone’s high symmetry points, to explain the optical spectra. The real and imaginary parts of the dielectric function that are frequency dependent are presented in Figs. 4a) and 4b). Photons with energies between [0 and 13.6] eV are used to study the optical response of these materials.
There are multiple significant peaks in the imaginary part of the dielectric function for the two compounds La2RuPb, Sc2RuPb between 1.36-3.538 eV and 0.272-2.449 eV, respectively. These peaks illustrate how the optical transitions from the valence band to the conduction band coincide.
The spectrum also indicates the development of the first optical critical point for the dielectric function at 0.6044 eV for the material La2RuPb, as shown in Fig. 4a). The fundamental absorption edge is placed at the splitting level
For the metallic alloy Sc2RuPb, we have taken in consideration the strong contribution of the intraband transitions between VBM and CBM [76]. The obtained results show, for low energies, that there is a large difference between the curves of the real part and the imaginary part (with/without intraband), which confirms the strong contribution of the intraband transitions and confirms the strong metallic behavior of this alloy. For the highest energies, we see that the curves are almost similar, and it is obvious, because these transitions are mainly due to the transitions in the bands that overlap (VBM and CBM) close to the fermi level.
As a result, we can see that both compounds La2RuPb, Sc2RuPb have a particular anisotropic property.
We show the calculated dispersion of the refractive index n(ω)in the same spectral range in Fig. 5a) and b), which is one of the most critical factors for defining light propagation through the optical medium. Our computed static refractive index n(0)for the La2RuPb compound is 4.262 , whereas the maximum value of the predicted refractive index was 6.602 at 1.088 eV of photon energy. The static refractive index n(0)of the second compound Sc2RuPb was found to be 54.7671 for the curve with intraband transitions and 9.16597 for that without intraband. These latter high values are due to the metallic behavior of this alloy.
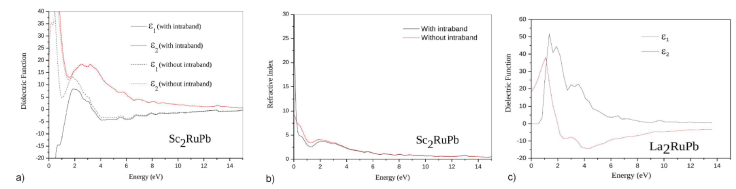
Figure 5 The real and imaginary parts of the dielectric function for the a) La2RuPb, b) Sc2RuPb compounds in the Hg2CuTi2, Cu2MnAl-type structure obtained by (LDA) approximation.
4. Conclusion
The main goal of this research was to investigate the structural (phase stability), mechanical, elastic, thermal, electronic, and optical properties of Heusler compounds
We started by looking at the structural characteristics of our X
2RuPb compounds, which showed that they are stable in the
We employed the (LDA) approach to study electronic properties, including band structure and state density. With the direct energy bandgap, our compound displays topological insulator characteristics and demonstrates that the gap at E
F
is formed by hybridization between the d-states of the transition atoms. Furthermore, the structure of the band’s findings shows metallic behavior for Sc2RuPb and semiconducting behavior for La2RuPb, with a direct gap in the
In addition to their electrical properties, the optical properties of the
We discovered satisfactory results for all of the calculated physical attributes in general. The (FP-LMTO) method’s approximation (LDA) seems to be a good fit for the Heusler investigation. Finally, to the best of the authors’ knowledge, no data on these compounds can be found in the literature.











 nueva página del texto (beta)
nueva página del texto (beta)



