1. INTRODUCTION

The majority of observed galaxies live in rather small groups containing from a few to tens of galaxies (e.g. ^{Tully 1987}, ^{Nolthenius & White 1987}, ^{Eke et al. 2004}, ^{Berlind et al. 2006}, ^{Tempel et al. 2014}). A particular subset of these systems are known as compact groups (e.g. ^{Hickson 1997}, ^{Tovmassian et al. 1999}, ^{Lee et al. 2004}, ^{de Carvalho et al. 2005}, ^{Niemi et al. 2007}, ^{McConnachie et al. 2008}, ^{Díaz-Giménez et al. 2012}), with sizes in projection (< 100kpc) a few times the optical diameters of their member galaxies and relatively well isolated from other normal galaxies and structures.

Of the best known compact groups (CGs) are those first identified by ^{Hickson (1982)}. Although some CGs in Hickson’s initial catalog are not considered any longer physical groups (e.g. ^{Sulentic 1997}, ^{Hickson 1997}), there is ample evidence, ranging from HI observations (e.g. ^{Borthakur, Yun & Verdes-Montenegro 2010}) to X-rays (e.g. Ponman et. al. 1996, ^{Desjardins et al. 2014}), and morphological signs of interactions (e.g. ^{Mendes de Oliveira & Hickson 1994}, Coziol & Plauchu-Frayn 2007), that lends support to the physical reality of many observed CGs in the sky. Observational determinations of redshifts of other compact group configurations in the sky, like the Shakhbazian-type having crossing times ∼ 0.1Gyr (^{Tovmassian & Tiersch 2008}), show that these compact structures are a definite feature of the large-scale structure of the universe.

Ever since the discovery of Hickson’s compact groups it was noticed that their dynamical time scales, many with t_d~ 0.01 t_H( tH≡H0-1), implied that they should have merged by the present epoch and led to the formation of a bright giant elliptical galaxy; further, an appreciable amount of group remnants should be detectable (e.g. ^{Carnevali, Cavaliere & Santangelo 1981}, ^{Ishizawa et al. 1983}, ^{Barnes 1985}, ^{Barnes 1989}, ^{Hickson 1997}). Different solutions to the so-called overmerging problem have been proposed in the literature, ranging from CGs being transient projections of galaxies within loose groups (e.g. ^{Mamon 1986}), projections along the line-of-sight of large-scale structure filaments (e.g. ^{Hernquist, Katz & Weinberg 1995}), the continuous ongoing formation of new compact groups either from the collapse of loose groups or through secondary infall onto an initially overdense region (e.g. Barnes 1989, ^{Diaferio et al. 1994}, ^{Governato et al. 1996}), to their galaxies being immersed in large homogeneous and virialized common dark halos, so as to increase significantly the merging time (e.g. ^{Barnes 1985}, ^{Athanassoula, Makino & Bosma 1997}, AMB97), or in a collapsing scenario out of loose groups without any initial common dark halo (^{Aceves & Velázquez 2002}).

There have been many works on the evolution of compact group-like associations of galaxies, using both dynamical (e.g. ^{Barnes 1985}, AMB97, Gómez-Flechoso & Domínguez-Tenreriro 2001, ^{Aceves & Velázquez 2002}, ^{Taranu, Dubinski & Yee 2013}) and cosmologicalmodels (e.g. ^{Diaferio et al. 1994}, ^{Governato et al. 1996}, ^{Sommer-Larsen 2006}, ^{McConnachie et al. 2008}, ^{Díaz-Giménez & Mamon 2010}, ^{Mendel et al. 2011}, ^{Aceves et al. 2015}). Earlier N-body simulations (e.g. ^{Barnes 1985}; Bode, Cohn & Lugger 1993) showed that a common massive dark halo delayed the merging time of small groups, and later AMB97 reported on a large set of collision-less simulations, where they found that massive, non-concentrated common dark halos slowed the merging time; in particular if such a halo is in virial equilibrium, the groups can survive without merging for times longer than the Hubble time.

Several of the cosmological studies mentioned have shown that the observed number density of CGs is consistent with the statistics of compact grouplike associations in the current standard cosmological scenario (e.g. ^{McConnachie et al. 2008}, ^{Díaz-Giménez & Mamon 2010}, ^{Aceves et al. 2015}). Hence the overmerging problem of CGs, inferred from their small crossing times, does not seem to pose a big problem for our current understanding of structure formation in the universe, even though they observationally have very small crossing times. For example, from the results of ^{Aceves et al. (2015)} it follows that compact group-like associations can arrive at the current epoch, in a natural way in a ΛCDM cosmology avoiding overmerging. In such a study it was found that compact associations of galaxy-size dark halos are in a stage of gravitational collapse, and that a non-cuspy and non-massive (< 20% of the total mass) common dark halo exists. This is a∼ likely situation that can represent what is actually happening in observed CGs at present.

Several works have addressed the topic of the future evolution of large-scale structures in the universe and of the Local Group of galaxies (e.g. ^{Loeb 2002}, ^{Busha et al. 2003}, ^{Hoffman et al. 2007}, ^{Cox & Loeb 2008}, ^{Araya-Melo et al. 2009}). At the moment, to our knowledge, the future fate of current compact configurations obtained directly from cosmological simulations has not been investigated. This would provide, among other things, an assessment of wheter an overmerging problem is expected to be happening just after the present epoch (and to what extent) or if a longer longevity of these systems is likely.

The purpose of the present work is to use the systems of galaxies, modeled as pure dark halos, that form a compact association (similar to the observed CGs) obtained from several cosmological simulations, and to follow their future dynamical evolution for the next 5 Gyr to study their longevity. For completeness, we provide some examples of the behavior of kinematical quantities of three representative CGs over their dynamical evolution.

The outline of the paper is as follows. In § 2 we describe the method used in this work, and provide some details of the simulations used, as well as criteria used to determine when a merger occurs. In § 3 we present our results and some discussion. In § 4 we provide some final comments and conclusions.

2. METHOD

3. RESULTS AND DISCUSSION

In this section we show the results of the dynamical simulations described above. In Figures 1-3 we show the evolution of the particle configuration for three representative cases (G4, G7, G9) out of the fourteen ones obtained in the simulations at different times. The figures are meant to schematically show of the evolution; no special weighting of the particles was used when plotting.

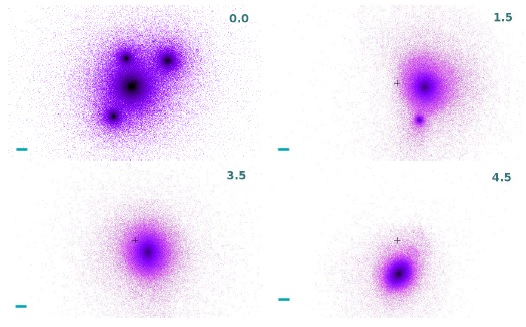
Fig. 1 Projected spatial dynamical evolution of the only CA (group G4) that forms a single massive remnant after about 5 Gyrs. The system is shown, from left to right and top to bottom, at t = {0.0,1.5,3.5,4.5}Gyr after the current epoch. The box dimension is 1 Mpc×1 Mpc. The bar scale on the lower left of each panel corresponds to 50kpc in length. 

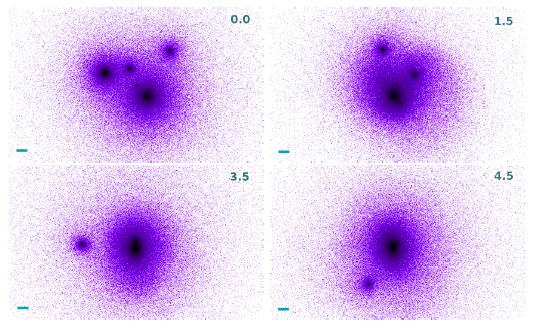
Fig. 2 Projection position of halos and intragroup matter similar to Figure 1, but here the end stage configuration results in a large dark halo and another halo in orbit around the first (group G7). 

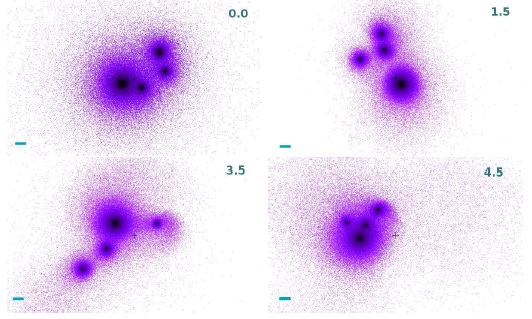
Fig. 3 Projected spatial configuration evolution, as in Figure 1, but in this case (group G9) no merger develops over 5 Gyr of evolution from the present. 

Figure 1 shows the projected evolution of the only group (G4, 1 out of 14) that suffers a complete merger in the 5 Gyr after the current epoch. At 1.5 Gyr there are only two halos noticeable, and at 3.5 Gyr a single object appears. A gravitational collapse of all material, both from individual halos or from intragroup matter, is present at 5 Gyr.

Figure 2 shows a sample of the evolution of a group (G7) where 2 objects are discernible at ≈ 5Gyr, and in Figure 3 we show a group (G9) where none of the halos merge in the time span of the dynamical evolution. Notice that even after 5 Gyr of dynamical evolution, in the groups of Figures 2 and 3 an appreciable amount of intragroup matter exists, contrary to the situation displayed in Figure 1.

In Figure 4 we show the merging history of our 14 CAs during 5 Gyr of dynamical evolution after the current epoch. Noticed that only one CA suffered a complete merger and in only one case no merger occurred in the time span of these simulations. Also, only one group had 5 members initially (G1). This group ended having 4 halos after suffering a binary merger. From this figure it follows that some CAs, even after 5 Gyr of evolution, might survive for a longer time and show still discernible halos.

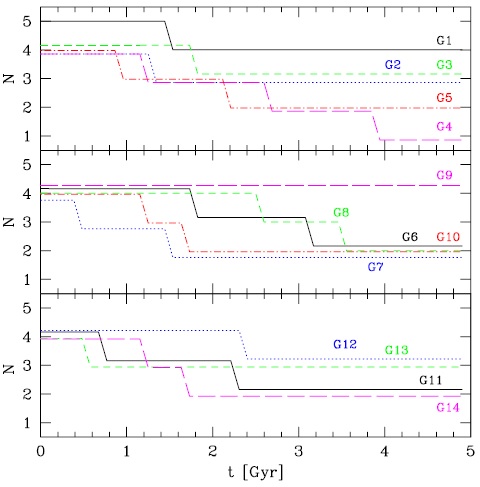
Fig. 4 Merger history of our 14 CAs. Only one CA had initially 5 galaxy-size dark halos, the rest all had 4 such members; a full merger is indicated when only N =1 object remains in the system. A single group (G4) coalesced into a single object and only other group (G9) survived without any merger in 5 Gyr. 

The relatively small number of CAs studied in this work precludes us from making any statistically significant estimate of the number of currently observed compact groups (at z ≈ 0) that could resist total merging in the next five giga-years. Nonetheless, it seems from the results presented here that such a number might not be very different from 10% of the total number of observed compact groups.

On other hand, from Figure 4 it follows that it is highly probable that none of the true compact groups observed (at z = 0) will suffer a complete merger within the next ≈ 1Gyr, even if they are in the process of gravitational collapse. Only four of the fourteen initial CAs (≈ 30%) suffer a binary merger in approximately the next giga-year. Probably half of them will survive at least for another 3 Gyrs without a complete merger.

The results obtained here indicate that there is no risk of an overmerging problem to occur in the near future in observed CGs, in so far as the model used here resembles the actual situation of observational counterparts.

In the case where a complete merger occurs, as shown in Figure 1, a large concentration of dark matter is present, with a minimal large envelope, but the subsequent dynamical evolution of that system was not explored. The other cases where an incomplete full merger is achieved, the amount of intragroup matter is more noticeable. No clear physical boundary for a halo can be established in these dynamical simulations, since its gravitational potential does not tend to zero away from the center of each dark halo inside the group, before encompassing another halo; this is a necessary condition to compute a gravitational radius.

Some kinematical quantities of the CAs shown in Figures 1-3, such as the crossing time (τ_c), projected harmonic radii (R_H), one-dimensional velocity dispersions (σ) and total inferred “virial masses” (M_vir) are displayed in Figure 5. The definitions used to compute these quantities are those in ^{Aceves & Velázquez (2002)}, following common observational estimators:

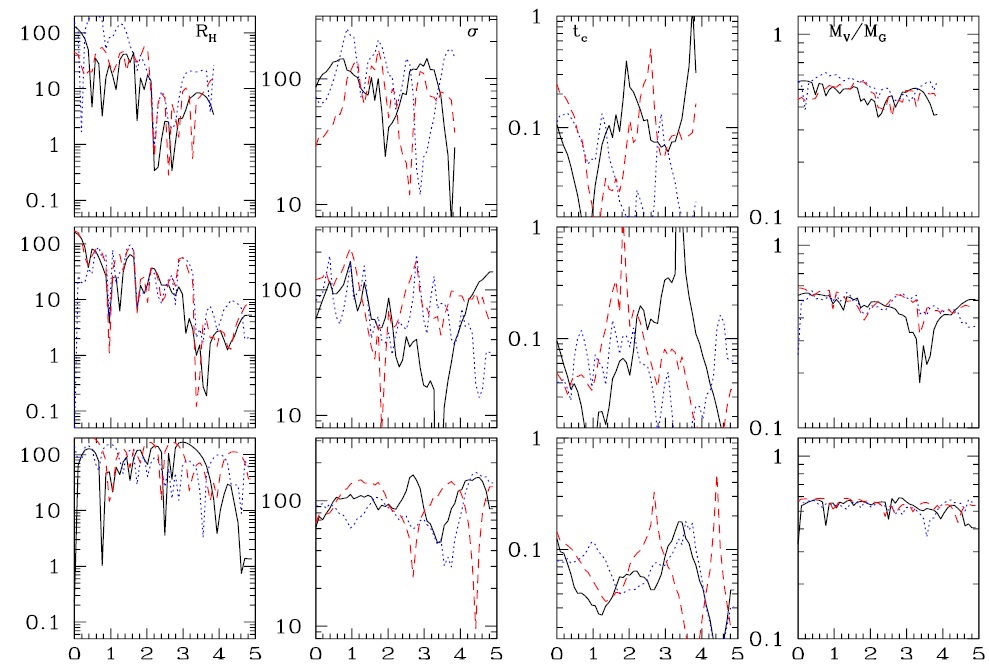
Fig. 5 Kinematical quantities for CAs in Figures 1-3 (groups G4, G7 and G9) from top to bottom row, respectively, are shown. The projected harmonic radius, RH, the one-dimensional velocity dispersion along each “line-of-sight” σ, the crossing time tc = 4R/(π3σ) (R being the mean projected separation), and the virial mass estimator Mv normalized to the total actual mass of the gravitational system; this mass is not to be confused with the one shown in Table 1. Different line styles indicate different line-of-sights. For group G4 the computation of the observationally related quantities end when a full group merger is signaled. 

where R,R_ij and N_g are the average projected separation, the projected separation between galaxy pairs and the number of galaxies, respectively. The virial mass was calculated following ^{Heisler et al. (1985)}:

Here, V _i is the velocity along the line of sight with respect to the velocity centroid. To compute such quantities, the bulk motions of the dark halos inside the physical group were used. The values shown for these CAs are representative of the observed CGs, and two things are worth mentioning here. On the one hand, the average mass of a CG is probably underestimated since (assuming this evolutionary scenario is correct) since the M_v estimator is about 50% of the total mass of the bound group mass. This has repercussions on the mass estimates obtained for such systems using typical virial when a full group merger is signaled.

mass estimators, as suggested in an early studies (e.g. ^{Barnes 1985}, ^{Aceves & Velázquez 2002}), This needs to be taken into consideration when addressing such problems.On the other hand, the small values of the crossing times obtained for our models of CGs ( ≲0.1H0-1) support earlier work (^{Barnes 1985}, ^{Aceves & Velázquez 2002}) in that one can hardly assure that a small group of galaxies is in virial equilibrium, or that it is close to having a full merger of its members if a small crossing time is calculated. Hence, the problem of determining which actual observed CGs might suffer a complete merger (or even a binary merger) in the near future does not seem to be straightforward. Some peaks of large values of the crossing time t_c are noticed in Figure 5, which correspond to cases where some mergers are occurring, leading to very small σ values.

4. FINAL COMMENTS

The longevity of present CAs formed by galaxylike size dark halos immersed in common dark halos obtained from cosmological simulations, was studied using dynamical N-body simulations.

The initial conditions for the CAs used in this work were obtained from previously reported ΛCDM cosmological simulations (^{Aceves et al. 2015}) where, in particular, it was found that a non-massive (≲ 20%), collapsing and non-cuspy distribution encompasses a set of galaxy-like objects resembling compact groups.

The present work used normal galaxy-like size dark halos to model galaxies in environments that mimic observed CGs. The use of pure N-body simulations as well as the use of only spherical halos to represent galaxies in such environments has been studied in the past (e.g. ^{Carnevali et al. 1981}, ^{Ishizawa et al. 1983}, ^{Barnes 1985}, Governato et al. 1991, Bode et al. 1993, AMB97, ^{Aceves & Vea´zquez 2002}, ^{Taranu et al. 2013}), and has led to important insights in the evolution of CGs. Concerning the purpose of this work, the use of such a halo model to represent galaxies appears well justified.

The main result of this work indicates that the currently observed compact groups of galaxies, in general, will not suffer a complete merger within roughly the next 5 Gyr, roughly half the age of the universe. In particular, our results suggest that most current observed CGs will undergo 1-2 mergers, and nearly half of them will end up with 2 members. Hence, present compact groups probably have a long time to further evolve despite indications to the contrary, as their present small crossing times.

The near future overmerging of present CAs does not seem to be a problem for these systems. It may be that the dynamical friction timescales are much larger than the crossing times. However, no reliable estimation of the former timescale can be done because “galaxies” are not point particles and the intragroup medium is not homogeneous; in practice one would need to do an N-body simulation calibration of the Chandrasekhar formula for the dynamical friction timescale (e.g. ^{Inoue 2011}).

A limitation of our work is the small number of CGs considered, that precludes us to obtain statistically significant results. Another one is the resolution in mass of our simulations, in particular, for the IG particles. Clearly a larger number of cosmological simulations, including some re-zooming techniques and a disk component in some dark halos, would alleviate some of these limitations. An orbital analysis of those current compact associations that will not suffer a full merger in the near future could provide more insight into the dynamical conditions for avoiding overmerging. Unfortunately, such analysis is beyond the scope of this paper, as are topics such as the structure of the merger remnants of spiral-like galaxies or the effects of gas on star formation, but future studies are planned.