1. Introduction
Although the primary aim of the Kepler mission is to detect transiting planets by obtaining very high precision photometric measurements, it provides further benefits, especially in terms of clear and reliable determination of very small amplitude light variations on eclipsing and intrinsic variable stars. About 150000 targets have been observed in the mission, and apart from the exoplanets, numerous variable stars have been discovered. The unprecedented precision of the Kepler photometry clearly revealed low amplitude (mmag) light variations, which were used in the analysis of stellar flares, spot activity and differential rotation (Balona 2015; Balona et al. 2016; Reinhold & Reiners 2013; Reinhold et al. 2013a). Among these variable stars, 2876 eclipsing binary stars have been discovered (Prša et al. 2011; Slawson et al. 2011). Careful light curve modelling of the binaries with cool components (Teff < 6500 K) revealed rotational modulation of the light curves and flares in model residuals. KIC 09641031 (Yolda ̧s & Dal 2016), KIC09761199 (Yolda ̧s & Dal 2017) and KIC2557430 (Kamil & Dal 2017), GJ1243, GJ 1245A and B (Hawley et al. 2014), KIC 2300039, KIC4671547 (Balona 2015) are examples of such stars.
The analyses of the patterns of magnetic activity exhibited by these stars reveal some clues about their evolutionary stages. Although there are several indicators found in these analyses, two of them are the energy spectra defined by Gershberg (1972) and the flare frequencies described by Ishida et al. (1991). Both of them have been computed, especially from the 1970’s to the 1980’s, in order to figure out the magnetic activity levels for the stars with detected flares. In 1990’s, Leto et al. (1997) examined the flare frequency variation of EV Lac, a well-known UV Ceti type star. There are a few studies on the activity levels of three magnetic active stars discovered in the Kepler Mission depending on their flare frequencies. Yolda ̧s & Dal (2016) detected 240 flares from KIC09641031, and Yolda ̧s & Dal (2017) detected 94 flares from KIC09761199. In addition, Kamil & Dal (2017) detected 69 flares from KIC2557430. Yolda ̧s & Dal (2016) derived the one phase exponential association (hereafter OPEA) model, and the flare frequency N1 was found to be 0.41632 h-1 for KIC09641031. Yolda ̧s & Dal (2017) computed N1 as 0.01351 h-1 for 69 flares for KIC 09761199. However, an interesting situation occurs in the case of KIC2557430. Kamil & Dal (2017) find that some of the flares detected from KIC 2557430 come from a third body; it is unclear whether it is a component in the system or an undetected background light source. Depending on the OPEA model derived from 69 flares, Kamil & Dal (2017) reveal that 40 (called Group 1) of them come from the secondary component, while 29 flares (called Group 2) come from a third body. They computed the flare frequency N1 as 0.02726 h-1 for Group 1 and 0.01977 h-1 for Group 2. As discussed by Yolda ̧s & Dal (2016) and Gershberg (2005), the flare frequency is one of the parameters indicating the nature of the flare mechanism in the stellar atmosphere. Apart from the classical parameters described by Gershberg (2005), Dal & Evren (2010, 2011) have also described some new parameters derived from the OPEA models in order to determine the flare process occurring on the stellar surface.
Continuous photometry of variable single stars discovered by Kepler enabled to trace photometric period variations as a proxy of differential rotation via Fourier transform (see, e.g. Reinhold et al. 2013b; Reinhold & Reiners 2013). However, the Fourier transform may not perfectly work in case of eclipsing binaries, where the amplitude of the rotational modulation of star spots is usually embedded into the relatively large amplitude light variations caused by eclipses and the lack of spherical symmetry of the binary components. Furthermore, insufficient representation of light curve models, especially around mid-eclipse phases, may require discarding data around those phases and may cause regular gaps in the light curve, which would lead to unwanted alias periods and harmonics. In this case, alternative methods should be adopted to trace photometric period variation, such as an O − C diagram based on minimum times of rotationally modulated light curves (see, e.g. özdarcan et al. 2010).
In the case of eclipsing binary stars, additional intrinsic variations may not be determined at first, due to the reasons explained above. KIC 9451096 is such an eclipsing binary in the Kepler eclipsing binary catalog1 (Prša et al. 2011; Slawson et al. 2011) with a short period, and with a confirmed third body (Borkovits et al. 2016). Beyond the properties provided by the catalog, such as morphology and eclipse depths, Armstrong et al. (2014) provided physical information, estimated from the spectral energy distribution based on photometric measurements. They estimated the effective temperature of the components of KIC 9451096 as 7166 K and 5729 K for the primary and the secondary component, respectively.
In this study, we carry out a photometric and spectroscopic analysis of KIC 9451096, based on Kepler photometry and optical spectroscopic observations with intermediate resolution described in § 2. § 3 describes the spectroscopic and photometric modelling of the system, and the analysis of the out-of-eclipse variations. In the final section, we summarize and discuss our findings.
2. Observations and data reductions
2.1. Kepler Photometry
Photometric data obtained by the Kepler spacecraft cover a broad wavelength range between 4100 ̊A and 9100 ̊A; this has the advantage of collecting many more photons in a single exposure and reaching sub-milli-mag precision, but also has the disadvantage of having no “true” photometric filter, hence no photometric color information. There are two types of photometric data having different exposure times. These are short cadence data (having an exposure time of 58.89 seconds) and long cadence data (having an exposure time of 29.4 minutes). In this study we use long cadence data of KIC 9451096 obtained from the Kepler eclipsing binary catalog. The catalog provides detrended and normalized intensities, which are obtained by application of procedures described by Slawson et al. (2011) and Prša et al. (2011). The whole data covers ≈4 years of time, with 65307 data points in total. The MAST archive reports 0.9% contamination level in the measurements, practically indicating no additional light contribution to the measured fluxes of KIC 9451096.
2.2. Spectroscopy
We obtained optical spectra of KIC 9451096 with the 1.5 m Russian - Turkish telescope equipped with the Turkish Faint Object Spectrograph Camera2 (TFOSC) at Tubitak National Observatory. TFOSC enables one to obtain intermediate resolution optical spectra inéchelle mode. In our case, the instrumental setup provides actual resolution of R = λ/∆λ ≈ 2800 around 6500 ̊A, and the observed spectra cover a usable wavelength range between 3900-9100 ̊A in 11 échelle orders. A back illuminated 2048 × 2048 pixels CCD camera, which has pixel size of 15 × 15 μm2, was used to record spectra.
We obtained ten optical spectra of KIC9451096 during the 2014 and 2016 observing seasons. In order to obtain enough signal, we used 3600 s of exposure time for each observation. The estimated signal-to-noise ratio (SNR) of observed spectra is mostly between 80-100, except for a few cases, where the SNR is around 50. SNR estimation is based on photon statistic. Together with the target star, we also obtained high SNR optical spectra of HD 225239 (G2V, vr = 4.80 km s-1) and ι Psc (HD 222368, F7V, vr = 5.656 km s-1), and adopted them as radial velocity and spectroscopic comparison templates.
We reduced all observations using standard IRAF3 packages and tasks. A typical reduction procedure starts with obtaining a master bias frame from several bias frames taken nightly, and subtracting the master bias frame from all object, calibration lamp (Fe-Ar spectra in our case) and halogen lamp frames. Then the bias corrected halogen frames are combined to form an average halogen frame and this average frame is normalized to unity to produce the normalized master flat frame. After that, all target and calibration lamp spectra are divided by the normalized flat field frame. Next, cosmic rays removal and scattered light corrections are applied to the bias and flat corrected frames. At the end of these steps, reduced frames are obtained and these frames are used for the extraction of spectra. In the final steps, Fe-Ar frames are used for wavelength calibration of the extracted spectra and the wavelength calibrated spectra are normalized to unity by using cubic spline functions.
3. Analysis
3.1. Radial Velocities and Spectroscopic Orbit
The first step of our analysis is to determine the radial velocities of the components and the spectroscopic orbit of the system. We cross-correlated each observed spectrum of KIC9451096 with spectra of template stars HD 225239 and ι Psc, as described in Tonry & Davis (1979). In practice we used the fxcor task in IRAF environment. We achieved better cross-correlation signals (especially for the weak secondary component) when we used HD 225239 as template; thus, we determined all radial velocities with respect to the HD225239 spectrum. We obtained acceptable cross-correlation signals of both components inéchelle orders 5 and 6, which cover a wavelength range between 4900-5700 ̊A. Figure 1 shows the cross-correlation functions of two spectra obtained around orbital quadratures.
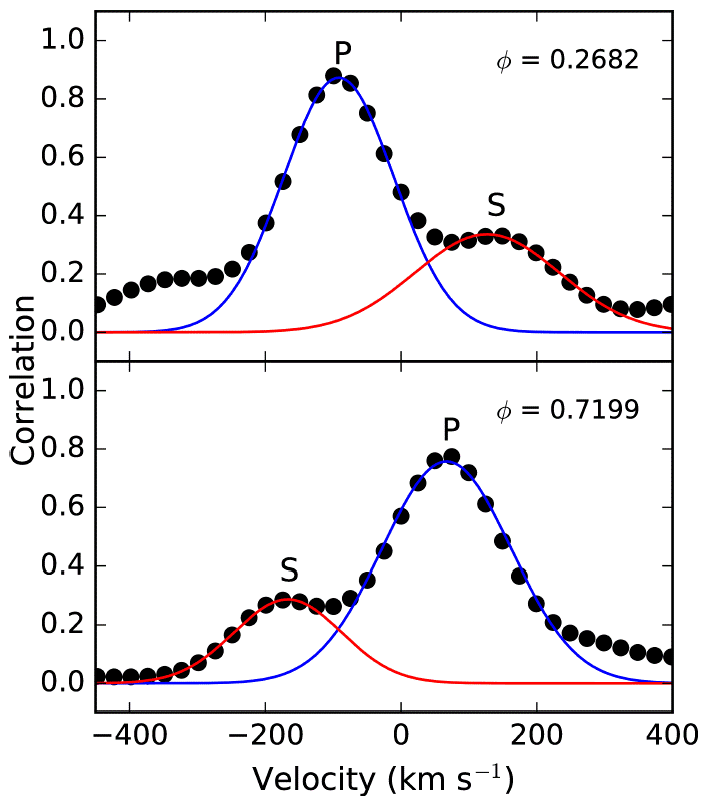
Fig. 1 Cross-correlation functions of two spectra obtained around orbital quadratures. The letter ϕ denotes corresponding orbital phase. P and S indicate the primary component and the secondary component, respectively.
We list the observation log and the measured radial velocities of the components in Table 1. Note that we use the ephemeris and period given by Borkovits et al. (2016) and listed in their Table 2 to calculate orbital phases and for further analysis.
Table 1 Log of spectroscopic observations*
| HJD | Orbital | Exposure | Primary | Secondary | ||
|---|---|---|---|---|---|---|
| (24 00000+) | Phase | time (s) | Vr | σ | Vr | σ |
| 56842.5435 | 0.7794 | 3600 | 91.4 | 8.2 | -152.5 | 36.9 |
| 56844.4052 | 0.2682 | 3600 | -79.9 | 6.3 | 151.9 | 39.1 |
| 56844.4479 | 0.3024 | 3600 | -74.4 | 6.6 | 155.0 | 37.2 |
| 56889.4315 | 0.2781 | 3600 | -77.1 | 5.7 | 148.1 | 40.0 |
| 56890.2958 | 0.9693 | 3600 | 14.5 | 5.0 | - | - |
| 57591.4532 | 0.7199 | 3600 | 88.5 | 7.2 | -153.3 | 32.0 |
| 57601.4386 | 0.7058 | 3600 | 88.7 | 5.4 | -149.8 | 32.1 |
| 57616.4778 | 0.7333 | 3600 | 86.0 | 4.3 | -145.2 | 38.7 |
| 57617.5188 | 0.5659 | 3600 | 31.0 | 5.8 | - | - |
| 57672.3009 | 0.3779 | 3600 | -54.8 | 5.1 | 111.1 | 47.9 |
*together with measured radial velocities and their corresponding standard errors (σ) in kms−1.
Table 2 Spectroscopic orbital elements of KIC 9451096. *
| Parameter | Value |
|---|---|
| Porb (day) | 1.25039069 (fixed) |
| T0 (HJD24 00000+) | 54954.72942 (fixed) |
| (kms−1) | 2.8±0.5 |
| K1 (kms−1) | 84.1±2.3 |
| K2 (kms−1) | 153.2±14.6 |
| e | 0 (fixed) |
| a sin i (R⊙) | 5.92±0.35 |
| M sin3 i (M⊙) | 1.79±0.25 |
| Mass ratio (q = M2/M1) | 0.55±0.05 |
| rms1 (kms−1) | 3.7 |
| rms2 (kms−1) | 4.9 |
*M1 and M2 denote the masses of the primary and the secondary component, respectively, while M shows the total mass of the system.
We achieved a reasonable solution for the spectroscopic orbit assuming zero eccentricity, where an undefined longitude of periastron is taken. We checked this assumption by inspecting the Kepler light curve of the system, where we observe deeper and shallower eclipses at 0.0 and 0.5 orbital phases, respectively, indicating a circular orbit (see § 3.3, Figure 4). In order to reach the final spectroscopic orbital solution, we prepared a simple script written in Python language, which applies Markov chain Monte Carlo simulations to the measured radial velocities, considering their measured errors. We list the final spectroscopic orbital elements in Table 2 and plot the measured radial velocities, their observational errors, the theoretical spectroscopic orbit and residuals from the solution in Figure 2.
3.2. Spectral Type
We rely on our intermediate resolution TFOSC optical spectra to determine the spectral type of the components. Most of our spectra correspond to the phases around orbital quadratures, where we observe the signal of the two components separated. However, there are two spectra obtained at phases close to the eclipses, where the two components can not be resolved separately. One of these spectra corresponds to ≈ 0.56 orbital phase (see Table 1), where we cannot observe the radial velocity signal of the secondary component in cross-correlation. Even at the orbital quadratures, the cross-correlation signal of the secondary component is considerably weak compared to the primary component, indicating a very small light contribution from the secondary component to the total light of the system. Our preliminary light curve analysis shows that the contribution of the secondary component to the total light does not exceed ≈ 10%. In this case, the signal from the secondary component becomes almost negligible at the resolution of our observed spectrum at ≈ 0.56 orbital phase. Therefore, we assume that we only observe the spectrum of the primary component and adopt this spectrum as reference spectrum for the primary component. We confirm this assumption by calculating the composite spectrum of the binary via final parameters of the components (see § 3.3), where we observe that the contribution of the secondary component affects the theoretical composite spectrum less than 2% for the wavelength range of 4900-5700 ̊A. We refrain from performing a detailed analysis with spectral disentangling. Future studies could take advantage of this technique and derive atmospheric parameters of the secondary.
We first compare the reference spectrum with the template spectra of HD 225239 and ι Psc. We observe that ιPsc spectrum provides a closer match to the reference spectrum but also indicates earlier spectral type and slightly lower metal abundances for the primary component. At that point, we switch to the spectrum synthesizing method. We use the latest version of python framework iSpec (Blanco-Cuaresma et al. 2014) which enables practical and quick calculation of a synthetic spectrum with a given set of atmospheric parameters via different radiative transfer codes. Among these codes we adopt the SPECTRUM4 code (Gray & Corbally 1994), together with ATLAS-9 (Castelli & Kurucz 2004) model atmospheres and the actual line list from the third version of the Vienna atomic line database (V ALD3, Ryabchikova et al. 2015).
Considering the spectral type of ι Psc, we synthesize spectra for effective temperatures between 6000 K and 7000 K in steps of 250 K, and metallicity values ([Fe/H]) between −1.0 and 0.0 in steps of 0.5. For all synthetic spectra we fix the gravity (log g) to 4.15, which we precisely calculate by light curve modelling (see § 3.3). Since we do not have a high resolution spectrum, we fix the microturbulence velocity to 2 kms-1. We convolve all calculated spectra with a proper Gaussian line spread function in order to degrade their resolution to the resolution of the TFOSC spectra. Instrumental broadening in TFOSC spectra is 2.2 ̊A, corresponding 119 km s-1 for wavelengths around 5500 ̊A. The estimated projected rotational velocities of the components are 62 km s-1 and 36 km s-1 for the primary and the secondary component respectively (see § 3.3). Since instrumental broadening is the most dominant broadening source in the observed spectra, we do not consider rotational broadening and other line broadening mechanisms.
Among the calculated spectra we find that the model with 6500 K effective temperature and an [Fe/H] value of −0.5 provides the closest match to the reference spectrum. The final effective temperature indicates F5 spectral type (Gray 2005). Considering the effective temperature and metallicity steps in model atmospheres, and the resolution of TFOSC spectra, the final values and their estimated uncertainties are Teff = 6500±200 K and [Fe/H] = −0.5±0.5 dex, respectively. Note that even if we considered the neglected contribution of the secondary component in the reference spectrum, its effect would be within the estimated uncertainties above. The final Teff value is ≈ 670 K lower than the 7166 K value estimated in Armstrong et al. (2014). In Figure 3 we show portions of the reference spectrum and the model spectrum, calculated with the final parameters above.
3.3. Light Curve Modelling and Physical Properties
Global visual inspection of KIC 9451096 Kepler photometry reflects properties of a typical close eclipsing binary. We start the light curve modelling by phasing the whole long cadence data with respect to the ephemeris and period given by Borkovits et al. (2016), and re-binning the phased data with a phase step of 0.002 via the freely the available fortran code lcbin5 written by John Southworth. We plot the binned and phased light curves of the system in Figure 4, panels a and aa. The light curve indicates a detached configuration for the system. Mid-eclipse phases are 0.0 and 0.5 phases, indicating a circular orbit. There is no conspicuous asymmetry in the light curve.
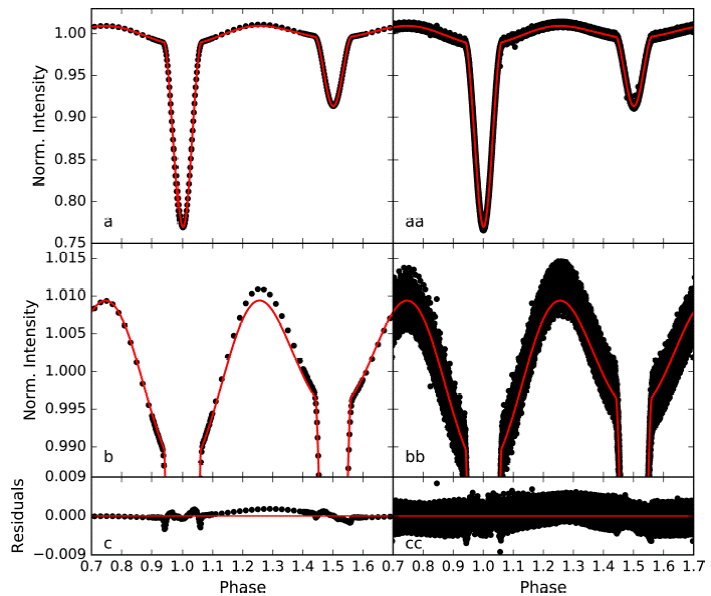
Fig. 4 (a) Phase binned light curve of KIC9451096 (black filled circles) together with best-fitting model (red curves). (b) Close up view of the light curve at light maxima. c) Residuals from the best-fitting model. Panels at right (aa, bb and cc) are the same as left panels but for phased long cadence data. The color figure can be viewed online.
We model the light curve with the 2015 version of the Wilson-Devinney code (Wilson & Devinney 1971; Wilson & Van Hamme 2014). In the modelling, we first fix the most critical two parameters of the light curve modelling, i.e., the mass ratio (q) of the system and the effective temperature of the primary component (T1). Since we have reliably derived these parameters in previous sections as q = 0.55 and T1 = 6500 K, we adopt them as fixed parameters. The calculated atmospheric properties of the primary component reveal that both stars have convective envelopes. Therefore, we set albedo (A1 , A2 ) and gravity darkening (g1, g2) coefficients of the components to 0.5 and 0.32, respectively, which are typical values for stars with convective outer envelopes. We also consider a slight metal deficiency of the system, and thus adopt the internal stellar atmosphere formulation of the Wilson-Devinney code according to the determined [Fe/H] value of −0.5. We assume that the rotation of the components is synchronous with the orbital motion, and thus fix the rotation parameter of each component (F1 , F2 ) to 1.0. We adopt a square root law (Klinglesmith & Sobieski 1970) for limb darkening of each component; this is more appropriate for stars cooler than 9000 K. We take the limb darkening coefficients for the Kepler passband (x1, x2, y1, y2) and the bolometric coefficients (x1bol , x2bol , y1bol , y2bol ) from van Hamme (1993). In the modelling, we adjust inclination of the orbit (i), temperature of the secondary component (T2), dimensionless omega potentials of the components (Ω1, Ω2) and luminosity of the primary component (L1). We also include a phase shift parameter as adjustable in the modelling, since we expect a shift in the ephemeris due to the light-time effect of the third body (Borkovits et al. 2016). The model quickly converged to a steady solution in a few iterations. We list the model output in Table 3 and we plot the best-fitting model in Figure 4, panels a, b, and the residuals from the model in panel c.
Table 3 Light curve modelling results of KIC9451096.a
| Parameter | Value |
|---|---|
| q | 0.55* |
| T1(K) | 6500* |
| g1, g2 | 0.32*, 0.32* |
| A1, A2 | 0.5*, 0.5* |
| F1 = F2 | 1.0* |
| phase shift | 0.00108(2) |
| i (◦) | 79.07(4) |
| T2(K) | 5044(200) |
| Ω1 | 4.4942(49) |
| Ω2 | 4.8885(125) |
| L1/(L1+L2) | 0.897(1) |
| x1bol, x2bol | 0.136*, 0.293* |
| y1bol, y2bol | 0.583*, 0.401* |
| x1, x2 | 0.106*, 0.482* |
| y1, y2 | 0.670*, 0.313* |
| (r1),(r2) | 0.2557(3), 0.1506(5) |
| Model rms | 3.0 × 10−4 |
a(r1),(r2) denote the mean fractional radii of the primary and the secondary components, respectively. Internal errors of the adjusted parameters are given in parentheses for the last digits. Asterisk symbols in the table denote fixed values for the corresponding parameter. Note that we adopt the uncertainty of T1 for T2 as well, since the internal error of T2 is unrealistically small (∼1 K).
In Figure 4, panel b, one can easily see the model inconsistency around 0.25 orbital phase. The inconsistency indicates an additional light variation, which is known as O´Connell effect, i.e. difference between light levels of subsequent maxima in an orbital cycle. Possible sources of the difference may be Doppler beaming, a hot spot or a cool spot on one of the component of the system. KIC9451096 is a detached eclipsing binary, thus we can safely exclude possibility of mass transfer between components, i.e., a hot spot possibility. Doppler beaming was detected observationally among some Kepler binaries (see, e.g. van Kerkwijk et al. 2010), which becomes important for systems with very low mass ratios, especially for systems with a compact component, such as a white dwarf or a hot sub-dwarf. In addition, if the effect is in progress, then it would change the light levels of each maxima. However, we observe inconsistency only for phase 0.25, while the model fairly represents the light level at phase 0.75. Thus, Doppler beaming should have a negligible effect in the case of KIC 9451096, if any. A remaining possibility is cool spots located preferably on the cooler component.
Here we do not chose to model this inconsistency alone, which would only show the cumulative effect of hundreds of light curves, but instead we subtract the best-fitting model from the whole long cadence data and inspect the residuals in order to investigate further light variations. We will focus on this in § 3.4.
We complete the light curve modelling section with a calculation of the absolute parameters of the system by combining the spectroscopic orbital solution and light curve model results. In Table 4, we give the physical properties of each component. Our analysis reveals that the system is formed by an F5V primary and a K2V secondary component.
Table 4 Absolute physical properties of KIC9451096.*
| Parameter | Primary | Secondary |
|---|---|---|
| Spectral Type | F5V | K2V |
| [Fe/H] | −0.5 ± 0.5 | |
| Mass (M⊙) | 1.18(26) | 0.65(9) |
| Radius (R⊙) | 1.53(10) | 0.90(6) |
| Log L/L⊙ | 0.574(76) | −0.327(88) |
| log g (cgs) | 4.14(4) | 4.34(1) |
| Mbol (mag) | 3.31(19) | 5.57(22) |
*The error of each parameter is given in parantheses for the last digits.
3.4. The Out-of-Eclipse Variations
In this section, we subtract the best-fitting light curve model from the whole long cadence data and obtain residuals. Here, we first divide the whole long cadence data into subsets, where each subset covers only a single orbital cycle, resulting in 1026 individual light curves. Then we apply the differential corrections routine of the Wilson-Devinney code and fix all parameters, except the ephemeris reference time. In this way, we find a precise ephemeris reference time for each individual subset, therefore eliminating any shift in the ephemeris time due to the third body reported by Borkovits et al. (2016), and obtain precise residuals. In Figure 5, we plot three different parts of the residuals. Note that we remove data points that correspond to the eclipse phases due to the insufficient representation of the model at those phases. This mainly arises from the inadequacy of radiative physics used in light curve modelling for a very high photometric precision and can clearly be seen in Figure 4 panel c.
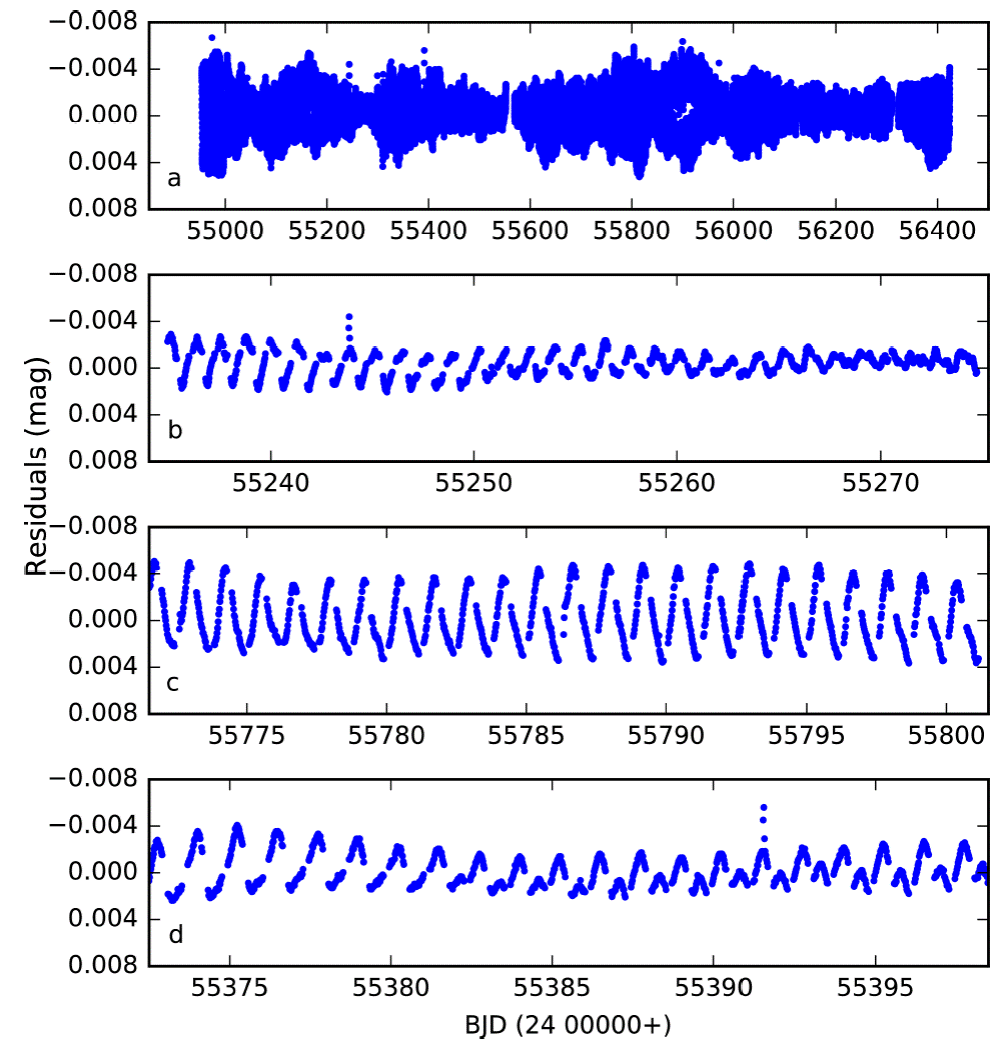
Fig. 5 (a) Residuals from whole long cadence data. Remaining panels show different time ranges of residuals, where we observe different light curve shapes, and flares.
Inspecting residual brightness, we immediately see a variation pattern which changes its shape from time to time. Furthermore, we observe a sudden increase and gradual decrease in the residual brightness which occasionally occurs over four years of time span and has short time scale of a few hours. These patterns are traces of magnetic spot activity, which is very possible for the K2V secondary component. Observational confirmation of this possibility can be done by inspecting magnetic activity sensitive spectral lines, such as the Hα and Ca II H & K lines. We inspected these lines in our TFOSC spectra and did not notice any emission features, which could be considered as the sign of the activity. However, one should consider that the contribution of the secondary component to the total light does not exceed 10% at optical wavelengths and will steeply decrease towards the ultraviolet region of the spectrum. Furthermore, the variation patterns observed in Figure 5 exhibit very small amplitudes. Therefore, the existence of magnetic spot activity cannot be confirmed or excluded via spectral line inspection in the case of KIC 9451096. Nevertheless, variation patterns and flares observed in the residuals indicate weak magnetic spot activity in the secondary component, which can still be detected with the very high precision of the Kepler photometry.
We analyze rotational modulation and flares of the secondary component via residuals by assuming that the source of all variation patterns is only the secondary component.
3.4.1. Photometric Period and Differential Rotation
Conventional periodogram methods for determining rotational period do not perfectly work in our case because the observed variation patterns exhibit quick changes in amplitude and mean brightness level over short time scales of a few days, which is comparable to the orbital period. Moreover, since we remove data points at eclipse phases, this causes regular gaps in the data which repeat each ≈ 0.625 day (i.e. half of the orbital period); thus, it causes an alias period and its harmonics, and disturbs the real periods. Furthermore, one can clearly see that the rotational modulation of residuals has an asymmetric shape. Considering an individual light curve with an asymmetric shape, it is not possible to find a single period to represent the whole light curve perfectly, and additional periods (i.e. harmonics) are required. Therefore we apply an alternative method based on tracing the time of a minimum light observed in an orbital cycle, which was previously applied to RS CVn system HD 208472 (özdarcan et al. 2010). For each orbital cycle, we find the time of the deepest minimum in the cycle by fitting a second or third order polynomial to the data points around the expected minimum time. The order of the polyno Subset mial depends on the light curve shape. After obtaining all minimum times, we construct an O − C diagram by adopting the first minimum time observed in the residuals as initial ephemeris reference time, and the orbital period as the initial period, and obtain O−CI values. Then we apply a linear fit to the O−CI values and calculate an average ephemeris reference time and period given in Equation 1, together 6 with statistical uncertainties given in parentheses for the last digits.
In the equation, T0(BJD) and E denote ephemeris reference time and integer cycle number, respectively. We plot O − CI values and linear fit in Figure 6, panel a. After obtaining an average ephemeris and period, we subtract the linear fit from O−CI data and obtain O−CII data, which in principle shows the real period variation for a given time range. Figure 6, panel b shows O − CII data. We divide O − CII data into 30 subsets by grouping data points that appear with a linear slope. The linear trend of a subset gives the difference between the best-fitting photometric period of the subset and the grand average photometric period given in Equation 1. Therefore we can calculate a mean photometric period for each subset. We plot the calculated mean photometric periods versus time in Figure 6, panel c, together with the statistical uncertainties. We list photometric periods for 30 subsets in Table 5, and tabulate our O − C analysis results in Table 8.
Table 5 photometric periods found from O − C analysis
| Subset | BJD (24 00000+) | P (day) | σ(P) (day) |
|---|---|---|---|
| 1 | 54994.8107 | 1.2456 | 0.0004 |
| 2 | 55048.8731 | 1.2326 | 0.0008 |
| 3 | 55094.1598 | 1.2441 | 0.0004 |
| 4 | 55139.0644 | 1.2260 | 0.0019 |
| 5 | 55169.9192 | 1.2459 | 0.0008 |
| 6 | 55208.0721 | 1.2489 | 0.0006 |
| 7 | 55250.0831 | 1.2584 | 0.0011 |
| 8 | 55314.8252 | 1.2484 | 0.0004 |
| 9 | 55366.4562 | 1.2355 | 0.0006 |
| 10 | 55425.0957 | 1.2470 | 0.0006 |
| 11 | 55478.0779 | 1.2517 | 0.0010 |
| 12 | 55507.4240 | 1.2437 | 0.0006 |
| 13 | 55539.3828 | 1.2216 | 0.0025 |
| 14 | 55629.1787 | 1.2430 | 0.0004 |
| 15 | 55702.5236 | 1.2447 | 0.0004 |
| 16 | 55740.2684 | 1.2522 | 0.0007 |
| 17 | 55793.0150 | 1.2485 | 0.0004 |
| 18 | 55840.9410 | 1.2223 | 0.0022 |
| 19 | 55868.2947 | 1.2534 | 0.0005 |
| 20 | 55894.6874 | 1.2712 | 0.0022 |
| 21 | 55924.7567 | 1.2494 | 0.0006 |
| 22 | 55960.4676 | 1.2391 | 0.0011 |
| 23 | 55996.8636 | 1.2507 | 0.0005 |
| 24 | 56026.2172 | 1.2474 | 0.0009 |
| 25 | 56073.0738 | 1.2528 | 0.0005 |
| 26 | 56136.3924 | 1.2449 | 0.0005 |
| 27 | 56258.6328 | 1.2509 | 0.0004 |
| 28 | 56333.3104 | 1.2323 | 0.0019 |
| 29 | 56359.5423 | 1.2565 | 0.0008 |
| 30 | 56400.8932 | 1.2504 | 0.0004 |
The average period given in Equation 1 represents the average rotation period for magnetic activity features on the surface of the secondary component, which are typically cool and dark regions, i.e., star spots, and indicates a slightly (∼0.5% day) shorter period compared to the orbital period. This is clearly observed in Figure 6 panel c, where the mean photometric periods of subsets are mostly shorter than the orbital period. Assuming a solar type differential rotation, this means that the orbital period is slightly longer than the equatorial rotation period of the secondary component. Under the same assumption, the differential rotation coefficient can be estimated from (Pmax −Pmin)/Pequ = kf, where Pmax , Pmin , k and f denote observed maximum and minimum period, differential rotation coefficient and a constant that depends on the range of spot forming latitudes, respectively (Hall & Busby 1990). Considering the small amplitude of rotational modulation of residuals, we assume that the secondary component is not largely spotted and that the total latitudinal range of the spot distribution is 45 degrees, which causes the f constant to take values between 0.5 and 0.7 (Hall & Busby 1990). Using maximum and minimum photometric periods from the O − C analysis, and assuming that the shortest period corresponds to the equatorial rotation period of the star, we find k = 0.081 ± 0.011 and k = 0.058 ± 0.006 for f = 0.5 and f = 0.7, respectively. Since these k values are calculated via boundary values of f, the real differential rotation coefficient must lie in the range of k values calculated above. An average k is found as 0.069±0.008.
3.4.2. Flares
We detect 13 flares in the residuals from long cadence data. In the flare analysis, it is critical to determine the quiescent level, which denotes the brightness level in the absence of a flare. In our case, we determine the quiescent level by applying Fourier analysis to the single orbital cycle where the flare occurs. The Fourier analysis represents the rotational modulation of residuals in the cycle, and then we remove the Fourier representation from the data. The remaining residuals show only the quiescent level and the flare itself. We show such a flare light curve in Figure 7.
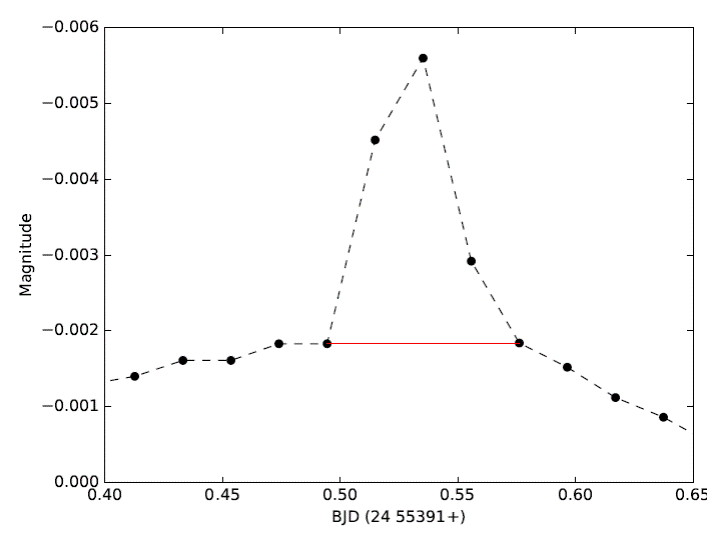
Fig. 7 An example of a flare light curve. The filled black circles represent the observations, while the red line represents the quiescent level derived from the data out-of-flare. The color figure can be viewed online.
The energy (E) is a very important parameter for a flare. However, the energy parameter has the luminosity L of the star as a factor in equation E = P × L described by Gershberg (1972). Due to the disadvantages described in Dal & Evren (2010), we use the flare equivalent duration instead of the flare energy, which is more proper. We compute the equivalent durations of flares via the equation P = [(Iflare − I0)/I0]dt (Gershberg 1972), where P is the flare equivalent duration in seconds, I0 is the quiescent level intensity, and Iflare is the intensity observed at the moment of the flare. Considering the quiescent level, the times of flare beginning, flare maximum and flare end are determined, together with flare rise duration, flare decay duration and flare amplitude. We list all computed values in Table 6 for each of the 13 flares.
Table 6 The parameters calculated for each
| BJD (24 00000+) 55021.2171 | P (s) 11.4 | Tr (s) 1763 | Td (s) 15889 | Amp (mag) -0.001516 |
|---|---|---|---|---|
| 55043.1016 | 5.6 | 1763 | 5296 | -0.002483 |
| 55310.6569 | 7.6 | 1763 | 8830 | -0.002047 |
| 55326.5140 | 2.7 | 1771 | 1763 | -0.001618 |
| 55412.0302 | 5.9 | 1763 | 7068 | -0.001648 |
| 55416.9343 | 12.1 | 1771 | 14118 | -0.002853 |
| 55824.2162 | 4.3 | 1763 | 5296 | -0.001578 |
| 55931.1213 | 4.5 | 3534 | 3534 | -0.001453 |
| 55971.7021 | 4.9 | 1763 | 5296 | -0.002152 |
| 56142.9809 | 6.0 | 3534 | 7059 | -0.001983 |
| 56284.8887 | 3.4 | 1771 | 3525 | -0.001806 |
| 56286.5642 | 4.4 | 1771 | 3525 | -0.001568 |
| 56375.4705 | 2.2 | 1763 | 1763 | -0.001429 |
Dal & Evren (2010, 2011) suggest that the best function to represent the relation between flare equivalent duration and flare total duration is the OPEA, where the flare equivalent duration is considered on a logarithmic scale. The OPEA function is defined as y = y0 +(Plateau−y0)×(1−e−kx), where y is the flare equivalent duration on a logarithmic scale, x is the flare total duration, and y0 is the flare equivalent duration in the logarithmic scale for the least total duration, according to the definition of Dal & Evren (2010). It should be noted that the y0 does not depend only on the flare mechanism, but also depends on the sensitivity of the optical system used in the mission. The most important parameter in the model is the Plateau value, which defines the upper limit for the flare equivalent duration on a logarithmic scale and is defined as the saturation level for a star (Dal & Evren 2011). Using the least squares method, the OPEA model leads to the results in Table 7. We plot the resulting model in Figure 8 with its 95% statistical sensitivity limit.
Table 7 Parameters derived from the OPEA
| Parameter | Value |
|---|---|
| Y0 | −0.015961±0.13891 |
| Plateau | 1.2394±0.14441 |
| K | 0.00011438±0.000036715 |
| Half-time | 6060 |
| R2 | 0.94535 |
| P value | ∼0.10 |
*Using the least squares method.
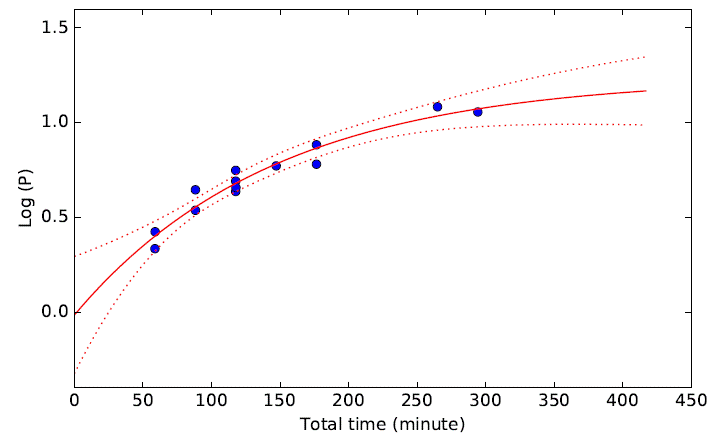
Fig. 8 The OPEA model obtained over 13 flares. The blue filled circles show each flare while the continuous red line shows the OPEA model and the dotted red lines show the sensitivity range of the model. The color figure can be viewed online.
We tested the derived model by using method proposed by D’Agostino & Stephens (1986) to understand whether there are any other functions to model the distribution of flare equivalent durations on this plane. In this method, the probability value (P value), is found to be ≈ 0.10, which means that there is no other function to model the distributions (Motulsky 2007; Spanier & Oldham 1987).
Ishida et al. (1991) described a frequency for the stellar flare activity as N1 = Σnf /ΣTt, where Σnf is the total flare number detected in the observations, while ΣTt is the total observing duration from the beginning of the observing season to the end. In the case of KIC9451096 we find the N1 frequency as 0.000368411 h-1 adopting the total long cadence observing duration as 1470.2786 days from the times of the first and last long cadence data points.
4. Summary and discussion
Photometric and spectroscopic analysis of KIC9451096 reveals that the system is composed of an F5V primary and a K2V secondary star in a circular orbit with a detached binary configuration. Medium resolution TFOSC spectra suggest that the system has one third of the [Fe/H] of the Sun. Light curve modelling reasonably represents the observations. However, we are able to catch the signals of additional light variation, which is very weak compared to the variations due to the binarity and eclipses, but still observable due to the very high precision of the Kepler photometry.
We observe occasional flares and rotational modulation of the light curve residuals from the eclipsing binary model. Considering the physical and atmospheric properties of the components, we attribute these variations to the secondary component, which is a perfect candidate for magnetic star spot activity with its deep convective zone owing to its spectral type and very fast rotation caused by short orbital period. We inspect rotational modulations of the residuals to trace the photometric period of the secondary component, and analyze its flare characteristics.
Photometric period analysis via O − C diagrams shows that the average photometric period is shorter than the orbital period by ≈ 0.5% day. Under any type of differential rotation assumption (either solar like, or anti-solar like), this means that the orbital period does not correspond to the equatorial rotation period of the star. Following the method proposed by Hall & Busby (1990), we find an average differential rotation coefficient of k = 0.069 ± 0.008, suggesting ≈ 3 times weaker differential rotation compared to the solar value of 0.19. We note that the type of differential rotation cannot be determined from photometry alone and we implicitly assume a solar type differential rotation in the case of KIC 9451096. However, the k = 0.069 value, which is extracted from very high precision continuous photometry for a restricted time range (four years in our case), defines a lower limit for the strength of the differential rotation of the star. A quick comparison of k values for other stars can be done by looking at the 17 stars listed in Hall & Busby (1990), where k values are usually a few percent or less, except for BY Dra with k = 0.17.
A more reliable way of detecting differential rotation with its magnitude and type is Doppler imaging, which is based on high resolution time series spectroscopy. Considering other stars whose k values were determined by Doppler imaging, we see mostly weak differential rotation with a k value of a few percent, both among solar type differential rotators (HD 208472 k = 0.015 (özdarcan et al. 2016), XXTri k = 0.016 (Künstler et al. 2015), ζ And k = 0.055 (Kövári et al. 2012), KUPeg k = 0.04 (Kövári et al. 2016)) and among anti-solar type differential rotators (UZLib k = −0.004 (Vida et al. 2007), σ Gem k = −0.04 (Kövári et al. 2015), HU Vir k = −0.029 (Harutyunyan et al. 2016)). Due to the binary nature of KIC 9451096, a considerable effect of tidal forces on the redistribution of the angular momentum in the convective envelope of the components can be expected, which would alter the magnitude of differential rotation (Scharlemann 1982). Based on observational findings, Collier Cameron (2007) suggests suppression of differential rotation by tidal locking, which is possibly in progress for KIC 9451096.
We detect 13 flares in the residuals from long cadence data, which are attributed to the secondary component with a corresponding B − V value of 0m.92 (Gray 2005). We apply the OPEA model to analyze flare characteristic and find that the calculated flare parameters and resulting OPEA model parameters seem to be in agreement with parameters derived from stars analogous to the secondary component, except for the half-time value. A possible source of disagreement for the half-time value is that there are not enough sample flares at the beginning of the OPEA model.
We find an N1 value of 0.000368411 h-1 for KIC9451096. N1 was found to be 0.41632 h-1 for KIC09641031 (Yolda ̧s & Dal 2016), 0.01351 h-1 for KIC 09761199 (Yolda ̧s & Dal 2017), and 0.02726 h-1 for Group 1 and 0.01977 h-1 for Group 2 of KIC 2557430 (Kamil & Dal 2017). Among these systems, KIC9451096 has the lowest N1 value, which indicates that the magnetic activity level of the secondary component of KIC 9451096 is the lowest, according to Dal & Evren (2011).
We thank TüBI ̇TAK for partial support in using RTT150 (Russian-Turkish 1.5-m telescope in Antalya) with project number 14BRTT150-667. This paper includes data collected by the Kepler mission. Funding for the Kepler mission is provided by the NASA Science Mission Directorate.











 nueva página del texto (beta)
nueva página del texto (beta)





