1. INTRODUCTION
The performance of any optical/infrared (O/IR) telescope is determined by its point spread function (PSF). For perfect, circular optics this characteristic is entirely determined by just one parameter: the aperture diameter, which in turn determines the exact shape of the PSF for a particular observing wavelength.
In reality there are some other factors, related to environmental conditions and constructive specifics of the telescope, which may have a strong influence on its final PSF. For a ground-based telescope the most influential external factor is the atmospheric optical turbulence, which leads to image blur in the telescope’s focal plane. The quantitative criterion for assessing the quality of optical turbulence is so called seeing, which represents the full-width at half maximum (FWHM) angular size of the atmospheric long-exposure PSF. In the absence of other adverse factors (telescope tracking, vibration, focusing, etc.) the ultimate shape of the telescope’s PSF is determined by the pure optic PSF and the seeing.
Usually, circular apertures are assumed, when assessing the potential abilities of different size telescopes. But actually all modern medium to large size O/IR telescopes have annular apertures (except for solar telescopes) due to central obscuration, dictated by the optical and mechanical design. This affects the characteristics of the perfect optics in a few ways: firstly it simply blocks incoming light by the amount corresponding to respective detail’s size, thereby reducing the aperture effective area; secondly it alters the shape of the PSF; and thirdly it contaminates the focal plane by the light scattering and diffractive effects on the respective elements (baffles, spiders etc) (Kuhn & Hawley 1999). For pure annular apertures the parameter ε = d/D is used to describe the order of central obscuration. Here d and D are, respectively, the inner and outer diameters of the annulus. In some cases the obscuration can be relatively big and may significantly change the PSF characteristics. This is especially the case for survey telescopes where ε can reach 0.4 0.6. Typical examples of different class instruments are the Pan−Starrs (D = 1.8 m, ε ≈ 0.57), SDSS (D = 2.5m, ε ≈ 0.52), VISTA (D = 4.1m, ε ≈ 0.41) and LSST (D = 8.4 m, ε ≈ 0.61). In such cases the final (telescope + seeing) PSF may also be changed noticeably and hence the optical power of the telescope.
In this paper I consider the influence of central obscuration on the final performance characteristics of a telescope, while working under certain seeing condition. Here pure annular apertures without any spider are assumed. A brief summary of parameters and formulas is presented in § 2. The results of the analysis are given in § 3 followed by the discussion and conclusions in § 4.
2. THEORETICAL BASIS
The main optical characteristic is the point spread function (PSF). It represents the normalized intensity I of the point like source as function of coordinates in the focal plane. For a perfect annular aperture with obscuration ε it can be presented mathematically as (Born & Wolf 1970):
where k = 2π/λ is the wave number, λ is the observing wavelength, a is the aperture radius and
Another important characteristic of any optical system is the optical transfer function (OTF), H(u, v). Mathematically the PSF and OTF are Fourier transforms of each other:
where u and υ are spatial frequencies. The modulus of the OTF, called modulation transfer function (MTF), represents the ability of the optical system to transfer different spatial frequencies. For ideal optics with an annular aperture the OTF Hopt(f) can be represented by:
Where
otherwise;
and the spatial frequencies
Ground-based O/IR telescopes are subjected to the adverse influence of the atmospheric optical turbulence. In essence the terrestrial atmosphere is a randomly changing optical system in front of the telescope which can be characterized by its own parameters. With the use of atmospheric optical turbulence theory (Tatarskii 1961) it is possible to describe this system. The coherence radius or Fried parameter, r0 is the main characteristic of the atmospheric optical turbulence condition, defined by Fried (1965) as
where z is the zenith angle, and
The seeing, β represents the FWHM angular size of the atmospheric optical turbulence long-exposure PSF
The angular resolution, θ0 represents the FWHM size of the telescope’s ultimate (optics + atmosphere) PSF.
It has been shown (Fried 1966) that the long exposure OTF of the atmosphere is
where Dφ is the phase structure function and for Kolmogorov turbulence it is represented by
where r0 is normalized to the aperture size D.
For the case of a finite turbulence outer scale L0, it can be described as (Jenkins 1998)
where K is a Bessel function of the second kind and L0 is also normalized to the aperture size D.
The ultimate OTF of the telescope is a product of pure optics Hopt and atmospheric Hturb OTFs
3. RESULTS OF NUMERICAL ANALYSIS
3.1. Infinite Outer Scale
3.1.1. Angular Resolution
The FWHMs are calculated by using the above mentioned formulas. At first, the OTFs of a telescope for a particular ε and atmosphere for a certain r0 are calculated. Then the final PSFs are determined via the Fourier transform of the ultimate OTFs. The corresponding FWHMs are normalized to the unobstructed (ε = 0) case. The results are presented in Figure 1. Here for convenience the horizontal axis indicates a D/r0 relation. It can be seen that D/r0 ≳ 1.1 the FWHMs of obscured apertures are relatively wider and have local maxima at D/r0 ≈ 2.2. This corresponds to a wavefront overall rms error of σφ ≈ 1.97 rad. But for D/r0 ≲ 1.1 the angular resolution of an obscured aperture becomes higher. The figure also indicates that when σϕ ≲1 rad diffraction effects dominate over the optical turbulence in a process of long-exposure PSF formation.
3.1.2. Integral Contrast
Integral contrast (IC) is defined as the integral of the telescope’s ultimate MTF over the entire spatial frequencies:
This definition is more appropriate as a performance metric, which concerns the spatial resolution when dealing with extended objects. It can be used to characterize quantitatively the ability of a telescope to reproduce the fine structure of an object. In order to make a comparative analysis relative values ICε/ICε=0 for different obscuration parameters are calculated (Figure 2). It is seen that the relative IC curves have local minima at D/r0 ≈ 1.25 i.e. when σφ ≈ 1.22 rad the relative performance of an obscured telescope is significantly worse than it would be without the presence of optical turbulence.
3.1.3. Signal-to-Noise Ratio
It is well known that the signal-to-noise (S/N) ratio of a point-like source with an intensity B notably less than sky background level b is given by:
where q is the detector’s quantum efficiency (noise contribution is neglected), τ is the system’s overall transmittance and t is the exposure time. Under equal conditions, a certain “image size” dε has to be found in order to achieve maximal S/N for a particular PSF. For a comparative analysis relative S/N values for a certain ε normalized to unobstructed case are calculated by:
where I0,
Iε, are the final
(telescope + atmosphere) PSFs and
d0,
dε are the optimal
“image sizes” for circular (ε = 0) and annular apertures,
respectively. The results are presented in Figure 3. In these calculations the coefficient
3.2. Finite Outer Scale
The turbulence outer scale adds its own contribution to the telescope’s final performance. As
it follows from expression (9) accounting for L0 leads to a smaller wavefront
phase error under the same seeing. Unlike the previous case, where performance
characteristics can be introduced as a function of only one parameter
(D/r0 or wavefront overall
error as
It can be seen that the introduction of L0 notably changes the relative performance curves (Figure 4). Particularly, the local maxima/minima for all characteristics are shifted towards bigger D/r0 values while L0/D is decreasing. At the same time maximum points for FWHMs become relatively higher, whereas minimum points for contrast and S/N become less deep. The final relative performance characteristics of the assumed telescope are presented in Figure 5.
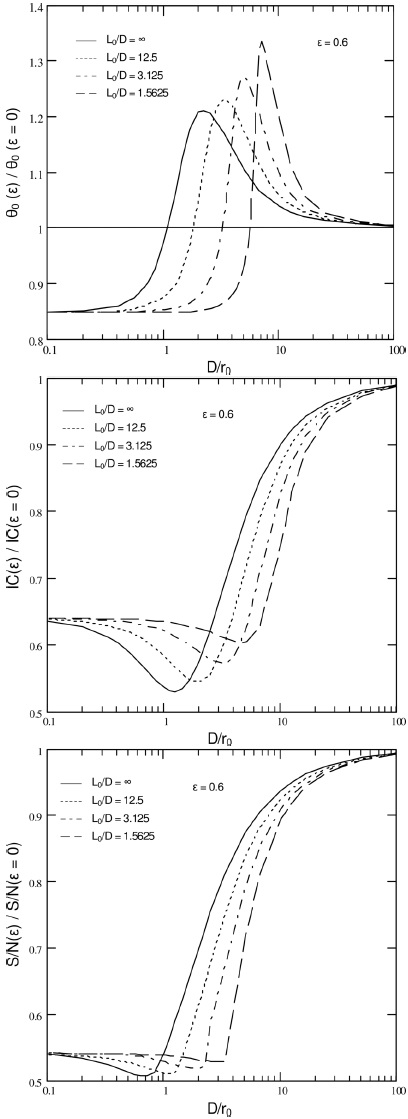
Fig. 4 Relative FWHM, IC and S/N (influence of the effective area reduction is subtracted) curves evolution for ε = 0.6 and L0/D = ∞, 12.5, 3.125, 1.5625.
4. DISCUSSION AND CONCLUSIONS
Ground-based O/IR telescopes with annular pupils acting under certain optical turbulence condition have performance characteristics which differ from those of circular ones. This difference is not constant, as for the seeing-free case, but apart from the obscuration parameter ε it also depends on the seeing β, the turbulence outer scale L0 and the observation wavelength λ.
If a Kolmogorov power spectrum is assumed then the telescope relative performance for different obscuration can be presented as function of D/r0. In the case of finite outer scale L0 the situation is complicated and each case with certain L0/D must be considered separately.
The general trend of the performance curves is that FWHMs and IC values for D/r0 ≫ 10 are nearly the same as for an unobstructed telescope. At the same time, relative S/N values are smaller initially due to the aperture’s effective area reduction. As the D/r0 relation decreases the characteristics decline, reach a certain extremum point and then rise gradually up to the levels corresponding to the seeing-free case (D/r0 ≪ 1). The interesting result is that at certain values of D/r0 the relative performance of an obscured telescope becomes worse. The extrema correspond to D/r0 ≈ 2.2, 1.25, 0.67 for the resolution, IC and S/N respectively. For instance, under a 0.8′′ seeing the maximum effect on the resolution will occur for telescopes with D ≈ 0.31, 1.64 and 4.2 m for the V, K and M-band respectively. So in this condition the effect in the visible is strongest for small-size telescopes but in the NIR to mid-IR medium-size telescopes are most severely affected. Performance degradation can be as much as ≈ 21%, 47% and 49% for the resolution, IC and S/N (after accounting for vignetting) respectively, for ε = 0.6.
The presence of a finite outer scale, L0, shifts the extrema towards bigger D/r0 values. As the L0/D relation decreases the angular resolution at the extremal point continuously deteriorates up to ≈ 34% for L0/D = 1.5625 and ε = 0.6. (Figure 4). Meanwhile, the IC and S/N become slightly less degraded. For instance, under a 0.8” seeing and L0 = 25 m, maximum deterioration of resolution for telescopes with D=2,4 and 8m will be at λ≈1.84, 2.9 and 4.16 μm respectively.
It is seen that the most severe performance deterioration of any medium to large size (D ≳ 2m) telescope, working in the seeing-limited mode, takes place in the NIR to mid-IR spectral bands. But the situation will dramatically change if, for example, adaptive optics (AO) methods are applied. It can be shown (Martinez et al. 2010) that low-order AO implementation is equivalent to a reduction of the initial outer scale to the smaller “effective” L0 size and a simple tip-tilt compensation will lead to an “effective” L0/D of ~ 2. For this condition the extreme points will be at D/r0 ~ 6.5, 4.5, 2.9 for the FWHM, IC and S/N respectively (Figure 4). In this observational mode, under a 0.8′′ seeing, the maximum effect on resolution will be for apertures with D ≈ 0.91, 4.8 and 12.3 m for the V, K and M-band. Furthermore, the AO compensation for higher order aberration terms will reduce “effective” L0 futher to significantly smaller values. So in this observational mode the effect of a central obscuration for large size apertures may become significant even in the optical bands.
A relative performance analysis is done for an 8 m aperture with ε = 0.6 in analogy to modern large size survey telescopes. It turns out that the relative performance of such a telescope, working in the seeing limited mode under the adopted atmospheric conditions can significantly differ from an unobstructed aperture of the same size. In general the angular resolution, θ0 can be relatively better or poorer depending on the observation band and the turbulence parameters, whereas the IC and S/N are always degraded. If we assume L0 = 25 m as a more probable value then performance degradation appears to be at levels less than ≈ 6% in the V -band for all suggested seeing conditions. The maximum effect occurs in the K to M-bands. Particularly, θ0 can be decreased by up to ≈ 34% or increased by up to 15% depending on the seeing. At the same time, for example, the angular resolution at the M-band may be superior or inferior to the unobstructed case under the same β = 0.8′′ seeing depending on the outer scale L0 size (Figure 5). Contrast also gradually decreases from ≈ 0.99 in the U-band (300 nm) to nearly 0.57 in the NIR. S/N is the most affected characteristic, which drops from 0.8 to 0.41 from the U-band to the M-band respectively. So losses of penetrating ability may reach 0.95m in some spectral bands.
Modern telescopes are indeed sophisticated optical-mechanical systems which are dedicated to
solve different scientific tasks. So the ultimate choice of the telescope’s optical
scheme is a trade-off between complex technical issues and performance requirements.
Usually the central intensity ratio (CIR) (Dierickx
1992) is used for a ground-based telescope’s performance evaluation. It
represents the IC drop caused by pure optical imperfections, relative to perfect
case and CIR ≥ 0.82 is widely adopted as a requirement. Now if we generalize this
criterion on the topic which is being considered, then the maximum affordable
obscuration will be determined. So the requirement on CIR leads to corresponding
requirements on
ICε/ICε
= 0 ≥ 0.82. It turns out that the obscuration parameter must
be ε < 0.34 in order to satisfy the above mentioned precondition
through a broad spectral region. At the same time CIR also indicates the peak
intensity drop in a telescope’s actual long-exposure PSF relative to the perfect
case and
Actually, many modern telescopes have obscurations which exceed these values. As it follows from calculations, losses of optical power may be significant in a certain spectral region. For medium to large size telescopes, acting in the seeing-limited mode, this region mainly falls in the NIR to midIR part of the spectrum. But if an AO technique is applied then the situation will change. In particular ground-layer AO (GLAO) or multi-object AO (MOAO) techniques allow to partially compensate for wavefront errors in a relatively large field. So the “equivalent seeing” will become notably better and will push the extreme region toward shorter wavelengths. So it makes sense to seriously consider such classes of telescopes with off-axis optical design schemes, which will allow to more efficiently realize their potential capabilities.











 nueva página del texto (beta)
nueva página del texto (beta)






