1 Introduction
In recent years, the investigation and analysis of small celestial bodies have become fundamental to deep space exploration. Thus, understanding the dynamical behavior in the vicinity of small bodies is of great interest for the design of exploration missions and also for planetary science.
However, describing how a particle behaves around these objects is a challenging subject in astrodynamics, mainly due to the combination of the rapid rotation of the asteroids around their axis together with the non-spherical shapes.
In particular, an increasing number of binary asteroid systems has been observed throughout the Solar System and, in particular, among the near-Earth asteroids (NEAs). It is estimated that about 15% of NEAs larger than 0.3 km are binary systems Pravec et al.(2006), Margot et al.(2015). Most of these binaries are formed by a more massive primary component, usually with a nearly spherical shape, and a small secondary component, generally referred to as satellite Pravec et al.(2006), Pravec & Harris(2007), Walsh et al.(2008), Zhang et al.(2020).
There are several types of binary asteroid systems, which have been grouped according
to their physical properties (e.g. size, rotation, mass ratio, diameter; Pravec & Harris 2007). The characteristics
of these groups also suggest different formation mechanisms. As shown by Pravec & Harris(2007), the Type A binary
asteroids are composed of small NEAs, Mars crossers (MC), and Main-Belt Asteroids
(MBA), with primary components less than 10 km in diameter and with a component size
ratio (
Most Type A binary asteroids are synchronous systems, that is, the rotation period of the secondary component is equal to the orbital period around the center of mass of the system Pravec et al.(2006), Pravec et al.(2016). Numerical simulations revealed that binary systems are likely to undergo a chaotic process of energy dissipation involving tidal forces that allows the system to evolve to a fully synchronous end state Jacobson & Scheeres(2011). According to Jacobson & Scheeres(2011), the higher the mass ratio of the binary system, the faster the synchronization can be achieved. This happens because each member of the system exerts tidal forces with the same proportion over each other. Thus, as most systems have mass ratios less than 0.5, we find in the literature a larger number of systems with only the secondary component coupled with the orbital movement Pravec et al.(2016).
Performing semi-analytical and/or numerical investigations of the orbits and equilibrium solutions around asteroid systems using simplified models can be useful to provide some preliminary understanding of such systems Werner(1994), Liu et al.(2011). Simplified models can be used to approximate the gravitational field of irregularly shaped bodies, requiring less computational effort and generating considerable results in a short period of time. Another advantage of using a simplified model is that we can easily investigate the effects of a given parameter on the dynamics of a spacecraft around asteroids, such as, the distribution of stable periodic orbits Lan et al.(2017), the stability of the equilibrium points Zeng et al.(2015), Barbosa Torres dos Santos et al.(2017), as well as the permissible parking regions Yang et al.(2015), Zeng et al.(2016). In addition, simplified models can be used to support the orbit design Wang et al.(2017) and feedback control Yang et al.(2017).
Due to their advantage and considerable results, several simplified models have been
proposed to study the orbital dynamics of a particle in the vicinity of irregular
bodies. For example, Riaguas et al.(1999),
Riaguas et al.(2001) analyzed the
dynamics of a particle under the gravitational force of an asteroid modeled as a
straight segment. Zeng et al.(2016) analyzed
the influence of the parameters k (angular velocity) and
In particular, aiming to understand the dynamical environment in the vicinity of irregular bodies, Aljbaae et al.(2020) investigated the dynamics of a spacecraft around the asynchronous equal-mass binary asteroid (90) Antiope; the authors applied the Mascon gravity framework using the shaped polyhedral source Chanut et al.(2015), Aljbaae et al.(2017) to consider the perturbation due to the polyhedral shape of the components. The perturbations of the solar radiation pressure at the perihelion and aphelion distances of the asteroid from the Sun were also considered in that study. In order to investigate the stability of periodic orbits, Chappaz Howell(2015) considered the asynchronous binary asteroid system using the triaxial ellipsoid model and observed that the non-spherical shape of the secondary body significantly influences the behavior of the halo orbit around L 1 and L 2 .
As said before, simplified models are useful to provide some preliminary understanding of the motion around binary systems, and the circular restricted three-body problem is suitable and often used to investigate the dynamics around small bodies de Almeida Junior Prado (2022). Furthermore, even landing trajectories have been evaluated using a spherical shape for the gravitational field of the primaries in the circular restricted three-body problem Tardivel Scheeres (2013), Celik Sanchez (2017), Ferrari et al. (2016). Although the orbit-attitude coupled equations of motion for a binary asteroid can be obtained using a more sophisticated model, which takes into consideration a potential for a non-spherical distribution of mass Scheeres et al.(2021), Wen Zeng (2022), they are only essential for very close encounters, such as for landing approaches. In this study, the dynamics is investigated for orbits around the binary system of asteroids. Thus, in this contribution, a more simplified model is used, whose results capture the essential parts of the physics of the problem, although its accuracy depends on the parameters of the specific mission. Therefore, we carry out a numerical investigation using the simplified model called a Restricted Synchronous Three-Body Problem, as introduced by Barbosa Torres dos Santos (2017). The practical advantage of using this model is that we can, in a relatively simple way, analyze the influence of the dimension of the secondary body on the dynamics of a spacecraft in the neighborhood of M 2.
We focus on the behavior of a particle of negligible mass in the vicinity of a binary
system of Type A (NEAs and MBAs). The reason for choosing this class of asteroids is
that the NEAs, in particular, are asteroids that pass near the Earth and most of the
systems that are part of this class are synchronous systems. Our aim is to
understand how the parameters of the dipole, the dimension (d) and
the mass ratio (
2 Equations of motion
Consider that the motion of a particle with negligible mass,
In canonical units, the sum of the masses of the bodies M
1 and M
2 is unitary. In this work, for all numerical simulations, we assume that
The angular velocity, given by
With respect to the barycentric rotating frame, the masses m
1, m
21 and m
22 are fixed along the x-axis with coordinates
Using the generalized potential
we can write the equations of motion of P in a rotating frame centered on the barycenter of the system (M 1- M 2) as follows:
with
where
The free parameters of the system are d,
2.1 Equilibrium Point and Stability Analysis
Let
The equilibrium points L
i
, i = 1,2,3,4,5 are defined as the zeros of
where
To determine the linear stability of the equilibrium points (L
i
, i = 1,2,3,4 and 5), it is necessary to transfer the
origin of the coordinate system to the position of the equilibrium points
where the partial derivatives in
In equations 5 - 7,
where
where c3 and c4 are integration constants.
When the motion is in the xy plane, the non-trivial characteristic roots of the
equations 5, 6 were obtained in Barbosa Torres
dos Santos et al.(2017) (considering k = 1.). The linearization
around L1 and L2 provides a pair of real eigenvalues
(saddle), corresponding to one-dimensional stable and unstable manifolds, and
one pair of imaginary eigenvalues, suggesting a two-dimensional central subspace
in the plane xy, which accounts for an oscillatory behavior around the
equilibrium point of the linear system Howell(1982), Haapala et
al.(2015). Hence, in general, for L1 and L2,
the stability type is
Consider the linearized dynamics around the L1 equilibrium point. We
will adopt the coordinates
Due to the fact that these initial conditions were chosen to nullify the unstable and stable eigenvectors, they provide a harmonic movement in the linear system.
Now that we have the initial conditions for the linear system, we want to find a periodic planar orbit in the nonlinear system.
We note that the potential function for the system studied here depends only on
the distances that a spacecraft are from the primary bodies, that is, it has
symmetry with respect to the x-axis. Taking advantage of the fact that the
planar orbits are symmetrical with respect to the x -axis, the initial state
vector takes the form
3 Collinear equilibrium points as a function of the ratio between gravitational and centrifugal accelerations
In this section, we analyze the influence of the parameter k on the position of the
collinear equilibrium points, since the influence of d and
To determine how k affects the positions of the collinear equilibrium points, we
consider
Figure 2 shows the x coordinates of L1, L2 and L3 as a function of k. Because they are at both ends of the x axis, the positions of L2 (right curve) and L3 (left curve) are more affected than the position of L1. Consider that there are three forces acting on the system: (i) the gravitational force of M1; (ii) the gravitational attraction of M2; and (iii) the centrifugal force, which is directly proportional to the angular velocity of the system around the center of mass and the distance between the equilibrium point and the center of mass of the system. Thus, by decreasing the angular velocity of the asteroid system around the center of mass, as k becomes larger, it is necessary to increase the distance between P and the center of mass, such that the centrifugal force remains at the same value and it counterbalances the gravitational forces from M1 and M2, which remain unchanged. Thus, L2 and L3 move away from the center of mass of the system. Although L1 also moves away from the center of mass of the system, it does so in a more subtle way. This is because, when moving away from the center of mass of the system, L1 approaches M2. Regarding the gravitational force increases, a balancing force is needed to prevent L1 from going too close to M2.
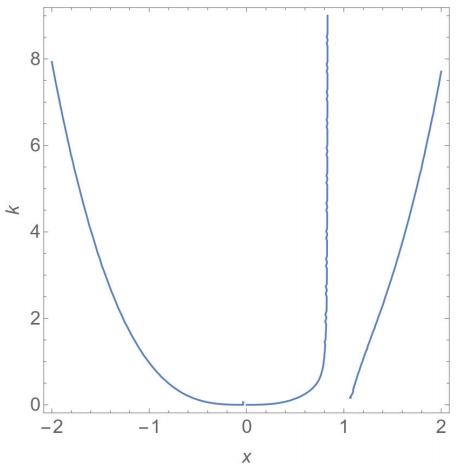
Figure 2: x-coordinates of the equilibrium points L1, L2 and L3 for different values of k. The color figure can be viewed online.
As shown in Figure 2, the x coordinates of
L2 and L3 tend to
4 Periodic orbits around the first and second collinear equilibrium points as a function of the mass parameter and the size of the dipole
Based on previous knowledge about Type A asteroids, we consider that the most massive
primary is spherical in shape and with a diameter of 5 km Pravec Harris(2007), Walsh
Jacobson(2015). Also, knowing that, on average, the mutual orbit of type
A binary asteroids has a semi-major axis of about 4.8 primary component radii Walsh & Jacobson(2015), we consider that
the distance between the bodies is 12 km, which is the normalization factor for the
distances. Finally, type A asteroids are known to have moderately sized secondaries,
ranging from 4% to 58% of the size of the primary; the mass ratios
Periodic orbits are of special interest to explore the dynamical behavior of a massless particle in the vicinity of two primary bodies.
The results below were obtained by calculating approximately 3500 orbits from each family, starting from an initial condition with very low amplitude, and continuing the families until the orbits obtained came near the surface of the asteroids. To find symmetric periodic orbits, we consider k = 1, that is, the bodies orbit the center of mass of the system without any internal forces.
Each family was calculated for different values of
We are interested in the stability of the periodic solutions, which can be determined
by analyzing the eigenvalues of the monodromy matrix. Given the sympletic nature of
the dynamical system, if
The stability indices offer a useful measure of orbital stability. Following Broucke (1969), the stability index is defined
as
Given that the periodic orbits growing from the collinear points inherit the
stability properties of L1, L2, and L3, the
eigenvalues of the monodromy matrix of these orbits and corresponding stability
indices appear as: (i) a trivial pair of unitary values, resulting in
4.1 Planar Orbits
Figure 3 shows a family of planar orbits
around L1 with
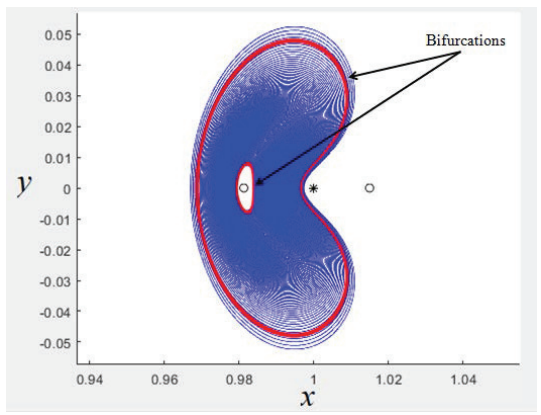
Figure 3: Planar orbits around of the equilibrium point L1
considering
In Figure 3, the red orbits indicate where bifurcations occur, that is, when one of the stability indices s1 or s2 reaches the critical value 2. Note in Figure 3 that the maximum position reached by the infinitesimal mass body in the x component, when the second bifurcation occurs, is greater than the position of the secondary body.
Although many bifurcations exist in dynamical systems, only two types of bifurcation are of particular interest for the focus of this work; the pitchfork and period-multiplying bifurcations.
A family of periodic orbits undergoes a pitchfork bifurcation when the stability
of the periodic orbit changes as a parameter evolves, which in our case is the
energy constant. During this type of local bifurcation, a pair of eigenvalues
(non-trivial) of the monodromy matrix pass through the critical values
When building the families of planar orbits, with d = 0 and
For
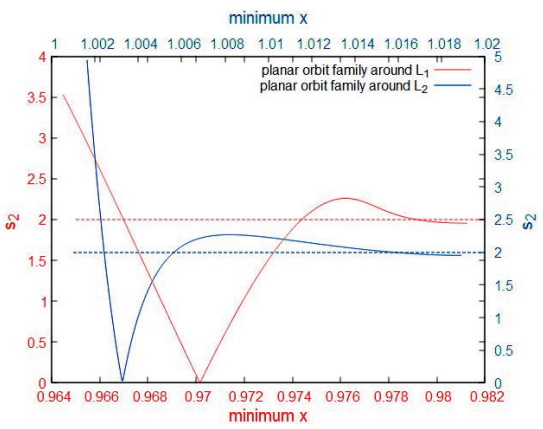
Figure 4: Stability index (s2) around L1 (red) and
L2 (green) considering d = 0 and
Figures 5 (a), (b) and (c) provide
information about the types of the bifurcations that occur along the family of
planar orbits. For
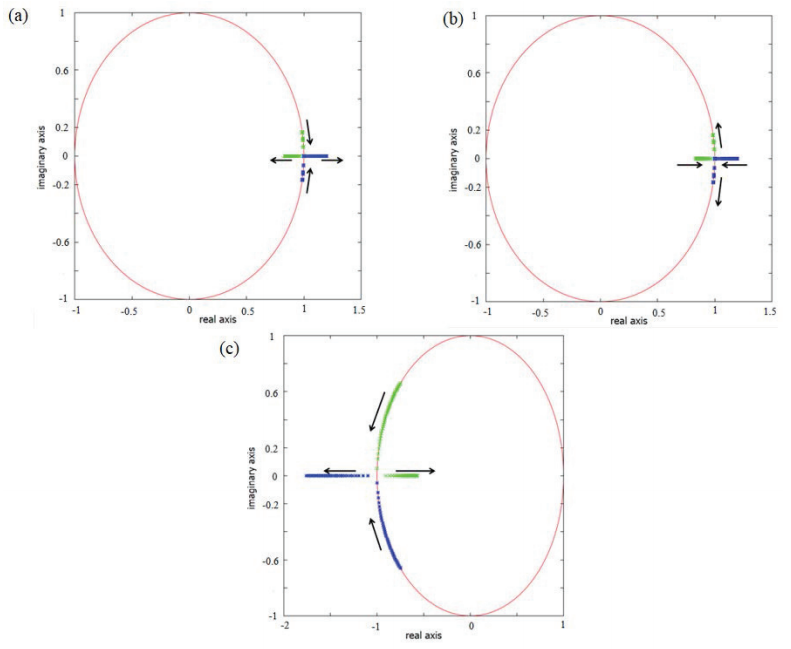
Figure 5: (a) Behavior of the characteristic multipliers at the first
pithckfork bifurcation around L1 and L2. (b)
Behavior of the characteristic multipliers at the second pithckfork
bifurcation around L1 and L2. (c) Behavior of
the characteristic multipliers that leads to the period-doubling
bifurcation around L1 and L2. In these cases
we consider d = 0 and
Figure 5 (c) shows the behavior of the eigenvalues at the third bifurcation. The characteristic multipliers start in the imaginary plane and move until they collide on the negative real axis and start to reach only real values on the negative axis. Thus, the eigenvalues indicate a period-doubling bifurcation.
Figure 6 and 7 provides information about the stability index (considering the
values of s2), around L1 and L2, respectively,
when we increase the dipole dimension from 0 meters, that is, the body is
modeled as a mass point, up to the dimension of 2000 meters. In this analysis we
consider the constant mass ratio in the value of
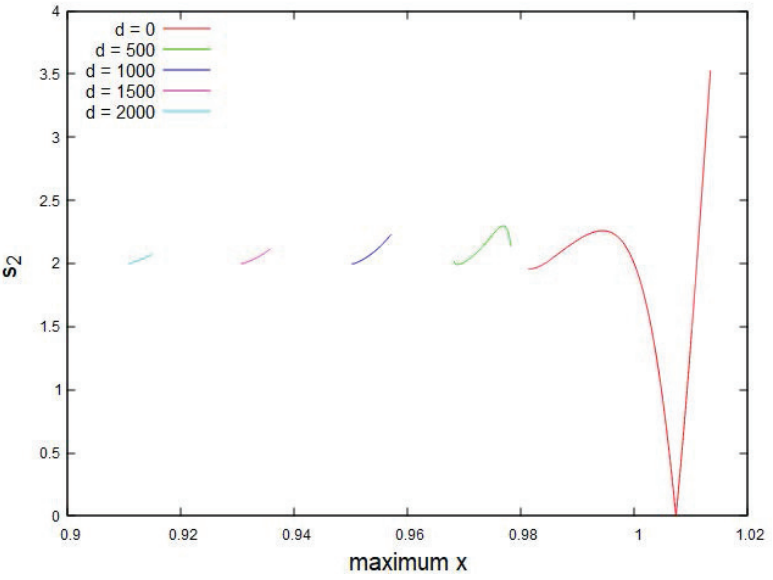
Figure 6: Planar orbit stability index around L1 for different values of d. The color figure can be viewed online.
4.2 Influence of the Mass Parameter and the Size of the Dipole on the Planar Orbits
Now, we investigate how the planar orbits evolve as a function of the dipole size and mass ratio in canonical units. With the normalization factor being D = 12000 meters, the dipole sizes used in our study were d = 0, 500, 1000, 1500 and 2000 meters.
Figures 8 provide information about the
stability index s1 of the planar orbits around L1,
respectively, as a function of d and
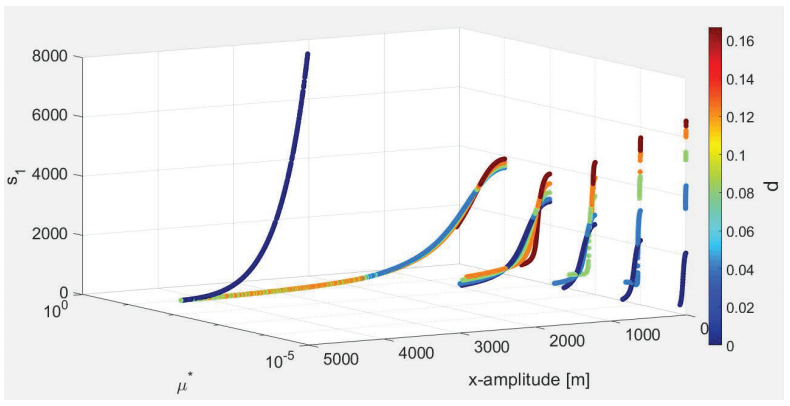
Figure 8: Stability index (s1) of the planar orbits around
L1 for different values of d and
First, we investigate the solutions as d varies and
If we consider d = 0, which corresponds to the CRTBP, we observe that as
Next, we analyze the period of the planar orbits in terms of d and
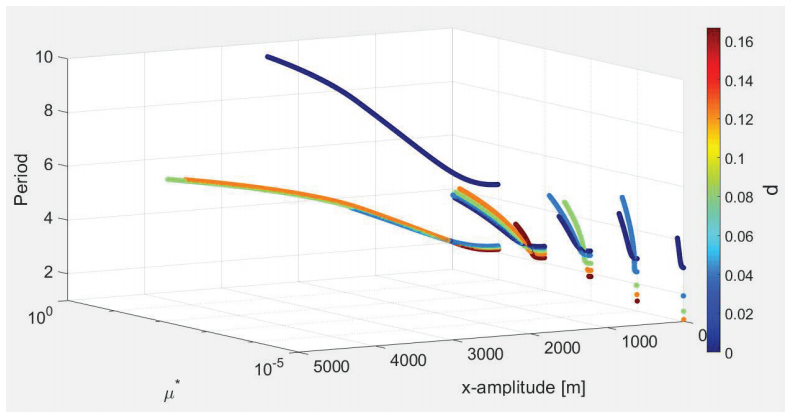
Figure 9: Period of planar orbits around L1 for different values
of d and
Considering the family with d = 0, when
Finally, we analyze the energy of the system in terms of d and
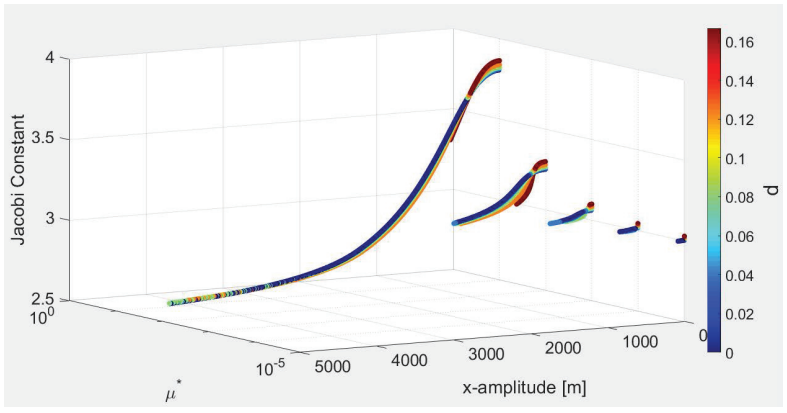
Figure 10: Jacobi constant of planar orbits around L1 for
different values of d and
We find that when d or
4.3 Computing Halo Orbits
Halo orbits are a three-dimensional branch of planar orbits that appear when the
planar orbit stability index reaches the critical value s2 = 2. Figure 11 shows a family of halo orbits
around L1 with
Figure 11: Halo orbits around the L1 equilibrium point
considering
To find the initial conditions of the halo orbit, we keep the coordinate
x0 fixed and search for
with
The differential is
where
All the information we need to start Newton’s method is shown above.
From the cylinder theorem, it was possible to find a halo orbit family. Thus, having found a halo orbit and noticing that it has exactly two unit eigenvalues, we can use that as a starting point to move along the cylinder. We use the initial conditions from the previous halo orbit as a starting point to find the next halo orbit at a slightly larger value of x (x coordinate closer to the secondary asteroid). If we find another halo orbit here, we iterate through the process. In this way it was possible to calculate a halo orbit family. The x coordinate step to determine each halo orbit was x = 0.00002.
4.4 Halo Orbits
Figures 12 and 13 illustrate how the halo orbits appear at the tangent
bifurcations of the planar orbits around L1 and L2 when
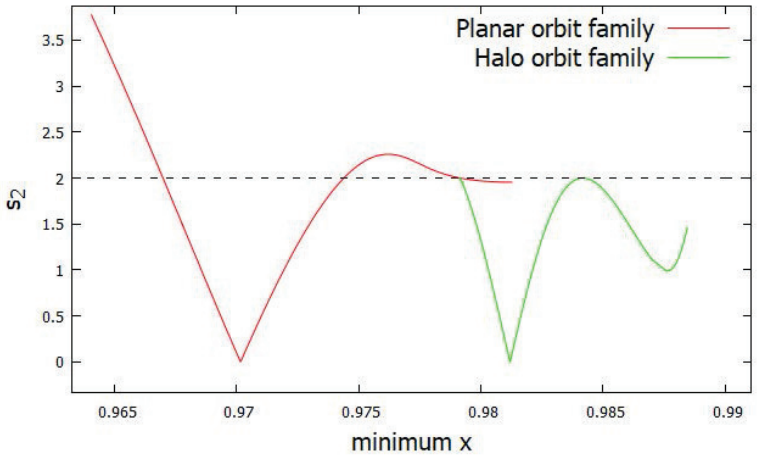
Figure 12: Stability index (s2) of the planar and halo orbit
families around L1 considering d = 0 and
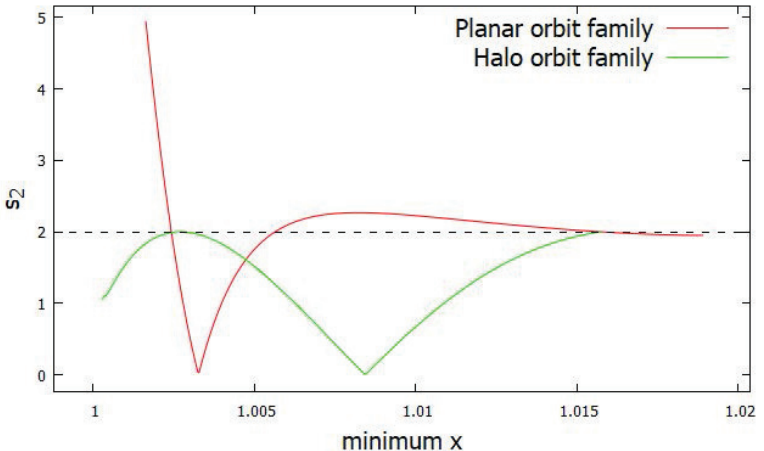
Figure 13: Stability index (s2) of the planar and halo orbit
families around L2 considering d = 0 and
For the conditions considered here, the halo orbit appears at x
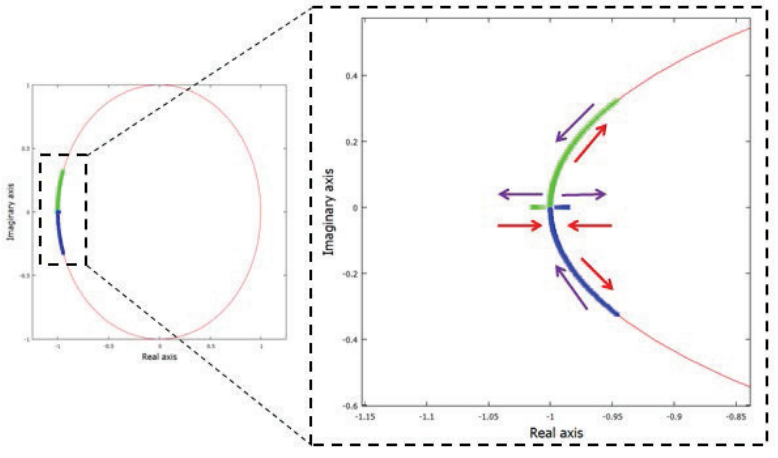
Figure 14: Behavior of the of characteristic multipliers at the period doubling bifurcation. The color figure can be viewed online.
Figures 15 and 16 provide information about the s1 stability
index as a function of d and
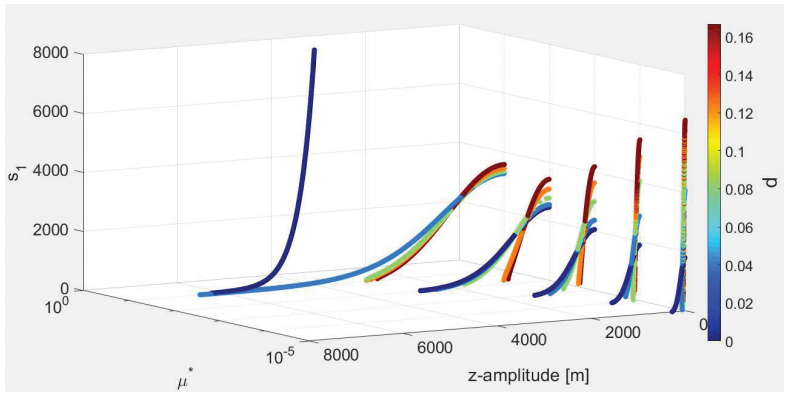
Figure 15: Stability index (s1) of halo orbits around
L1 as a function of d and
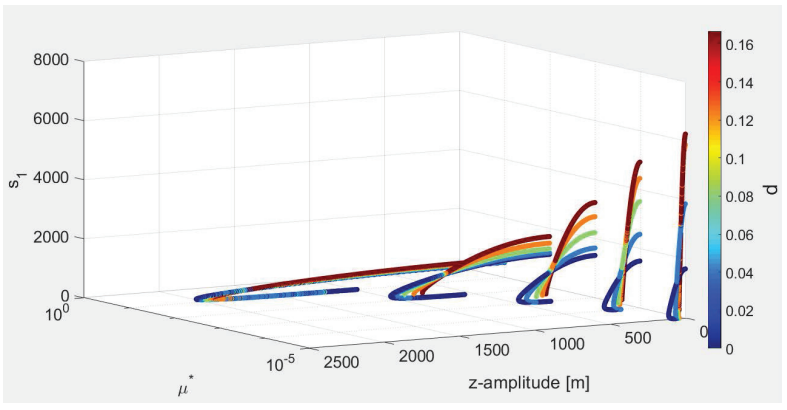
Figure 16: Stability index (s1) of halo orbits around
L2 as a function of d and
Figures 17 and 18 provide information about the stability index
s1 as the size of the dipole increases from 0 to 2000 meters and
the mass ratio is kept constant at
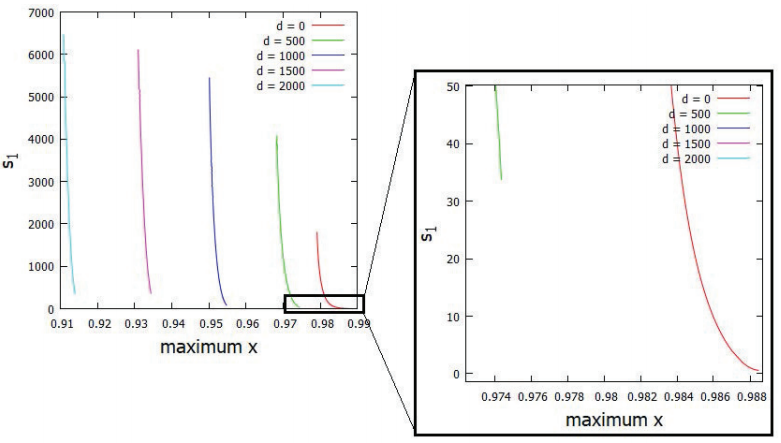
Figure 17: Halo orbit stability index around L1 for different values of d. The color figure can be viewed online.
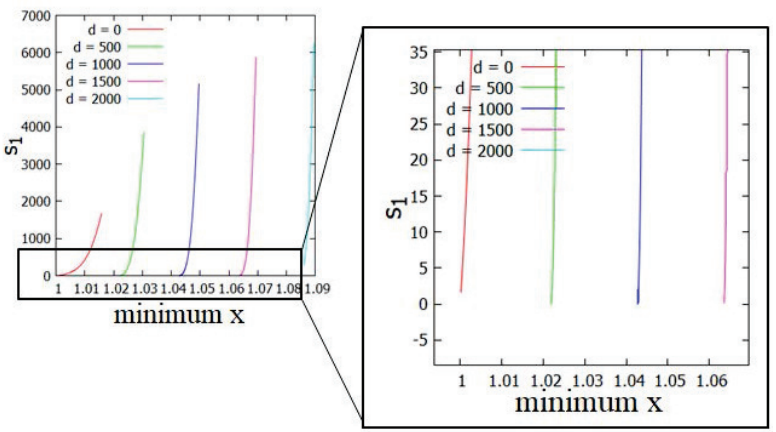
Figure 18: Halo orbit stability index around L2 for different values of d. The color figure can be viewed online.
Note that it is unlikely to detect NRHOs around L1 when we take into
account the elongated shape of the secondary body and assume small values of
However, as shown in Howell(1982), the
stability index also depends on the mass ratio of the system. Considering d = 0
and increasing
Now we analyze how the period of the halo orbits around L1 and
L2 is affected by d and
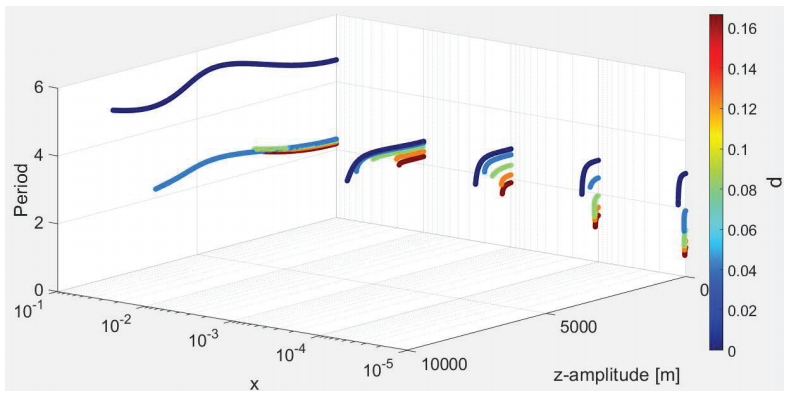
Figure 19: Period of the halo orbits around L1 as a function of d and μ*. The color figure can be viewed online.
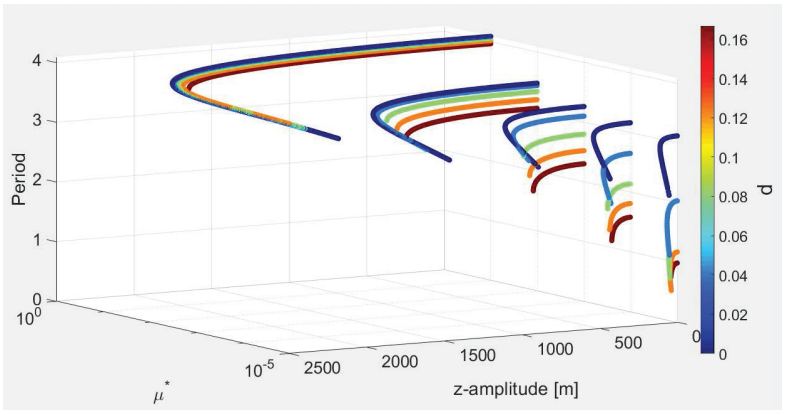
Figure 20: Period of the halo orbits around L2 as a function of d
and
This is because the gravitational attraction is stronger near the particle, due to the mass distribution of the secondary body, causing the acceleration to increase and the orbital period to decrease. As the amplitude of the halo orbit increases, its orbital period becomes shorter.
Considering the elongated shape of the asteroid, but keeping d constant and
increasing
Figures 21 and 22 provide information on the behavior of the Jacobi
constant of the halo orbits as a function of d and
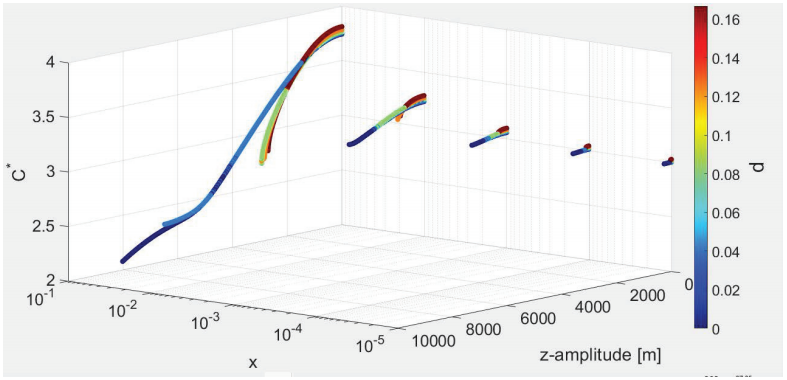
Figure 21: Jacobi constant of the halo orbits around L1 with
respect to d and
5 Conclusion
In this paper, the general dynamical environment in the vicinity of binary asteroid systems is explored. Based on the physical and orbital parameters of type A asteroids, the positions of the collinear balance points as a function of angular velocity were computed. We found that the locations of the collinear equilibrium points L3 and L2 are more sensitive to changes in the rotation rate, compared to L1.
Families of planar and halo orbits were computed around these equilibrium points and we found that the closer the periodic orbits are to the equilibrium point, the more unstable they are.
Numerical evidence shows that the stability of the periodic orbits around the
equilibrium points depends on the size of the secondary body and on the mass ratio
of the system. We observed that, the more elongated the secondary body, the more
unstable the planar orbits are. Additionally, we detected unstable and stable halo
orbits when d = 0 and when
Finally, we observed that, keeping the mass ratio constant, the more elongated the secondary body, the lower the orbital periods of planar and halo orbits around the equilibrium points.
Thus, if a spacecraft were to be placed in the vicinity of an equilibrium point, fuel consumption required for orbital maintenance would be higher around more elongated secondary bodies.











 nueva página del texto (beta)
nueva página del texto (beta)





