1. Introduction

This paper deals with the problem of jointly smoothing output and unemployment rates. The problem can be approached from several standpoints, e.g., by considering a single or a multiple time-series setting. Here, we concentrate on a bivariate time series approach that assumes that the observed time series vector is composed of an unobserved vector of trends plus a vector of cycles, and that takes into account the correlation between output and unemployment cycles. In the macroeconomic literature of real business cycle theory employed here, the cycle of output is usually called the output gap, since it corresponds to the difference between potential output, i.e., the underlying trend of output, and actual output. ^{Laxton and Tetlow (1992)} provided a historical overview of estimation procedures of potential output and found that basically two approaches had been employed since the 1980s: (1) structural approaches that rely on a structural economic model, as in ^{Ford and Rose (1989)} and ^{Adams and Coe (1990)}; and (2) stochastic approaches such as that underlying the ^{Hodrick and Prescott (HP, 1997)} filter.

^{Laxton and Tetlow (1992)} combined those two approaches and proposed a semi-structural technique which is called the Hodrick-Prescott Multivariate filter (HPMV). ^{Boone (2000)} and ^{Chagny and Lemoine (2002)} apply this approach in their works. However, the HPMV is not a true multivariate filter, but a multiple time series filter. This difference is akin to that of a multiple regression where there is only one dependent variable to be explained by several independent ones, while multivariate regression considers several dependent variables to be explained simultaneously by one or more independent variables.

We propose a different semi-structural technique that is based on a true multivariate time series filtering method that we call a Bivariate Hodrick-Prescott filter (BHP), in order to decompose the time series vector into trend plus cycle, taking into account the correlation between cycles of the two series. Our basic aim is to estimate the cost of unemployment in terms of potential output according to Okun’s Law. An approach similar to ours is that of ^{Dermoune, Djehiche and Rahmania (2009)} except for the fact that we emphasize the smoothness of the trend, which is the most important feature of a time series trend. We can measure the smoothness and control it by fixing the value of a smoothing parameter, in order to obtain comparable results for the different series considered by the vector of variables under study.

In his seminal paper, ^{Okun (1962)} estimated that a 1-percentage-point increase in unemployment would induce a decline in output growth of about 3.3 percent. We want to stress that the underlying assumption for measuring the impact of unemployment on potential output is that the unemployment rate summarizes -or is correlated with- other variables such as: average hours worked, participation rates and labor productivity. In other words, unemployment “...can be viewed as a proxy variable for all the ways in which output is affected by idle resources...” (^{Okun, 1962: 2}). This assumption is very important for obtaining and predicting a fixed coefficient between unemployment change and output growth; otherwise, one should not expect this coefficient to be fixed. Furthermore, it implies that technological advances, changes in labor market institutions, variations in participation rates and demographic shifts, among other things, would induce changes in the coefficient.

The literature on this topic identifies three different techniques for estimating Okun’s coefficient: (i) by means of a simple two-step procedure; (ii) as part of a bivariate trend-cycle model for output and unemployment; and (iii) by assuming that the coefficient varies over time. The conventional method for estimating Okun’s coefficient involves a two-step procedure: First the permanent component of the output and unemployment series is estimated and removed and then the correlation between the transitory components is estimated. The permanent component of the series can be obtained using techniques that range from estimating the trend component by Ordinary Least Squares (OLS) to using the HP filter. In some cases, the permanent component is simply eliminated by taking first differences of the series. When the series is stationary this first step is omitted. Once the permanent component has been estimated, the transitory component is obtained by subtracting the estimated permanent component from the observed series. In the second step Okun’s coefficient is estimated by OLS.

^{Sinclair (2009)} claims that the above methodology provides a biased and inefficient coefficient estimate for two reasons. First, since the permanent and transitory components of the two series are correlated, it is more efficient to estimate their cyclical components jointly. Second, to the extent that the measurement error of the independent variable is correlated with the measurement error of the dependent variable, OLS estimates are biased and inconsistent. Thus, a better approach uses the estimate of the correlation rather than the correlation of the estimates.

A second technique, proposed by ^{Clark (1987)}, takes this criticism into account and involves the use of a bivariate model to jointly estimate the permanent and transitory elements of unemployment and output. Such an approach was proposed as a reaction to ^{Nelson and Plosser’s (1982)} methodology to remove non-stationarity by first differencing, assuming that the trend behaves as a random walk with drift rather than as a deterministic straight line. In fact, ^{Clark (1987)} pointed out that two shortcomings of this approach are, first, tests for non-stationarity in trend have very little power against plausible alternatives; second, the analysis is based on the strong assumption that the auto-covariance function for the first difference of output is exactly zero after lag one. Thus, he proposed a new method for analyzing United States output and unemployment data by decomposing each series into a non-stationary trend and a stationary cyclical component. The framework for his analysis is a state-space model that allows for a fairly general specification of the trend component.

A few years later, ^{Clark (1989)} used Kalman filtering and Maximum Likelihood to estimate the non-stationary permanent and stationary cyclical components of output growth and unemployment for six developed economies (Canada, France, Germany, Japan, United Kingdom and United States), and found strong evidence that the estimated output’s stationary component is closely related to unemployment’s cyclical component. ^{Evans (1989)} used a bivariate Vector Autoregressive (VAR) model to describe the output-unemployment dynamics, to estimate the degree of persistence in output innovations, and to decompose output into trend and cycle. He concluded that the bivariate analysis indicated the existence of feedback, as well as a negative contemporaneous correlation between output growth and unemployment innovations.

The third estimation technique was developed because there is some empirical evidence that the coefficient has not remained constant over time. In fact, since the mid-1990s, an increasing number of studies have investigated whether Okun’s coefficient is stable over time. For example, ^{Prachowny (1993)} argued that the 3:1 ratio of output to unemployment holds only because other factors, including weekly hours worked, induced a tendency for labor supply and productivity to rise as well. An important conclusion of Prachowny’s paper is that if any of the other factors change then, other things being equal, the coefficient linking output to unemployment will change as well.

In this paper we do not seek to compare the previous approaches, which are mentioned just for completeness but, as mentioned before, we aim to estimate the unobserved trend and cycle components of output and unemployment, as well as Okun’s coefficient, simultaneously. To do that, we propose the use of a BHP filter that arises as a simple extension of the original Penalized Least Squares (PLS) problem that gave rise to the HP filter. As such, the BHP filter provides a straightforward solution to the estimation problem, without requiring a full statistical model specification with its corresponding assumptions, but just the existence of second order moments.

Thus, our proposal is in line with the aforementioned second type of techniques, but we employ a new way of calibrating the smoothing parameter involved, that basically consists of fixing a desired percentage of smoothness to be achieved by both the output and unemployment trend estimates. This is the approach followed by ^{Guerrero (2008)} in a univariate time series setting; by doing so we obtain comparable trends that are estimated jointly with the correlation coefficient between cycles. The results obtained in the empirical application to United States data are seen to be sensible and resemble those produced by a complete structural model specification, with the advantage that our results are obtained with relative ease and do not require validating model assumptions, since no statistical model specification is employed, but only a filtering technique. Thus, our approach emphasizes the idea of simplicity over a complete model specification.

The organization of the rest of this article is as follows. Section 2 shows the derivation of the BHP filter and its solution by means of a state-space representation. In section 3 we illustrate the use of the proposed BHP filter with a real application to United States data on real GDP and unemployment. A comparison of our results is made with those obtained previously by ^{Sinclair (2009)}. In section 4 we conclude with some final remarks.

2. Statistical Methodology

Let us define a bivariate column vector Z_t = (Z_1t , Z_2t)´ where prime denotes the transpose of that vector throughout this paper. We assume that the bivariate time series under study is given by the signal-plus-noise model

Where Z_t is the observed vector, tau_t is also a bivariate vector denoting its trend (signal) and η _t is the bivariate vector denoting its cycle (noise). Of course, as in the univariate case, such a representation does not correspond with the data generation process, but it basically serves to capture the stylized facts and allows us to use very simple tools to estimate the trend with a desired percentage of smoothness, as indicated below.

We are concerned here with the estimation of the trend component given the sample of observations {Z_t } for f or t = 1, . . . , N and means of PLS as did ^{Guerrero (2008)} in the univariate case. To do that we consider the problem of minimizing the following quadratic function

With lambda > 0 a smoothing constant that penalizes the lack of trend smoothness and W a known symmetric and positive definite matrix of constant weights. Thus, for all t and i = 1, 2, if we let λ → 0 both trends approach the observed data, i.e., τ_i,t → Z_i,t, and when λ → ∞, τ_i,t −2τ_i,t−1 + τ_i,t−2 → 0, so that every element of τ_t tends to behave like a straight line. Now, the smoothness of a trend depends only on its length (N ), the value of the smoothing parameter (λ) and the correlation between cycles, as can be seen in the smoothness index (10) presented below. Note that only one smoothing constant is used to smooth both trends -unemployment and growth- since at the present situation both time series: (i) have the same length and (ii) share the same amount of smoothness.

Note also that there are some slight differences among different authors in the treatment of endpoints when using the HP filter. Some authors take the second summation similar to (2) to be over t = 3 to N , while others take the summation over t = 2 to N −1, or some others take it over t = 1 to N . There is no clear preference. We chose to follow ^{Guerrero’s (2007)} bivariate expression. This author addressed the end-of-sample problem within a PLS setting by centering the differenced trend series about a nonzero mean µ. The effect of including this parameter is to get a better fit of the trend at both ends of the original series, thus improving the forecasting ability of the trend. We do not include such a mean here because our interest in the present work is not to forecast the bivariate trend but to estimate Okun’s coefficient. If we consider the stacked vectors Z=Z1´,…,ZN´´ and τ=τ1´,…,τN´´ the problem can be posed as that of minimizing

where I_N is the N-dimensional identity matrix, ⊗ denotes Kronecker product and K is an (N − 2) × N matrix representing the second order difference operator, that is,

The solution to the minimization of (3) is provided by ^{Guerrero, Islas and Ramirez (2017, GIR from here on)}, that is

This solution provides the same numerical results as those obtained by Kalman filtering with smoothing, as shown by ^{Gómez (1999)} in the univariate case. It should be stressed that (5) is valid when both λ and W are known. Thus, the practical problem lies in providing adequate values for those parameters. GIR solved this problem by applying Generalized Least Squares (GLS) on the assumption that the smooth trend behavior is described by

and making W=∑η-1and λI2=∑ε-1 with ∑_n, the symmetric variance-covariance matrix of covariance matrix of η_t and ∑_ε that is the diagonal variancecovariance matrix of ε_t, that is

Then, the variance-covariance matrix of the GLS estimate is given by

where Σ_η and Σ_ε are assumed to be known. GIR showed that the correlation between trends may be taken into account by using a nondiagonal matrix Σ_ε, whose effect is practically irrelevant for trend estimation. In fact, this article showed that even correlations as high as 0.95 produce an increment in smoothness from 80% to slightly over 83% for sample sizes between 100 and 400, which covers the sample size considered in this paper.

3. Empirical application

The dataset used in this application is the same one used by ^{Sinclair (2009)}.¹ It contains quarterly data on real GDP in logs, Z_y,t , and civilian unemployment rate, Z_y,t , from 1948:1 up to 2005:4. Sinclair employed a theoretical bivariate correlated unobserved-component model and we have now the opportunity to contrast the results from that study with those produced by the BHP filter in terms of estimated components of output and unemployment, as well as the Okun’s coefficient obtained by that study. We carried out all computations with the WinRATS package, version 8.10 (http://www.estima.com).

First of all, we followed the guidelines in GIR who recommend to visually appreciate the behavior of the two series under study; since in this case one of the series follows essentially a straight line (GDP in logs) and the other one does not behave as a straight line (unemployment), GIR’s recommendation led us to the decision of using 80% smoothness for this application. The correlation ρ_ηyηu = −0.6 was suggested by step b) of the estimating algorithm (see the Appendix) so that the smoothing constant corresponding to 80% smoothness for the trend with N = 232, was obtained from Table A in the Appendix and became λ = 16.29. On the other hand, Table 1 reports the esti-mates of the variance-covariance matrix Σ_n and ρ_{ηyη u} obtained from step c) of the estimating algorithm, while Figures 1 and 2 show the estimated trend components of real GDP in logs and unemployment rate respectively, along with two-standard error limits derived from

Figure 1 U.S. unemployment and estimated components, 1948:1 2005:4 

Figure 2 U.S. real GDP and estimated components, 1948:1 2005:4 

We should stress that 80% smoothness was decided on by following suggestions for choosing appropriate percentages of smoothness in GIR, which depend on the type of behavior of the time series under study, as visually appreciated in time series plots. These suggestions include asking for high percentages of smoothness, say above 85%, when both trends follow a straight-line pattern. When one trend is linear and the other is nonlinear, the percentage of smoothness should diminish to between 80% and 85%; and when both trends are nonlinear it is reasonable to ask for lower amounts of smoothness, say below 80%. GIR concluded that the estimated trends with these choices resemble the “true” trends of the simulation reasonably well.

The two estimated trend components were produced by the Kalman filter with a smoother that uses all information available in the sample, thus providing a better “in-sample” fit as compared with the basic Kalman filter without smoothing. The cycle components, obtained by subtracting the corresponding trends from the observed series are plotted at the top of Figures 1 and 2, together with those obtained by ^{Sinclair (2009)}, where the shading in those figures represents NBER recession dates.

As in ^{Sinclair (2009)}, the estimated permanent components of GDP and unemployment are not as smooth as those obtained within the framework of business cycle theory. In fact, the estimated perma-nent component of GDP looks slightly more variable than the series itself. This result is similar to that obtained by the Beveridge-Nelson decomposition of GDP series and in ^{Morley, Nelson, and Zivot (2003)}; but it is contrary to ^{Clark (1989)} which separately decomposes output and unemployment into trend and stationary components. He used the covariance between the stationary components of the two series to support his case for the existence of large temporary movements in real output.

^{Clark (1989)} found evidence that the correlation between the permanent and transitory components of GDP is statistically non-significant. On the other hand, when the components of GDP and unemployment are jointly estimated with no restriction on the covariances, as in ^{Sinclair (2009)}, the results are significantly different from ^{Clark (1989)}, and provide further support of a small cyclical component for GDP. Even more, as suggested by ^{Dupasquier, Guay and St-Amant (1999)}, if the model includes the dynamics of permanent shocks in potential output, the size of the output gap would be extremely small.

A closer examination of Figures 1 and 2 indicates not only that the transitory shocks of our estimates display comparable magnitudes with respect to the ones obtained by ^{Sinclair (2009)}, but also that the turning points in our estimates indicate a little more clearly the phases of the economic cycle. The turning points in Sinclair seem to be delayed by two periods because of the Auto-Regressive structure of order 2 in the model employed. In Figure 3, a close-up of the 1981, 1990 and 2001 recessions, we can observe, as in ^{Sinclair (2009)}, that the estimated permanent component dips well below the series in all three recessions. This implies a positive transitory component, since the series is above its steady state value, therefore our results differ from theories that describe recessions as temporary negative movements.

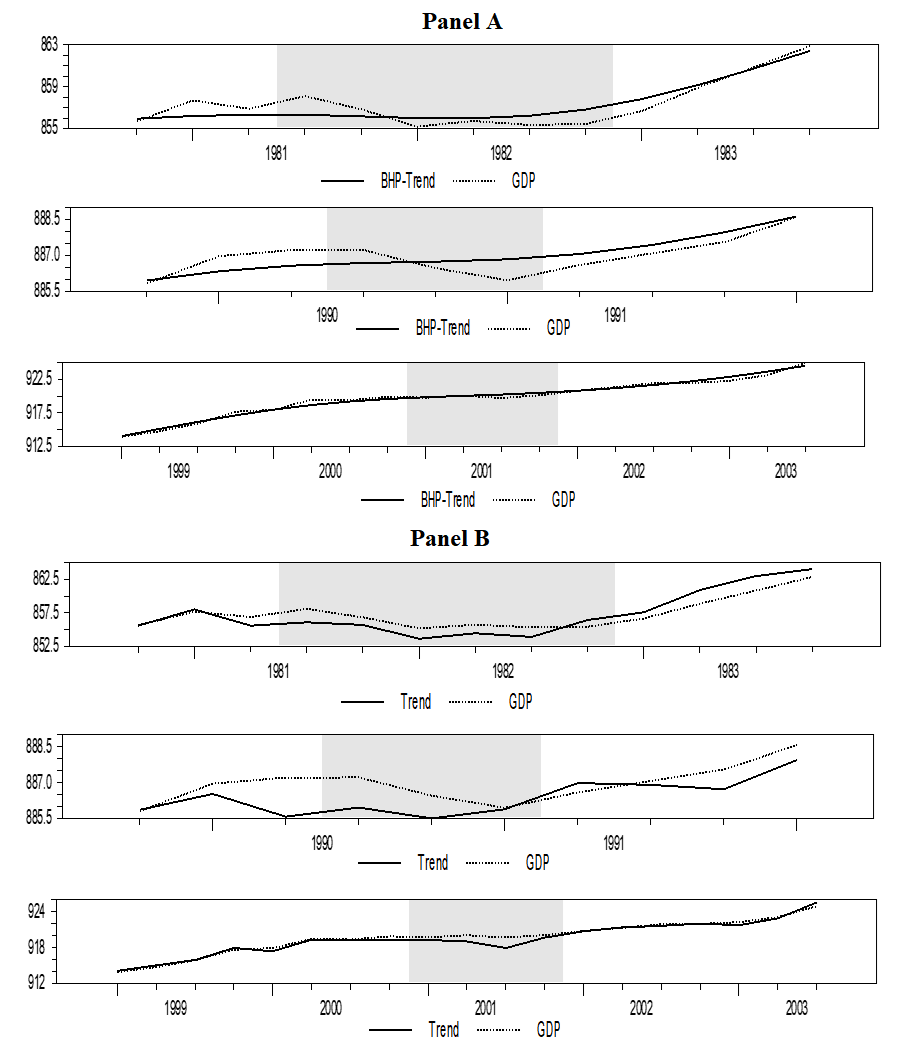
Figure 3 Close-up of the 1981, 1990 and 2001 recessions Panel A: BHP’s results, Panel B: ^{Sinclair (2009)} results 

Regarding the permanent component of unemployment, as we found with GDP, a sizable amount of movement in the unemployment rate appears to arise from permanent shocks. A closer examination of Figure 1 shows a positive permanent movement in unemployment, rather than the temporary movements that some theories of recession would predict. Similar to Sinclair’s proposed model, the BHP filter also provides new estimates of the relative importance of permanent versus transitory movements in the unemployment rate.

Many models have previously treated unemployment as stationary, including ^{Blanchard and Quah (1989)}, who identify supply disturbances as those that have a permanent effect on output, and demand disturbances as those that have no permanent effect on out-put. These authors find a tight relation for demand disturbances, but supply disturbances present a confusing picture. Some authors (e.g.^{Sinclair, 2009}) have explained that this is due to the fact that their models don’t allow for a permanent stochastic component to unemployment. Furthermore, Blanchard and Quah’s assumption that all movements in unemployment are temporary drives the finding of a much large transitory component.

The results of ^{Blanchard and Quah (1989)}, and ^{Clark (1989)} are appealing because the estimated transitory components appear to follow the NBER business cycle. In particular, the transitory component of GDP in Clark is similar to the cycle obtained when a deterministic linear trend is used to represent the permanent component of GDP. Even though both of these transitory components match those found in textbooks, they are rejected by the data when less restrictive models are used, as in ^{Sinclair (2009)} and GIR. As discussed by ^{Nelson (1988)}, it appears that the estimates of the transitory component are actually spurious cycles, not the properly estimated transitory component. We want to point out that the methodology used in this paper was tested through simulation to avoid this error, and our results show that more complex model specifications, even though they may seem more appropriate, may not yield better results than those produced here.

The results presented in this work support those of ^{Sinclair, 2009}, and, likewise, call into question a number of macroeconomic theories for the post-war US. In particular, studying permanent movements separately from transitory movements in GDP or unemployment implicitly requires the assumption that they are uncorrelated. Further-more, “...theories explaining only growth (permanent movements) or only transitory movements cannot provide adequate macroeconomic insights if there are important interactions between the two...”^{Stock and Watson (1988: 148)}. Therefore, the results of this paper, as well as those of Sinclair, cast doubt on models that study GDP growth and transitory movements separately, as well as on models that treat business cycle movements as exclusively temporary, and theories such as the often-called models of hysteresis, where some part of the temporary shock persists and becomes permanent. On the other hand, our results are in line with real business cycle theories such as the one presented by ^{Kydland and Prescott (1982)} and ^{Prescott (1987)}, where transitory movements in the series arise primarily from adjustments to permanent changes.

Okun’s law, given by Equation (14), suggests that the transitory components of output and unemployment rate are negatively correlated. This finding is relevant to answering the following question: given a certain level of unemployment, what level of GDP should one expect under the economic conditions prevailing during the sample period? To answer this question, we estimated Okun’s coefficient by means of Equation (15) and obtained θ = −0.3462/0.1893 = −1.82, implying that a 1 percentage-point decrease in transitory unemployment corresponds to a 1.82 percentage-point increase in transitory real GDP. Even though both our estimate and that of ^{Sinclair (2009)}, -1.4, are below the 2% consensus estimate (e.g.^{Grant, 2002}), ours is closer and both are within the range of usual estimates, which varies between 3% (^{Okun, 1962}) and 0.67% (^{Prachowny, 1993}).

We then compare Okun’s coefficient estimated using the BHP filter with the estimate obtained through the conventional two-step procedure; in the first step, the permanent components of the output and unemployment series were estimated separately using the univariate HP filter with the smoothing parameter set to 1600, as is standard for quarterly data. This λ value produces a smoother trend than the one suggested by our proposal (λ = 16.29). This smoother trend incorrectly includes permanent movements in the transitory components of GDP and unemployment that lead to an upward bias in the estimation of Okun’s coefficient in the second step, which applies OLS to (14) and takes on the value θ = −1.9.

Figure 4 allows us to appreciate the results of the HP filter as compared with those produced by the BHP filter and ^{Sinclair (2009)}. We should be aware that the smoothness achieved varies according to the sample size. For instance, the smoothness achieved by applying the HP filter to the GDP and the unemployment rate data with N= 232 and λ = 1600 is about 93.9%. Therefore, ignoring the correlation between noise components leads to smoother trends and more incorrect inclusion of persistent noise components.

Figure 4 Real GDP, the unemployment rate and the estimated components produced by the univariate HP filter with λ = 1600 

4. Conclusions

The suggested BHP filter is an easy-to-use tool that can be employed to estimate trends of bivariate time series with controlled smoothness, that is, when we want to establish (valid) comparisons between trends obtained with the same pre-specified percentage of smoothness. In addition, comparisons between the corresponding cycles are also valid. Of course, univariate time series filtering is even easier to apply but it may give misleading results since it does not take simultaneity in the estimation into account. On the other hand, we showed that some more complex model specifications, even though appropriate, may not yield better results than those produced by the BHP filter. Furthermore, we should keep in mind that the results produced by a filter do not rely heavily on statistical assumptions, and such assumptions, which are the basis for more complex theoretical models, must be validated with the data at hand.

In the empirical application shown here we found that the results obtained with the BHP filter reproduce the most important, and positive, features of a more complicated procedure based on a structural model and avoid a negative aspect related to the displacement of the cycle phases. Moreover, as compared with the univariate HP filter, we found that the BHP filter produces an estimate of the correlation coefficient that avoids the bias and inconsistency of the usual two-step procedure associated with the HP filter.