1. Introduction
Due to its high economic value, walnut cultivation has been steadily increasing across the world in recent years, with about 1.3 million ha and an average yield of 4.5 million t. Turkey ranks third in the world due to its annual walnut production of nearly 225 000 t (FAO, 2019). Walnut trees can easily adapt to various soil and climate conditions. Walnuts require cool enough weather in winter and autumn to satisfy the need for cooling and a temperature of 25-35 ºC in spring and summer, which is enough to support normal growth and maturing. Although it takes a long time to grow, walnut is one of the most widespread fruit species in the world, with a cooling requirement of 400-1800 h. In general, walnut trees adapt more easily to valleys that are sun-drenched in the summer and moderately warm in winter, protected from the wind. In certain regions, late frosts in the spring are among the most important factors which cause inefficiency in walnut trees.
Irrigation and the correct choice and application of the irrigation method are too among the most important factors. A total minimum annual precipitation of 500 mm is sufficient for walnut cultivation; however, it is of great importance that the precipitation is regular. Especially in the summer, there should be enough water and humidity in the soil. According to many studies that have examined crop yield response to irrigation of walnut trees, their annual water demand is around 750-1500 mm (Goldhamer et al., 1982, 1984; Fulton et al., 2003; Chauvin et al., 2005; FAO, 2012; Goldhamer and Beede, 2015). There are many studies about irrigation modernization, as well as various irrigation project designs (Fukui et al., 1980; Andrade and Allen, 1999; Ortega et al., 2004; Rocamora et al., 2013; Zapata et al., 2013). The topics of drip irrigation and the quality of irrigation water for good crop production were studied by Ayers and Wescott (1985), Grattan et al. (2004), Master et al. (2007), Díaz and Grattan (2009).
The estimation of walnut crop evapotranspiration (ET) is of great relevance for improved water management, especially in arid and semi-arid regions where irrigation is needed to stabilize and increase agricultural production. ET is a vital variable for hydrological and agrometeorological studies and, particularly, for the optimization of water use in agricultural crop cultivation. A particular attention is given to the estimation of crop evapotranspiration (ETc) in arid and semi-arid regions, under water scarcity, and when crops are exposed to different kinds of abiotic stress (water, salinity, etc.). However, modeling ETc is a complex process due to its non-linear structure and the intricate relationship between meteorological and crop parameters. Moreover, the measurements of crop ET are tedious and prone to errors due to difficulties in adequately considering numerous factors that affect the uniformity and stability of the soil-plant-atmosphere continuum (Allen et al., 2011). Consequently, the investigation of the most appropriate and accurate methodology for ET estimation remains a priority topic for the planning and management of water resources, on-farm irrigation scheduling, crop growth simulations, and climate change studies. There are different methods and techniques for measuring or estimating ET. Each of them has advantages and disadvantages based on their usage and data requirements. Many researchers have investigated the direct and indirect measurement of ET using lysimeters and other tools; however, this is a time consuming and expensive method (Campbell and Norman, 1998; Dinpashoh, 2006; Ali and Shui, 2009; Ding et al., 2010; Abyaneh et al., 2011; Aghajanloo et al., 2013; Jovanovic et al., 2018).
The Penman-Monteith (PM) equation is one of the most widely used methods to assess reference grass evapotranspiration (ETo) based on weather variables. It is recommended by the Food and Agriculture Organization (FAO) of the United Nations as a standard method (FAOPM) for ETo estimation (Allen et al., 1998). This method was tested against many other equations under different climatic conditions and for various time steps adopted for ET estimation (Todorovic, 2006; Pereira et al., 2015).
There are some alternative machine learning techniques that can be used for ET estimation as more economical and less time-consuming methodologies. However, these methods are difficult to develop due to the non-linear dynamic complexity of the ET process, which depends on the interaction of several meteorological and crop variables (Martí and Gasque, 2010; Traore et al., 2010). Moreover, the accuracy of ET estimation by mathematical approaches depends on the number of available meteorological parameters, as well as the quality of measured input data. Since the beginning of this century, machine learning algorithms have been increasingly applied in modeling ET (Kumar et al., 2002, 2011; Trajkovic et al., 2003; Pal and Deswal, 2009; Martí and Gasque, 2010; Kisi et al., 2015; Yassin et al., 2016; Mattar, 2018; Mehdizadeh, 2018; Sattari et al., 2020). Antonopoulos and Antonopoulos (2017) studied the estimation of daily ETo using artificial neural networks (ANN) and empirical methods in northern Greece. Their results demonstrated that the application of ANN yielded a satisfactory performance (Kisi, 2016; Dou and Yang, 2018). Tabari et al. (2013) studied the adaptive neuro-fuzzy inference system (ANFIS) and support vector machines (SVM) for modeling potato ETc in northwest Iran. The results demonstrated that the ANFIS and SVM techniques simulated better potato ETc than all empirical methods.
This study was aimed at identifying the best model to estimate crop-walnut ET based on scenarios including meteorological data and to compare it with a well-known and frequently used method.
2. Materials and methods
2.1 Study site
The study was performed in the walnut orchards in the district of Gölcük, Kocaeli, Western Turkey (40º 43’ 36.5” N 29º 48’ 23.8” E) as shown in Figure 1. All the orchards where walnuts were cultivated had been set up according to the cultivators’ own knowledge and experience. While some of the orchards were set up on the plain, others were set up on high lands within the forest, approximately 500-800 masl. The district is under the influence of the Black Sea climate, but it also exhibits the semi-arid climate properties of the Marmara region. When average climatic values measured throughout many years (1950-2015) are studied, it is seen that the average temperature is 23.8 ºC, while the highest average temperature has been measured in July as 29.6 ºC. The lowest average temperature has been measured in January as 3.3 ºC. The average number of rainy days has a maximum of 17.4 in January and a minimum of 5.2 in August. The annual average rainfall in the region is 768 mm. Total monthly precipitation has been recorded to be highest in December, with an average of 110.0 kg m-2, and lowest in July, with an average of 37.1 kg m-2 (TSMS, 2017). The four-year climate data of the region used in the models were obtained from the General Directorate of Meteorological Service.
The local walnut species cultivated in the research area are Şebin and Bilecik, while Chandler and Pikan are the foreign species that provide high efficiency and high-quality full fruits inside thin shells, thus yielding high income. The walnut orchards in the research area vary between 5 and 10 ha in size. The young trees in the orchards are generally planted within 9 × 9 and 10 × 10 m spaces.
All the information that was needed for the planning of the irrigation system, the sizing of the system elements, and the configuration and operation of the system were obtained through terrain analyses. Following these efforts, the drip irrigation project was prepared and set up in the orchard. The drip irrigation system consisted of the water source, pumping unit, control unit, pipelines and drippers. Irrigation water was filtered taking care not to clog the drippers and then mixed with the necessary nutrients. After the pressure and flow rate checks, it was distributed to the research plots. The control unit was made up of a fertilizer tank, a strainer filter and manometers for pressure control. Soil samples were taken and analyzed according to Blake (1965) and Benami and Diskin (1965). The soil texture was measured with a hydrometer as explained in Bouyoucos (1962). Irrigation water quality analyses were performed in the laboratory, in accordance with USDA (1954). The actual value of infiltration rate was identified (Criddle et al., 1956) by double ring infiltrometer measurements.
2.2 Data collection, description and analysis
The raw data set (Table I) to be used in the model includes the parameters of maximum, minimum and average temperatures (Tmax, Tmin and Tavg, respectively), wind speed (u2) and sunshine hours (n). The reference dataset in this study was the calibrated climate data from regional weather stations for the period 2016-2019, provided by the Turkish State Meteorological Service (TSMS, 2022). The averages of annual temperature, wind speed, and the sunshine duration recorded between the first and last frost dates were 20.50 ºC, 1.92 m s−1, and 6.9 h, respectively, while the highest values of maximum and minimum temperatures were 40.7 and 31.9 ºC, and the lowest values 12 and 2.5 ºC. The extreme values for all meteorological parameters were observed during these years. Therefore, the raw data set was subjected to quality control by removing 5% of noisy data from the data set.
Table I Ranges of the raw dataset based on statistic terms across the study region for 2016-2019.
| Parameters | Data statistics | Units | |||
| Maximum | Minimum | Mean | SD | ||
| Tavg | 32.7 | 6.6 | 20.5 | 5.058 | ºC |
| n | 12.8 | 0.0 | 7.0 | 3.769 | h |
| Tmax | 40.7 | 12.0 | 26.8 | 5.706 | ºC |
| Tmin | 31.9 | 2.5 | 15.8 | 5.002 | ºC |
| u2 | 4.6 | 1.1 | 1.9 | 0.432 | m s-1 |
| ETc | 7.9 | 0.5 | 3.7 | 2.059 | mm day-1 |
SD: Standard deviation.
The reference evapotranspiration was calculated based on the PM-FAO method in Eq. (1), using meteorological data (Allen et al., 1998).
where ETo is the reference ET (mm d-1), Rn is the net radiation (MJ m-2 d-1), G is the soil heat flux density (MJ m-2 d-1), T is the mean daily air temperature (ºC), Δ is the slope of the saturation vapor pressure function (kPa ºC-1), γ is the psychometric constant (kPa ºC-1), e s is saturation vapor pressure (kPa), e a is the actual vapor pressure (kPa), and u 2 is the mean daily wind speed (m s-1).
The crop evapotranspiration is calculated by multiplying the reference crop evapotranspiration by a walnut crop coefficient and described as:
where ET c is the crop evapotranspiration (mm d-1), k c is the crop coefficient (dimensionless), and ET 0 is the reference crop evapotranspiration (mm d-1).
The growing season was observed regularly in the field throughout the study period from the first frost on April 15 to the last frost on November 10. During this period, four major growing stages were distinguished as the initial, crop development, mid-season and late season stages. Accordingly, the corresponding K c values were adopted from investigations by the General Directorate of Agricultural Research and Policies for a specific region in Kocaeli as K cini = 0.41, K cmid = 1.17 and K cend = 0.77.
The data were normalized from 0 to 1 based on Eq. (3) to ensure they remained within a certain range and the statistical distribution was uniform when scaling.
where X i is raw data, X min is the minimum value of X, X max is the maximum value of X, and Y is the standardized data value.
2.3 Probabilistic scenarios
The ReliefF feature selection algorithm, which is a filter feature selection method modified by Kira and Rendell (1992), was used to filter the data and sort them according to their weight values between -1 (worst) and +1 (best). The processing procedure was repeated for each attribute and the weight value of each attribute was calculated at the end (Köksal, 2020; Sattari et al., 2021). A series of probabilistic scenarios based on ReliefF results were created to be used in the artificial intelligence models. Matlab R2016a was used to implement ANN and ANFIS models and Weka 3.9.4 modules were used to implement ReliefF.
2.4 Artificial intelligence methods
2.4.1 Artificial neural networks
An ANN model was created for each probabilistic scenario obtained from the ReliefF algorithm. Once the probabilistic scenarios were created as model input, the entire dataset was randomly split. The reason for the random division of the data was the increase and decrease of climatological parameters during the development period (Yu et al., 2020; Pandey and Pandey, 2020). Different percentages of data sets (training, validation, and testing) were applied at a rate from 75 to 85% for training, 0 to 10% for validation, and 15 to 20% for testing in each ANN model. There is no specific and accepted methodology for the network architecture created to determine the best performance of ANN (Wu et al., 2014; Antonopoulos et al., 2015). Therefore, neuron numbers were determined by trial and error for the best performance in all probabilistic scenarios. The performance of each model was evaluated according to R2 and MSE (Sagi and Jain, 2020; Adeloye et al., 2012), and the best scenario was selected.
2.4.2 Adaptive neuro-fuzzy inference system
The model was run with the five input parameters (Tmax, Tmin, Tavg, u2, and n) using the Matlab R2016a module to implement ANFIS. In the model, different membership functions were used to minimize each parameter’s error. The dataset was implemented between 60-80% for training and 20-40% for testing.
3. Results
3.1 Results of data analysis and probabilistic scenarios
The real data set consists of 879 rows with the five meteorological parameters covering the growth periods of 2016-2019. When the dataset was examined after the data analysis, the mean T avg remained approximately constant, while the standard deviation decreased from 5.058 to 4.46. In addition, three outliers were removed from the dataset because unexpected records could create a bias in the model. As a result, the maximum and minimum values of T avg for four years were prepared for the model as 28.9 and 9 ºC, respectively.
According to the analysis results for maximum and minimum temperatures, the four peak values and the three lowest maximum temperature values were removed from the dataset, and it was found that Tmax decreased from 40.7 to 37.4 ºC. In addition, it was found that while the mean maximum temperature value increased, the standard deviation value decreased from 5.706 to 4.853. On the other hand, it was determined that the average minimum temperature value increased from 15.8 to 16.3 ºC. Following this, there was a decrease in the minimum temperature deviation from the mean.
As can be seen in Figure 2, the wind speed set does not show a uniform distribution, but there are a few values above 3 m s-1. When these data are removed (see Fig. 3), the maximum and minimum wind speeds are 2.9 m s-1 and 1.1 m s-1, respectively, and a uniform distribution is formed with 1.89 m s-1.
No specific data was observed in the sunshine duration data, so it was removed from the dataset. However, due to the other parameters that were removed, the dataset was positively affected. For this reason, the average mean sunshine duration increased from 6.69 to 7.32 h, but the standard deviation value decreased from 3.769 to 3.563.
In summary, from the set of 891 data, 57 were removed, corresponding to 6% percent of the total dataset. Of the 879 datasets, 45 were reserved for verification and not included in the models. Therefore, 834 datasets were used in the training, validation and testing stages. According to the data analysis results, it was concluded that the standard deviation value decreased in all parameters and the mean values remained approximately constant.
The aim of proposing these scenarios was mainly to determine whether there was a high correlation with models that have descending probabilistic input parameters. The ReliefF algorithm was used to rank the five selected input parameters to estimate the output parameter of each AI model. The algorithm results for all input parameters are shown in Table II.
Table II Ranges of the dataset based on statistic terms across the experimental region for 2016-2019 and ReliefF ranking.
| Parameters | Maximum | Minimum | Mean | SD | ReliefF-ranked attributes | Units |
| Tavg | 28.9 | 9.0 | 21.1 | 4.460 | 0.002422 | ºC |
| n | 12.8 | 0.0 | 7.3 | 3.563 | 0.001214 | h |
| Tmax | 37.4 | 15.3 | 27.7 | 4.853 | 0.001021 | ºC |
| Tmin | 24.3 | 3.1 | 16.3 | 4.602 | 0.000719 | ºC |
| u2 | 2.9 | 1.1 | 1.9 | 0.356 | 0.000371 | m s-1 |
| ETc | 7.5 | 0.9 | 3.9 | 1.943 | - | mm day-1 |
SD: Standard deviation.
According to the results of the relief algorithm, the input parameters were arranged in order of importance and various scenarios were created by reducing the number of parameters one by one (i.e., starting with six parameters and then reducing them to five, four, etc.). In the new scenarios generated in this manner, the accuracy of the model may increase or decrease. This reduction model can be expected to be at an acceptable level of performance (see Table II). Table III shows different inputs based on alternative scenarios. In the first scenario, the model is run using all input parameters. Then, in each scenario, the accuracy of the model was reassessed with one missing parameter.
3.2 Crop water use estimation by artificial neural networks
Various training functions and different numbers of neurons were used to investigate the best performance. A trial and error approach was adopted to find the optimum number of neurons. The randomization of the hidden layer’s neurons was found to be between six and three neurons in parallel with the input parameter. In the hidden layer, the values with the best number of nodes and lowest error were used.
In the models created with ANN, the MSE and R2 values were obtained by running each model 15 times on average. As shown in Table IV, over-learning was detected in scenarios 1, 2 and 3 despite optimizing the number of neurons. To solve this problem, 5% of the dataset was used for the validation part. It was concluded that the best training performance of the models was in the first scenario with an R2 of 0.91. However, it was concluded that R2 and MSE values remained constant when the wind speed, and the maximum and minimum temperatures were removed in other scenarios. Accordingly, when Scenario 4 was examined, it was seen that the R2 values for training and testing were 0.90 and 0.89, and MSE values for training and testing were 0.9324834 and 0.9306326 mm day-1, respectively. On the other hand, due to the fact that the value of R2 with a single parameter was 0.78 in Scenario 5 and the errors in the estimation increased, it was not considered appropriate for the model estimation. As a result, Scenario 4, which had the highest correlation, minimum mean square error, and minimum input parameter was considered to be the best model.
Table IV Performance of each scenario based on the ANN model for training, validation and testing.
| Output parameter | Scenario | Performance | |||||||||
| Training (%) | Validation (%) | Testing (%) | MSE | R2 | |||||||
| Training | Validation | Testing | Training | Validation | Testing | ||||||
| ETc | 1 | 80 | 5 | 15 | 0.9279886 | 0.9096128 | 0.9410764 | 0.92 | 0.95 | 0.89 | |
| 2 | 80 | 5 | 15 | 0.9275259 | 0.9271293 | 0.9349952 | 0.91 | 0.92 | 0.88 | ||
| 3 | 80 | 5 | 15 | 0.9326156 | 0.9227667 | 0.9398205 | 0.90 | 0.91 | 0.88 | ||
| 4 | 80 | - | 20 | 0.9324834 | - | 0.9306326 | 0.90 | - | 0.89 | ||
| 5 | 80 | - | 20 | 0.9930310 | - | 0.9824550 | 0.80 | - | 0.77 | ||
MSE: mean square error; R2: coefficient of determination.
Even when high correlation is found throughout the network training, testing and validation phases, the models still need to be verified to prove that they perform accurate estimations. The 45 datasets that were not used in the training, validation and testing of the ANNs model were separated as one value for each month and used in verification. Each probabilistic scenario was used while verifying the model. The graphs between the predicted and observed values for all parameters are shown in Figure 4.
3.3 Crop water use estimation by ANFIS
In the generated probabilistic scenarios, the data sets were manually distributed as 80 and 20% for training and testing, respectively. Membership functions (MF) that are used in training ANFIS models are functions used to determine the classes of values. The MF type is of great importance in training the network. For this reason, “gaussmf” and “gauss2mf” functions with the lowest error margin were selected by trial and error for all applied MF types.
It was found that the smallest MSE in the ANFIS model was 0.209896 mm day-1 in Scenario 1 with five input parameters (Tavg, n, Tmax, Tmin and u2), and 0.701142 mm day-1 in Scenario 5 with only one input (Tavg). It was concluded that R2 values of scenarios 1, 2, 3, and 4 remained constant despite the decrease in parameter numbers. It was found that values for Scenario 4 were 0.364975 and 0.294885 mm day-1 for training and testing, respectively, while in Scenario 5 these values increased to 0.701142 and 0.898864 mm day-1. On the other hand, while values for R2 were 0.90 for both training and testing in Scenario 4, it was found to be 0.81 for training and 0.79 for testing in Scenario 5. Therefore, it was concluded that Scenario 4 was more successful in estimating crop water use (see Table V).
Table V Performance of each scenario based on the ANFIS model for training, validation and testing.
| Output parameter | Scenario | Performance | |||||||||||
| Training (%) | Testing (%) | Number of MFs | MF type | Epochs | Number of nodes | Non-linear parameters | Fuzzy Rules | MSE | R2 | ||||
| Training | Testing | Training | Testing | ||||||||||
| ETc | 1 | 80 | 20 | 3 | gaussmf | 41 | 524 | 30 | 243 | 0.209896 | 0.355707 | 0.94 | 0.88 |
| 2 | gauss2mf | 49 | 193 | 48 | 81 | 0.277951 | 0.258986 | 0.92 | 0.91 | ||||
| 3 | gaussmf | 90 | 78 | 18 | 27 | 0.337374 | 0.296796 | 0.90 | 0.90 | ||||
| 4 | gaussmf | 123 | 35 | 12 | 9 | 0.364975 | 0.294885 | 0.90 | 0.90 | ||||
| 5 | gauss2mf | 73 | 16 | 12 | 3 | 0.701142 | 0.898864 | 0.81 | 0.79 | ||||
MF: membership functions; MSE: mean square error; R2: coefficient of determination.
3.3.1 Model verification
The same 45 data sets used in ANN models were also used for the verification of ANFIS models. The most advantageous aspect of the model verification dataset is the presence of parameters that are not trained by the model. For example, while the highest and lowest model-trained ETc values were 7.49 and 0.88 mm day-1, the highest and lowest ETc values in the validation dataset were 7.92 and 0.51 mm day-1. In other words, ANFIS models can predict even the highest and lowest values in all scenarios which they have not encountered before with the lowest rate of error. Figure 5 shows the observed and estimated crop water use values.
3.4 Performance of the Penman Monteith approach for crop water use
ETc values obtained from the Penman approach, considering multiple climate parameters and plant characteristics, were plotted in Figure 6 together with the verification results used for the scenario proposed in the models. As seen in the figure, the results of the model obtained with a few parameters are in parallel with Penman’s results, and the ANFIS and ANN models have the highest statistical correlation (-0.349 and -0.361, respectively) according to the comparison (two-simple t test) .
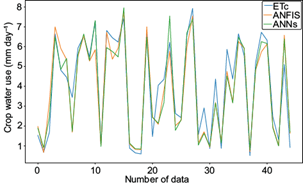
Fig. 6 Crop water use changes obtained by empirical and predicted model consisting of ANN and ANFIS.
Considering the predicted ETc, rainfall and also the 2-year phenological follow-ups, it was determined that irrigation must be initiated at the beginning of April when walnut trees are forming leaves and blossoming, and continued through October. If the trees are unable to get enough water during this period, growth and vegetation will slow down and there will be decreases in quality and efficiency, since fruits will not be able to grow enough meat. It is prescribed that in walnut areas with similar climate and soil characteristics as the study area, irrigation can be performed every 3-4 days in the summertime.
4. Discussion
Many studies explain that ANN, ANFIS, and other machine learning methods can outperform traditional computational methods on the prediction of evaporation and evapotranspiration to explain the effect on agricultural water use (Adeloye et al., 2012; Kisi et al., 2015; Abrishami et al., 2018; Sanikhani et al., 2019; Yamaç and Todorovic, 2020; Elbeltagi et al., 2020; Petković et al., 2020; Yamaç, 2021; Sattari et al., 2021). Al-Mukhtar (2021) and Goyal et al. (2014) proposed and predicted E with high accuracy using these models and performance. In this study, the estimation results of plant water use were evaluated using the artificial intelligence methods of ANN and ANFIS with few parameters, including average temperature (Tavg) and sunshine duration (n). Terzi and Keskin (2005) predicted daily panevaporation using the ANN model with six meteorological variables in the Eğirdir lake region. Deswal and Pal (2008) used ANN to investigate the impact of various collections of meteorological parameters on water surface evaporation. They found that the most effective parameter in probabilistic scenarios created for the model is average temperature. Through scientific studies, it has been demonstrated that maximum, minimum and average temperatures are more successful than other climate parameters in estimating evapotranspiration using artificial intelligence models (Abyaneh et al., 2011; Tabari et al., 2013; Aghajanloo et al., 2013; Yamaç and Todorovic, 2020; Sattari et al., 2021).
According to the ANN and ANFIS results in this study, these models had an acceptable performance with high accuracy R and low mean square error to estimate ET. It was also concluded that ANFIS has a better performance than ANN. Likewise, Karimi et al. (2012) stated that the ANFIS model gave better results than ANN.
Numerous studies sustain that the results of various machine learning methods (including ANN and ANFIS) are more certain and accurate regarding crop water consumption and evaporation compared to empirical methods. Many researchers have used artificial intelligence models to predict evapotranspiration, finding that they give better results (Abyaneh et al., 2011; Feng et al., 2017; Nourani et. al., 2019; Hashemi and Sepaskhah, 2020; Yamaç and Todorovic, 2020; Gao et al., 2021; Hadadi et al., 2022). Also, our results are in accordance with Kisekka and Peddinti (2022), who observed a statistically strong relationship with similar models between walnut ETc and different input variables.
5. Conclusion
The application of ANN and ANFIS in the fields of hydrology, water management, and environmental and agricultural studies, including agriculture and ET estimates, has increased in the last years. In this study, ANN and ANFIS were introduced to predict ET and investigate their modeling performance with different scenarios of meteorological input data availability. In this context, estimated ET was simulated by different machine learning methods and was compared to detailed empirical data. This methodology allowed to quickly produce statistically reliable predictions with less data, which in turn allowed to determine the evapotranspiration of walnut trees and their fruits in the Marmara basin of Turkey. These results will also assist in the determination of crop ET under limited water supply and stress conditions in terms of irrigated agriculture and efficient water use.











 nueva página del texto (beta)
nueva página del texto (beta)







