1. Introduction
The desert of the north coast of Peru (NCP) (Ramos, 2015) can swiftly change into a rainy green oasis when abundant rainfall occurs during El Niño conditions, which can be defined as a positive anomaly of sea surface temperature (SST) above 0.4 ºC in the 3.4 region of the Pacific Ocean during a five-month running mean over six months (Trenberth, 1997). The rise in SST typically generates changes in the global atmospheric circulation, which can enhance rainfall and storms in different parts of the world, such as South America and the Peruvian and Ecuadorian coasts.
The change from desert-like conditions to a tropical rainy climate in the NCP negatively impacts several economic activities such as fishing, agriculture, and trade, as discussed by Sanabria et al. (2018), Sulca et al. (2018), and Yglesias-Gonzáles et al. (2023). It is estimated that extreme El Niño events cause losses of over 3 billion dollars to the Peruvian economy and more than 300 casualties due to flash floods, infrastructure damage, and illnesses enhanced by the wet conditions, such as dengue and cholera (e.g., CAF, 2000; OPS, 2017; Quispe, 2018). For instance, one of the strongest El Niño events developed in 1997-1998, which exhibited temperatures greater than +2.4 ºC above climatology in the central Pacific (CPC, n.d.). This event generated extreme rainfall rates in the NCP and a mild winter all along the Peruvian coast (Pantoja, 2004). Similarly, a warming of the SST off the coast of Peru (known as a coastal El Niño) was identified in the austral summer of 2017, an event that had not been observed since 1925 (Takashi and Martínez, 2019). Both of these events generated precipitation totals that exceeded the 90th percentile over the NCP as well as the north and central Andes (Sanabria et al., 2018; Rodríguez-Morata et al., 2019). The aforementioned increased precipitation due to El Niño events is explained by the occurrence of particular circulation patterns. Three main levels are considered when analyzing this potential for enhanced precipitation: the upper levels (300 to 200 hPa), the mid-levels (700 to 500 hPa), and the low levels (from the surface to 850 hPa).
The upper levels of the atmosphere are primarily governed by the Bolivian High (BH) and the Nordeste Low (NL) during the austral summer (Sulca and da Rocha, 2021). The BH, located in El Chaco (subtropical South American rain forest), provides easterly flow and divergence at upper levels. The NL traps dry air conditions and suppresses convection at its core. The formation of the BH is crucial for the onset of the rainy season in the central and northern Andes because it brings moisture from the Amazon basin in mid-levels and divergence in the high levels of the atmosphere (Garreaud, 1999). Quispe (2018) noted a similar process occurs in the north Peruvian Andes, where the coupled BH and NL systems can produce positive divergence aloft (enhancement of precipitation), along with an area of upper-level divergence off shore of the NCP. This feature has been identified as the upper-level mechanism that supports the formation of the second band of the Intertropical Convergence Zone (ITCZ) (Masunaga and L’Ecuyer, 2010).
The mid-levels of the atmosphere present a key component for precipitation over the NCP. Aliaga-Nestares et al. (2022) showed that moisture advection at 600 hPa in the NCP (westerly flow) is essential for the organization of convective systems and the second band of the ITCZ. Quispe (2018) noted mixing ratio values over 9 g kg-1 at 700 hPa and 4 g kg-1 at 500 hPa are most correlated with convective activity enhancement in the NCP.
The presence of the South Pacific Anticyclone and the trade winds strongly influence the lower levels of the atmosphere. In the summer of 2017, anomalous northerly and westerly winds developed off the coast of Ecuador and the NCP, advecting moisture over land and also forming a second convergence band at 925 hPa, which has been identified as the second band of the ITCZ (Quispe, 2018). A similar process was found by Aliaga-Nestares et al (2022). They found that a warming of SST above 27 ºC during the 2017 coastal El Niño caused a change in wind direction to northerlies and westerlies off the coast of Ecuador and Peru, creating convergence near the surface and bringing in moisture from the warm Pacific.
Even though there is substantial research on the topic of El Niño, it is focused on the climate scale (e.g., Trenberth and Hoar, 1997; Takahashi et al., 2011; Cai et al., 2020), and large-scale circulation patterns (Quispe, 2018; Aliaga-Nestares et al., 2022). There is no prior research focused specifically on techniques to improve precipitation diagnosis and operational weather forecasting skill in the NCP under El Niño conditions. This study aims to develop a new index for precipitation diagnosis in the NCP using logistic regression (LR), which is a regression technique that explains the relationship between a categorical variable and one or more predictor variables (Peng et al., 2002). For example, Samasti and Küçükdeniz (2023) used LR to forecast precipitation in Amasya, Turkey during the rainy season of 2020 (September to December). The forecast was based on 10 years (2010-2019) of rainfall data from 241 weather stations used as predictand and the maximum and minimum temperature as predictors. Their LR model had an accuracy rate of 84%, where they found out that the minimum/maximum temperature had a positive/negative relationship with precipitation. Knowing the rainy days improved harvest efficiency by 16% compared to other years. Applequist et al (2002) compared different linear and nonlinear methodologies for quantitative precipitation forecasting in the central and eastern United States during the cold season (December to March from 1992 to 1996). They showed that LR works best compared to linear regression, neural networks, discriminant analysis and classifier systems at the 99% confidence level. Pang et al. (2019) performed a study in Guangdong, China from March to April 2014, where they used LR to analyze the relationship between severe convective weather and multiple instability indices such as the K index and the Total Totals index. Their LR-based prediction for severe convective precipitation was found to have an improved critical success index over other traditional indices (e.g., K, Total Totals). These studies show the importance of LR as a tool to improve the rainfall forecast for the wet season, especially in areas void of accurate forecast or severe weather instruments.
Many indices have been developed over the years to improve precipitation or storm prediction. For instance, an early example was the Showalter index, where an air parcel is adiabatically lifted from 850 to 500 hPa and the temperature difference between the parcel and the environment is used to detect elevated convection (Showalter, 1953). Other indices include moisture in the calculations, such as the K index (George, 1960) and, more recently, the Gálvez-Davison Index (GDI), which includes numerous calculations and subindices that evaluate column buoyancy, mid-tropospheric warming, and thermal inversions at levels such as 950, 850, 700, and 500 hPa. The GDI can successfully predict deep convection and precipitation in the Caribbean (Gálvez and Davison, 2016).
This study aims to develop a new diagnostic tool for precipitation in the NCP using LR. Satellite-based surface rain data from the Tropical Rainfall Measurement Mission (TRMM) and the Global Precipitation Measurement Mission (GPM) are used as predictors, while ERA5 data are used as predictors for the logistic model. In section 2, the area of study is described, and the methodology to filter the satellite data based on thresholds for rainy days and non-rainy days for the LR model is detailed, as well as further analysis of the predictions made by the LR model using a contingency table and statistical metrics. Section 3 portrays the results of multiple LRs based on different combinations of predictors and thresholds, ultimately determining the best combination to form the new precipitation diagnostic index named RAMI, which is evaluated pixel-by-pixel and compared with other indices. Finally, research conclusions are presented in section 4.
2. Data and methodology
2.1 Area of study
This study focuses on developing a new index for precipitation diagnosis in the NCP, which encompasses the three states of northern Peru, namely Tumbes, Piura, and Lambayeque. The NCP region (shown in Fig. 1 as a black box) includes five subregions, each with specific physical and geopolitical characteristics listed in Table I.
Table I Description of regions.
| Region | Latitude | Longitude | Color* |
| Total | -3.25; -7 | -81.5; -79.5 | Black |
| Tumbes | -3.25; -4 | -81; -80 | Green |
| Amotape Mountains (AM) | -4; -5 | -81.5; -80 | Red |
| Northern Andes (AN) | -4.5; -6.25 | -80; -79.25 | Blue |
| Sechura desert | -5; -6.25 | -81.25; -80 | Cyan |
| Lambayeque (Lam) | -6.25; -7 | -81; -79.25 | Magenta |
*Color assigned to the region in Figure 1.
The NCP has mainly an arid tropical climate with moisture deficiency. It has been classified by SENAMHI (2020) as E(d)A' of the Thornthwaite climate classification scheme (Feddema, 2005). Geographically, it is considered mainly from sea level to approximately 900 masl. It also presents a mountain range named the Amotapes that separates Tumbes and Piura from Ecuador, with altitudes up to 1600 masl. Its climate presents temperatures ranging from 13 to 33 ºC and annual precipitation from 20 to 50 mm year-1. However, these values are exceeded under the influence of El Niño (SENAMHI, 2020). Demographically, the NCP is home to 3.6 million people, which represents 11% of Peru’s population. Its most populated city is Piura (capital of the Piura state), which has 2 million inhabitants.
2.2 Data
The satellite-based TRMM (Simpson et al., 1996) and GPM (Hou et al., 2014) estimations of rainfall amount and distribution serve as the study’s training dataset. The University of Washington’s TRMM and GPM-Ku data websites (UW, 2022a, b) were used to download the data. We used version 6 of the data for South America from 1998 to 2013 for the TRMM and from 2014 to 2021 for the GPM. Both datasets present a 0.05º spatial resolution and a one-time temporal resolution per file, which belongs to the exact time of the swath pass at a given time of day. The satellite passes roughly twice daily (ascending and descending swaths).
The second dataset in the study is the ERA5 (ECMWF reanalysis 5) (Hersbach et al., 2020). The selected meteorological variables were temperature, geopotential height, relative humidity, specific humidity, zonal wind, and meridional wind. The data was downloaded for the mandatory atmospheric pressure levels (1000, 975, 950, 925, 900, 850, 700, 600, 500, 400, 300, 250, and 200 hPa) to match the mandatory pressures currently used in operational applications, at 0.25º horizontal resolution and three-hourly time resolution (e.g., every 3 h, from 00:00 to 21:00 UTC).
2.3 Methodology
TRMM and GPM satellite data from the months of January, February, March, and April from 1999 to 2021 were used to determine the days when rain was or was not present during the study period in the different NCP regions. This pre-processing shifted the satellite data into categorical binary data in which a value of 1 indicates a “rainy day” and a value of 0 indicates a “non-rainy day”. If rain is present inside one of the regions at the time of the satellite swath, and the total rainfall amount inside the region is above a certain precipitation threshold (PT), that day is counted as a “rainy day” for that particular region at that particular time. Conversely, if there is no rain within or the total amount of precipitation inside the region at a given time is below the PT, that day is counted as a “non-rainy day”. Examples of a “rainy day” and a “non-rainy day” are depicted in Figure 2.
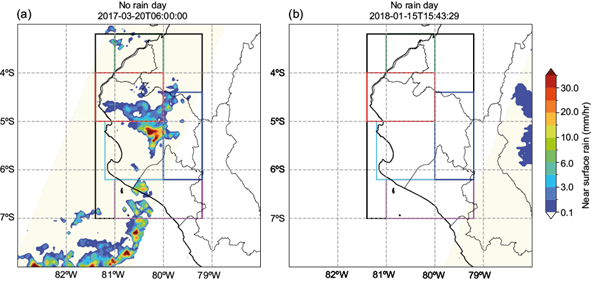
Fig. 2 Examples of (a) “rainy day” and (b) “non-rainy day”. Both are defined using the total area (black). Surface rain from the Global Precipitation Measurement Mission (GPM) is shown with color-filled contours.
Five PTs were tested to evaluate the sensitivity of this approach to the chosen threshold (25, 50, 100, 150, and 200 mm per region). PTs were chosen based on the region’s climatology of precipitation, given that precipitation only occurs in the rainy season (January to April). The rainfall rates range between 25-50 mm per region, and there may be even more extreme cases where rain may reach 200 mm or more. The sensitivity of rainy days to different PTs is shown in Table II. The region’s size strongly impacts the number of rainy days identified, although there is a slight decrease in the number of rainy days towards the south, as expected from the region’s climatology. The time of the precipitation taken for a “rain” or “non-rainy day” is given by the time of the satellite swath. The polar-orbiting satellite passes over the region at different times of the day. As shown in Figure 3, rainfall detections can occur at any hour of the day. Nevertheless, we suspect that our long-term analysis (1998-2001) allows us to have confidence in the representativeness of the data. For example, the diurnal cycle derived from Figure 3 is supported by the nature of the convective episodes, i.e., rainfall is more frequent in the late evening and night (20:00-06:00 LT) and less frequent in the afternoon (12:00-14:00 LT).
Table II Number of rain and non-rainy days found for each region per precipitation threshold from January to April 1998-2021.
| Region | Color* | 25 mm | 50 mm | 100 mm | 150 mm | 200 mm |
| Total | Black | 1015 | 883 | 743 | 669 | 615 |
| Tumbes | Green | 519 | 448 | 390 | 372 | 353 |
| Amotape Mountains (AM) | Red | 522 | 459 | 416 | 386 | 370 |
| Northern Andes (AN) | Blue | 629 | 555 | 481 | 444 | 421 |
| Sechura desert | Cyan | 446 | 414 | 390 | 382 | 372 |
| Lambayeque (Lam) | Magenta | 456 | 423 | 398 | 387 | 380 |
*Color assigned to the region in Figure 1.
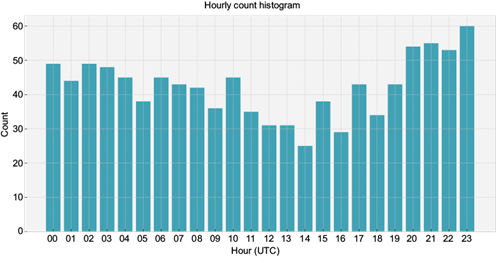
Fig. 3 Histogram of the number of rain and non-rainy days using a PT of 25 by the hour (UTC) of the day for the total study region (black box in figure 1).
The date and time of the swath pass from the satellite were used to determine the nearest time for the corresponding ERA5 data at 3-hourly temporal resolution (00:00, 03:00, 06:00, 09:00, 12:00, 15:00, 18:00, and 21:00 UTC). Table III displays the ERA5 meteorological variables calculated and used as predictors to train the LR.
Table III Secondary meteorological variables calculated from the ERA5 data.
| Variable | Level |
| Mixing ratio | 700, 600, 500 hPa |
| Equivalent potential temperature | 950, 850, 700, 500 hPa |
| Divergence | 950, 850, 250, 200 hPa |
| Wind shear | 1000-400 hPa |
| Vorticity | 500 hPa |
| Precipitable water | 1000-200 hPa |
| CAPE | Equilibrium level-level of free convection |
| Lifted index | 500 hPa |
| Total Totals index | 850, 500 hPa |
| K index | 850, 700, 500 hPa |
| Gálvez-Davison Index | 950, 850, 700, 500 hPa |
CAPE: convective available potential energy.
The LR model starts with a traditional linear regression, establishing a relationship between the categorical variable (rain or no rain) and the established set of ERA5 predictor variables candidates. Using a logit function, the results are mapped onto binary outcomes, with 0 representing a prediction of no rain and 1 representing a prediction of rain. To train the LR model, a group is randomly selected containing 80% of the total rain and non-rainy days for the LR, and the remaining 20% of the data is saved for validation purposes. This separation of 80 and 20% is done for every region and every PT.
Each variable was first used to train its own LR to determine its individual relationship with precipitation, as measured by its odds ratio value. Later, variables with the best odds ratios were evaluated with LRs trained on every combination of 2, 3, 4 … n (in which n is the total number of variables considered). To determine which combination yields the best result, a contingency table comparing observed precipitation (GPM and TRMM) against precipitation predicted by LR (Table IV) was chosen to calculate the metrics given below.
Table IV Contingency table of observed vs. predicted rain.
| Contingency table | Observed | ||
| Yes | No | ||
| Predicted | Yes | True positive (a) | False positive (b) |
| No | False negative (c) | True negative (d) | |
Probability of detection (POD), the fraction of successfully predicted events:
False alarm ratio (FAR), the fraction of unsuccessful predictions:
Critical success index (CSI), the fraction of successful predictions compared to the total number of predictions and events:
3. Results and discussion
3.1. Individual logistic regression by variable
The first step is to perform a randomized LR, where a LR is built 1000 times; each time a random 80% of the data is selected to train the model, with the remaining 20% left for validation purposes. The variables to be considered in the multivariate LRs were selected based on an odds ratio threshold (ORT). If the odds ratio of a given LR has a value outside of the 0.9 to 1.1 range, it is counted as a good correlation: a variable needs to have an odds ratio outside of the ORT in at least 500 out of the 1000 attempts to be selected as part of the LRs created (see section 3.2). The study found that the convective available potential energy (CAPE), the equivalent potential temperature at all levels, vorticity, and wind shear are not outside the ORT range, indicating little skill in predicting rainfall alone. Since CAPE is calculated based solely on the mandatory atmospheric levels (see section 2.2), it lacks vertical resolution and more near-surface information compared to CAPE calculated based on a sounding with many vertical levels and detailed near-surface information. In contrast, the variables that have the most instances outside the ORT range are listed as follows: the composite storm indices such as the GDI and Lifted Index, K index, and Total Totals index; divergence at 200, 250, 850, and 950 hPa; precipitable water (PWAT); and the mixing ratio. This last variable is in 100% of the cases outside the ORT at all troposphere levels. The mixing ratio also shows an odds ratio greater than 1.5 more than 80% of the time (Table V).
Table V Percentage of the 1000 randomized LR iterations outside the ORT for each meteorological variable.
| Selected | Variable | Odds ratio count | |||||
| ≥ 1.1 | ≥ 1.25 | ≥ 1.5 | ≤ 0.9 | ≤ 0.75 | ≤ 0.5 | ||
| Yes | Divergence 200 | 70.0 | 30.7 | 3.2 | 2.4 | 0.2 | 0.0 |
| Divergence 250 | 69.8 | 30.9 | 3.2 | 2.5 | 0.2 | 0.0 | |
| Divergence 850 | 0.4 | 0.1 | 0.0 | 93.3 | 52.3 | 3.0 | |
| Divergence 950 | 0.5 | 0.1 | 0.0 | 79.7 | 53.7 | 2.4 | |
| GDI | 50.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| K Index | 100.0 | 96.4 | 71.3 | 0.0 | 0.0 | 0.0 | |
| Lifted Index | 0.0 | 0.0 | 0.0 | 100.0 | 91.5 | 14.1 | |
| Mixing ratio 500 | 100.0 | 99.9 | 95.8 | 0.0 | 0.0 | 0.0 | |
| Mixing ratio 600 | 100.0 | 100.0 | 98.1 | 0.0 | 0.0 | 0.0 | |
| Mixing ratio 700 | 100.0 | 99.8 | 83.4 | 0.0 | 0.0 | 0.0 | |
| PWAT | 100.0 | 41.8 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Total Totals Index | 97.7 | 77.1 | 31.0 | 0.0 | 0.0 | 0.0 | |
| No | CAPE | 0 | 0 | 0 | 0 | 0 | 0 |
| EPT 500 | 25.2 | 14.3 | 2.3 | 0.0 | 0.0 | 0.0 | |
| EPT 700 | 25.1 | 14.0 | 2.3 | 0.0 | 0.0 | 0.0 | |
| EPT 850 | 22.6 | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| EPT 950 | 43.5 | 10.7 | 0.0 | 0.0 | 0.0 | 0.0 | |
| U_wind shear 1000-400 | 0.0 | 0.0 | 0.0 | 2.4 | 0.0 | 0.0 | |
| V_Wind Shear 1000-400 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Vorticity 500 | 17.7 | 1.9 | 0.1 | 17.0 | 0.4 | 0.0 | |
LR: logistic regression; ORT: odds ratio threshold; GDI: Gálvez-Davison Index; PWAT: precipitable water; CAPE: convective available potential energy; EPT: equivalent potential temperature.
3.2. Best combination of variables
Once the 12 variables are selected, a new set of LRs is performed with every possible combination of these variables for each region, different PTs (total amount of precipitation needed in each region to be considered a rainy day: 25, 50, 100, 150, and 200 mm region-1) and different validation thresholds (VT) (value of the output of the LR equation to be considered as a predicted rainy day: 60, 70, and 80). For this study, the data is split again randomly into 80% for training and 20% for validation so that the new set of LRs are mutually comparable using the contingency table and the validation metrics introduced in section 2.2. Due to the high number of combinations evaluated, each combination is displayed using box plots for each metric shown (Figs. 4-6).
POD (Fig. 4) tends to have lower values as the VT and PT increase. The best POD is achieved for the total area with a VT of 60 and a PT of 25 (top left panel in Fig. 4). The other sub-regions (Fig. 1) do not include values of POD as high as the total region, with values usually below 0.6; thus, smaller areas of interest do not equate to a better ability to predict precipitation. The total area shows little variability in FAR across all VT and PT (Fig. 5), while the other regions have higher variability, especially when VT and PT increase. The best balance between low FAR and high POD was found to be a VT of 60 and a PT of 50.

Fig. 4 Probability of detection (POD) plotted by region for all combinations of PT, VT, and all combinations of selected variables (MR 700, 600, and 500; Lifted Index; K Index; divergence at 950, 850, 250, and 200 hPa; Total Totals; GDI, and PWAT). Columns present VT of 60, 70, and 80, while rows present PT of 25, 50, 100, 150, and 200 mm per region. Missing boxplots indicate that there were no predicted values for rain in its respective LR model. (PT: precipitation threshold; VT: validation threshold; MR: mixing ratio; GDI: Gálvez-Davison Index; PWAT: precipitable water.)
The CSI (Fig. 6) combines POD and FAR into a single metric. The total area has the least variation, and while many of the smaller regions have little variation among the VT and PT values, the spread increases with higher values of PT (bottom two rows of Fig. 6). The highest value of the CSI (0.66) was found for six different combinations of variables (Table VI), which all have a VT of 60 and a PT of 50. The combination of mixing ratio at 700 hPa, divergence at 950 and 250 hPa, and GDI was selected because it shows the same variables that were described in the circulation patterns for precipitation in the NCP by Quispe (2018) and Aliaga-Nestares et al. (2022).
Table VI Best possible combination of subarea, PT, VT, and variables.
| Region | PT | VT | Variables | CSI | POD | FAR |
| Total | 50 | 60 | Mixing ratio 700, divergence 950, divergence 250, GDI | 0.66 | 0.74 | 0.13 |
| Mixing ratio 700, divergence 950, divergence 200, GDI | ||||||
| Mixing ratio 700, divergence 950, divergence 250, divergence 200, GDI | ||||||
| K Index, divergence 950, divergence 250, Total Totals, GDI, PWAT | ||||||
| K Index, divergence 950, divergence 200, Total Totals, GDI, PWAT | ||||||
| K Index, divergence 950, divergence 250, divergence 200, Total Totals, GDI, PWAT |
PT: precipitation threshold; VT: validation threshold; CSI: critical success index; probability of detection; FAR: false alarm ratio.
3.3 RAMI
The LR for the best combination of variables determined in the previous subsection is defined as the RAMI (Rivas, Anderson-Frey, and McMurdie Index). RAMI can be calculated as follows:
where MR 700 is the mixing ratio of water vapor at 700 hPa in g kg-1, D 950 and D 250 are the divergence at 950 and 250 hPa multiplied by 105 in s-1; and finally, GDI is the Gálvez-Davison Index. The linear regression in Eq. (4) must be expressed as a logistic regression using the result of p in the logit function in the following equation:
where k is the result of the logit function. It transforms p into a number between 0 and 1. Thus, RAMI is multiplied by 100 to obtain a probability of rain:
For operational purposes, we suggest that RAMI must be plotted only in the total area (-3.25º to -7º S, -81.5º to -79.5º W) with color-filled contours every four values equal to or above 60, and with solid black contours for values under 60. Figure 7 depicts the proposed color palette and plot settings for RAMI.
3.4 Validation of RAMI
Now that RAMI has been defined, it must be evaluated against the 20% of the data not used to develop the LR. This data was from the optimal combination determined above, namely, the black region (total area of study), PT of 50, and VT of 60, based on 177 different events.
The validation is performed pixel-by-pixel, in which the LR equation (RAMI) established in the previous subsection is compared at each pixel of each region to the occurrence of precipitation as detected by TRMM or GPM.
One of the challenges of performing a pixel-by-pixel validation is that the ERA5 data has a 0.25º spatial resolution while the TRMM and GPM satellite data have a 0.05º resolution. For this evaluation, the satellite data was shifted to the ERA5 grid points using a nearest-neighbor interpolation technique. Each pixel is evaluated to determine whether it has a value of RAMI greater than or equal to the VT of 60 and whether rain is present or not.
This pixel-by-pixel evaluation is repeated for all events with any predicted rain, consisting of 177 different dates, including rain and non-rainy days. However, days with no prediction of rain on behalf of RAMI were excluded because they yield zeros for the denominator of the statistical metrics (e.g., for POD, the values of a + b in Table IV). Therefore, in Figure 8, only 114 days or events are considered (each date consists of a swath of the TRMM or GPM satellite at a given time). RAMI was calculated for each date and time to compare it against the actual value of rain in the NCP in each pixel. Each value of RAMI was evaluated using metrics of skill such as (POD, FAR, and CSI), following the procedure in section 2.3.
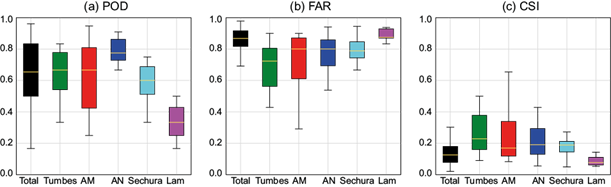
Fig. 8 Pixel-by-pixel validation of RAMI vs. satellite (TRMM and GPM) surface rain shown using boxplots of regions within the NCP (see Fig. 1). (a) Probability of detection (POD), (b) false alarm ratio (FAR), (c) Critical Success Index (CSI). The number of rainy days used is n = 114. (RAMI: Rivas, Anderson-Frey, McMurdie Index; NCP: north coast of Peru.)
POD values in Figure 8a show that the black region (total area of study) presents higher overall skill than the other sub-regions, although the Amotape Mountains (AM) region also has similar values. The Andes region (AN) presents the smallest variability, with values above 0.6, which indicates that it usually presents successful predictions. The northern Andes in the state of Piura are also heavily influenced by El Niño, making precipitation more frequent and intense, which is what RAMI identifies and, thus, yields a high POD. Conversely, the region with the lowest values of POD is the Lambayeque region (Lam). It is the southernmost point of the NCP, which means that convective precipitation on the coast is not as frequent as in the AM or Tumbes regions. Therefore, its prediction is more complex and may indicate that RAMI struggles more to identify rainfall in this region. FAR values (see Fig. 8b) are highest for the total area, which indicates that RAMI tends to overestimate the precipitation forecast in the NCP. More specifically, in the Lam region, which also presents similar values of FAR but with less variability. As it was mentioned, the Lam region is the more complex one to predict precipitation, therefore, most of the forecasts have fallen into false alarms. The AM region presents the lowest values of FAR (under 0.4), meaning false alarms may not be as frequent as in other regions. This could be explained considering that this is a rainy zone because of orographic lifting by the mountains, leading to fewer instances where RAMI identifies rain and it did not occur. The low values of the CSI (see Fig. 8c) in the total area are due to high values of FAR and low values of CSI given by the Lam region. The best values of CSI are achieved in the AM region, which means that RAMI is best at predicting precipitation in this region, followed by the Tumbes region. Again, the Lam region presents the worst performance of all regions, having the lowest values of CSI, which indicates that RAMI may not be too reliable at that location. Overall, RAMI presents good skill in identifying precipitation with relatively few false alarms for the Tumbes, AM, and AN regions. However, it must be used cautiously in the LAM region where the POD is lowest, the FAR is highest, and the CSI has the worst performance.
An example of a graphical contingency table for February 21, 2023, at 03:00 UTC, is presented in Figure 9 in order to illustrate the process behind the pixel-by-pixel validation. This particular date was chosen because it shows good results for the POD, FAR, and CSI metrics, as well as the ease that it presents to understand how the pixel-by-pixel validation was performed for each category in the contingency table (Table IV). Figure 9a shows how RAMI accurately predicts (true positive) 25 pixels of precipitation, but it is apparent from the false positive panel (Fig. 9b) that RAMI tends to overestimate the area of precipitation. False negative values (Fig. 9c) are scarce, which means that RAMI rarely misses no-precipitation forecasts. Lastly, the true negative panel (Fig. 9d) shows 40 pixels of accurately predicted lack of rain, indicating that low values of RAMI accurately highlight regions where precipitation is not expected.
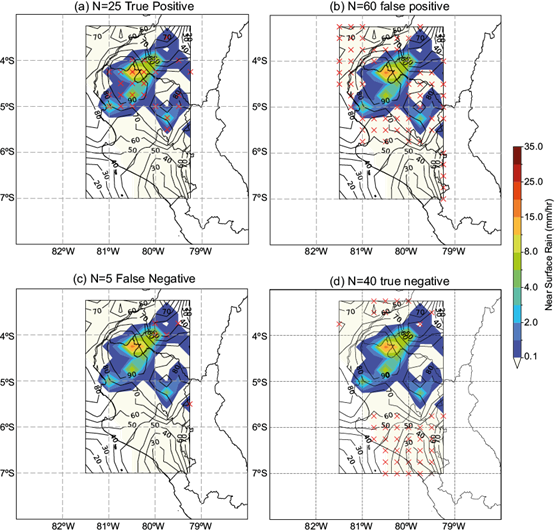
Fig. 9 Graphical representation of the contingency table (Table IV) for February 21, 2017 at 03:00 UTC. (a) True positive grid points depicted by a red “X”. (b) False positive grid points depicted by a red “X”. (c) False negative grid points depicted by a red “X”. (d) True negative grid points depicted by a red “X”. “N” is the number of grid points in each category. Surface rain from GPM is in color-filled contours, and RAMI is in solid black contours. (RAMI: Rivas, Anderson-Frey, McMurdie Index.)
3.5 Comparison with other indices
The final test for RAMI is comparing it against other existing indices that predict heavy rainfall or storms. In order to assess whether RAMI actually is a better-suited index for the NCP, it was compared against the Total Totals index, which indicates thunderstorm potential at values of 45 or higher (Miller, 1972), the K index, which predicts convective potential for values above 20 (George, 1960), and the GDI, which indicates the possibility of heavy rainfall for values above 25 (Gálvez and Davison, 2016). RAMI’s threshold for precipitation occurrence is 60, as determined by the previous steps of this study. Just like in the pixel-by-pixel validation of RAMI, all indices were tested and compared against the TRMM and GPM precipitation estimates using a contingency table, and metrics such as POD, FAR, and CSI were ultimately calculated.
This comparison was also performed on the remaining 20% of the data saved for validation. Figure 10a shows all POD metrics for all indices. The K index does not have a boxplot since it over-predicted rain (e.g., it shows values higher than 20 in most of the total area; therefore, it presented a POD of 1 by predicting rain in the total area, even in regions where rain did not occur, which in turn generated the highest values of FAR). All other indices have significant spread in their POD values, spanning from ~0.5 to > 0.9 for the GDI, from ~0.2 to > 0.9 for RAMI, and the larger spread for the Total Totals index with the lowest performance in POD. RAMI has a median close to 0.8 and more spread than GDI, with the Total Totals index far behind. The latter has the lowest distribution values of FAR compared to other indices (Fig 10b); nonetheless, all indices overestimate precipitation (K presents the highest FAR values due to an over-prediction in the total area). Figure 10c presents the CSI, where all indices present low values, with a median below 0.2. The index with the highest median values is the Total Totals index, with RAMI and GDI close behind. Since RAMI contains the GDI, it is relevant to confirm that it constitutes an improvement; indeed, the GDI has slightly lower values of CSI on average than RAMI.
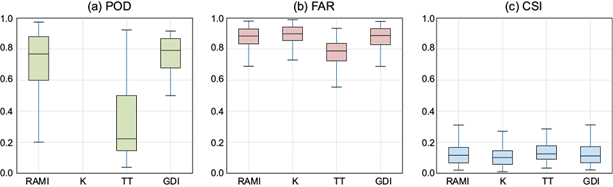
Fig. 10 Pixel-by-pixel validation of multiple indices (RAMI, K index [K], Total Totals Index [TT] and GDI) vs. satellite (TRMM and GPM) surface rain. (a) Probability of detection (POD), (b) false alarm ratio (FAR), (c) Critical Success Index (CSI). (RAMI: Rivas, Anderson-Frey, McMurdie Index; GDI: Gálvez-Davison Index).
Since RAMI performs similarly to other conventional indices, it is safe to say that it is a valid tool to identify precipitation in the NCP. There is potential for RAMI to be a forecasting tool with an adequate evaluation using forecast data. The RAMI presents a few advantages compared to other indices since it highlights physical mechanisms that are important contributors to rainfall in the NCP. For example, it incorporates upper-level divergence (250 hPa) and low-level convergence (950 hPa), which are key factors for mesoscale convective systems (MCS) development.
3.6 Case study
After determining that RAMI performs similarly to other stability indices, we tested it with a storm case study in the NCP. A coastal El Niño developed in the late austral summer of 2023. SST anomalies of +2.5 ºC in March developed into even stronger +4 ºC in April in the Niño 1+2 region, off the coast of the NCP. These conditions facilitated the formation of multiple convective systems, one of which was analyzed using RAMI.
The case occurred on April 15, 2023, between 03:00 and 06:00 UTC, when RAMI successfully identified an MCS in the Amotape mountains due to the high mixing ratio at 700 hPa and the presence of divergence aloft and convergence in the low levels. A comparison between an IR satellite image, a 24-hour rain gauge interpolated data, and the RAMI is presented in Figure 11.
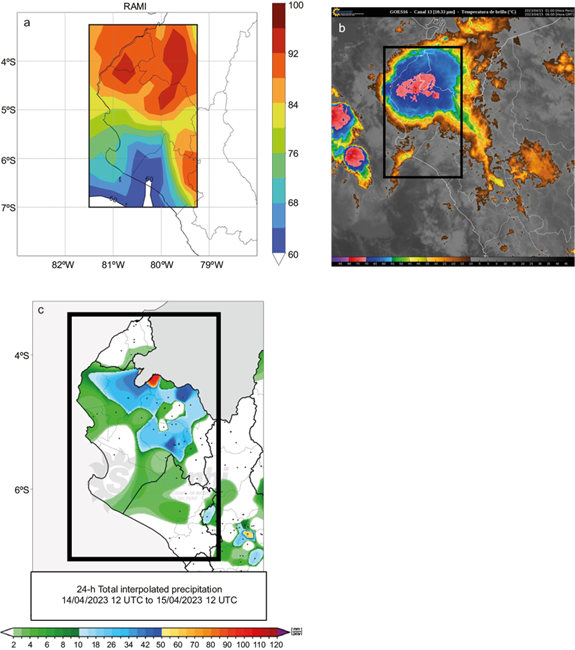
Fig. 11 (a) RAMI (ERA5) in the NCP. (b) IR satellite image from SENAMHI, April 15, 2023 at 06:00 UTC. (c) 24-h total precipitation interpolated from SENAMHI’s rain gauge network for the period April 14-15, 2023 at 12:00 UTC. Black dots represent the location of rain gauges used. (RAMI: Rivas, Anderson-Frey, McMurdie Index; SENHAMI: Servicio Nacional de Meteorología e Hidrología del Perú.)
Comparing RAMI (Fig 11a) versus the IR image (Fig 11b) shows that the highest values of RAMI (above 84) are precisely where a convective system develops around the AM region. The area where precipitation is expected (RAMI values above 60) is much broader than the convective systems present in the IR image. This behavior is consistent with the high values of FAR found in section 3.5.
The RAMI versus interpolated precipitation data (Fig 11c) showed that the good POD values from section 3.5 are due to RAMI identifying correctly where rain developed, in this case, around the AM region. However, there are also regions where rain was not present, and RAMI suggests the presence of rain in the states of Tumbes and Lambayeque (see Fig. 1). This further confirms our results from section 3.5, where the Lam sub-region presents a high rate of false alarm while in the rest of the sub-regions, the RAMI performs well.
4. Conclusions
The LR process used in this study resulted in the best combination of meteorological variables to be chosen for rain diagnosis in the NCP region, eliminating candidate predictors with the lowest odds ratio correlation and emphasizing the ideal combination of region or total area, PT, VT, and predictor variables for precipitation prediction. The choice of the complete area of study (black color box) shows that using the total area of study is more skillful than applying to smaller regions. The PT of 60 mm per region in the study area suggests that the RAMI will be more accurate when the total amount of precipitation in the black box (the entire study area) is equal to or above 60 mm. The selected meteorological variables for the RAMI are consistent with physical mechanisms found by Quispe (2018) and Aliaga-Nestares et al. (2022), whose description of the circulation patterns in different atmospheric levels during El Niño highlight the same essential variables: divergence at 950 hPa for the ITCZ second band detection, mixing ratio at 700 hPa for moisture advection, and divergence at 250 hPa for detecting the influence of the diffluence aloft provided by an anticyclone dipole. Finally, RAMI also considers the GDI, which already includes the thermodynamic profile of the atmosphere.
When compared against other indices, RAMI still performs well, with a decent distribution of POD and comparable skill for FAR and CSI. A case study showed that RAMI does identify regions where convective systems developed, but it also shows that RAMI’s FAR or false alarms may be present in regions such as the Lam where RAMI had lower success.
The RAMI index was developed using the ERA5, a reanalysis product. This allowed the identification of the important processes that contribute to the formation of significant rainfall in the NCP during the warm season, namely upper-level divergence, low-level convergence, mid-level moisture, and column buoyancy, as indicated by the GDI. However, this study did not test whether this combination of predictors would be successful if model forecast grids (such as those available from ECMWF or GFS model forecasts) were used to calculate RAMI and, therefore, be used to predict the potential for rainfall in the NCP. Future studies, where different forecast models and lead times are tested as input fields, will position RAMI as a new tool for rainfall prediction.











 nueva página del texto (beta)
nueva página del texto (beta)






