1 Introduction
Buildings are typical civil structures common in every city around the world. They are subjected to stress mainly due to the lateral loads caused by exogenous forces, such as wind or earthquakes. Currently, structural designs of buildings attempt to achieve a reduction of weight and an increase of slenderness, using high-strength materials or exploiting mechanical properties.
This assures an increase in the building height, with a decent performance in terms of mechanical deflection. In structural engineering three main types of buildings are considered: steel buildings, reinforced concrete buildings and composite buildings [1].
Many tall buildings are built using a combination of the materials mentioned in the previous classification. This is done to have better damping ratios in the overall structure, which reduces the lateral movement of the building affected by the excitation induced by wind loads or earthquakes. In particular, a building can be excited at the base by earthquake forces, causing a movement of all the elements of the structure including the natural frequencies of the building.
This could increase the probabilities of structural damage or even the collapse of the overall structure. Recently, there have been some interesting advances in the development and application of smart materials in the area of civil engineering. These materials are used mainly in bridges and buildings to mitigate problems related with the lateral movements of the structure, contributing to reduce serious problems like auto-excitation of the structure caused by the resonance frequencies of the building. In particular, implementation of piezoelectric stack actuators (PZT) in civil engineering is a decent alternative to monitor and measure the movement or damage of buildings, when they are excited by exogenous forces. Some works are related with the applications of PZT devices as sensors, using three schemes to evaluate the damages in concrete civil structures.
Basically, this PZT stack actuators are mounted on steel bars of reinforced concrete, included inside the concrete mass and concrete surfaces of the construction [2]. There are also some works related with experimental applications of the PZT actuators. For instance [3], presented a civil structure consisting of a four-story building with a total weight of 2000 kg and a height of about 3.7 m. The authors considered PZT actuators mounted on the H-section steel of each floor, including the use of PZT actuators to provide the bending moment to the columns in the overall system. The active control
In recent years, the technological advances of PZT actuators are so notable that it is possible to find actuators able to move high loads of several tons, in particular the PZT actuators manufactured with high voltage ceramics designed with larger cross-sections of civil structures [4].
The use of modal control schemes for active vibration control is an interesting area of Experimental Modal Analysis (EMA), being of great interest the topic of Operational Modal Analysis (OMA). For instance, some works are related with the application of modal control to attenuate vibrations in a building-like structure using Positive Position Feedback (PPF), combined with Sliding Mode Control (SMC), perturbed at the base by harmonic external forces [5, 9]. The authors show experimental results including an extension of PPF control through a Multiple Positive Position Feedback (MPPF).
The remainder of this paper proceeds as follows. Section 2, presents a preliminary analysis of the platform-setup used with the PZT actuator, describing their mechanical characteristics and interfaces. In this section the authors present a simplified mathematical model of the system and an experimental modal analysis, which shows us the first three resonance frequencies of the building-like structure. Section 3, presents the design of the PPF control scheme, establishing the matrix of stability
2 Fundamental Study
The application of structural control for civil engineering to reduce the displacements of the structures due to vibrations when the overall system is excited at the base by external forces can be implemented using one of three typical methodologies, these are known as: passive, semi-active and active vibration control [17, 18]. In this paper, our goal is to show the advantages of active vibration control using a PZT actuator mounted on the column of a building-like structure.
The objective is to reduce the vibrations in several resonant frequencies of the system using the feedback of a sensor placed at a specific section of the structure. In general, adding an actuator will increase the degrees of freedom of the original system, but it can substantially improve the stability of the structure in closed-loop.
2.1 Building-Like Structure using a Smart Actuator Mounted on a Column
Figure 1, shows the experimental setup, which consists of a building model with three-floors, with a height of 450 mm and a rectangular base of 150 × 100 mm2, with a distance between floors of approximately 150 mm. The building-like structure is composed of an aluminum alloy considering an equivalent stiffness
The base or ground borne of the structure is perturbed through external forces applied using an electromagnetic shaker manufactured by Labworks® model ET-139. This rectangular base is mounted over a mechanical rail supported by a set of viscous ball bearings which allows limited lateral movements of the structure.
The electromagnetic shaker allows working with harmonic components of frequencies between 0 to 120 Hz and is controlled via a linear power amplifier manufactured by Labworks® model PA-138. The response and force applied by the electromagnetic shaker to the structure is measured through the impedance head placed at the stinger of the shaker using a cable connected to the NI-CompactDAQ data acquisition system of National Instruments®. This system is integrated with a NI-DAQ-9172 chassis and a NI-9133 module to feedback information of the accelerometers mounted in the floors of the structure. The NI-CompactDAQ is connected via USB to a computer using software programmed in Labview® and an external interface with Matlab/Simulink® associated to a Sensoray® card running Windows 7®.
2.2 PZT Actuator
Figure 2, shows the PZT actuator used in the experimental setup manufactured by Dynamic Structures & Materials® model FPA-0500E P-1036-150-SS-1M3 110, which consists of a mechanical arrangement with springs, which is used to increase the longitudinal motion from the transversal PZT material expansion. The electrical characteristics of the piezoelectric actuator are given in Table 1. The voltage control of the device is carried out through the interface with a Sensoray® card, establishing the implementation of active schemes of control in the building-like structure. The active control force from the PZT actuator is applied directly to the first floor of the structure to reduce or minimize the vibrations at the third floor of the structure, establishing a scheme of control for an under-actuated system.

Fig. 2 PZT actuator model FPA-0500E P-1036-150-SS-1M3 110 manufactured by the Dynamic Structures & Materials®
Table 1 Fundamental characteristics of the PZT actuator
| Parameters | Values |
|---|---|
| Maximum displacement |
|
| Equivalent stiffness |
|
| m (unloaded) |
|
| Resonant frequency | 440 Hz |
| Blocking force | 375 N |
| Operation voltage | -30 to +150 V |
| External control input | -2 to 8 V |
| Restrictive voltage of physical limits |
|
2.3 Analytical Model
In order to analyze the PZT mounted in one beam-column of the first floor of the system, we show in Figure 3, a simplified model of the building-like structure excited at the base by an external force.
The simplified mathematical model of the system is represented as follows:
where
The mass, damping and stiffness matrices for the building-like structure shown in Figure 3 are given by:
In particular, the damping matrix can be expressed in terms of the Rayleigh or proportional damping, which are related with the mass and stiffness matrices expressed as
In a PZT actuator the equivalent stiffness
Therefore, the PZT actuator can be used in the implementation of several schemes of control without affecting the dynamics of the experimental setup with an axial force
2.4 Modal Analysis
In this section we present a study to obtain the experimental resonant frequencies of the structure considering a harmonic external force at the rectangular base of the system. This force is generated using an electromagnetic shaker in an interval between 0 to 60 Hz. The experimental Frequency Response Function (FRF) is studied using the Peak Picking method (for more details see [6]).
In Figure 4, we show the experimental frequency response of the structure, specifically the three dominant modes of the system. In this study we have interest in the lateral displacement of the structure, computed using information provided by the accelerometer placed on the third floor of the system.
A comparative analysis of the resonant frequencies in numerical and experimental form of the building-like structure is presented in Table 2. Table 2 allows us to validate the simplified mathematical model used to represent the building-like structure, which shows a minimal variation between the first three principal resonant frequencies of the system.
3 Design of the Controller
For the implementation of modal control such as PPF, it is necessary to establish a relationship between the resonant frequencies of the system and the suppression frequency designed in the controller.
This control scheme adds an additional degree-of-freedom to the dynamics of the system in close-loop, which is known as a virtual passive absorber or second order low-pass filter.
Basically, this control considers the values of the natural frequency to minimize
The values of the parameters in this modal control are obtained from experimental analysis, which is useful for many researchers and engineers in structural control. In particular, the methodology for the building-like structure uses the position feedback of the third floor to attenuate the amplitude of the resonant frequencies in terms of the lateral displacements of the overall structure.
To tune the parameters of the controller we use an empirical methodology considering a specific damping factor
A general schematic diagram of the active control and PPF controller are shown in Figure 5 and 6.
A simplified mathematical model of the building-like structure with the PZT actuator and the input control in terms of PPF, when excited in the rectangle base by harmonic external forces, is expressed as
with
The PPF control law for the three dominant modes of the structure considering the action of the PZT actuator is expressed as:
with
with
The secondary virtual system (passive absorber) described in Equation (6) is coupled to the primary system (building-like structure) through expression
A compact matrix form of the closed-loop system is given by:
The matrix
4 Vibration Control Experiment
The experimental setup was tested with harmonic frequencies from 0 to 60 Hz. Figure 7 and 8, respectively show the components of force and acceleration applied at the rectangular base, which are measured using the impedance head of the shaker.
The experimental response of the system applying the active vibration PPF control is shown in Figure 9, where we can observe the control effort and frequency response in terms of the displacement, tuning the PPF control to reduce or minimize the first modal resonant frequency of the building-like structure. The parameters of control was selected as
Finally, we can observe in Figure 10 the time response of the system in terms of the horizontal displacement.
Generally, in civil structures the maximum movements of a building excited at the base occurs at the top floor. Therefore, we show the analysis and response of the experimental response only at the third floor of the structure, which is partially reduced on the lateral displacement as observed in Figures 9 and 10.
The experimental response of the system can be improved using a better method of tuning for the parameters of the controller, which is possible through optimization methods. In particular, PPF control is a technique very useful in experimental form due to the ease of implementation and stability.
The drawback is that it is very complicated to obtain an acceptable tuning of the control parameters for this controller [13]. In particular the parameters for the gain and damping ratio in the filter have a strong relation and need fine tuning [13, 14]. Methods to help tune this type of modal control can be useful in practical and experimental applications of civil engineering for many types of systems [13].
For instance, the method described in [14] can be a slow process to obtain a group of tuned parameters for the controller. Some authors propose a fuzzy gain tuner to tune the gain in the PPF control and reduce the initial overshoot with quick vibration suppression in a long composite I-beam with piezoceramics patch sensors and actuators [15].
Finally, there are works related with implementation of meta-heuristic algorithms to optimize the controller using a single objective function by minimizing the mean square error of the observed vibration mode of a flexible beam system. In such methods, the control design does not require knowledge of the input/output characteristics of the overall structure [16].
5 Optimization in the Gains of PPF Control
In this work, we consider the integrated absolute tracking error as the objective
where
5.1 Differential Evolution Method
The method used to perform the optimization is Differential Evolution (DE) [10], which is a well-known metaheuristic for real valued black-box optimization, together with the Interior Point Algorithm [11], (this method comes within the fmincon function in Matlab®). In particular, we used the DE/rand/1/bin version implemented in Matlab® (the source code was taken from [12]).
This method consists in the initialization of a random population of 𝑛 individuals. DE uses two operations to generate new solutions. The first operation consists in a mutation process, which estimates
where
where
The parameters used for the DE method are given in Table 3.
Table 3 Parameters of the DE method
| Parameters | Values |
|---|---|
| Population size |
|
| Number of estimation |
|
| CR |
|
| F |
|
| Simulation time |
|
It is important to observe that DE was used to estimate a good initial solution. The best solution given by DE was then used as the initial point for the Interior Point Algorithm with
5.2 Numerical Response of the PPF Control
The numerical response of the system applying the active vibration control with the optimization method DE is shown in Figure 11, where the movement of the system is reduced significantly using as feedback the position of the third floor.
Figure 12, shows the control effort and frequency response in terms of the displacement, tuning the PPF control to reduce the first modal resonant frequency of the building-like structure. The parameters of control delivered by DE with the Interior Point Algorithm are
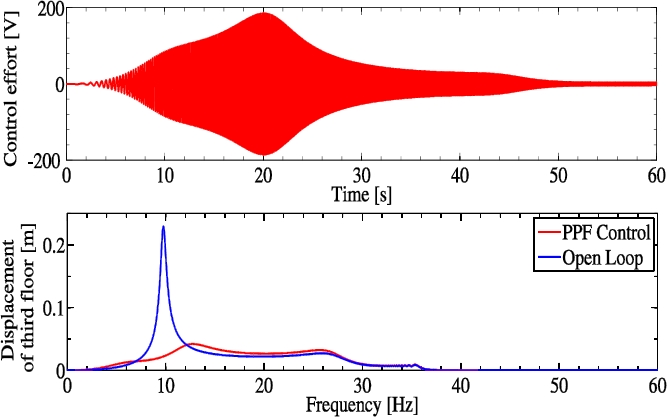
Fig. 12 Displacement of the third floor of the building-like structure using the optimization methods
6 Conclusions
This paper presents a particular case of smart materials implemented in civil structures like buildings, using a PZT stack actuator. The active vibration control is a particular approach considered to reduce movements of the structures when they are perturbed at the base by exogenous forces. An experimental setup is presented, which consists in a building-like structure of three stories excited at the base by an electromagnetic shaker.
The active control scheme is a PPF, using the non-allocated sensor-actuator feedback the displacement of the third floor of the building-like structure. The experimental response of the overall system is attenuated up to 37% employing acceptable control efforts of the PZT actuator. Finally, an optimization analysis for the parameters of the PPF control is presented using metaheuristic methods and a local search, in particular DE and the Interior Point Algorithm.
The numerical results of the controller with optimization are shown to reduce the movement of the building-like structure by around 97%, with a control effort allowed by a PZT stack actuator.
For future works we consider the implementation of the optimized parameters obtained in the experimental platform of the building-like structure and validated by numerical simulations.











 nueva página del texto (beta)
nueva página del texto (beta)












