1. Introducción

Una nueva clase de conjuntos lógicos difusos de mayor orden denominados tipo-2, fueron introducidos por Zadeh en 1975 como una extensión de los conjuntos difusos ordinarios [¹, ²] (tipo-1). Tales conjuntos pueden manejar las incertidumbres presentes en los sistemas debido a que sus grados de pertenencia son así mismos conjuntos difusos tipo-1.

Una justificación para el uso de conjuntos difusos de tipo-2 es la incertidumbre que puede existir en los sistemas en los que se aplican conjuntos difusos tipo-1. Esta incertidumbre puede presentarse en distintas formas [³]: reglas con diferente significado para diferentes expertos; consecuentes que difieren para reglas idénticas según diferentes expertos; ruido presente en los en los transductores de medición de las variables físicas o en la naturaleza misma de las variables involucradas y diferencias entre el modelo matemático y el sistema real. Así, se puede pensar en los conjuntos difusos tipo-1, como conjuntos difusos con aproximación de primer orden para la representación de la incertidumbre. Siendo de esta forma, los conjuntos difusos tipo-2 una aproximación de segundo orden de la incertidumbre presente en situaciones del mundo real [⁴].

Por otra parte, actualmente las máquinas de corriente directa (CD), no son ampliamente utilizadas como años atrás. Los generadores de CD han sido reemplazados en la actualidad por elementos de estado sólido. Sin embargo, aun los motores de CD aunque a bajas potencias [¹²,¹³], son utilizables en áreas de la electrónica industrial (para control de velocidad y posicionamiento), robótica, automotriz, aplicaciones en grúas, elevadores e industria en general. Esto debido a sus características de torque-velocidad, presentes en las diversas configuraciones del motor CD [¹⁴].

Para el control de los motores de CD, los controladores lógicos difusos tipo-1 han mostrado ser superiores en varios aspectos a los tradicionales controladores P, PI, PID. Entre ellos se puede mencionar menor sobretiro, robustez, estabilidad, entre otros. [¹⁰, ¹⁵, ¹⁶, ¹⁷, ¹⁹, ²⁰, ²⁷] Por esta razón los controladores convencionales no son considerados en este trabajo, que se concentra en el estudio comparativo ante grandes disturbios deterministas y estocásticos, entre controladores difusos tipo-1 y tipo-2 como en [¹¹, ¹⁸, ²², ²⁴, ²⁵]. No obstante los controladores convencionales PID pueden trabajar en conjunto con los controladores difusos, y aprovechar su sistema de inferencia mediante el razonamiento aproximado para su propia sintonización [²⁰, ²¹].

La implementación de los sistemas difusos tipo-1 se ha realizado satisfactoriamente en dispositivos lógicos programables [²⁹]. Incluso algunas metodologías basadas en amplificadores operacionales han sido presentadas para la implementación de los procesos de defusificación y dedefusificación de sistemas difusos tipo-1 [²⁸].

Por su parte, la implementación de los controladores difusos tipo-2 requiere de grandes recursos computacionales [²⁵]. Las diferentes alternativas para su implementación en computadoras personales, así como en dispositivos programables es un tópico actual de investigación [²⁵,³⁰,³¹,³²], que merecen investigaciones de mayor tamaño y atención científica y computacional.

Los resultados en este trabajo se presentan a nivel simulación como en [¹¹, ¹⁸, ²², ²⁴, ²⁵, ²⁶]. Cabe mencionar que las pruebas de simulación permiten probar controladores en etapa experimental y predecir comportamientos, lo que ayuda al estudio de factibilidad del método propuesto.

En lo que respecta a controladores tipo-2 frente a controladores difusos tipo-1, se han mostrado resultados satisfactorios en [¹¹, ¹⁸, ²², ²⁴, ²⁵]. En [¹⁸] se analiza un controlador difuso tipo-2 en intervalos frente a un control difuso tipo-1 para un pequeño servomotor de baja potencia, ante un escalón unitario. Pequeños cambios de carga con y sin incertidumbre, utilizando software comercial.

En [²²], se estudia un controlador difuso PI tipo-2 frente a un control difuso tipo-1. El autor propone funciones de membresía tipo diamante para sus universos de entrada. Los controladores se aplican únicamente a un sistema de primer orden. Se muestran pruebas ante cambios tipo escalón, obteniendo resultados contundentes cuando la incertidumbre en dichos conjuntos difusos aumenta.

Por su parte los trabajos [²⁴, ²⁵] son similares al presente.

Aunque en estos se controla la velocidad de un motor DC y se analizan los controladores tipo-1 y 2 ante pequeños disturbios y señales escalón. Los pequeños disturbios se modelan como cambios pequeños en la referencia de velocidad o carga mecánica en el eje del motor. En este trabajo se estudia el controlador difuso tipo-2 sujeto a disturbios grandes. Lo cual permite llevar al controlador a situaciones de no linealidad, extremas no convencionales y zonas de posible inestabilidad, para evaluar el comportamiento. Además, también se añade ruido a la señal de carga mecánica aplicada al eje del motor.

Se utilizan controles difusos para el control de motores de CD, ya que se presentan incertidumbres en los parámetros del motor debidas a variaciones naturales y nolinealidades; así como ruidos en las señales de alimentación y medición; además los grandes disturbios excitan situaciones nolineales y posiblemente inestables. Especialmente los controles difusos tipo-2 modelan la incertidumbre como una aproximación de segundo orden [⁴] y con mayor eficiencia computacional.

Este trabajo es continuación de un trabajo previo [¹¹]. En el cual se analizan los controladores difusos tipo-1 y tipo-2 para la regulación de velocidad de un motor CD con excitación separada utilizando el algoritmo convencional de Karnick & Mendel y se analizan casos a pequeños disturbios.

La aportación de este artículo consiste en exponer el control difuso en intervalos tipo-2 ante grandes disturbios con y sin carga estocástica. La carga estocástica se modela como cambios continuos del valor de carga alrededor de una media. Por lo que se tiene una señal de disturbio grande con ruido. Esto permite exponer al controlador ante situaciones de no linealidad, situaciones extremas no convencionales y posible inestabilidad. Ya que cuando un sistema se somete a un disturbo grande, su respuesta es no lineal, a diferencia de los problemas con señales de pequeños disturbios, donde la respuesta es lineal [¹⁸, ²², ²⁴, ²⁵].

Se propone la arquitectura del control tipo-2 con el algoritmo mejorado de Karnik & Mendel (EKM por sus siglas en inglés), ante grandes disturbios. Se realiza la comparación entre ambos algoritmo Karnik & Mendel y Karnik & Mendel mejorado. Siendo este último más eficiente en tiempo de ejecución, en base a los resultados que se muestran en el apéndice 4.2. Los algoritmos de control se desarrollaron en lenguaje Matlab. Esto motiva a futuros trabajos de implementación en dispositivos programables.

El modelo utilizado para las simulaciones es el modelo no lineal de un motor de corriente directa de 5 HP, incluyendo el limitador del voltaje de armadura. El disturbio grande es un incremento del 100 % en el par de carga. Es decir, una fuerza externa que tiende a frenar al motor.

La sintonización del controlador tipo-2 se realiza a partir de un control tipo-1 sintonizado. Ambos controladores mantienen el mismo dominio en sus universos difusos de entrada y las mismas reglas difusas. La medición del desempeño se realiza mediante la cuantificación del error a partir de índices de desempeño ISE, IAE e ITAE. Los resultados muestran la ventaja del controlador tipo-2 ante disturbios grandes con y sin carga estocástica. Esto se debe a un mejor manejo de las incertidumbres, por parte de los conjuntos difusos tipo-2 y al comportamiento no lineal del controlador tipo-2. Finalmente estos resultados permiten concluir la robustez de los controladores difusos que son capaces de mantener la estabilidad, incluso cuando son expuestos en situaciones de no linealidad por disturbios grandes deterministas y estocásticos.

2. Arquitectura de un controlador lógico difuso tipo-2

Un controlador lógico difuso que utilice al menos un conjunto difuso caracterizado por una función de membresía tipo-2, es llamado controlador lógico difuso general tipo 2 [⁵]. Este último se representa mediante A˜ y en su función de membresía intervienen tres dimensiones de la forma (x,u,μA˜(x,u)), en donde x∈X, u∈Jx, y 0≤μA˜(u,x)≤1. x es la variable de entrada mapeada. En este caso X=[e Δe] (definido en (5)), es un vector de dos dimensiones que incluye el error de la velocidad del motor y el cambio del error, ambas en rpm. u es el grado de membresía primario, mientras que μA˜(x,u) se conoce como grado de membresía secundario [⁶]. Así estos conjuntos son más complejos debido a la nueva dimensión en sus grados de pertenencia asociados.

Con lo que se tienen sistemas de inferencia y procesos de reducción complejos y tardados.

Cuando todos los valores de los grados de membresía secundarios son unitarios, el conjunto difuso tipo-2 se reduce a un caso especial denominado, conjunto difuso tipo-2 en intervalos [⁷]. De esta forma se tiene un controlador intervalo difuso tipo-2. La estructura del controlador es mostrada en la figura 1 [²³].

Fig. 1 Elementos del controlador difuso tipo-2 en intervalos 

Los controladores utilizados son denominados PI tipo-1 y PI tipo-2. La salida Y (Δva), en ambos controladores es el incremento del voltaje de armadura (ver (6)) y es de tipo incremental. Es decir, el incremento positivo o negativo de su variable de salida, dependerá de sus valores actuales.

2.2. Sistema de inferencia para un sistema difuso tipo-2 en intervalos

Considerando un sistema lógico difuso con p entradas x1∈X1, x2∈X2, …, xP∈XP, y una sola salida. El cual utiliza reglas difusas de tipo SI-ENTONCES, las cuales son de la forma siguiente:

Rl:Six1 es A˜1l "y" x2 es A˜2l "y" …… "y" xp es A˜pl entonces y es C˜l. (4)

Esta estructura de regla representa una relación difusa tipo-2, entre el espacio de las variables de entrada y la variable de salida. En donde A˜1l, expresa un conjunto difuso tipo-2, en el universo de discurso de la variable x1. El subíndice l hace referencia a la l-ésima regla difusa.

Mientras que C˜l se refiere al conjunto de salida difuso tipo-2 para la l-ésima regla. Es decir, es la parte consecuente de una regla difusa. Para nuestro caso en particular C˜l serán los centros de membresía de los conjuntos difusos en el universo de salida del controlador, figura 8.

Fig. 2 Conjunto difuso tipo-2 en intervalos 

Fig. 3 Sistema de inferencia para una regla con consecuentes y antecedentes intervalo tipo 2 

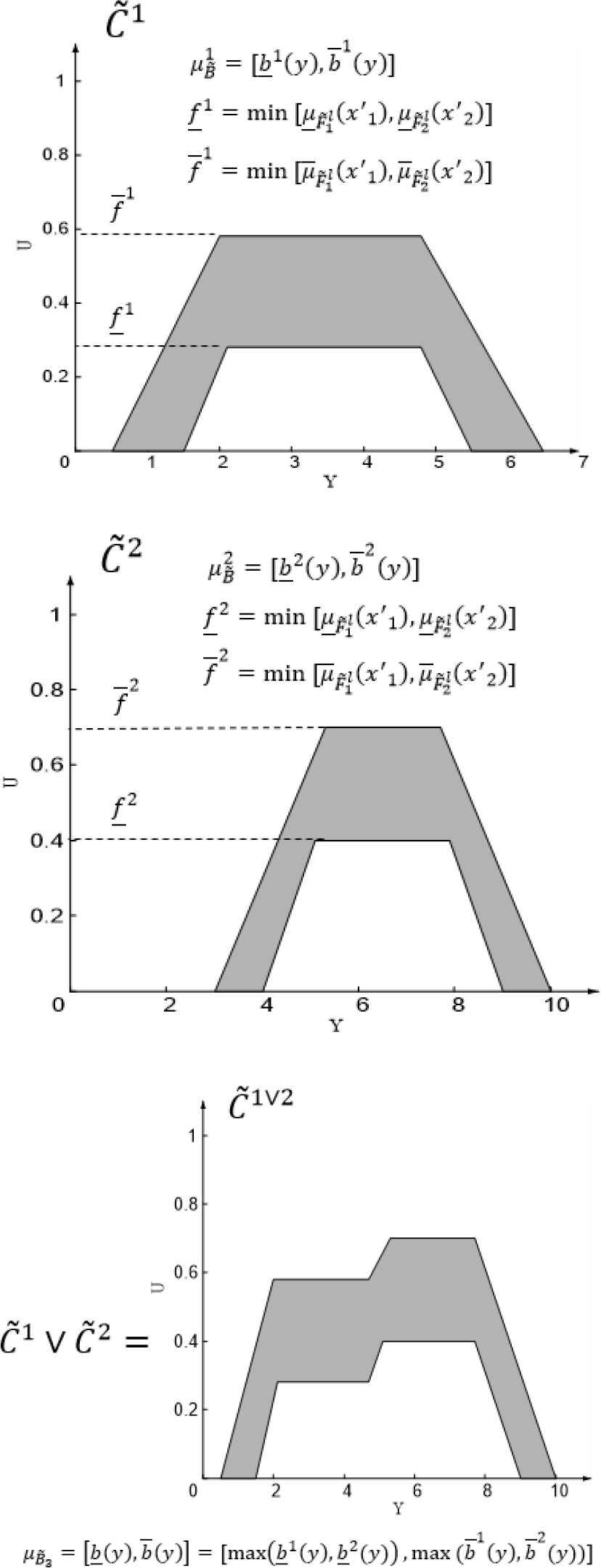
Fig. 4 Sistema de inferencia para dos reglas difusas, con conjuntos consecuentes tipo-2, ∨ indica máximo 

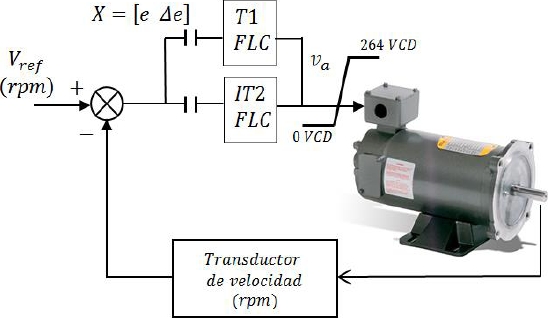
Fig. 5 Esquema de la aplicación de los controladores difusos tipo-1 y 2 sobre el control de velocidad del motor de CD 

Fig. 6 Universos de entrada del controlador tipo 2: (a) error, (b) cambio del error 

Fig. 7 Universos de entrada del controlador tipo 1: (a) error, (b) cambio del error 

Fig. 8 Barras de salida para ambos controladores 

La estructura de las reglas tiene la misma forma que las reglas en un sistema lógico difuso tradicional. Con la particularidad de que se utilizan conjuntos difusos tipo-2.

El análisis en forma gráfica del sistema de inferencia para una sola regla difusa se muestra en las tablas 1 y 2, donde el grado de membresía inferior LMF y superior UMF del conjunto de salida C˜1∨2, resultado de la unión de C˜1 y C˜2. Además LMF y UMF del conjunto difuso tipo-2 en intervalos de salida, son determinados mediante el operador máximo [⁷]. Para el caso de activación de dos reglas difusas se presenta la Tabla 2.

Tabla 1 Algoritmo Mejorado de Karnik & Mendel para el cálculo de yl. 

Cálculo de yl

1.- Hacer discreto cada conjunto de salida en N puntos xi es decir {x¯1,…,x¯N}. Tal que x¯1<x¯2<⋯x¯N

2.- Hacer k=N/2.4 (redondear al entero más cercano).

3.- Calcular a=Σi=1kx¯iμ¯B˜(xi)+Σi=k+1Nx¯iμ¯B˜(xi)

4.- Calcular b=Σi=1kμ¯B˜(xi)+Σi=k+1Nμ¯B˜(xi)

5.- Hallar k′ tal que xk′≤a/b<xk′+1

6.- Mientras k′≠k hacer:

7.- Hacer s=signo(k′−k)

8.- Actualiza

a←a+sΣi=min⁡{k,k′}+1max⁡{k,k′}x¯i(μ¯B˜(xi)−μ¯B˜(xi))

9.- Actualiza

b←b+sΣi=min⁡{k,k′}+1max⁡{k,k′}μ¯B˜(xi)−μ¯B˜(xi)

10.- Actualiza k←k′

11.- Hallar k′ tal que xk′≤a/b<xk′+1

12.- Retorna yl=a/b; y L=k

Tabla 2 Algoritmo Mejorado de Karnik & Mendel para el cálculo de yr. 

Cálculo de yr

1.- Hacer discreto cada conjunto de salida en N puntos xi es decir {x1,…,xN}.

Tal que x¯1<x¯2<⋯x¯N

2.- Hacer k=N/1.7 (redondear al entero más cercano).

3.- Calcular a=Σi=1kx¯iμ¯B˜(xi)+Σi=k+1Nx¯iμ¯B˜(xi)

4.- Calcular a=Σi=1kμ¯B˜(xi)+Σi=k+1Nμ¯B˜(xi)

5.-Hallar k′ tal que xk′≤a/b<xk′+1

6.- Mientras k′≠k hacer:

7.- Hacer s=signo(k′−k)

8.- Actualiza

a←a+sΣi=min⁡{k,k′}+1max⁡{k,k′}x¯i(μ¯B˜(xi)−μ¯B˜(xi))

9.- Actualiza

b←b+sΣi=min⁡{k,k′}+1max⁡{k,k′}μ¯B˜(xi)−μ¯B˜(xi)

10.- Actualiza k←k′

11.- Hallar k′ tal que xk′≤a/b<xk′+1

12.- Retorna yr=a/b; y R=k

3. Pruebas y resultados

Las pruebas fueron realizadas considerando el motor de corriente directa operando a valores nominales de placa en lo que respecta a velocidad, potencia, voltaje, corriente de armadura, corriente de campo, y par mecánico de carga según [¹⁰]. Los valores nominales son: 5 HP, voltaje de campo 240 VCD, corriente de campo 1 A, voltaje de armadura 240 VCD, corriente de armadura 39.58 A, velocidad nominal 120.14 red/seg ≈ 1147 rpm y par externo de carga de 29.2 N-m.

El modelo no lineal de la máquina CD operando en régimen motor configuración excitación separada, así como la nomenclatura se muestran en el apéndice 4.1.

Los parámetros del motor CD son:

En [¹¹], se realizaron pruebas a pequeños disturbios. Es decir, pequeños cambios en el par externo de carga mecánica y en la velocidad de referencia a intervalos de tiempo específicos.

El controlador difuso tipo-2 con nueve reglas mostró mejor desempeño que el convencional tipo 1 con 25 reglas. Esto indica que un control difuso tipo-2 con menor conocimiento mostró mejor desempeño. Por lo que aquí se analiza el controlador tipo-2 con el menor número de reglas ante un gran disturbio en el par externo de carga, así como situaciones con y sin incertidumbre. Además, en [¹¹] se utilizó el algoritmo convencional de Karnik & Mendel.

En las presentes simulaciones se ocupó el algoritmo mejorado de Karnik & Mendel presentado en la sección 2.2. En el apéndice 4.2 se muestra como este último es superior a su predecesor Karnik & Mendel convencional, en el número de iteraciones. En todos los casos se compara el desempeño de un controlador difuso PI tipo-1, y un controlador difuso PI tipo-2 en intervalos. El control difuso tipo-1 es del tipo Mandami. Y es similar al utilizado en [¹⁵, ¹⁶, ¹⁷, ¹⁹, ²⁰].

Se utilizan tres funciones de membresía triangulares para ambos universos de discurso de las variables de entrada e y Δe (error y cambio del error respectivamente). La incertidumbre para los conjuntos difusos tipo 2 son: δerror=1, δΔerror=0.01. Las barras de salida y las reglas difusas son idénticas para ambos controladores. Estos parámetros son tomados de las pruebas hechas en [¹¹]. La diferencia en el diseño está en la incertidumbre para los conjuntos difusos tipo-2 así como el algoritmo de reducción de tipo para el procesamiento de la salida del controlador tipo-2.

En el apéndice 4.2 se muestra un menor número de operaciones realizadas por EKM sobre KM. De aquí que el controlador utilizado es más eficiente en tiempo de respuesta que el utilizado en [¹¹].

3.1. Disturbio grande en carga mecánica sin ruido

Se considera al motor operando a valores nominales, simulando un aumento en el par externo de carga mecánica a un valor igual a dos veces del valor nominal. Es decir un ΔTm del 100% sobre el valor nominal. Este disturbio sucede en el primer segundo de simulación con duración de 0.2 segundos. La señal de disturbio es rectangular, figura 10.

Fig. 9 Comportamiento de la velocidad, sin ruido en el par externo de carga 

Fig. 10 Disturbio en la carga sin ruido 

3.2. Disturbio grande en carga mecánica con ruido

Para este caso se considera condiciones de arranque y disturbio similares a 3.1, pero agregando ruido en el par externo de carga mecánica.

Esto se logra mediante la generación de números aleatorios rand con una distribución normal N(0,1).

Para generar el un valor aleatorio C con distribución normal con media en A y una desviación estándar B, se tiene:

C=A+B∗rand. (7)

Entonces, para generar el ruido en el par externo de carga con una desviación estándar del 3% del valor actual del par (con lo que se tendrá una banda de variación en ≈ ±9%), que se realiza en cada paso de integración:

Tm=Tm_ideal+(Tmideal∗0.03)∗rand, (8)

donde Tmideal tiene un valor constante para determinados intervalos de tiempo durante la simulación:

Tm_ideal{29.2;     0≤t<158.4; 1≤t≤1.0229.2;     t≥1.02}. (9)

Tm_ideal=58.4, es el incremento del 100% del valor del par en plena carga, para la simulación del disturbio. El resultado es mostrado en la figura 17.

Fig. 11 Comportamiento de la corriente de armadura, sin ruido en el par externo de carga 

Fig. 12 Voltaje de armadura sin ruido en el par externo de carga 

Fig. 13 Diagrama de fase de los controladores, sin ruido en el par externo de carga 

Fig. 14 Índices del error, sin ruido en el par externo de carga 

Fig. 15 Comportamiento de la velocidad, con ruido en el par externo de carga 

Fig. 16 Disturbio en la carga, con ruido 

Fig. 17 Comportamiento de la corriente de armadura, con ruido en el par externo de carga 

3. Conclusiones

Los controladores difusos son poderosas herramientas de control no convencional para la implementación en sistemas de control en sistemas nolineales. El controlador difuso en intervalos PI tipo-2 estudiado en este trabajo muestra mejores resultados en desempeño en la respuesta en el tiempo y en los índices de error, para un gran disturbio en el par externo de carga con y sin ruido, que el PI tipo-1. Esto demuestra la robustez de los controles difusos tipo-1 y tipo-2, cuando el sistema de control es llevado a zonas de no linealidad e inestabilidad. La respuesta no lineal de ambos controladores se puede observar en las figuras 12 y 18.

Fig. 18 Voltaje de armadura con ruido en el par externo de carga 

La distorsión en los diagramas de fase de ambos controladores es el resultado de las incertidumbres añadidas en el disturbio. De estos diagramas es posible notar el desempeño no lineal de ambos controladores para mantener control sobre el sistema.

El control tipo-2 mostró una mejor respuesta dinámica ante un disturbio pequeño en la velocidad de referencia que el control tipo-1.

El algoritmo de reducción de tipo utilizado en este trabajo fue el algoritmo mejorado de Karnik & Mendel.

El cual presenta menor tiempo de ejecución, ya que converge en forma más rápida que el tradicional Karnik & Mendel (Apéndice 4.2). Esta característica es importante para futuras implementaciones de control en tiempo real.

De todas las simulaciones realizadas las funciones de membresía, número de reglas difusas, número de barras de salida y tablas de reglas difusas con las que se obtuvieron los mejores resultados, se muestran en las figuras 6, 7, 8 y tabla 3. Estas son variables comunes para ambos controladores tipo 1 y 2.

El controlador tipo-2 comparado con el tipo-1, requiere, además, la selección del algoritmo de reducción de tipo y la cantidad de incertidumbre de los conjuntos difusos de entrada, para la sintonización. Lo cual si no se tiene mucha experiencia resulta complejo para el diseño del controlador. Se recomienda inicializar el controlador difuso tipo-2 con los resultados sintonizados de un control difuso tipo-1.

Para futuros trabajos se propone la implementación en laboratorio en base a un microcontrolador, ya que se pueden presentar problemas particulares de investigación. debido a que se requiere una buena ingeniería de software por las grandes cantidades de operaciones a realizar [²⁵, ³⁰, ³¹, ³²].

4. Apéndices

4.2 Número de Iteraciones del Algoritmo Karnik & Mendel (KM) y del Algoritmo Mejorado Karnik & Mendel (EKM)

Para las condiciones dadas en 3.1 (condiciones ideales), el comportamiento del controlador difuso tipo-2 operando con KM y EKM es idéntico, es decir ambos algoritmos convergen al mismo resultado para el mismo instante de tiempo de simulación. La principal diferencia radica en el número de iteraciones que ambos algoritmos ocupan para obtener el resultado final.

Ambos algoritmos se ocupan en encontrar los puntos de conmutación yl y yr [⁷, ²³], para luego promediar entre estos puntos. Para el análisis de desempeño, se compara el número de iteraciones que ambos controladores desarrollan durante el tiempo de simulación.

Como puede observarse en las figuras 23 y 24, ambos algoritmos de reducción de tipo utilizan una iteración durante el primer segundo de simulación (estado estacionario). Se tiene un disturbio de 0.2 segundos y de ahí en adelante el algoritmo KM utiliza entre 3 y 4 iteraciones para converger al resultado de yl y yr.

Mientras que el EKM presenta un menor tiempo de ejecución, ya que utiliza siempre una sola iteración para converger al resultado.

Fig. 19 Diagrama de fase de los controladores, con ruido en el par externo de carga 

Fig. 20 Índices del error, con ruido en el par externo de carga 

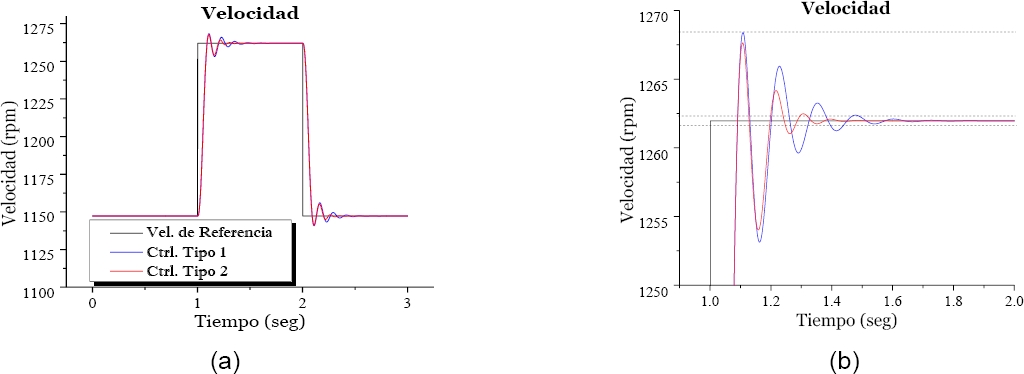
Fig. 21 Respuesta dinámica ante un cambio en la referencia de la velocidad: a) respuesta dinámica; b) acercamiento de la respuesta 

Fig. 22 Circuitos equivalentes del motor DC 

Fig. 23 Número de iteraciones desarrollado por KM y EKM para la obtención de yl  

Fig. 24 Número de iteraciones desarrollado por KM y EKM para la obtención de yr