Introduction
Sound assessments of fishing resources are critical for management (Melnychuk et al., 2017). However, a pervasive challenge is scarcity of data (Hilborn et al., 2020). Often, catch-effort series are used to fit models because catch-per-unit-effort (CPUE) indicates abundance, despite caveats (Harley et al., 2001; Haggarty and King, 2006). However, CPUE may remain high even if abundance decreased; this is known as hyperstability and typically happens when dioecius fish aggregate to reproduce (Erisman et al., 2011).
The gulf corvina (Cynoscion othonopterus) is a marine fish endemic to the gulf of California (henceforth, the gulf), commercially fished within a biosphere reserve under an annual quota regime. Assessing this species remains a challenge because it does not lend itself to standard assessments due to hyperstability, that results in spawning aggregations which increases its vulnerability to fishing. This might indeed be resulting in biased estimates, crucial to allocate quotas.
From January to May, corvina forms spawning aggregations (SA) in shallow (< 50 m) waters at the upper gulf, resulting in increased vulnerability to fishing. Over 4,000 ton per year are taken by ~700 small-scale vessels. Management based on a total annual catch is done since 2012 (Mendívil-Mendoza et al., 2018). Corvina grows relatively fast, reaching maturity in two years (Gherard et al., 2013). An average female lays ~1´670,000 eggs per spawn (Román-Rodríguez, 2000; Cotero-Altamirano et al., 2018), associated with high productivity of the area (Gherard et al., 2013).
Hyperstability challenges stock assessments and management (Mackinson et al., 1997). A good example was the collapse of northern cod (Gadus morhua) stock off Newfoundland and Labrador (Rose and Kulka, 1999). One way to overcome this problem is using ancillary, fisheries-independent information; another desirable way to improve modelling is relaxing assumption of direct proportionality of CPUE and abundance (Ulltang, 1996; Walter and Porch, 2012). The latter can be done by replacing the production function where Y is yield, q is constant catchability, f is fishing effort and B is biomass of the fishing resource. An alternative production function (Cobb and Douglas, 1928) is (i.e., Y/fµ = Bγ) where μ and γ reflect relation between CPUE and abundance (Harley et al., 2001). When µ and γ <1, either yield is affected as effort increases, or catchability increases as biomass decreases, respectively. When both µ and γ = 1, the production function is equivalent to Schaefer’s function, widely used to assess fished stocks. It is also useful to conduct stock reduction analysis (SRA) (Kimura and Tagart, 1982) which, based on annual catches, seeks to solve Baranov’s catch equations system (Baranov, 1918) linked to natural mortality M, biomass, recruitment, and a biomass reduction ratios.
The gulf corvina has high economic value: flesh, swim bladder and gonads are commercialized; this strongly increases market demand. In open access (de facto or de jure) regimes, economic value can stimulate fishing effort and stock depletion to risky levels; this is particularly true for stocks, such as corvina, which form SA. In such cases, bionomic models can provide information useful for management (Pascoe et al., 2016). Some types of models consider age or size structure (Jensen, 1974; Schnute, 1987; Martell et al., 2008; Methot and Wetzel, 2013) which, in comparison to aggregated models, allow more realistic analyses, for example the influence of natural or fishery-induced variability at different ages. Such models are highly demanding in terms of data and information, while biomass-aggregated models are widely used for stock management, particularly in data poor situations (Haddon, 2011). Here, we follow an approach of information theory and test six different model scenarios, all based on the assumption of aggregated biomass. We assess the gulf corvina (henceforth, corvina) through a bionomic evaluation of its fishery using SRA with a Cobb-Douglas function (Hannesson, 1983). This allowed consideration of catchability as a function of stock biomass, hence accounting for hyperstability.
Materials and methods
Annual corvina catch data (1991 to 2019) were obtained from research centers (IMIPAS, CIBNOR) and effort (2013 to 2019) from Mexico’s federal fishing authority (CONAPESCA) (Fig. 1). Effort is mean number of boats operating during a fishing season. Corvina beach price and effort costs were collected through interviews with fishers and by Environmental Defense Fund of Mexico (EDF). All prices refer to year 2019.
The SRA (Kimura and Tagart, 1982) was used to assess the corvina. Data consisted of annual catch series, two estimates of natural mortality rates M = 0.26 and 0.38year-1 (Erisman et al., 2014) and virgin biomass ranging between 15,000 to 30,000 tons. SRA solves n+1 (n = # of years) simultaneous nonlinear equations for catch (Ci), biomass (Bi) and biomass depletion rate (P) observed in n years of fishing:
where, for year i, Fi = instantaneous fishing natural mortality rate, and R=constant recruitment. We used fixed values of M, B1 and P, and solved for R, F1, … , Fn restricting solution to values of B1 and P that intersected virgin biomass (B1), recruitment and exploitation rate (E ̅ = F/(Fi+M) = 0.825; 0.794, 0.858 95% CI) for years 2013 to 2015 (Erisman et al., 2014; 2020). Biomass was then projected after 2019, changing Fi to test catch quota scenarios.
For the bionomic analysis, the Cobb-Douglas function was fitted to annual biomass data (2014-2019) estimated with SRA using M = 0.26, restricted to E ̅ = 2013-2015 = 0.825, and observed catch-effort. Six production function were fitted:
Case 1)
Case 2)
Case 3)
Case 4)
Case 5)
Case 6)
Note that case 6 is Schaefer’s model which could a priori be discarded in the case of corvina, due to hyperstability. However, it was included because in case of being a “loser” model, it should be disregarded in fisheries management decisions. Models were fitted using maximum likelihood assuming lognormal residuals; the “best” model was chosen using the Akaike criterion for small sample size (AICc) (Burnham and Anderson, 2002).
The Cobb-Douglas function was equated to biological SRA yield function and solved for f to estimate fishing effort:
fPEC is equilibrium effort to obtain a sustainable yield, B is biomass in equilibrium.
Total income was obtained multiplying corvina beach price by sustainable biological yield; costs were estimated multiplying cost per unit effort by total effort. Total net income (πt) was obtained subtracting cost income: πt=p[A*fμ Bγ]-cf. Solving for f and equating total net income to zero, effort in economic equilibrium fEEC was estimated as:
fEBE occurs when fPEC = fEEC. Effort for maximum economic yield fMEY was obtained equating the income function to zero and obtaining the first derivative as a function of f:
Results
Stock Reduction Analysis (SRA)
With M = 0.26 y-1, solutions to the catch equation system were found for a biomass decline ratio ≥ 0.24 (Table 1) for constraint E ̅ = 2013-2015 = 0.825 and 0.794; no solutions where possible when E ̅ = 2013-2015 = 0.858. With M = 0.26 and restrictions of E ̅ = 2013-2015, solutions were found for biomass depletion ratio between 0.24-0.276; initial biomass ranged between 19,465-20,814 ton, and annual recruitment 4,444-4,768 ton. With M = 0.38, solutions were limited to biomass depletion rate between 0.330-0.345.
Table 1 Results of the SRA model for gulf corvina (Cynoscion othonopterus) considering two values of annual natural mortality rate (M) restricted to E ̅ 2013-2015.
Tabla 1 Resultados del modelo SRA para curvina golfina (Cynoscion othonopterus) considerando dos valores de tasa de mortalidad natural anual (M) restringida por E ̅ 2013-2015.
| M | P | B1 | E ̅ 2013-2015 | R |
|---|---|---|---|---|
| 0.26 | 0.235 | No solutions | ||
| 0.240 | 19,465 | 0.847 | 4,444 | |
| 0.253 | 20,000 | 0.825 | 4,579 | |
| 0.276 | 20,814 | 0.794 | 4,768 | |
| 0.38 | 0.250 | No solutions | ||
| 0.300 | No solutions | |||
| 0.330 | 14,881 | 0.824 | 4,678 | |
| 0.345 | 15,632 | 0.794 | 4,884 |
Estimates of B1 differed for both M values (Fig. 2A). Final biomass varied slightly regardless of M: 4,500 - 5,700 tons. Current biomass relative to B1 for both M values showed a similar pattern of decline; at the end of the series relative biomass estimates with M = 0.26 were nearly 0.25*B1. Solutions with M = 0.38 suggest declining biomass between 0.33 - 0.345 of B1 (Fig. 2B).
With M = 0.38 y-1 and both restrictions of E ̅ 2013-2015, SRA yielded F estimates higher than with M = 0.26. However, at the end of 2019, with restrictions in either M and E ̅ 2013-2015 resulted in F to vary between 1.5 - 2.7 (Fig. 3), higher than F0.5B1,M 0.26 = 0.35 or F0.5B1, M 0.38 = 0.61. F increased sharply from 2012-2016 and dropped in 2017, coinciding with decreased fishing due to a “payment for not fishing” policy implemented to which most fishers subscribed. The highest F was for 2016, when the largest catch was recorded.
Figure 3 Estimated instantaneous fishing mortality rate of Cynoscion othonopterus at the upper gulf of California from 1991 to 2019. The number above the dashed line is an F value out of scale. Horizontal lines represent the F value required for a constant stock of 0.5K for two values of M.
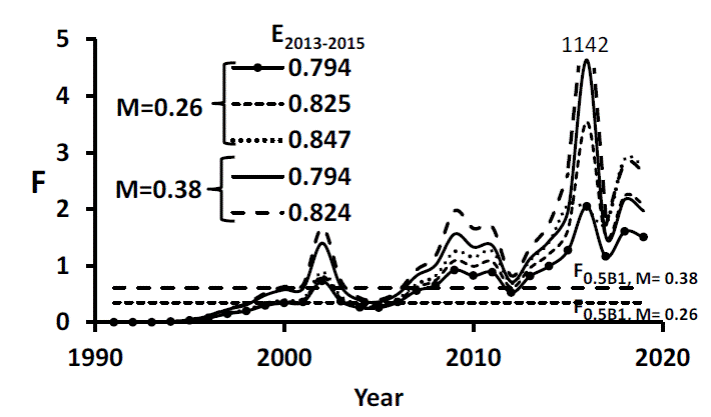
Figure 3 Tasa instantánea de mortalidad por pesca estimada de Cynoscion othonopterus en el alto golfo de California desde 1991 a 2019. El número sobre la línea discontinua es un valor F fuera de escala. Las líneas horizontales representan el valor de F requerido para un stock constante de 0.5K para dos valores de M.
Relative biomass from 2019 - 2025 using M = 0.26 y-1 increased under scenario of 3,000 and 3,500 tons of annual catch quota (Fig. 4A); for a 4,000 tons quota scenario, relative biomass increased less. A catch quota greater than 4,200 ton yielded a biomass depletion of 25 % B1 by 2025. Using M = 0.38 yielded more conservative biomass depletion. Relative biomass increased with annual catch quotas ≤ 4,000 ton.
Production Function
Function # 5 was a “clear winner”, having the lowest AICc and weight Wi greater than 90 % (Table 2). This function was:
Table 2 Parameters and model selection of six Cobb-Douglas production function cases. A in case 6 is catchability q. Bold numbers are predetermined values. The winning model parameters are in bold in the W i .
Tabla 2 Parámetros y selección de modelo entre seis casos de la función de producción Cobb-Douglas. A en el caso 6 es capturabilidad q. Los números en negritas son valores predeterminados. Los parámetros del modelo ganador están en negrita en el W i .
| Case | Parameters | A | µ | ν | AICc | ΔAICc | W i |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 1,099.8 | 0.226 | 0.00000 | 115 | 20.0 | 0.0 |
| 2 | 3 | 1046,675.34 | 1 | 0.00000 | 158 | 63.6 | 0.0 |
| 3 | 3 | 0.49 | 0.073 | 1 | 103 | 7.8 | 2.0 |
| 4 | 3 | 31.21 | 0 | 0.57 | 102 | 7.1 | 2.8 |
| 5 | 3 | 1,099.8 | 0.226 | 0 | 95 | 0.0 | 95.3 |
| 6 | 2 | 0.0019 | 1 | 1 | 113 | 18.3 | 0.0 |
Yield is related to effort but not to stock biomass: μ = 0.226 implies existence of congested fishing effort, indicating that an increase unit effort decreases mean CPUE.
Bionomic Analysis
Price per kilogram of corvina between 2011 and 2019 was MXN 12.5 and remained almost stable during that period, mean price of gas bladder was MXN 279 per kg and fluctuated slightly, and mean price of gonad was MXN 87 per kg and showed a slight increase over time (Licón-González et al., 2023). The average catch per trip of a fishing boat is 1,135 kg and over 90 % of the cost structure belongs to variable costs. Out of a total of MXN 2,895 per kg, 40 % and 35 % correspond, respectively, to gasoline and gutting (EDF, 2016).
Since catch is independent of biomass, fPEC and fEEC do not converge, which reflects lack of bionomic equilibrium (Fig. 5). fEEC constant = 2,379 fishing units, never reached equilibrium because fPEC approaches 557 when biomass approaches zero. In a free access scenario, effort would grow until the corvina is exhausted, before reaching bionomic equilibrium. fMEY is reached with 348 small boats (Fig. 6). A remarkable result is that fPEC at 0.25B1 with only 477 small boats, meaning that increased fishing effort compromises sustainability of the fishery.
Discussion
Despite problems of CPUE known since decades ago (Coppola and Pascoe, 1998; Maunder et al., 2006), surplus production models will likely continue in use because catch-effort are easy to collect (e.g., Urías-Sotomayor et al., 2018; Alam et al., 2021; Angelini et al., 2021; Meissa et al., 2021). We highlighted how assessments can be done with ancillary fishery-independent data. When fish form aggregations that increase catchability and CPUE, use of a Cobb-Douglas production function can overcome problems associated with hyperstability. For our case study, we were able to derive meaningful management information for the gulf corvina. This is important because official annual assessments use Schaefer’s production function (e.g., Ruelas-Peña et al., 2013).
Our approach captured interannual dynamics of corvina. Fluctuations of ca. eight years seem to indicate cyclical events. Within a fishing season, tidal cycles also influence availability of corvina (Román-Rodríguez, 2000); hence mid-term cycles and lunar effects could be linked and influence corvina. The only lunar cycle with a period of 8.85 y is displacement to the east of the lunar perigee; this produces intense spring tides approximately every 4.4 y (Haigh et al., 2011). Such variability should be considered in modelling to inform management of corvina.
Although SRA is a deterministic procedure, using two estimates of M and an interval of 25 % and 75 % of 2013-2015 (see below) allowed to address uncertainty of assessments. B1 estimates in this work might be considered “virgin” biomass (Bv) because initial catch represents a relatively low fishing effort. Thus, estimates of ratio of final to initial biomass means that stock biomass of corvina at the upper gulf of California is between 25 % and 34.5 % of Bv, being both lower than 0.5Bv estimated by Enciso-Enciso (2014).
Lower stock size is associated with M = 0.26 y-1 and higher wit M = 0.38 y-1; thus, a good M estimate is important to assess this fishery. The two M values used in the present study were estimated by Erisman et al. (2014) from empirical formulas of Pauly (1980) and Jensen (1996). Both were the best of 30 formulas for assessments with limited data (Kenchington, 2014). With M = 0.26, solutions to SRA catch equations were restricted to the range of exploitation rates estimated by Erisman et al. (2014) for 2013 - 2015 (from 25 % to 75 %). In contrast, with M = 0.38, no solutions were possible for the entire range of E ̅ 2013-2015 used. Solutions were only found when mean value and lowest of these exploitation rates were used. The only viable solution with M = 0.38 was found using as constraint the lowest estimated exploitation rate during the 2013 - 2015 seasons. Consequently, the value of M for this species is closer to 0.26 than 0.38 y-1. Because of this, true biomass at the end of 2019 may be closer to 0.25Bv than 0.35Bv.
The gulf corvina stock is in worst condition than previously estimated by Enciso-Enciso (2014) who considered to be optimal, close to 0.5Bv. A condition of the gulf corvina between 0.25Bv and 0.35 Bv is of concern since the lowest has been a biomass level where all common functions of stock-recruitment predict depensation or reduced recruitment (Beverton and Holt, 1957; Ricker, 1975; Barrowman and Myers, 2000), which could be defined as limit reference point for management (Caddy and Mahon, 1996).
Our results agree with Mendívil-Mendoza et al. (2018): the fishery is unsustainable because it is based on mega-breeders. In other words, this fishery’s profitability and continuity relies heavily on aggregated fish and therefore cannot be considered as a fishery where random distribution of fish plays a key role. Results of Erisman et al. (2020) coincide with ours. They estimated that yield per recruit was 73 % of maximum possible for this population. Erisman et al. (2014) found contradictory results regarding stock status in 2012. The low abundance of mega-spawners and an analysis of spawning potential indicated overexploitation; but increasing average corvina sizes in catches related to regulations of mesh size indicated sustainability. From 2009 to 2019, however, catch size gradually decreased at a rate of 1 cm y-1 (INAPESCA, 2021).
This fishery has been managed with annual quotas between 4,000 and 4,500 tons between 2015 and 2020; in 2021 this was increased to 5,128 tons. Our projections with SRA show that a < 4,000 tons quota recover the stock. Catches above 4,000 tons are only possible if M = 0.38 y-1 but the stock status remains close to the limit point 0.25Bv.
The best Cobb-Douglas production function indicated that as effort increases fishers compete, reducing their overall catchabilities. The zero-exponent obtained for biomass indicates that catch is independent of abundance; it depends on effort, which supports the hypothesis of hyperstability. For the same reason, fPEC and fEEC do not converge, indicating absence of a bionomic equilibrium, and that under open access fishing effort can deplete the stock.
Spawning aggregations can withstand increased catch rates despite stock reduction until the fishery collapses. Although catch is independent of biomass, a reduction lower than 0.25B1 compromises sustainability of the stock, achieved with a fishing effort of 477 boats. In 2019, 450 boats operated close to the limit. Currently, 737 boats possess fishing permits for gulf corvina; this threatens the fishery because all too often quotas are not enforced (Mendívil-Mendoza et al., 2018). Even if quotas were not exceeded, excess fishing units beyond economic optimum signifies reduced catch rates and, most likely profits, due to effort crowding.
Stimulus to increase catch follows a concomitant increase in market prices. When catches increase early in the fishing season, market saturates and price plummets. Recent interest to market gonads and crops increases income, which increase catches (EDF, 2016).
In 2016, catches concentrated in the first month of the season, saturating the market and lowering the price from $15,000.00 MXN/ton (USD 779.22) to $8,000.00 MXN/ton (USD 415.58); in the following month catches decreased by a third (EDF, 2016). This indicates that the price reduction observed in 2015 can reduce effort due to low profitability.
Our economic analysis assumed constant prices and costs; an elastic price could change these results. Market saturation in the first month causes reduction in price (EDF, 2016). However, in recent years the price of gutted product seems to follow a supply-demand relationship, but price stabilizes complementing with sale of swim bladders and gonads.
Annual quota disregards hyperstability, which can be overcome using nonlinear production functions and fisheries-independent data. With this approach, we found that the gulf corvina biomass is close to 25 % of virgin stock, which calls for precautionary management to avoid economic collapse to the fishery and reduced viability of this species. Quotas need be precautionary strict enforcement is needed.
Conclusions
Disregarding spawning aggregations can prevent accurate assessments that may cause stocks to collapse.
Hyperstability can be included using non-linear production functions such as the Cobb-Douglas. Ancillary information can also be used in data-poor situations.
The gulf corvina (C. othonopterus) forms seasonal spawning aggregations which increase its vulnerability. Currently, assessment and estimation of annual catch quotas are done disregarding hyperstability of the stock. This can be overcome using nonlinear production functions and ancillary, fisheries-independent data.
We found that the gulf corvina biomass is close to 25% of virgin stock, which requires precautionary measures to avoid economic fishery collapse compromising viability of this endemic species.
The gulf corvina fishery continues to occur and yields revenues not because of the randomness of common fisheries, but because of the spawning aggregations it relies upon. Costs of fishing are reduced and, therefore, profits are positively influenced by the gregarious nature of mega spawners in a relatively small space. Therefore, fishers and managers should reduce current fishing mortality and determine a maximum size limit so that mega spawners can continue to contribute to annual recruitment. A maximum size limit in combination with an annual quota need to strictly be enforced so that this endemic species can continue to be the basis of an important social and economic activity.











 nueva página del texto (beta)
nueva página del texto (beta)







