1. Introduction
The conditions for developing countries to achieve high and sustained rates of growth are paramount to economic discipline. The argument that the capacity for economic growth can find its main restriction on demand constitutes one of Anthony Thirlwall's main contributions in this field.
Within the framework of this theory, the possibility that the observed rate of output growth influences the natural rate of economic growth, in which the rate of unemployment remains constant, is a fundamental piece. In neoclassical theory, the natural rate is assumed to be exogenously defined by population growth and labor productivity growth. León-Ledesma and Thirlwall (2002) propose that, in reality, this natural rate is determined endogenously by the economy's actual performance; during a boom, the economy's capacity also increases because more resources are used and greater labor productivity is achieved. The opposite occurs during recessions.
This theory has been tested extensively in different countries and periods, and the available evidence strongly supports it. However, growth has been low in recent decades in Latin America; the economic crises led to abrupt falls in production in 2009 and 2020. Therefore, verifying that this thesis is still valid for Latin America is fundamental. This paper aims to analyze the endogeneity of the natural rate of economic growth for a sample of eleven Latin American countries from 2000-2023. Based on the methodology proposed by Vogel (2009), our contribution is to provide updated evidence of the endogeneity of the natural rate of growth for these countries. The seemingly unrelated regressions (SUR) model results show that León-Ledesma and Thirwall's argument remains valid. Therefore, if the natural rate of growth is endogenous to the real output growth rate, it is essential to consider demand, supply, and balance of payments restrictions to strengthen modern growth theory.
The paper is organized as follows. After this introduction, the theoretical aspects of the natural rate of growth proposed by Thirlwall and based on Harrod's work are described. Later, the results obtained from empirical tests of this hypothesis in European, Asian, and Latin American countries are reviewed. Then, the methodology and data are defined, and the results are presented and discussed. Finally, some reflections derived from the analysis are presented.
2. Theoretical considerations
Within the framework of dynamic economics, Harrod (1939) formulated a taxonomy that allowed him to explain the income rate of growth to guarantee an expanding economy. The observed rate of output growth (g a ) is the ratio between the savings rate and the capital ̶ output ratio. However, g a does not necessarily guarantee equality between savings and investment in the sense of national accounting. The guaranteed growth rate of output (g w ) is determined by "the Relation," an accelerating mechanism in which planned savings and investment are functions of income that balance to maintain full employment of capital.
According to Harrod (1939), the instability of the economic system lies in the movements of g a caused by the gap between the observed growth and the g w . In this sense, it is possible to ensure full employment of productive capacity when both rates are equal, but this does not necessarily ensure full utilization of employment, i.e., of the labor force, which depends on the natural rate of growth (g n ), which in turn is composed of two rates of growth determined exogenously, namely: that of the labor force and that of labor productivity. It is the maximum rate of growth permitted by population growth, capital accumulation, technological improvement, and the preference program between work and leisure, assuming that there is always full employment (Harrod, 1939, p. 30). The divergence between g a and g n increases or decreases structural employment. Therefore, the natural rate of growth must be the rate that keeps the unemployment rate constant. Likewise, g a = g w = g n is required by mere coincidence to achieve full employment.
Harrod's model received much criticism, focusing on construction, its mathematical characteristics, and its application in countries with a lower degree of development trying to undertake a stage of economic improvement with complex initial conditions such as capital scarcity. However, Harrod's ideas also expanded the research programs of thought doctrines. One of the most representative reactions of the dominant theory on the supply side was Solow's growth model (1956), which assumes that g n is determined exogenously. In this way, full employment is achieved by continuously adjusting the capital ̶ output ratio, which will result in the convergence of the guaranteed and natural rates of growth.
On the other hand, Kaldor (1957) developed a model of economic growth in which there is an interdependent relationship between capital accumulation and technological progress. In that case, the stylized facts are the basis for the capital-product ratio to remain unchanged (due to some externality or diminishing returns) but not the capital-labor ratio. The outline of his version of the rate of natural growth lies in the impact of capital accumulation on the rate of growth of labor productivity in the short run. However, in the long term, g n is exogenous due to the role of technological progress.
Kaldor (1966) used Verdoorn's Law (1949) to explain a positive causal relationship between the growth of manufacturing labor productivity that depends on the increase of the output of the same sector. The transmission mechanism indicates that when industrial production and employment expand, the labor force is absorbed from those sectors with open unemployment or underemployment. This transfer of workers does not decrease the production of any sector but increases productivity outside the industry. Likewise, static and dynamic increasing returns within the manufacturing sector have to do with the size and scale of the productive units and the induced technical progress, respectively. Harrod's model was the starting point for different theoretical and empirical exegeses that contributed to the advancement of the economic discipline. Over more than four decades, economists incorporated - from diverse theoretical perspectives - new elements to explain the nature of economic growth of countries and also between nations or regions, which gave rise to a "new" theory of endogenous growth (Lucas, 1988; Barro, 1991; Barro and Sala-i-Martin, 2005). However, a common denominator of these predominantly supply-side studies is that the rate of growth was considered exogenously.
From a perspective where demand determines or restricts economic growth, León- Ledesma and Thirlwall (2002) and Thirlwall (2003) reject the idea that g n is exogenous. If it is now considered that the growth rates of the labor force and productivity are positively related to g a , the speed of adjustment between g w and g n in Harrod’s model would be different, which would explain the difference in economic growth between countries. Ergo, g n should be considered endogenous.
León- Ledesma and Thirlwall (2002) and Thirlwall (1969; 2003) use a modification of Okun's law (1962)1 to estimate the endogeneity of the natural rate. In Harrod's model, the unemployment rate depends on the divergence between g a and g n ; that is, constant unemployment is subject to the behavior of this gap. If we link the ideas of Harrod (1939) and Okun (1962), then:
Where % U is the percentage unemployment rate, and g is the rate of growth. When ∆ % U = 0, g is defined as g n =a/b . According to the authors, the coefficient b estimate may be biased downwards due to workers' resistance to leaving the labor market during periods of recession, which could lead to an overestimation of g n . At the same time, the term a could underestimate the dependent variable as a consequence of leaving the labor market. Therefore, it is difficult to know a priori what the net balance of these two forces will be. These biases can be avoided by estimating:
This equation defines g n by the constant a 1 when ∆ % U = 0. According to Ledesma and Thirlwall (2002) and Thirlwall (2003), there is also the possibility of statistical problems in the estimation of equation (2) because the variation in unemployment is not exogenous. Still, the extent of the possible bias cannot be determined in advance. However, it is possible to test for endogeneity by including a dummy variable in equation (2) during periods where the observed rate of growth is greater than the estimated natural rate and then testing its significance. That is to say:
D is a dichotomous variable that takes the value of one when g a > g n and zero in other cases. If the coefficients a 2 and b 2 are significant and the sum of both is larger than a 1 , then the natural rate of growth must have increased compared to the rate of growth observed in boom periods. That is to say, more workers were incorporated into the labor market, increasing productivity. In this case, the natural rate of growth must be endogenous to the actual rate of growth.
In this context, different empirical studies analyze the differences in the economic rate of growth between countries or regions considering the endogeneity of the natural rate. These are described below.
3. A brief survey of the empirical literature
The hypothesis of endogeneity of the natural rate of growth presented in the previous section has been tested empirically for a diverse set of countries. Most of the studies follow the two-stage methodology proposed by Thirlwall (1969). First, the natural rate of growth is estimated based on the relationship between growth and unemployment, as suggested by Okun (1962); the natural rate of growth is defined as the rate of growth that keeps the unemployment rate constant. The natural rate of growth is obtained by estimating Okun's Law, directly or indirectly; the latter is known as Thirlwall's reversal. Subsequently, the endogeneity of the natural rate is tested by incorporating a dummy variable that identifies boom periods in which the observed rate is greater than the natural rate. If the coefficient of this variable is significant, it confirms that the natural rate responds to changes in the observed rate and, therefore, it is not determined exogenously.
In their pioneering work, León-Ledesma and Thirlwall (2002) tested the endogeneity of the natural rate of growth for a sample of 15 OECD countries in the period 1961-1995, containing countries in different economic contexts.2 The natural rate of growth is estimated by applying Ordinary Least Squares (OLS) to the methodological proposal of Thirlwall (1969) in both specifications; as occurs in most subsequent studies, Thirlwall's reversal specification yields more robust results. Significant results are found for all countries in the sample; the natural rate of growth varies between 4.57% for Japan and 2.54% for the United Kingdom. Also, there is a significant difference between the natural rate of growth and the observed rate of growth of 1.42 percentage points on average, which implies an average elasticity of 40.1%. Therefore, clear evidence supports the endogeneity of the natural rate of growth.
Dray and Thirlwall (2011) test the endogeneity hypothesis for 10 Asian countries from 1982-2005.3 Regarding the natural rate of growth, they found significant results for 8 out of the 10 countries (no evidence was found for Japan and the Philippines on the relationship between growth and the change in the unemployment rate). The natural rate of growth varies between 10.36% in China and 2.8% in the Philippines. Likewise, the results are statistically significant in the endogeneity of the natural rate of growth, except for the Philippines. The increase in the natural rate of growth in boom periods varies between 1.74 percentage points in South Korea and 4.56 percentage points in Hong Kong; with an average of 30.1%, elasticities vary from 10.7% in South Korea to 66.24% in Japan. These elasticities are lower than those found for the OECD countries.
Perrotini and Landa (2015) analyze the elasticity of output to demand for a group of 18 Eurosystem countries for the period 1980-2012. The estimation uses fixed effects panel models for both the panel and individual countries. The average natural rate for normal phases of the economic cycle is 2.8%; the rate varies between 1.8% for Belgium and 5.1% for Luxembourg. Evidence is found of the procyclical behavior of the natural rate of growth and, therefore, of the endogeneity of the natural rate of growth. When the observed rate is greater than the natural rate, it increases by around 1.6%, equivalent to an elasticity of 58.2%; the range varies between 2.7% in France and 7.2% in Luxembourg.
Studies have also been carried out for some countries individually, considering their internal heterogeneity. Lanzafame (2010) analyzes 20 Italian regions for the period 1977-2003. Using the fixed effects estimator of Least Square Dummy Variables (LSDV), as well as Seemingly Unrelated Regression (SUR) techniques, it is found that the natural rate of regional growth is close to 4%. However, the estimators are only significant for 7 of the 20 regions considered. This result should be taken into consideration in the following findings. The author finds evidence in favor of endogeneity; the natural rate of growth increases between 3 and 3.7 percentage points in periods when the observed rate is higher than the natural rate. However, implementing a purely data-driven approach (to investigate the impact of potential cross-sectional heterogeneity) finds partial evidence in favor of the endogeneity hypothesis (in two out of the 20 regions analyzed, a higher natural rate is found when growth is slow). Other studies that have found evidence in favor of this hypothesis are Acikgoz and Mert (2010) for Turkey in 1980-2008 and Carrión and Ochoa (2018) for Ecuador in 1970-2014.
This hypothesis has also been tested extensively in Latin America. For a sample of 11 Latin American countries, Vogel (2009) estimates the natural rate of growth for the period 1986-2003 using Seemingly Unrelated Regressions (SUR). The estimated average natural rate of growth varies considerably; most countries are between 2.64% and 3.03%, but the range varies between 1.78% and 6.12% per year for Venezuela and Chile, respectively. For Mexico, the rate is 2.64%. The results support the endogeneity of the natural rate of growth. On average, the natural rate of growth increases by 2.25 percentage points in boom periods, that is, 64.1% more. For Mexico, this difference is 2.02 percentage points, an increase of 76.52%. Given that these figures are much higher than León-Ledesma and Thirlwall (2002) reported for OECD countries, the greater sensitivity of the potential product to demand for the developing countries studied is emphasized.
Libânio (2009) analyzes a sample of 12 Latin American countries in a similar spirit. The estimated panel data model for the natural rate of growth is significant overall, except for Ecuador; individually, Argentina is the only exception. The natural rate of growth varies between 1.81% for Uruguay and 4.42% for Chile. The procyclical behavior of the natural rate of growth provides evidence in favor of endogeneity. Furthermore, the natural rate behaves asymmetrically during the economic cycle. During periods of growth, the increase in the natural rate ranges from 30% to 188% in the entire sample; on average, the natural rate is double the natural rate throughout the period. Conversely, the natural rate is lower in periods of recession; the average drop in the natural rate in the entire sample reaches 125%. Therefore, aggregate demand influences economic growth in the long term.
Perrotini and Tlatelpa (2003) test the hypothesis of the endogeneity of the natural rate to fluctuations in aggregate demand for Mexico, Canada, and the United States for the period 1970-2000. The elasticity for Mexico is 75%, considerably higher than the figure for the United States (31%) and Canada (17%). Molerés and Perrotini (2013) also found evidence of the presence of endogeneity in these countries from 1971 to 2011 (according to the data available for each country). Using Rolling Regressions techniques, evidence of endogeneity is found; by comparing the natural rate for normal periods and boom periods, there is an absolute difference of 1.84 in Mexico, 1.22 in Canada, and 0.67 in the United States. The elasticity of the natural rate in Mexico is 55.48%, 41.42% in Canada, and 21.6% in the United States. According to the authors, this suggests that the observed rate of growth in periods of expansion induces growth in the labor force and labor productivity, as theoretically expected.
In summary, the studies reviewed provide empirical evidence of the endogenous behavior of the natural rate of growth concerning observed growth for a broad set of developed and developing countries extending over different periods. The mechanisms of this behavior continue to be investigated, both due to labor's response through supply and labor productivity or due to capital-related conditions. Another analytical layer is added according to the possible differentiated effect of these factors due to the economic structure and performance at a given time. For example, Perrotini and Vázquez (2017) propose two types of endogeneity of the natural rate, the first for the product rate of growth, as previously analyzed, and the second for capital accumulation measured through the installed capacity. Vázquez Muñoz and Contreras (2019) applied this model for Mexico at the general and state levels.
4. Methodology
To test our hypothesis, we empirically analyze the endogeneity of the natural rate of growth for a sample of eleven Latin American countries: Argentina, Bolivia, Brazil, Chile, Costa Rica, Colombia, Mexico, Nicaragua, Paraguay, Peru, and Venezuela from 2000 to 2023. Likewise, it is essential to clarify that due to the sample's representativeness and heterogeneity - different degrees of economic development - the choice of countries was based on a previous study by Vogel (2009) from 1986 to 2003. The data used in this work are the historical series of the unemployment rate and real GDP growth, in annual percentage variation, from the International Monetary Fund (see Figures 1 and 2).4
According to Figure 1, the observed economic growth is relatively similar among the eleven countries in the sample. However, it is possible to appreciate the instability of the Venezuelan economy, which since 2014 has maintained increasingly deep rates of decline. Something similar happens in Argentina and Paraguay, whose behavior is not homogeneous with the rest of the nations considered. It is also recognized that the COVID-19 pandemic was more devastating than the Great Recession of 2008.
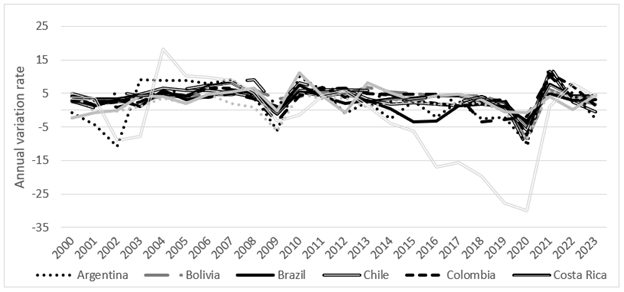
Source: own elaboration with data from the IMF.
Figure 1 Economic growth in eleven countries of Latin America, 2000-2023.
In terms of unemployment, Figure 2 shows the evolution of the unemployment rate for the eleven selected countries. Without a doubt, the economic decline experienced by Venezuela has resulted in unemployment rates greater than 40%. After the economic crisis caused by the COVID-19 pandemic, the increase in unemployment was generalized to other countries, mainly for the Costa Rican economy. However, these nations have been able to recover their level of occupation.
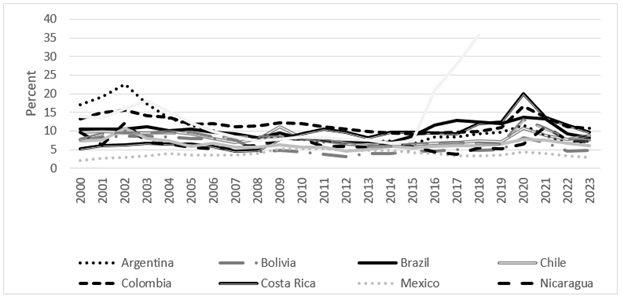
Source: own elaboration with data from the IMF.
Figure 2 Unemployment rate in eleven countries of Latin America, 2000-2023.
First, we use equation (2) to evaluate the natural rate of growth of the Latin American countries considered in the sample. The equations for the first eleven countries, excluding Venezuela, were estimated through the seemingly unrelated regressions (SUR) estimator proposed by Zellner (1962). However, they were carried out separately for Venezuela due to the low availability of data. Table 1 shows the results.
Table 1 Estimation of the natural rate of growth (2000-2023)
| Country | a 1 | b 1 | Natural rate of growth | R 2 | ||
|---|---|---|---|---|---|---|
| Argentina | 1.0675 | * | -0.3376 | *** | 1.07 | 0.7584 |
| Bolivia | 3.6466 | *** | -0.0953 | *** | 3.65 | 0.4865 |
| Brazil | 2.2308 | *** | -0.1580 | *** | 2.23 | 0.5782 |
| Chile | 3.5034 | *** | -0.1096 | *** | 3.50 | 0.5680 |
| Colombia | 3.6880 | *** | -0.1724 | *** | 3.69 | 0.7411 |
| Costa Rica | 4.2262 | *** | -0.0736 | *** | 4.23 | 0.6457 |
| Mexico | 1.8376 | *** | -0.1447 | *** | 1.84 | 0.5183 |
| Nicaragua | 3.3195 | *** | -0.0223 | 3.32 | 0.0394 | |
| Paraguay | 3.3562 | *** | -0.0104 | 3.36 | 0.0174 | |
| Peru | 4.5011 | *** | -0.1228 | *** | 4.50 | 0.5932 |
| Venezuela | 0.6551 | -0.1489 | *** | 0.65 | 0.4315 | |
Note: ***, **, * Denotes significance at the 1%, 5%, and 10% levels, respectively. Due to a smaller amount of data for Venezuela, it was estimated separately.
As we can see in Table 1, the coefficient that measures the response of the observed rate of growth to a change in the percentage variation of the unemployment rate, b 1 , is not significant for Nicaragua and Paraguay. Likewise, for these two countries, the coefficient of determination R 2 was lower than that obtained for the rest of the sample. In the case of Venezuela, the intercept is not statistically significant and is interpreted as the natural rate of growth given the specification of equation (2). On average, the natural rate of growth is 2.91%; it ranges from 1.07% in Argentina to 4.5% in Peru.
In order to test the endogeneity of the natural rate of growth, we estimate a second system of equations by adding a dummy variable to equation (2), as proposed by equation (3), which takes the value of one for boom periods where the natural rate of growth (a 1 ) is above the actual rate of growth (g a ) and zero in other cases. This procedure allows us to determine if the actual rate of growth influences the natural rate of growth during boom periods in the economies of the countries analyzed (see Table 2).
Table 2 Results of the endogeneity test of the natural rate of growth (2000-2023)
| Country | a 2 | b 2 | c 2 | The natural rate of growth | R 2 | |||
|---|---|---|---|---|---|---|---|---|
| Argentina | -1.7305 | * | 5.6646 | *** | -0.1747 | *** | 3.93 | 0.8214 |
| Bolivia | 2.0414 | *** | 2.4568 | *** | -0.0707 | *** | 4.50 | 0.6603 |
| Brazil | 0.9069 | ** | 2.5527 | *** | -0.0995 | *** | 3.46 | 0.7602 |
| Chile | 1.8259 | *** | 3.4674 | *** | -0.0864 | *** | 5.29 | 0.7890 |
| Colombia | 2.7263 | *** | 1.8492 | *** | -0.1392 | *** | 4.58 | 0.7928 |
| Costa Rica | 3.1628 | *** | 1.2295 | *** | -0.0684 | *** | 4.39 | 0.7304 |
| Mexico | 0.8747 | 1.4807 | ** | -0.1149 | *** | 1.48 | 0.5935 | |
| Nicaragua | 0.0722 | 4.8654 | *** | 0.0023 | *** | 4.87 | 0.6016 | |
| Paraguay | 0.5974 | 4.8858 | *** | -0.0175 | *** | 4.89 | 0.6640 | |
| Peru | 2.9439 | *** | 3.2318 | *** | -0.1158 | *** | 6.18 | 0.8150 |
| Venezuela | -6.9186 | *** | 13.5580 | *** | -0.0744 | ** | 6.64 | 0.7778 |
Note: ***, **, * Denotes significance at the 1%, 5%, and 10% levels, respectively. Due to a smaller amount of data for Venezuela, it was estimated separately.
The results in Table 2 show that most of the estimated coefficients of the constant a 2 and slope c 2 are significant at the 99% confidence level, confirming the whole model's significance. It is possible to interpret the continual a 2 as the natural rate of growth in periods of recession, which was not statistically significant for Mexico, Nicaragua, and Paraguay, and it was even negative for Argentina and Venezuela. Our results are similar to what Vogel (2009) found for 1986-2003. Regarding the estimated slope values c 2 , all cases are statistically significant and negative (following what was expected), except for Nicaragua, where it was positive.
The g n in boom periods is obtained from the sum of the coefficients of the constant and the dummy variable (a 2 + b 2 ) as long as both parameters are significant. In cases where the intercept is not statistically significant, the natural rate of growth is equal to b 2 . The fifth column of Table 2 shows that the natural rate of growth estimated using equation (3) is considerably higher than the natural rate of growth for all countries in the sample estimated using equation (2), which provides empirical evidence on the endogeneity of the natural rate of growth concerning the observed rate of growth. Analogous to equation (2) results, the natural rate estimates in boom periods again show a superior range. The average natural rate of growth increases to 4.7%, varying from 2.36% in Mexico to 6.64% in Venezuela. Table 3 summarizes the results obtained through equations (2) and (3), reporting the difference between the average and natural rates in respective boom periods.
Table 3 Sensitivity of the natural rate of growth to the current rate of growth
| The natural rate of growth in boom periods | ||||
|---|---|---|---|---|
| Country | The natural rate of growth | Equation (3) | Absolute Difference | Increase Percentage |
| (equation (2)) | (3)-(2) | (3)-(2) | ||
| Argentina | 1.07 | 3.93 | 2.86 | 267.67 |
| Bolivia | 3.65 | 4.50 | 0.85 | 23.24 |
| Brazil | 2.23 | 3.46 | 1.23 | 55.14 |
| Chile | 3.5 | 5.29 | 1.79 | 51.24 |
| Colombia | 3.69 | 4.58 | 0.89 | 24.00 |
| Costa Rica | 4.23 | 4.39 | 0.16 | 3.84 |
| Mexico | 1.84 | 2.36 | 0.52 | 28.01 |
| Nicaragua | 3.32 | 4.94 | 1.62 | 48.72 |
| Paraguay | 3.36 | 5.48 | 2.12 | 63.19 |
| Peru | 4.5 | 6.18 | 1.68 | 37.24 |
| Venezuela | 0.65 | 6.64 | 5.99 | 921.45 |
| Average | 2.91 | 4.70 | 1.79 | 138.52 |
On average, the natural rate of growth in the sample increases by 1.79 percentage points in boom periods, representing an increase of 61.51%, a value very similar to that reported by Vogel (2009) for the same countries in the period, which goes from 1986 to 2003. However, six of the eleven countries report a moderate increase, less than 50%, while the other five show an extremely high sensitivity of the natural growth rate vis-à-vis the actual growth rate of output, with increases in boom periods ranging from 51.24 to 921.45%,
5. Some final reflections
For decades, supply-side economic growth models have considered the natural rate as exogenously determined. However, based on the ideas of Harrod (1939) and from a vision of demand, León Ledesma and Thirlwall (2002) proposed the endogeneity of this rate concerning the real or actual one. Empirical studies have verified this hypothesis for different economies around the world. Likewise, some analyses incorporate the role of capital accumulation.
This research is inspired by the methodology of Vogel (2009), who emphasizes the importance of sustaining high levels of internal and external demand for goods and services. The endogeneity of the natural rate of growth implies that an automatic convergence of the actual rate of growth to the steady-state equilibrium cannot be expected. Consequently, cumulative growth processes begin through more extensive demand growth in boom periods, which endogenously improves employment and productivity growth. However, several conditions would have to be met to ensure a sustained high level of demand in Latin American countries. First, the enormous gap in income distribution between the poor and the rich has to be substantially reduced to create greater demand for domestic goods. Secondly, it is necessary to establish a higher level of education and political stability to facilitate the creation of an industrial sector that promotes the production of higher value added export goods.
According to the results of our estimation of eleven Latin American countries, the hypothesis of the endogeneity of the natural rate of growth is met for the majority of the countries in the sample. Economic policy implies that in these countries with different degrees of development, it is possible to achieve higher economic growth in the long term, considering this endogeneity relationship. Although this research is robust, several aspects exist to be yet analyzed, such as specific supply, demand, and balance of payments restrictions.











 nueva página del texto (beta)
nueva página del texto (beta)


