Electrolyte Medium

The aggressive solutions were 1 M HCl prepared by dilution of 37 % w/w HCl (Merck) using double distilled water. All tests were performed in aerated medium at different temperatures 20 °C, 30 °C, 40 °C, 50 °C and 60 °C.

Plant extracts

Ephedra major is a plant whose species are widespread in countries and regions of the world characterized by temperate climates. Passing through North Africa, southwest and central Asia, China and southern Europe to North America, most ephedra species grow in coastal regions and in sandy soils exposed to direct sunlight. In this study, the plant was collected in the region of Bejaia located on the Algerian coast. Ephedra major leaves and stems extracts were collected, shade dried, this dry matter was cut into small parts and immersed in a hydroalcoholic solution (methanol/water, 7/3, V/V) for 24 h. Once the mixture has been filtered, the filtrate is immediately evaporated to dryness. Then boiled water is added to the acquired residue, everything is stored at room temperature. After overnight, the mixture is filtered by the use of ordinary filter paper and subjected to liquid-liquid extraction using several solvents separated in sequence of increasing polarity starting with methylene dichloride, ethyl acetate and n-butanol. At the end, the organic phase was collected for each solvent and the solutions obtained were evaporated to dryness by a rotary evaporator (Model RE52A, China, max capacity 2 L, speed range 0-150 rpm) in order to obtain the extracts of the plant.

Weight loss measurements

Gravimetric experiments were conducted in a glass vessel. 32CrMoV5 mild steel of with a composition (wt %): C 0.33 %, Cr 1.25 %, Mo 1.2%, Mn 0.9 %, Ni 0.75 %, V 0.3 %, Al 0,2 % and Fe balance, was used in this investigation. Specimens of dimension 1×1×1 cm were prepared and abraded successively with different grades of emery papers, washed with distilled water, cleaned with acetone, and dried at room temperature. After being weighed accurately with high sensitivity balance, the specimens were immersed in 100 mL 1 M HCl with and without various concentrations of the extract (200,400, 600 and 800 ppm) at different temperatures (20-60 °C) in aerated condition. After 5 h, three test pieces were taken out of the test solution, washed, dried, and weighed again. To confirm the reproducibility of the results, all tests were repeated three times.

Electrochemical measurements

The electrochemical measurements were conducted on a Voltalab-PGZ 301 potentiostat controlled by a computer using Voltamaster 4 software. All the electrochemical setups were carried out in a three-electrode cell, open to the atmosphere. The mild steel as the working electrode (WE), saturated calomel electrode: Hg/Hg₂Cl₂/KCl_sat (SCE) as reference electrode (RE) and platinum electrode as counter electrode (CE). The working electrode was protected by the epoxy resin leaving a working surface equal to 0.5 cm².

Potentiodynamic polarization

The extrapolation of cathodic and anodic Tafel lines was carried out in a potential range starting from a cathodic potential of − 250 mV to an anodic potential of + 250 mV relative to the OCP at scan rate of 0.5 mV s^-1. To obtain the corrosion current densities (I_corr), the linear segments of Tafel anodic and cathodic curves were extrapolated to the corrosion potential. Before starting the experiments, the working electrode was immersed in the test solution for 60 min to reach a state of stability. Electrochemical measurements were performed after open circuit potential (OCP) was measured.

Electrochemical impedance spectroscopy

Measurements by EIS are carried out at the OCP, over a frequency range from 100 kHz to 10 mHz with a perturbation using a signal of equal amplitude at 10 mV. As same as weight loss measurements, experiments were repeated at least three times to check the repeatability.

SEM analysis

The specimens for surface morphological examinations were immersed in 1 M HCl solution containing the optimum concentration of inhibitor (800 ppm) and test solution for 5 h at 20 °C. Then, they were removed, washed quickly with distilled water, and dried. The analyses were observed using SEM (JEOL JSM-6360 LV).

Fourier transform infrared spectroscopy

The FT-IR was used to identify the functional group present in EBEM extract.

Phytochemical screening

Phytochemical analysis shows that Ephedra major plant extract contains saponins, tannins, flavonoids, alkaloids, heterosids and coumarins. The result of phytochemical analysis of Ephedra major plant extract is shown in Table 1 ^[20].

Characterization of the prepared extract

The FT-IR spectrum of the butanolic extract of Ephedra major is shown in Fig.1. The spectrum shows absorption peaks of 3552 and 3342 cm^-1, which are assigned to the stretching vibrations of N-H. The wavenumbers around 1600-1200 cm^-1 are due to stretching C=C, C=O, OH and C=N, while around 800-500 cm^-1 they are attributed to the presence of C-C, C-O, =C-H and C-N. This shows that EBEM plant extract contains mixtures of compounds, i.e. amides, amines, aromatic and organic acids.

Fig. 1 FT-IR spectrum butanolic extract of Ephedra major. 

Weight loss measurements

The corrosion parameters obtained by conducting weight loss measurements for mild steel in the absence and presence of different concentration of Butanolic extract of Ephedra major (EBEM) in 1 M HCl solution after 5 h of immersion at different temperatures in the 20-60 °C range, were calculated are given in Table 2. The corrosion rate (CR) was calculated, in milligrams per square centimeter per hour (mg cm^-2 h^-1), from the following equation ^[21]:

Where, ∆W is the average weight loss (mg), S is the total surface area of the specimen (cm²) and t is the immersion time (h). The inhibition efficiency can be calculated using the equation reported in the literature ^[21]:

Where, CR0 and CRi are the corrosion rates in the absence and presence of various concentrations of inhibitor respectively. The corrosion rate (CR), the surface coverage (θ) and the inhibition efficiency (IE_w %) is very useful to discuss the adsorption characteristics and thermodynamic parameters were calculated.

Fig.2 shows the evolution of inhibitory efficiency and corrosion rate of 32CrMoV5 steel immersed in 1M HCl for 5 hours at 20 °C as a function of the EBEM concentration. The curves show that the corrosion rate decreases and reaches a value of 0.0539 mg.cm^-2.h^-1 at 800 ppm while the inhibitory efficiency increases with increasing inhibitor concentration. Table 2 shows the values obtained for the corrosion rate CR (mg.cm^-2.h^-1), the inhibition efficiency values IE_w (%) and surface coverage (θ) at 20 °C.

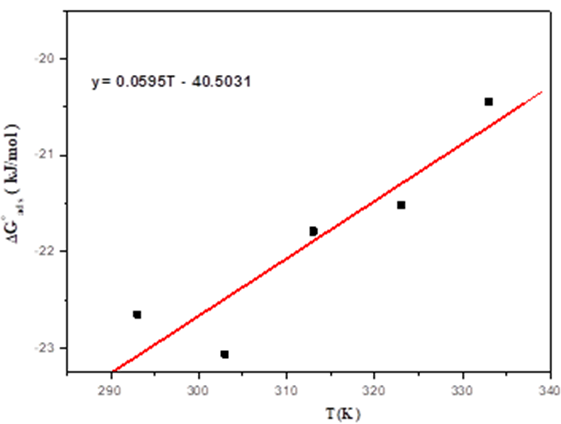
Fig. 2 Evolution of the corrosion rate and the inhibitory efficiency as a function of different concentrations of EBEM calculated from the weight loss method at 20 °C 

According to Table 2, the following observations can be drawn:

The inhibitory efficiency and the surface coverage increase while the corrosion rate CR decreases with increasing EBEM concentration.

The inhibitory effect of EBEM increases with increasing inhibitor concentration and reaches the maximum value of 84.81 % in the presence of 800 ppm. This behavior can be explained by a large adsorption of the n-butanol extract of the plant Ephedra major on the surface of the metal and covers the active sites of the surface, which causes the formation of a barrier layer, which reduces the reactivity of the metal on the surface of mild steel 32CrMoV5.

An increase of inhibitor concentration beyond 800 ppm resulted in a diminished corrosion protection. This may be due to the withdrawal of adsorbate (EBEM) back into the bulk solution when the concentration of inhibitor closed to or beyond the critical concentration ^[22,^23]. The above effect leads to the weakening of metal-inhibitor interactions, resulting in the replacement of inhibitor by water or chloride ions (Cl⁻) with a decrease in inhibition efficiency ^[23,^24].

The extract has good inhibiting properties against corrosion of steel in 1 M HCl medium. Fig.3 shows the evolution of inhibitory efficiency for different extract concentrations in 1M HCl solution over the temperature range of 20-60 °C. The change of the corrosion rate with the temperature was studied in 1M HCl, both in the absence and presence of EBEM. It is observed that the rise in temperature accelerated the corrosion reaction, resulting in an increased corrosion rate. Generally, in acidic media, dissolution of metal is accompanied by evolution of hydrogen gas and a rise in temperature usually accelerates the corrosion reactions, resulting in higher dissolution of metal. However, the inhibition efficiency increases with increasing EBEM concentration, which can be attributed to some chemical changes occurring that phytochemical component of the extracts are absorbed onto the mild steel surface, resulting in blockage of reaction sites and protection of the mildsteel surface from attack by corrosion-active ions in the acid medium ^[25,^26].

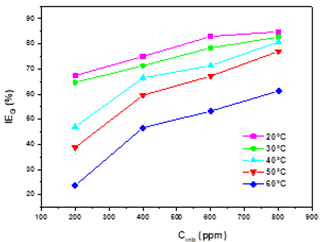
Fig. 3 Evolution of the inhibitory efficiency as a function of different concentrations of EBEM calculated from the weight loss method at different temperature 

The further rise in temperature, decreased the inhibition efficiency showing a phenomenon of the quick desorption of adsorbed inhibitor molecules from the surface (Table 2), the protective layer formed on the surface of the steel by adsorption of the plant extract is destroyed and is no longer resistant. Generally, the effect of temperature on the inhibited acid-metal reaction is very complex, because many changes occur on the metal surface such as rapid etching and desorption of inhibitor and the inhibitor itself may undergo decomposition ^[27,^28]. According to Ammar et al. ^[29], this phenomenon was explained by the high sensitivity of the Van Der Waals-type physical interactions between the iron surface and the inhibitor. Table 3 shows the obtained values of percentage inhibition (IE_W), corrosion rate (CR) and surface coverage (θ) are summarized in Table 2 at different temperatures.

Potentiodynamic polarization

In order to know the kinetics of anodic and cathodic reactions, potentiodynamic polarization measurements were carried out to gain insight into the kind of corrosion protection supplied by EBEM. Experiments were performed in the absence and presence of different concentration of EBEM. Experiments were performed in the absence and presence of different concentration of EBEM. Fig.4 displays polarization plots of mild steel 32CrMoV5 immersed in 1M HCl at 20 °C, in the absence and presence of different concentrations of EBME. Electrochemical parameters such as corrosion potential (E_corr, mV/SCE), cathodic and anodic Tafel slopes (β_c, β_a, mV/dec), the corrosion current density (i_corr, mA.cm^-2) and inhibition efficiency (IE_p%) are given in Table 3. The (IE_p %) is calculated according to the Equation bellow:

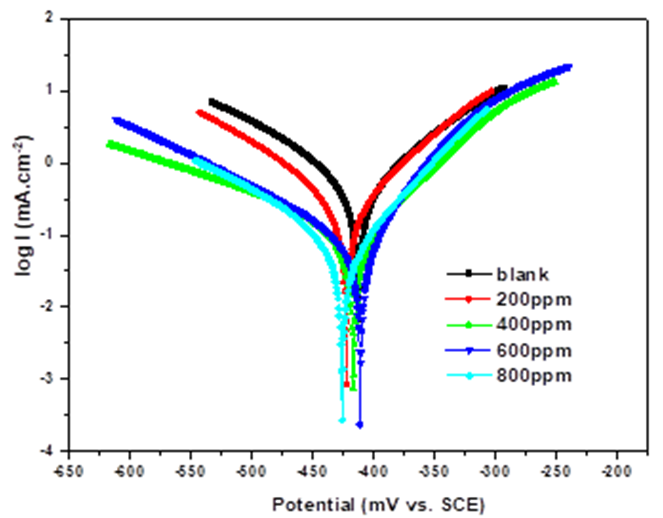
Fig. 4 Tafel curves of mild steel obtained at 20 °C in 1 M HCl solution containing different concentrations of EBEM. 

Where icorr0 and icorrinh are the corrosion current densities in the absence and presence of the inhibitor (EBEM extract), respectively.

As reported by in Table 4, the following points can be raised:

E_corr was approximately constant ; the change in value of E_corr with respect to the corrosion potential of the blank is lower than 85 mV reflect the mixed type of inhibition ^[30,^31].

The addition of extract EBEM decreases the current densities anodic and cathodic current.

The parallel cathodic Tafel lines suggest that the addition of EBEM shows that the proton

reduction reaction on the surface of the steel is not modified, this indicates that the mechanism of hydrogen evolution mainly due to charge transfer ^[31,^32]. This behavior was ascribed to adsorption of the extract molecules covering the active centers present ᴏn the steel surface ^[20,^33].

The inhibition efficiency increases with increase in concentration for EBEM, while the corrosion current densities decreased. These results signify that the extract was good inhibitor for mild steel in acidic solution.

Electrochemical impedance spectroscopy (EIS)

EIS measurements were performed to study the impedance parameters to provide a deeper insight regarding the corrosion protection in 1 M HCl at various concentrations of EBEM at 20 °C. The working electrode was soaked in the test solution for 45 min before each experiment in order to achieve a quasi-stable condition. Nyquist and Bode plots of mild steel in uninhibited and inhibited acidic solutions containing various concentrations of Butanolic extracts of Ephedra major are shown in Fig.5.

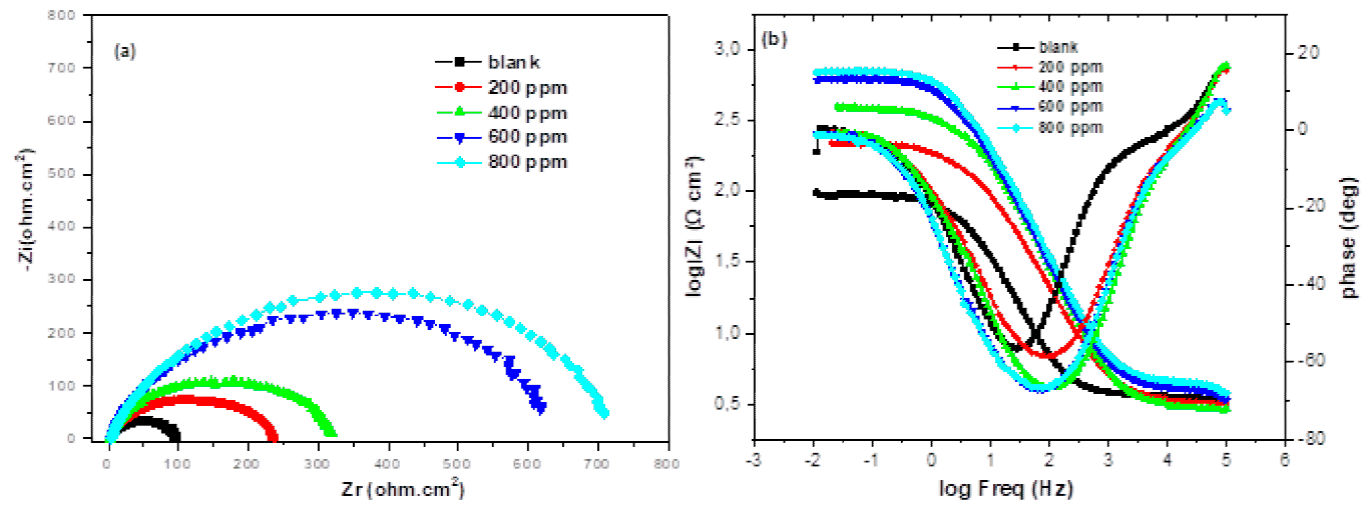
Fig. 5 Nyquist (a), Bode and phase angle (b) plots for mild steel in 1.0 M HCl with and without different concentrations of EBEM at 20 °C. 

As shown in Fig.5 (a), it can be observed that the impedance spectra data has significantly changed with the addition of the extract, but these diagrams have similar shape for all tested concentrations, indicating that there is almost no change in the corrosion mechanism whether the inhibitor is added or not ^[31,^34]. From these plots, the impedance containing a depressed semicircle, whose diameter increases with increasing extract concentration, indicating a charge transfer process, mainly controlling the corrosion of mild steel ^[4,³⁵,^36]. In addition, these diagrams (Nyquist) contain a semicircle which is not a perfect, which is often referred to as frequency dispersion as a result of the inhomogeneity ^[23, ^37] or the roughness, impurities and dislocations ^[38] of the solid surface. This finding is confirmed by the depiction of Bode diagrams where the existence of an equivalent circuit containing a single constant phase element in the steel/acid interface is observed. In addition, at low frequencies in the Bode diagram, the increase in absolute impedance confirms the the higher protection with the increase in the concentration of the inhibitor, which can be explained by the adsorption of the EBEM compound on the surface of the mild steel ^[39]. From Fig 5(b), the phase angle plots increase with the decrease of EBEM concentration, this increase is due to the formation of a protective film on the mild steel surface. While the increase in the |Z| modulus (Fig. 5(b)) indicates the good performance of the inhibitor with a constant time period for different concentrations of EBEM ^[40]. According to these results, adsorption takes place on the surface of mild steel leading to the formation of a protective thin film that inhibits the dissolution of mild steel in HCl medium. The phase angle values for the EBEM used were still higher than the blank but lower than -90 °, indicating a non-ideal capacitor. The inhibition efficiency was calculated from Nyquist plots, according to the following Equation:

Where, R'p and Rp represent the polarization resistances in the presence and absence of inhibitor, respectively. Inspection of data in Table 5 clearly shows the inhibition efficiency (IE_EIS) increase with the increase in concentration at 20 °C and polarization resistances (R_p, Ω.cm²) increases, the double-layer capacitance (C_dl, μF cm−2) decreases (R_p and C_dl have an opposite trend in the whole concentration range). The decrease in this capacity (i.e. thickness growth of the electrical double layer) with an increase in plant extract concentrations may be attributed to the formation of a protective layer on the electrode surface ^[38]. This phenomenon can be explained by the electronegative charge of the heteroatoms contained in the extracts and the electropositive charge on the steel surface ^[41]. For a more in-depth analysis of the corrosion inhibition process, EIS plots have to be fitted with equivalent circuits. The most suitable equivalent electrical circuit (EEC) obtained by fitting the experimental data is shown in Fig.6. It comprises the solution resistance Rs and the polarization resistance R_p, which is the sum of all other resistances (R_p=R_ct+R_d+R_f+R_a) ^[40, ⁴². ^43], where R_ct is the charge transfer resistance, R_d is the resistance of the diffuse layer, R_a is the resistance of the species accumulated at the metal/solution interface, and R_f is the resistance of the inhibitor film on the steel, which is considered only in the presence of inhibitors. The polarization resistance, in parallel (R_p//CPE) with the constant phase element (CPE) which replaces the capacitance of the electrical double layer (C_dl) ^[21, ³⁸, ^39].

Fig. 6 Simple equivalent circuit (EEC) used to fit the impedance data. 

The values of C_dl can be calculated from (CPE) parameter and R_p according to the following Equation ^[21]:

Where n is the deviation parameter of the CPE: 0 ≤ n ≤ 1. The electrochemical parameters including R_p, Q, and n, obtained from the fit and the calculated double-layer capacitance values are listed in Table 5. Simulations of Nyquist and Bode plots led to the equivalent circuit that fitted the experimental data established in 1.0 M HCl medium with and without the presence of the EBEM as shown in Fig.7.

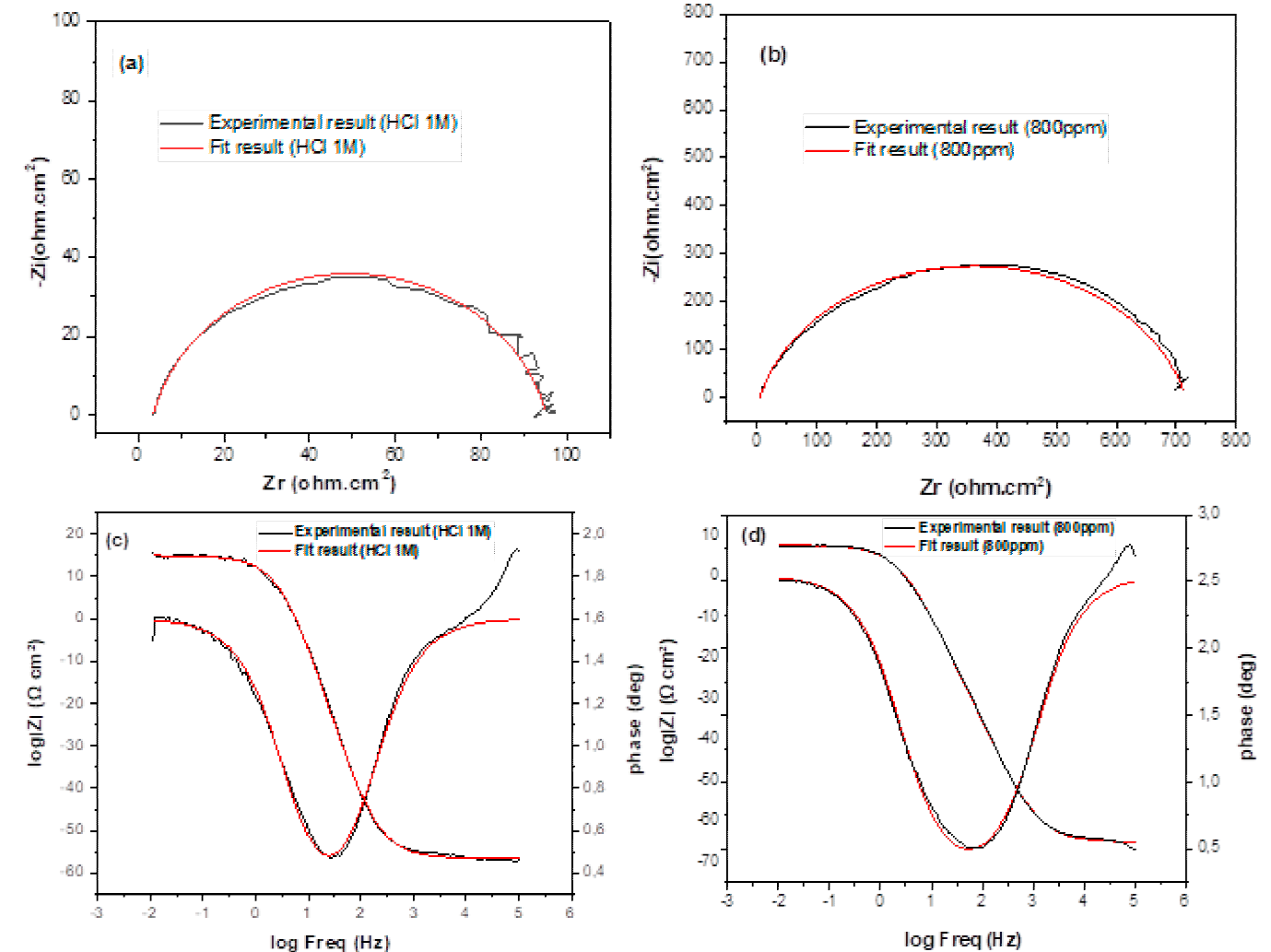
Fig. 7 Simulations of Nyquist and Bode plots based on the equivalent circuit to fit experimental data of EIS in the absence of EBEM (a) and (c) and in the presence of EBEM (b) and (d) at 800 ppm. 

The significance of the temperature on mild steel dissolution in 1 M HCl in the absence and presence of EBEM can be best represented by Arrhenius Equation ^[38]:

Where A is a constant (pre-exponential factor), E_a is the activation energy, R is the universal gas constant and T is the absolute temperature. A plot of the logarithm of the CR versus 1/T showed a straight line. As exhibited in Fig. 8, the values of apparent activation energy E_a obtained from the slope (-E_a/R).

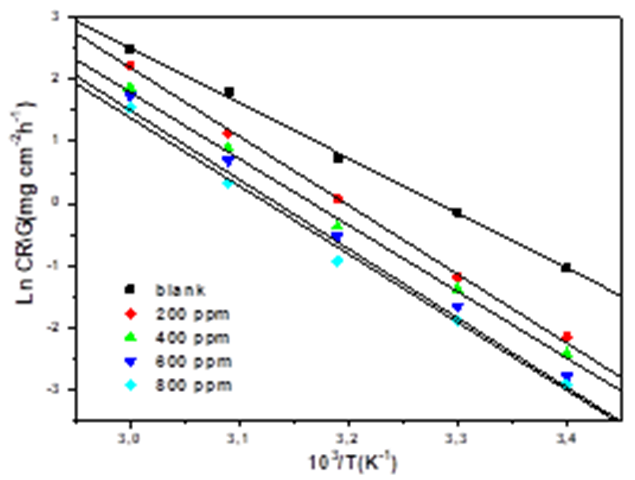
Fig.8. Arrhenius diagram of the corrosion rates of mild steel in 1M HCl medium in the absence and presence of the different concentrations of EBEM. 

The alternative formulation of the Arrhenius relationship (Equation. 9), was employed to calculate the activation enthalpy ΔH_a and activation entropy values ΔS_a^[38, ^44].

In Eq.9, h represents the Planck’s constant and N is the Avogadro’s number. The plot of ln(CR/T) versus 1/T showed a straight line (Fig. 9). The values of ΔH_a and ΔS_a were calculated from the slope (-H_a/R) and intercept (ln(RT/Nh)+(S_a/R).

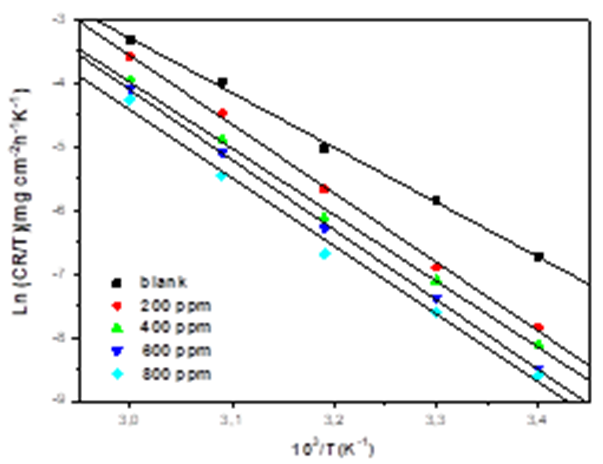
Fig. 9 Alternative Arrhenius diagram of the corrosion rates of mild steel in 1M HCl medium in the absence and presence of the different concentrations of EBEM. 

Activation parameter values for Carbone steel in 1M HCl in the absence and presence of different concentrations of the EBEM enumerated in Table 6.

Investigation of Table 6 reveals the following results:

The values of activation energy were higher in the presence of the EBEM than in its absence. This increase reflects that the inhibitory molecules of EBEM are physisorbed ^[44].

The positive signs of enthalpies reflect the endothermic nature of the dissolution process ^[45,^46].

The entropy values are negative in the free acid solution and positive with the addition of the extract, this suggests that the adsorption of organic inhibitory molecules is accompanied by desorption of water molecules from the surface of steel ^[47].

Adsorption parameters

The adsorption isotherm provides important acquaintance at the interaction of inhibitor and metal surface. It is therefore necessary to know the mode of adsorption. The experimental data were applied according to various adsorption isotherms, notably Freundlich, Langmuir, Frumkin and Temkin. Langmuir adsorption isotherm was best fitted and can be given by the Equation.10.

Where Cinhis the concentration of the inhibitor, K_ads is the equilibrium adsorption constant and θ the surface coverage. According to Fig.10, a straight line (R² > 0.99) was obtained on plotting (C_inh/θ) versus C_inh.

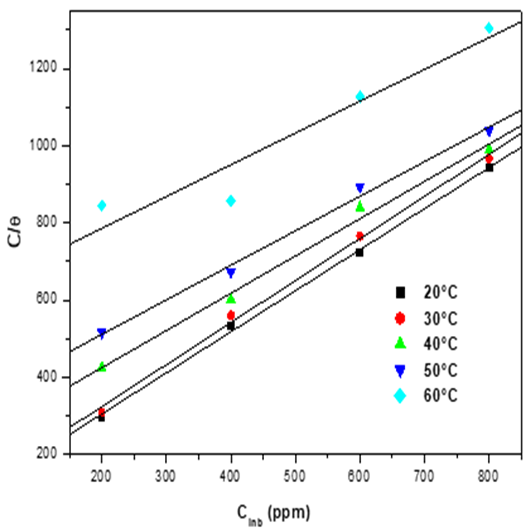
Fig.10. Langmuir adsorption isotherm plots for mild steel in 1M HCl in the presence of EBEM at different temperatures. 

The value of the equilibrium constant K_ads is used to estimate the standard free energy of inhibitor adsorption ∆Gads 0 on the metal surface. This constant can be calculated from the reciprocal of the intercept of the Cinhθ  axis. The following equation is recommended for the calculation of ∆Gads0 at different temperatures.

Where CH2O = 10⁶ mg/L. R is the gas constant and T represents the absolute temperature. The obtained values are summarized in Table 6. In thermodynamic, ∆Gads0is related to the ∆Hads0 and ∆Sads0 of adsorption process. The enthalpy(∆Hads0) and the entropy (∆Sads0) of adsorption process are obtained from the following Equation.12:

Fig.11 exhibits the variation of ∆Gads0 versus T. A straight line is obtained. The slope gives ∆Sads0and the intercept leads to ∆Hads0. The obtained results are scheduled in Table 6.

Fig.11.  Variation of ∆Gads0versus of temperature in 1M HCl. 

Results presented in the Table.7, indicate:

The adsorption and desorption processes of EBEM are in dynamic equilibrium, since constant of adsorption (K_ads) was noticed to decrease with increase in temperature ^[48].

Negative signs of ∆Gads0 reveal the spontaneity of EBEM adsorption on the Carbone steel surface.

The obtained results of the adsorption ΔG_ads values close to −20 kJ/mol confirm the physisorption mechanism ^[49].

The negative sign of ∆Hads0indicates that the adsorption process of EBEM on steel surface is an exothermic one.

The adsorption of inhibitor molecules is accompanied by negative values of ∆Sads0. It might be explained by an ordered layer onto the steel surface ^[50].

Mathematical modeling

Regression is a highly useful statistical technique used in several scientific fields with the aim to develop a quantitative relationship between a dependent variable (response) and one or more independent variables (factors) ^[49]. The least squares method is a statistical standard approach in regression analysis used to find the optimum fit for a set of data points by minimizing the sum of the squares of the residuals of curves points. In this study, two mathematical models were suggested to obtain the best fit between inhibition efficiency (EI_w) of an extract of the plant Ephedra major for mild steel in 1.0 M hydrochloric acid (dependent variable) and independent variables (temperature T and inhibitor concentration C). The developed mathematical models are classified into two groups, linear and polynomial models. Experimental data presented previously were used to construct the models. Both models take into account the individual effect of each variable and the interaction between them. The calculations were done using Matlab Software Program, Version 19.

Linear model

A linear mathematical model was used as a statistical tool aiming to predict the effect of the variables x_i and y_i which are respectively the temperature T(°C) and the inhibitor concentration C (mol/L) as a function z_i which is the inhibitor efficiency (EI_w %). The proposed model is given in the equation bellow:

The optimal parameters a_i within the meaning of the least squares method is those, which minimize the quantity:

In this expression, N is the number of experiments. a_i are constants representing the model parameters. The minimum of this expression is found when the partial derivatives (∂S/∂a_i) are equal to zero:

This leads to the following system of equations:

Parameters of the model were estimated based on the least square method. Since x=T, y=C and z=EI_w. The constants of the model were reported in Table 4.

Polynomial model

The second proposed polynomial model equation was obtained by representing the inhibition efficiency EIw (%) by the response function z which can be expressed by the equation bellow:

Where, x is temperature (°C) and y the concentration (mol/L). Similarly, the optimal parameters a_i within the meaning of the least squares method are those, which minimize the quantity:

The minimum of this expression is obtained using the Equation.15. The expanded equations can be written as:

Constants of the model were estimated and listed in Table 8. Based on both models the predicted values of inhibition efficiency as a function of temperature and inhibitor concentration are computed and gathered in Table 9.

For analysis of the accuracy of the predicted results obtained with linear and polynomial models, the coefficient of determination commonly known as R-squared (or R²), has been estimated using the equation bellow:

In this relationship, z_i are experimental inhibition efficiency, zi~ represents predicted inhibition efficiency and zi- are the average. The determination coefficients were found equal to 0.9325 and 0.9417 respectively, for linear and polynomial models. Figs. 13 and 14 show the relationship between the values of the inhibitor efficiency obtained from the experimental work and those predicted by using both models. It is obvious that almost 80 % and 90 % of the data obtained from the linear and polynomial models located on the line of equality, which means that the experimental and predicted values of inhibitory efficacy are close. This is quite true because the determination coefficients were R²= 0.9325 for linear and R²= 0.9417 for the polynomial model. According to Ref. ^[49], when the correlation coefficient is <0.30 the relationship is weak, between 0.50 and 0.70 it is an important relationship, whereas if it is>0.90 so it is a powerful relationship. Based on correlation coefficients, these results indicate a strong relationship between experimental and mathematical polynomial model. The concordance between the experimental and the predicted results is well seen.

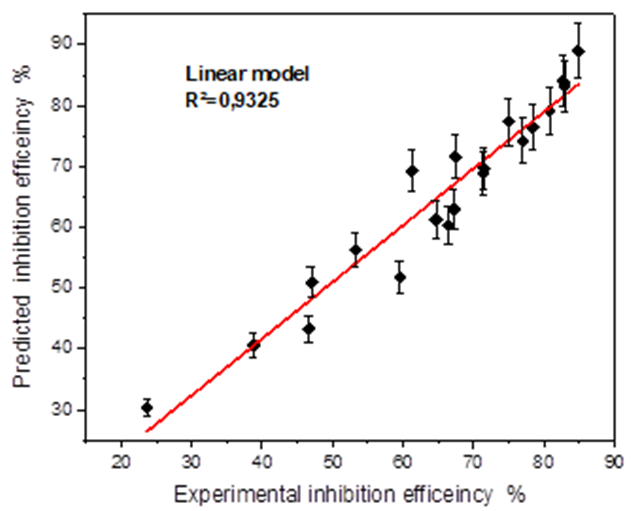
Fig. 13 Fitting curve of experimental against predicated inhibition efficiency obtained by the linear model. 

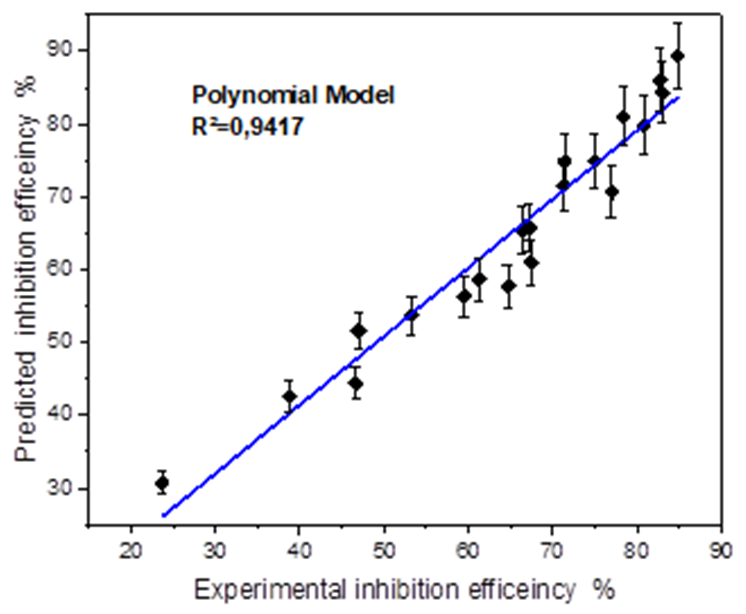
Fig. 14 Fitting curve of experimental against predicated inhibition efficiency obtained by the polynomial model.  

As shown in Fig.15, examination of the data provided by the two models and presented as surface plot, reveals that the addition of butanolic extract of Ephedra major (EBEM), at different concentrations decreases the corrosion rate of mild steel. The inhibition efficiency (IE_W %) increases with increasing inhibitor concentration (red zone) and decreases with increasing temperature (blue zone). This can be explained by a regression of adsorption induced by temperature rise. At concentration 800 ppm and temperature 20 °C, EBEM exhibits maximum inhibition efficiency for both models: 88.95 % (linear model) and 89.35 % (polynomial). A comparison with the experimental value 84.81 % shows the reliability of both polynomial and linear model.

Fig. 15 Surface plot for inhibition efficiency, Temperature and Inhibitor concentration based on: (a) linear model, (b) polynomial model.