Introduction
The North American region, composed of Mexico, the United States, and Canada, signed and implemented an international free trade agreement, the North American Free Trade Agreement (NAFTA), in 1994, following one previously signed by Canada and the United States in 1988. This treaty does not cover labor mobility among countries, although it seeks to deregulate trade in goods and services, as well as capital flows. However, labor is to compete indirectly, that is, through traded goods.
It was expected that factor prices would equalize thanks to international trade.1 This is because free trade by itself would effectively contribute to reducing wage differentials among trade partners. This factor convergence process through foreign trade is the crux of the factor price equalization (FPE) theorem. Originally advanced by Samuelson in 1948, its postulates seem most attractive. By means of free trade, equitable factor payments, in this case regarding labor, would be achieved without the migration requirements involved.
This article empirically examines wage gaps for manufacturing production and nonsupervisory workers in Mexico and the United States both for the manufacturing sector as a whole and also hones in on six selected industries.2 An error correction model provides the econometric method to empirically gauge the manufacturing wage gap.3 I introduce two bilateral determinants in this model: the real exchange rate and the manufacturing production index ratio. These determinants help in estimating the empirical rationale behind the wage gap. The computation of this gap for production workers for Mexico and the United States with respect to selected industries is based on the North America Industrial Classification System (NAICS),4 duly applied for both countries.
This article tests empirically whether the FPE accurately traces the manufacturing wage gap between Mexico and the United States for the pre-NAFTA period of 1987-1994 and two NAFTA sub-periods, 1995-2006 and 2007-2013.5 The results of these estimates could show the intensity by which Mexican competitiveness in manufacturing has been found in the aforementioned gap. In addition, the wage gap leads to unfair competition of Mexico vis-à-vis its northern trade partners. In analyzing the magnitude and pace of this gap, the results provide an array of parameters for reducing that difference through Mexican government intervention in wage settlements.
In estimating a wage gap between Mexico and the United States, this article concentrates on its measurement within the theoretical framework outlined above. The possible reasons that could increase this gap are not considered here. Undoubtedly, several elements could give rise to international wage differentials. For instance, institutional, sociological, and demographic elements could play a key role in determining a possible gap. However, these questions are beyond the scope of this article.
This article is organized as follows: the first section presents a brief review of the literature regarding the theoretical tenets of free trade, as well as empirical studies regarding the wage differentials between Mexico and the United States. The second section shows the behavior of wage gaps through descriptive statistics. The third section estimates the wage differentials through an error-correction econometric model, followed by its results. The fourth section presents my conclusions.
Brief literature review
In the theoretical literature the FPE assumes only two production factors: labor type one and labor type two, in two countries. Labor production factor type one is usually located in a small country, with an abundance of labor as a production factor. Labor production factor type two is usually located in a large country, with a lack of labor as a production factor. The FPE theorem postulates that free international trade would ensure labor factor type one and two payments equalization. If this result holds, then it would imply that labor mobility would be redundant for attaining this outcome.
Regarding the soundness of the FPE theorem, Samuelson (1948) states that factor payments equalization is not only possible and probable, but in a wide variety of circumstances, it becomes inevitable:
As long as there is partial specialization, with each country producing some of both goods, factor prices will be equalized, absolutely and relatively, by free international trade, and
Unless initial factor endowments are too unequal, commodity mobility will always be a perfect substitute for factor mobility.
Samuelson (1948) appears to provide adequate theoretical proof for the foregoing propositions for a two-region, two-commodity, and two-factor case. However, he introduces a caveat in the second proposition: unequal factor endowments could be held responsible for not attaining the wage convergence. As a result, a possible wage differential could be related to a capital-labor gap.
According with Baldwing (2008) the familiar two-country, two-good and twofactor propositions are often referred to as the Heckscher-Ohlin Samuelson (HOS) model. This is in recognition of the contribution made by Samuelson in formulating the Stolper-Samuelson and factor price equalization theorem.
Broadly speaking, the Heckscher-Ohlin theorem could be used for protectionism regarding a specific economic sector. According to Stolper and Samuelson (1941), this theorem assumes that the total amounts of production factors are to remain fixed. In addition, the introduction of trade must lower the relative share in the real or money national income going to the scarce factor of production. Continuing with Stolper and Samuelson (1941), the Heckscher-Ohlin theorem states that the total return to a factor equals its price times the amount employed. They assume full employment both before and after introducing trade. Thus, the total returns to the factors of production are proportional to the rates per unit or marginal productivity. Stolper and Samuelson mention in this regard that if labor is the relatively scarce factor in the U.S. economy, it would appear that trade would necessarily lower the relative position of the working class as compared to owners of other factors of production.
Stolper and Samuelson (1941) consider that Haberley, Wicksell, Carver, Nicholson and others sustain a similar position to the one enunciated by the Heckscher-Ohlin theorem: “If labour enters more importantly in the protected industry, it might possibly be harmed by free trade” (61), and “International trade necessarily lowers the real wage of the scarce factor expressed in terms of any good” (66).
Opinions are divided regarding the Heckscher/Ohlin view, when the Stolper-Samuelson theorem is taken into account. In a nutshell, the latter theorem constitutes a call for universal free trade. For example, Stolper and Samuelson (1941) claim that the Heckscher-Ohlin theorem begins to become less relevant with three or more factors of production, since the ratios of factor prices in the respective countries more closely approach unity.6 Stolper and Samuelson conclude that the HeckscherOhlin theorem does not necessarily hold in the case of constant costs or multiple factors of production.7
The Stolper and Samuelson (1941) analysis assumes two countries, two commodities, two production functions homogeneous of the first order; a known fixed price ratio, , for labor type “one” for a small country in relation to labor type “two” for a large country; full employment before and after any change; and unvarying endowment production factors.8 They also consider the classical cost case of a large country vis-à-vis a smaller country.9 For these two countries the well-known condition of equilibrium of factor prices will be attained through trade. This equilibrium is expressed as the equalization of the ratios of marginal productivities with the ratio of factor prices.
It is also assumed that the first country in question is relatively small and has no influence on the prevailing terms of trade. Also, these authors assume that the removal of duties will not destroy the formerly protected industry, but only force it to enter into a contract. A summary for the case analyzed in this article, taking into account Stolper and Samuelson (1941), is that given by NAFTA, where Mexico and the United States manufacturing labor factor of production of any type in any industry should attain the equalization of marginal productivities and their respective payments thereof.
The basic proposition of the Heckscher-Ohlin theorem is also known as the Rybczynsky theorem (1955).10 This theorem is related to factor endowment and relative commodity prices under the terms of trade. Rybczynsky assumes a closed economy and two factors of production. He proves that maintaining the same rates of substitution in production after the quantity of one factor has increased must lead to an absolute expansion in the production of the commodity using relatively much of that factor, and to an absolute curtailment of production of the commodity using a relatively scant amount of the same factor. He concludes that external terms of trade will deteriorate production. In this sense, Rybczynsky does not foresee any benefit in free trade agreements.
Regarding the specific empirical literature on Mexico and the United States, some researchers have accomplished the task of linking international trade theory and its effect on both wage and income gaps. In what follows, I will briefly review the empirical literature on this topic.
Reynolds (1995), for example, assumes that productivity, factor prices, and wages have a common prior distribution in these two countries. He sees two possible scenarios after the implementation of NAFTA: the first is an upward convergence for the wage gap, implying that those starting at the low end of the distribution will move up toward those at the high end of the distribution. Thus, those at the high end of the distribution do not descend. The second possible scenario is less favorable, as it comprises a downward convergence. This could happen when wages increase modestly at the low end of the distribution and wages at the high end decrease toward the low end.
For their part, Peach and Adkisson (2002) look at whether there has been an income convergence between the United States and Mexico. They give the following income figures: US$34,950 as the per capita gross domestic product (GDP) from 2000 for the United States.11 The corresponding figure for Mexico was US$5,720 in 2001.12 The difference between the two countries, in terms of dollar per capita GDP was over six-fold after six years of NAFTA coming into effect. Both Peach and Adkisson restate findings by Samuelson (1949; 1971) and Mundell (1957), whose theoretical free trade framework was used to explain income convergence. When Peach and Adkisson (2002) do not empirically observe wage convergence, they explain income divergence as the result of institutional rigidities, which in turn cause market failures.13 They mention that Mexico attained its highest income per capita GDP when market-oriented policies were at their weakest. Paradoxically, these policies are the result of government intervention, regarded as the principal cause for market failures according to their theoretical assumptions. They also point out the following conundrum: when market-oriented policies were weakest, the two countries registered the highest income convergence. As a result, these authors acknowledge the income gap as a most important policy issue.
The wage gap empirical analysis takes on a different dimension for Robertson (2005). He investigates labor market integration between Mexico and the United States considering two periods, before and during NAFTA. He uses different approaches to accomplish this task, for example, measuring the responsiveness of Mexican wages to wage shocks in the United States. He explains this responsiveness in two ways: i) the speed at which relative wages return or do not return to a long-run differential, and ii) the absolute wage convergence growth rate. Robertson uses a wage equation with data generated from a pseudo-panel technique, as well as data collected from the Mexican National Survey of Urban Employment and the United States Current Population Survey. His econometric results suggest that trade variables (measured as exports plus imports) and foreign direct investment do in fact positively contribute to labor market integration. At the same time, he finds that border policy enforcement depresses Mexican wages. In his view, border enforcement could mask the positive benefits of market integration. It is important to note that Robertson (2004) uses relative wages: that is, the wage rate of hourly weighted employment of i) non-production to ii) production workers.
In a discussion paper, Gandolfi, Halliday, and Robertson (2014) find no evidence of long-run factor price convergence for the period of 1988-2011. For this analysis, they consider population cohorts characterized by low migration propensities. These authors try to explain this apparent contradictory result using neoclassical trade theory, arguing that major macroeconomic shocks such as the 1994 Mexican peso crisis are the culprits. They use two complementary methodologies. The first is applied to survey data with a synthetic panel approach and an econometric analysis. The second methodology uses descriptive statistics, resorting to census information from each decade, namely, 1990, 2000, and 2010.14
From the foregoing literature review, it is clear that income gap or wage gap analysis between Mexico and the United States has not definitely been identified as converging or narrowing since NAFTA implementation. In fact, evidence for this identification is nil or, at best, inconclusive.
Data
Three discontinuous longitudinal data sets on Mexican wages and output are available, based on official manufacturing surveys. In the case of Mexico, the data set is discontinuous, since the national statistics office enlarged the industry sample size, from 205 industrial activities up to 240 for the last period of 2007-2013.
On the basis of the above data availability, I selected three different non-overlapping monthly time periods for econometric estimation. The first is pre-NAFTA, from January 1987 to December 1994 (1987: 01-1994: 12); the second and third are from the NAFTA time period, containing two sub-periods: from January 1995 to February 2006 (1995: 01-2006: 02) and from January 2007 to December 2013 (2007: 01-2013: 12).
I selected the manufacturing industries reported in Table 1 on the basis of their importance in total Mexican exports.15 Also, these industries are arranged according to United States manufacturing goods classification for non-durable and durable goods. Consequently, the selected non-durable industries are i) food; ii) textile products and mills, and iii) chemicals. The durable industries are iv) primary metal; v) machinery; and vi) transportation equipment.
Table 1 Descriptive statistics. Wage gap trends. Manufacturing production workers in Mexico and the United States (selected periods and industries)
| Sector of Industry | Statistic | Pre-NAFTA | NAFTA | |
| 1987: 01-1994: 12 | 1995: 01-2006: 12 | 2007: 01-2013: 12 | ||
| Manufacturing | mean | 0.15 | 0.14 | 0.11 |
| cv | 0.29 | 0.23 | 0.12 | |
| Food | mean | 0.14 | 0.17 | 0.10 |
| cv | 0.30 | 0.24 | 0.13 | |
| Textile | mean | 0.18 | 0.16 | 0.12 |
| Products and Mills | cv | 0.30 | 0.28 | 0.17 |
| Chemicals | mean | 0.15 | 0.14 | 0.19 |
| cv | 0.31 | 0.24 | 0.20 | |
| Primary Metal | mean | 0.14 | 0.14 | 0.13 |
| cv | 0.25 | 0.19 | 0.09 | |
| Machinery | mean | 0.14 | 0.15 | 0.13 |
| cv | 0.32 | 0.26 | 0.11 | |
| Transportation Equipment |
mean | 0.12 | 0.15 | 0.09 |
| cv | 0.31 | 0.30 | 0.12 | |
| n | 96 | 144 | 84 | |
Note: Adjusted for inflation with the producer price index (finished goods); not seasonally adjusted; mean stands for the first moment of the time series; cv stands for the coefficient of variation; n stands for the number of observations.
Source: The author’s own estimates based on data from Banco de Mexico, the U.S. Bureau of Labor Statistics, and the Instituto Nacional de Estadística y Geografía.
In this article, the wage gap for manufacturing is defined as the ratio of the Mexican wage divided by the U.S. wage, both expressed in dollar terms.16 Thus, the wage gap could be read as follows: the number of dollars paid on average per hour for a Mexican manufacturing worker in relation to the dollars paid on average per hour for his/her U.S. counterpart. Workers in the selected industries are considered to perform similar industrial tasks and economic activities are classified using a common North American Industrial Classification System (NAICS).17 If the wage gap were equal to one, it would imply that Mexican and U.S. workers receive equal labor compensation. This hypothetical value would indicate a wage gap absence. If the wage gap approaches zero, it would indicate that labor compensation is approaching a maximum divergence between these two countries.
Descriptive statistics
I examine the principal trends of the wage gap under study by means of descriptive statistics. Table 1 presents the wage gap mean (first moment of a distribution) and cv (coefficient of variation) for the whole manufacturing sector and six selected industries, considering pre-NAFTA and the NAFTA sub-periods.
Table 1 illustrates that the mean wage gap for the whole manufacturing sector between Mexico and the United States has increased across time, that is, 0.15, 0.14, and 0.11. As a result, the wage gap has grown, despite NAFTA implementation. By contrast, the whole manufacturing sector cv has decreased across the three time periods analyzed. That is, it exhibits values of 0.29, 0.23, and 0.12. These cv values imply that the wage gap has gained stability over time, suggesting a long-run trend of wage gap increases during the NAFTA period.18
For the pre-NAFTA period (1987-1994), the wage gap in chemicals remains equal to the manufacturing mean, with a reported value of 0.15. For this same time period, the textile products and mills mean is 0.18. Four manufacturing sectors are below the manufacturing mean: food, primary metal, machinery, and transportation equipment, with values of 0.14, 0.14, 0.14, and 0.12, respectively. For its part, the cv for all industries assumes values along the range of 0.25 to 0.31 for this time period.
By comparing the two NAFTA time sub-periods, 1995-2006 and 2007-2013, to the previous period, it is clear that both mean and cv patterns for all industries under study have similar decreasing rates trends. The only exception is the chemicals sector, which increases its wage gap mean from 0.14 to 0.19. From 2007 to date, only food and transportation equipment exhibit a mean wage gap below manufacturing. Meanwhile, the rest of the industries show wage gap means ranging between 0.12 and 0.13. Overall, Table 1 indicates an increase in the wage gap during the last period, with the exception of chemicals.19 During the third period, the cv for all industries decreased with respect to the two previous periods. That is, the cv for all industries under consideration fell by more than half between 2007 and 2013, indicating continuity in this process.
Figure analysis
An almost parallel movement exists between the bilateral real exchange rate and the wage gap (Figure 1). This bilateral real exchange rate for Mexico and the United States is computed as the ratio of U.S. and Mexican consumer prices divided by the nominal exchange rate, that is, pesos per dollar. This parallel movement shows that a real exchange rate overvaluation is accompanied by a wage gap reduction and vice versa: when the bilateral real exchange rate depreciated, the wage gap increased.20 An example of this last case can be easily observed in December 1994, when the Mexican peso depreciated from 0.035 to 0.02, as measured by the Mexican and U.S. real exchange rate. As a result, the wage gap registered an increase from 0.15 to 0.09. In the same way, the 2009 Mexican peso depreciation matched with a high wage gap value of 0.08. In the opposite way, when the real exchange rate was overvalued around 2002, the wage gap registered its lowest value during the NAFTA period, that is, 0.25. Insofar as changes in the wage gap follow changes in the bilateral real exchange rate, this last economic indicator is included as one of the determinants in the econometric model.21
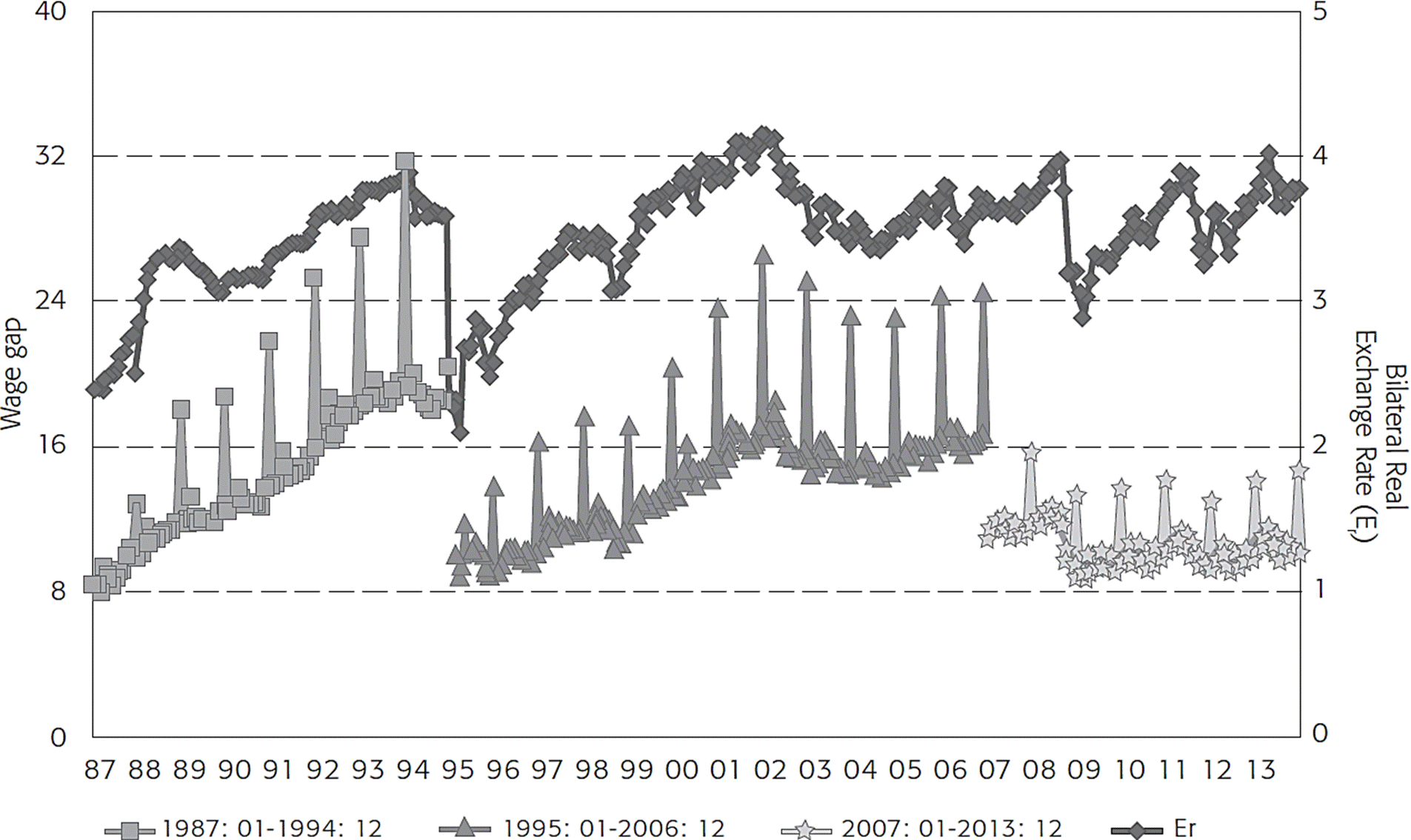
Source: The author’s estimates based on data from Banco de México, the Bureau of Labor Statistics, and the Instituto Nacional de Estadística y Geografía.
Figure 1 Wage gap and bilateral real exchange rate. United States-Mexico. Total manufacturing production workers. Monthly frecuency. Selected periods
Figure 1 illustrates a wage gap trend decrease, taking into account each time period, from 1987-1994 to 1995-2006 and from 1995-2006 to 2007-2013. That is, the lines that represent the wage gap have a diminished slope over time, tending toward zero.
As a brief summary of the figure analysis sub-section, the wage gap increases and cv decreases over time. These trends did not happen immediately after NAFTA was enacted. It took 12 years after the agreement was signed for the manufacturing activities of both nations to reflect trend changes in the wage gap. These shifts are presented in both wage gap increases as well as in a stability increase in this trend. These changes demonstrate that a structural change took place as a result of the government intervention through NAFTA. Nevertheless, this pattern took 12 years to materialize. In addition, the wage gap descriptive statistics regarding mean and cv and their graphic trends did not conform to the expected free international trade theory outcomes. The latter are a main tenet of the FPE.
Econometric model
In this section, I put forward the derivation of the econometric model. This model basically sets the production workers’ manufacturing wage gap for Mexico and the United States in dollar terms as a function of a bilateral Mexico-United States real exchange rate,22 and a manufacturing production index. Thus, the econometric equation proposed is
where
The superscript i in Equation (1) expresses the time period under consideration, taking the following values: i = 1, 2, 3, where i=1 covers from January 1987 to December 1994; i=2 stands for January 1995 to December 2006; i=3 spans January 2007 to December 2013.24 The subscript k refers to the manufacturing sector as a whole, as well as for the industries selected, that is, k=1 for total manufacturing. The six selected industries can be classified in non-durable and durable goods following international guidelines.25 Thus, non-durable goods industries are made up of k=2, food; k=3, textile products and mills; and k=4, chemicals. For their part, durable goods are k=5, primary metal; k=6 machinery; and k=7, transportation equipment. The subscript refers to the current time period; t - j signals time lags, where j = 1, 2, …, n. The subscript mx refers to Mexico and us to the United States.26
It is important to note that if the law of one price holds, then Equation (1) is reduced to two ratios. One of these ratios is in the left-hand side and the other in the right-hand side of this equation. Thus, Equation (1) would equal these two ratios, that is, numerator to numerator and denominator to denominator, after the elimination of the bilateral real exchange. If this were the case, factor compensations (left side) would be equal to manufacturing production index (right side). Thus, this equation could be a representation of Shepard’s lemma in equilibrium: labor payments are proportional to their productivities, an assumption in the FPE theorem.27
If the law of one price does not hold, then the inclusion of the bilateral real exchange rate between Mexico and the United States seems necessary. According to Samuelson (1994), the Penn effect consists of the presence of exaggerated income ratios between countries and the need to use conventional exchange-rate conversions. In this sense, the inclusion of the manufacturing index ratio in Equation (1) also has a practical rationale.28
For their part, Lawrence and Slaughter (1993) argue that the empirical performance of average real wages in an international trade framework is expected to mirror the performance of output per worker. In the same fashion, Burgman and Geppert (1993) claim that if the FPE holds, marginal productivity and real wages must become equal across economies.
Conforming to the information laid out in this section, the expected values or theoretical hypothesis for the estimators in Equation (1), are as follows: is expected to have a value close to zero if the FPE holds; is expected to be positive and unitary if Shepard’s lemma is fulfilled.29
Error correction model empirical results
Equation (1) is estimated for the three monthly time periods, pre-NAFTA (1987-1994) and NAFTA (1995-2006 and 2007-2013), for the whole manufacturing sector and six selected industries. For simplicity’s sake, these three time periods will be referred to in what follows as the first, second, and third periods, respectively. To facilitate Equation (1) interpretation, its estimators are grouped in two different tables, Tables 2 and 3. Table 2 displays the bilateral real exchange rate estimators and Table 3 reports the manufacturing production index ratio estimators.30
Table 2 Bilateral real exchange rate (Er) between Mexico and the United States, Equation (1) results (selected periods and industries) (standard error) [lag]
| Sector of industry | Pre-NAFTA | NAFTA | |
| 1987: 01-1994: 12 | 1995: 01-2006: 12 | 2007: 01-2013: 12 | |
| Manufacturing | |||
| Long run | 1.60 (0.1607)[1] | 1.40 (0.0993)[0] | 0.80 (0.1306)[0] |
| Short run | 1.08 (0.7412)[1] | 1.33 (0.3324)[0] | 0.87 (0.2553)[0] |
| Food | |||
| Long run | 2.45 (0.1386)[1] | 1.06 (0.0889)[0] | 1.12 (0.1486)[0] |
| Short run | 2.89 (1.3576)[1] | 1.06 (0.3257)[0] | 0.94 (0.2169)[0] |
| Textile products and mills | |||
| Long run | 1.71 (0.2751)[1] | 0.48 (0.1794)[0] | 0.64 (0.2293)[0] |
| Short run | 1.65 (0.3551)[1] | 1.13 (0.4620)[0] | 0.78 (0.4565)[0] |
| Chemicals | |||
| Long run | 1.97 (0.1019)[1] | 1.30 (0.0984)[0] | 0.51 (0.2858)[1] |
| Short run | 1.37 (0.5664)[1] | 1.21 (0.3232)[0] | 0.85 (0.5220)[1] |
| Primary metal | |||
| Long run | 1.95 (0.2490)[1] | 1.03 (0.0939)[0] | 0.75 (0.1093)[0] |
| Short run | 1.96 (0.0876)[1] | 1.26 (0.1920)[0] | 0.83 (0.2104)[0] |
| Machinery | |||
| long run | 1.76 (0.3045)[1] | 1.19 (0.1096)[0] | 0.96 (0.1231)[0] |
| short run | 2.18 (0.0703)[1] | 1.39 (0.3545)[0] | 1.05 (0.3643)[0] |
| Transportation Equipment | |||
| Long run | 1.79 (0.2761)[1] | 1.09 (0.1614)[0] | 1.22 (0.1323)[0] |
| Short run | 1.93 (0.1323)[1] | 1.78 (0.4109)[0] | 0.77 (0.2335)[0] |
| 96 | 144 | 84 | |
Note: The bilateral real exchange rate between Mexico and the United States is computed based on the consumer price index; n stands for the number of observations. For brevity the constant is not reported; no dummy variable was required for modeling the year-end aguinaldo payment. All reported elasticities are statistically significant at least by 95 percent; long- and short-run equations are computed using ordinary least squares in a two stages procedure, following Sargan (Hendry and Wallis, 1984).
Source: The author’s own estimates based on data from the Banco de Mexico, the Bureau of Labor Statistics, and the Instituto Nacional de Estadística y Geografía.
Table 3 Manufacturing production index ratio
| Sector of industry | Pre-NAFTA | NAFTA | |
| 1987: 01-1994: 12 | 1995: 01-2006: 12 | 2007: 01-2013: 12 | |
| Manufacturing | |||
| Long run | 1.05 (0.2762)[1] | -1.72 (0.3332)[0] | -1.08 (0.1618)[0] |
| Short run | 0.7 (0.2644)[1] | -1.62 (0.2497)[0] | -1.25 (0.1890)[0] |
| Food | |||
| Long run | 0.41 (0.2287)[1] | 1.82 (0.1740)[1] | -1.00 (0.2771)[3] |
| Short run | n.s. | -0.64 (0.2684)[1] | -0.70 (0.2501)[3] |
| Textile products and mills | |||
| Long run | -0.46 (0.2615)[0] | 0.67 (0.1447)[1] | -0.20 (-0.4023)[3] |
| Short run | -1.17 (0.1374)[0] | -0.49 (0.1630)[0] | -0.56 (0.1555)[3] |
| Chemicals | |||
| Long run | 1.37 (0.2808)[1] | -1.47 (0.1883)[0] | -0.56 (0.3533)[3] |
| Short run | 0.79 (0.2483)[1] | -1.45 (0.1435)[0] | -0.47 (0.3109)[3] |
| Primary metal | |||
| Long run | 0.63 (0.2369)[1] | 0.32 (0.0879)[3] | -0.35 (0.1251)[0] |
| Short run | 0.52 (0.1952)[1] | -0.58 (0.1104)[3] | -0.43 (0.1311)[0] |
| Machinery | |||
| Long run | 0.38 (0.1363)[3] | -0.33 (0.0979)[0] | -0.27 (0.0509)[0] |
| Short run | -0.66 (0.1924)[0] | -0.46 (0.0903)[3] | -0.44 (0.1466)[0] |
| Transportation equipment | |||
| Long run | 0.52 (0.1017)[1] | 0.52 (0.1229)[2] | -0.40 (0.0929)[0] |
| Short run | 0.46 (0.1016)[1] | -0.32 (0.1474)[2] | -0.66 (0.0739)[0] |
| 96 | 144 | 84 | |
Note: Manufacturing production index ratio between Mexico and the United States adjusted for local implicit price indexes; n stands for the number of observations; n.s. stands for not significant. For the sake of brevity, the constant is not reported; no dummy variable was needed for modeling the year-end aguinaldo payment. All reported elasticities are statistically significant by at least 95 percent; long- and short-run equations are computed using ordinary least squares in a two stages procedure, following Sargan (Hendry and Wallis, 1984).
Source: The author’s own estimates based on data from Banco de Mexico, the Bureau of Labor Statistics, and the Instituto Nacional de Estadística y Geografía.
The bilateral real exchange rate between Mexico and the United States
Table 2 reports long- and short-run results for Equation (1) with respect to the bilateral real exchange rate between Mexico and the United States. For the long run, the manufacturing elasticity coefficient reports a value of 1.60 during the first period.31 For the last period, the coefficient almost halved (0.80) with respect to the second period (1.40). In the short run, for the first two periods, the estimators are elastic (1.08 and 1.33, respectively), while attaining a value below the unit (0.87) during the third period. The result for the manufacturing sector as a whole is replicated for the rest of durable industries under consideration: primary metal; machinery, and transportation equipment, with the exception of machinery for the short run (1.05).
For its part, food reaches large coefficients, above two units (2.45 and 2.89 for the long and short run, respectively) during the first period.32 It falls to a value around one in the second and third periods. While this reduction phenomena for the first period is replicated in textile products and mills and chemicals sectors, with coefficients approaching two units in the long and short run in the first period, in the third period they become clearly inelastic in the long run (0.64 and 0.51, respectively for these two industries)33 and elastic but below one (0.78 and 0.85, respectively) in the short run.
Above, the bilateral real exchange rate effect in the wage gap is measured by its elasticity coefficients. In summary, all of them display positive elasticities, frequently in the vicinity of the unit value. Therefore, it could be confirmed that a Mexican peso undervaluation vis-à-vis the U.S. dollar have the effect of increasing the wage gap.34 From these results, the bilateral real exchange rate is a decisive determinant regarding wage gap performance.
Manufacturing production index ratio between Mexico and the United States
As shown in Table 3, during the third time period, 2007-2013, the manufacturing production index ratio between Mexico and the United States (manufacturing production index ratio) persistently displays negative coefficients regarding the wage gap between Mexico and the United States. As an example, during this period, food has an elastic coefficient in the long run of -1.00, and in the short run it is reduced to -0.70.35 Textile products and mills show negative and inelastic coefficients for the long (-0.20) and (-0.56) short run.36 It should be noted that this industry is the only one that displays negative coefficients for the first time period: -0.46 and -1.17 for the long and short run, respectively. Machinery also has a negative coefficient in the first period (-0.66), although this behavior is restricted for the short run. For the remaining industries, this coefficient has turned from positive in the pre- NAFTA period to negative in the two NAFTA sub-periods.
Negative coefficients during the last NAFTA period are neatly displayed in different industries. For its part, chemicals had negative and inelastic coefficients in the long (-0.56) and short (-0.47) run for the third period.37 Likewise, primary metal had inelastic and negative elasticities in the long and short run (-0.35 and -0.43, respectively) in the third period. For this period, machinery is a similar case, with reported elasticities of -0.27 and -0.44 for the long and short run, respectively. Similarly, this trend is shown for transportation equipment, with negative coefficients of -0.40 and -0.66 in the long and short run, respectively. In this third period, manufacturing displays likewise as the six selected industries’ negative and elastic coefficients, -1.08 and -1.25, for the long and short run, respectively.
At least for NAFTA periods, the increase in the manufacturing output index ratio negatively affected the wage gap, with a coefficient fast approaching the unit. Specifically, in the long run, manufacturing and food exhibit a coefficient value of -1.08, and -1.00, respectively. When manufacturing is disaggregated into durable and non-durable goods, their short-run elasticities coefficients frequently become inelastic and close to half the unit for the three time periods under consideration. In the long run, their elasticities coefficients basically display positive values for the pre-NAFTA period, changing to negative in both NAFTA periods. That is to say, these values of the estimators change from the pre-NAFTA to the NAFTA periods. This change indicates that the government intervention that took place due to NAFTA did bring as a result a structural change in the manufacturing performance of both Mexico and the United States.
The theoretical hypotheses regarding the values of the coefficients and of Equation (1) are not observed, given the empirical results. This is because the FPE hypothesis of a zero coefficient for the bilateral real exchange rate is not fulfilled. In the same manner, the Shepard’s lemma hypothesis of a unitary positive coefficient is far from being observed.
In contrast to the foregoing results, other studies analyzing income and wage gaps for the case of Mexico and the United States have not definitely identified a wage gap convergence or narrowing as result of NAFTA implementation. In fact, evidence for income or wage gap equalization is inconclusive. For instance, Reynolds (1995) claims that for the wage distribution of Mexico and the United States, the analyst can be on one of the extremes, but never at the center. Peach and Adkisson (2002) do not observe wage convergence based on balance-of-payment figures. For Robertson (2005), border policy enforcement depresses Mexican wages, masking the positive effects of market integration. Gandolfi, Halliday, and Robertson (2014) argue that major macroeconomic shocks such as the 1994 Mexican peso crisis are the culprits for not attaining wage convergence.
A robustness check can be performed on Tables 2 and 3 because the Equation (1) estimation includes different time periods and manufacturing industries. Across these specifications, the estimated coefficients behave systematically. This behavior is manifest since all reported coefficients are closely related with respect to the value of the estimators reported. All of these estimators attain a statistical significance level of at least 95 percent. Therefore, the econometric model sensitivities under different specifications, that is, time periods and manufacturing industries, prove to be statistically robust. Structural changes, for example, the one represented by NAFTA government intervention, cause modifications in the signs and values of the estimators. However, these modifications turn out to be stable across manufacturing industries and time periods once the structural change took place after a period of 12 years. The existence of a true economic relationship in the error correction model is confirmed by long-run stationary cointegrating errors. The cointegrating equilibrium errors unit root tests are reported in Appendix 3, and the Johansen cointegration test results are reported in Appendix 1. Together, these two tests support the existence of a true economic relationship between the economic indicators used in Equation (1).
A bilateral real exchange rate between Mexico and the United States is computed considering consumer price indexes for both countries as well as the nominal exchange rate. The latter is used for estimating Mexican peso vis-à-vis the U.S. dollar appreciation or depreciation.38
The formulation of Equation (1) takes into account the empirical results, where the bilateral real exchange rate is a decisive determinant regarding wage-gap performance. In addition, the manufacturing production index ratio for Mexico and the United States is introduced in the econometric model as a wage-gap determinant. Its importance is extracted from Shepard’s lemma implications, where factor compensations are proportional to their productivities.
Conclusions
The sizable manufacturing wage gap between Mexico and the United States continues to expand.39 Descriptive statistics expose the persistence of a manufacturing wage gap increase over time. On average for the pre- NAFTA period 1987-1994, a Mexican worker earned 15 percent of that earned by his United States counterpart. This differential increased from 2007 to 2013, while the proportion fell to 11 cents on the dollar. Hence, during the first period, on average, Mexican manufacturing wages were almost one-seventh of what their U.S. counterparts were earning. During this last period, the difference grew to close to one-tenth.40
The empirical evidence presented in terms of descriptive statistics, figure analysis, and long- and short-run estimators make it clear that the bilateral real exchange rate between Mexico and the United States and the manufacturing production index ratio are relevant, decisive empirical determinants in the wage gap for manufacturing production and nonsupervisory workers between Mexico and the United States.
The wage gap process shows a persistent pattern with a diminishing trend during the three periods under analysis, as expressed with a decreasing coefficient of variation. The wage gap increased once NAFTA was implemented, as attested in the descriptive statistics through a decreasing mean.
The elasticity coefficients obtained between the wage gap and the bilateral real exchange rate regarding Mexico and the United States display a systematic relationship. This is represented by frequently elastic coefficients with positive values. These results convey the meaning that changes in the bilateral real exchange rate are transmitted almost completely to the wage gap. Thus, undervaluation of the Mexican peso with respect to the U.S. dollar increases the wage gap, but with lesser intensity as time goes on. This is attested to as the coefficient of variation displays a persistent diminishing trend.
The wage gap trend follows the bilateral real exchange trend. In addition, their coefficient values are elastic and positive. Therefore, it follows that a relationship exists between the bilateral real exchange undervaluation and the wage gap widening over time.
During the last NAFTA sub-period, a negative relationship was reported between the wage gap and the manufacturing production index ratio. It is important to note that for this NAFTA period, the descriptive statistics show an increase in the wage gap. Therefore, these two results together indicate that the manufacturing production index ratio increases have a deleterious effect on the wage gap. Finally, the FPE theorem does not hold regarding the wage gap between Mexico and the United States.











 nueva página del texto (beta)
nueva página del texto (beta)



