Introducción
Las columnas circulares de concreto reforzado son utilizadas ampliamente alrededor del mundo en una gran cantidad de construcciones (edificios, puentes, cimentaciones). Ahora bien, dos principales ventajas respecto a las columnas rectangulares: a) simplicidad de construcción, b) resistencia y rigidez idéntica para cualquier dirección de análisis ante fuerzas laterales provocadas por sismos, viento, presión de tierra, etc. (Cosenza et al., 2011) (figura 1).
Sin embargo, la complejidad del diseño ante flexión y compresión respecto a secciones rectangulares o cuadradas aumenta; una opción simplificada en el cálculo del diagrama de interacción es proponer un anillo continuo para sustituir la distribución puntual del acero de refuerzo longitudinal (ACI, 2015; Di Laora et al., 2019; Quaranta et al., 2017). Esta hipótesis influye en los resultados y tiene mayor importancia si existen pocas barras verticales (Tayem y Najmi, 1996; Kent, 2012). Según Wight y Macgregor (2012), el error es despreciable cuando se utilizan al menos 8 barras.
Si bien existen aplicaciones para el cálculo del diagrama de interacción en columnas circulares desarrolladas mediante integración numérica, procedimiento iterativo, funciones de forma cerrada (Hernández y Sotolongo, 2018; Hernández-Montes et al., 2005), ninguna utiliza la ubicación real de acero de refuerzo vertical. En este sentido, tampoco existe información sobre el error generado.
Este artículo presenta una formulación matemática que evalúa la influencia de la distribución del acero de refuerzo longitudinal en los diagramas resistentes de interacción de columnas sólidas circulares sin efectos de esbeltez. Así, se analiza la diferencia entre dos diagramas de una columna con características definidas para dos diferentes posiciones de las barras de refuerzo y se determina la cantidad mínima que reduzca el error a un valor predefinido. También se calculan dos series de diagramas resistentes a partir de la posición real de las barras de refuerzo en columnas con 6 y 8 barras.
1. Metodología
1. 1. Cálculo del diagrama de interacción nominal
El comportamiento de los elementos de concreto sometidos a flexión se basa en las siguientes hipótesis (ACI, 2019): a) la deformación del acero es proporcional a la distancia del eje neutro, b) el concreto no resiste esfuerzos de tensión, c) la máxima deformación en la zona extrema a compresión del concreto es εc = 0.003 y el bloque idealizado de compresión del concreto tiene forma rectangular con intensidad igual a 85% de la resistencia a compresión.
La figura 2a muestra la geometría de una columna sólida con diámetro R y peralte d. El centroide de la capa de acero longitudinal está a una distancia r del borde exterior. La deformación de la fibra extrema superior del concreto es εc y la deformación máxima del acero en tensión es εst ; en este caso, se supone que existen cuatro barras de acero, donde la superior está a una distancia zi de la fibra de máxima compresión y presenta una deformación εsi . El ángulo β se mide entre el eje vertical y la primera barra de acero colocada a la derecha y en el caso crítico es la mitad del ángulo entre barras (θ).
El cálculo del diagrama de interacción se realizó de acuerdo con ACI (2020), para lo cual se define el parámetro Z adimensional con valor inicial igual a uno; la deformación extrema εst se evalúa con la ecuación 1, donde εty es la deformación de fluencia igual a 0.002. La profundidad del eje neutro (c) y del bloque idealizado de esfuerzos (a) se evalúan con las ecuaciones 2 y 3. El factor β 1 es función de la resistencia a compresión.
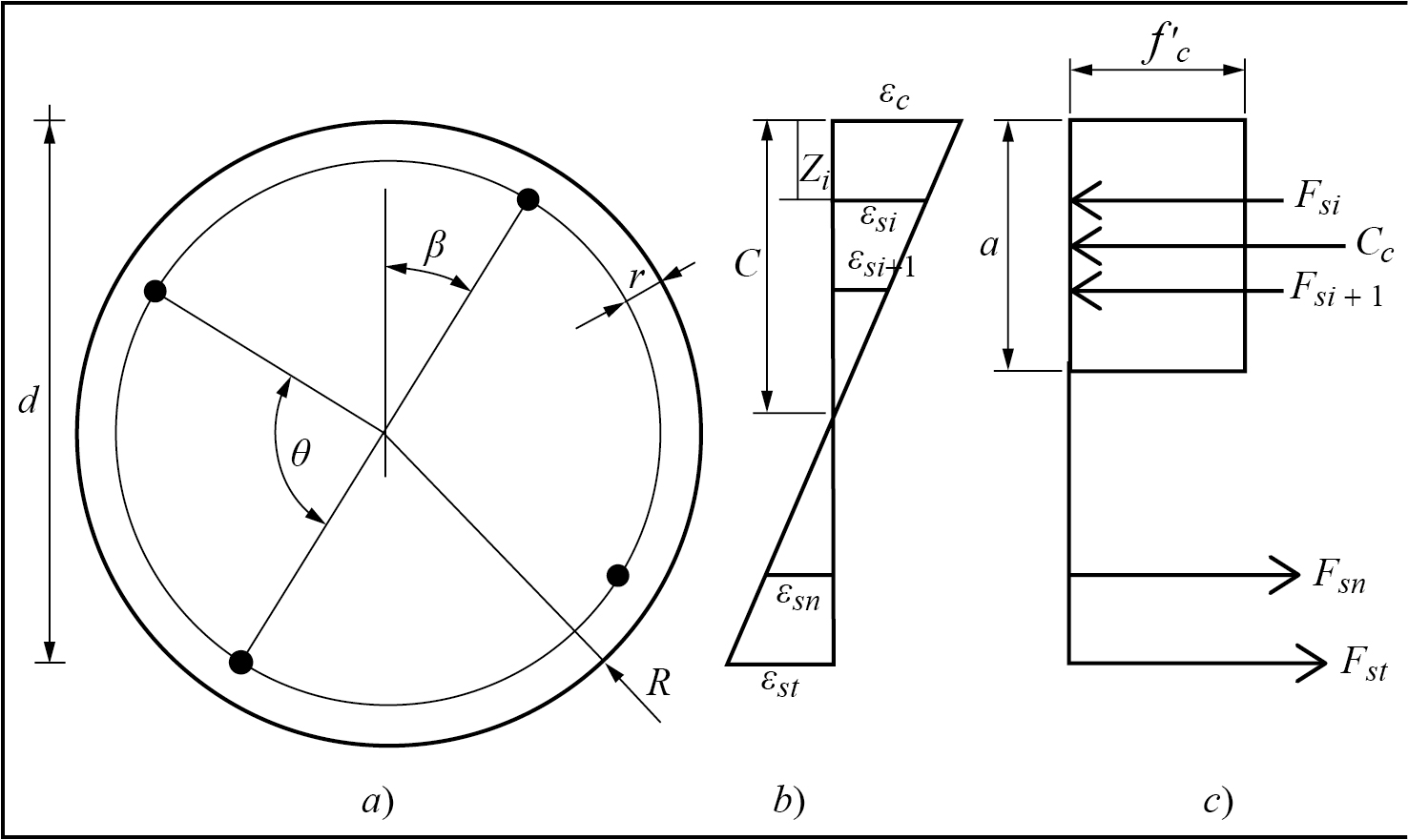
Fuente: elaboración propia. Nota: a) Geometría de columna y distribución de acero longitudinal, b) diagrama de deformaciones, c) diagrama de esfuerzos
Figura 2 Geometría de una columna sólida
De acuerdo con la geometría de la sección, existen dos condiciones para evaluar la compresión del concreto relacionadas con la relación a/R, inciso a o b de la figura 3. En el primer caso hay dos superficies en compresión (A 1 y A 2) y una en tensión (A 3): la primera y tercera se evalúan con las ecuaciones 4 y 5 y la segunda se obtiene por diferencia entre estas expresiones, ecuación 6. Las ecuaciones 7 y 8 evalúan los centroides y 1 e y 3, mientras que la ecuación 9 define el centroide y 2 (AMDROC, 2006). La fuerza total de compresión y el momento se calculan con las ecuaciones 10 y 11 respectivamente.
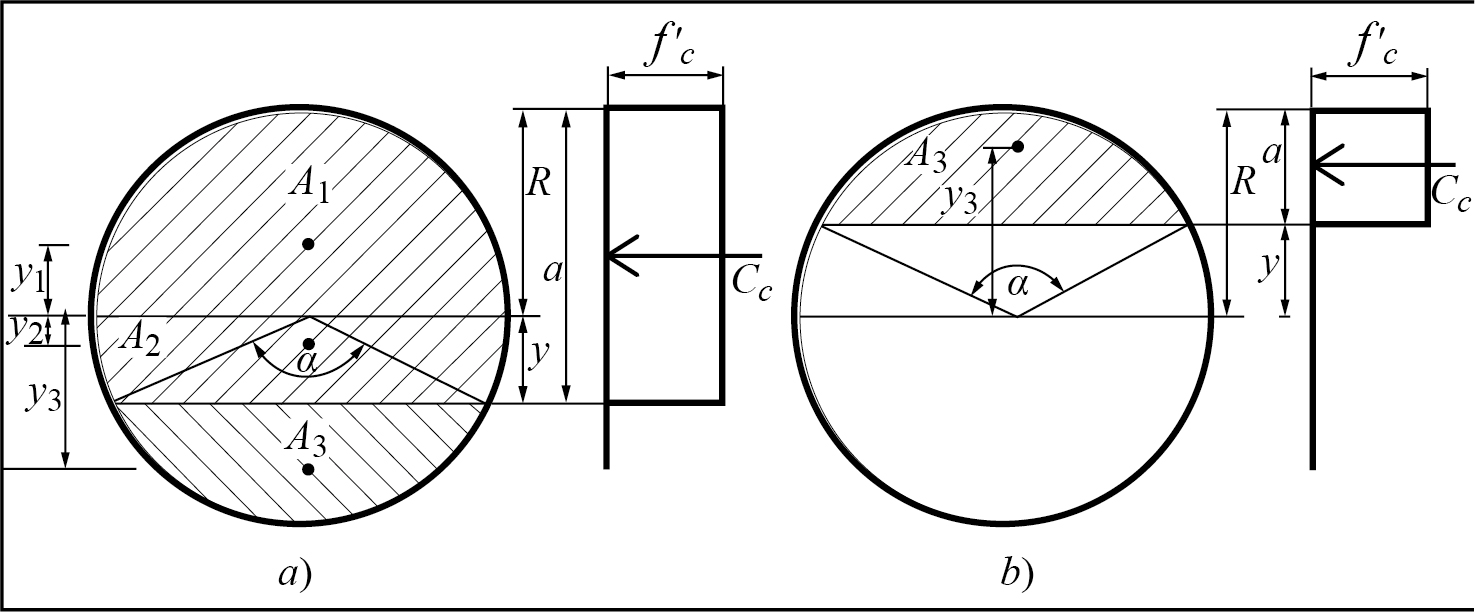
Fuente: elaboración propia. Nota: a) a ≥ R; b) a < R.
Figura 3 Condiciones de la profundidad del bloque de esfuerzos
En la segunda condición, figura 3b, el cálculo se simplifica porque sólo el área A 3 está en compresión. Las ecuaciones 12 y 13 definen la fuerza y momento del concreto.
En otro orden, la deformación εsi y el esfuerzo de la barra i se evalúan con las ecuaciones 14 y 15, donde E es el módulo elástico del acero. La fuerza y momento en las barras se evalúan con las ecuaciones 16 y 17; el segundo término dentro del paréntesis en la ecuación 16 se considera si el acero está en compresión. En ambas ecuaciones n es el número total de barras. Finalmente, las ecuaciones 18 y 19 definen las coordenadas de un punto del diagrama nominal de interacción (Mn , Pn ) para un valor específico de Z. El cálculo de las ecuaciones 1-19 se repiten hasta cuando la variable Z alcance su valor límite. La gráfica 1 muestra un diagrama nominal de interacción.
En la gráfica 1 la capacidad a tensión, Pnt , max es función del área de acero y el esfuerzo de fluencia (ecuación 20). La resistencia máxima en compresión se obtiene sumando la aportación del concreto y acero (ecuación 21).
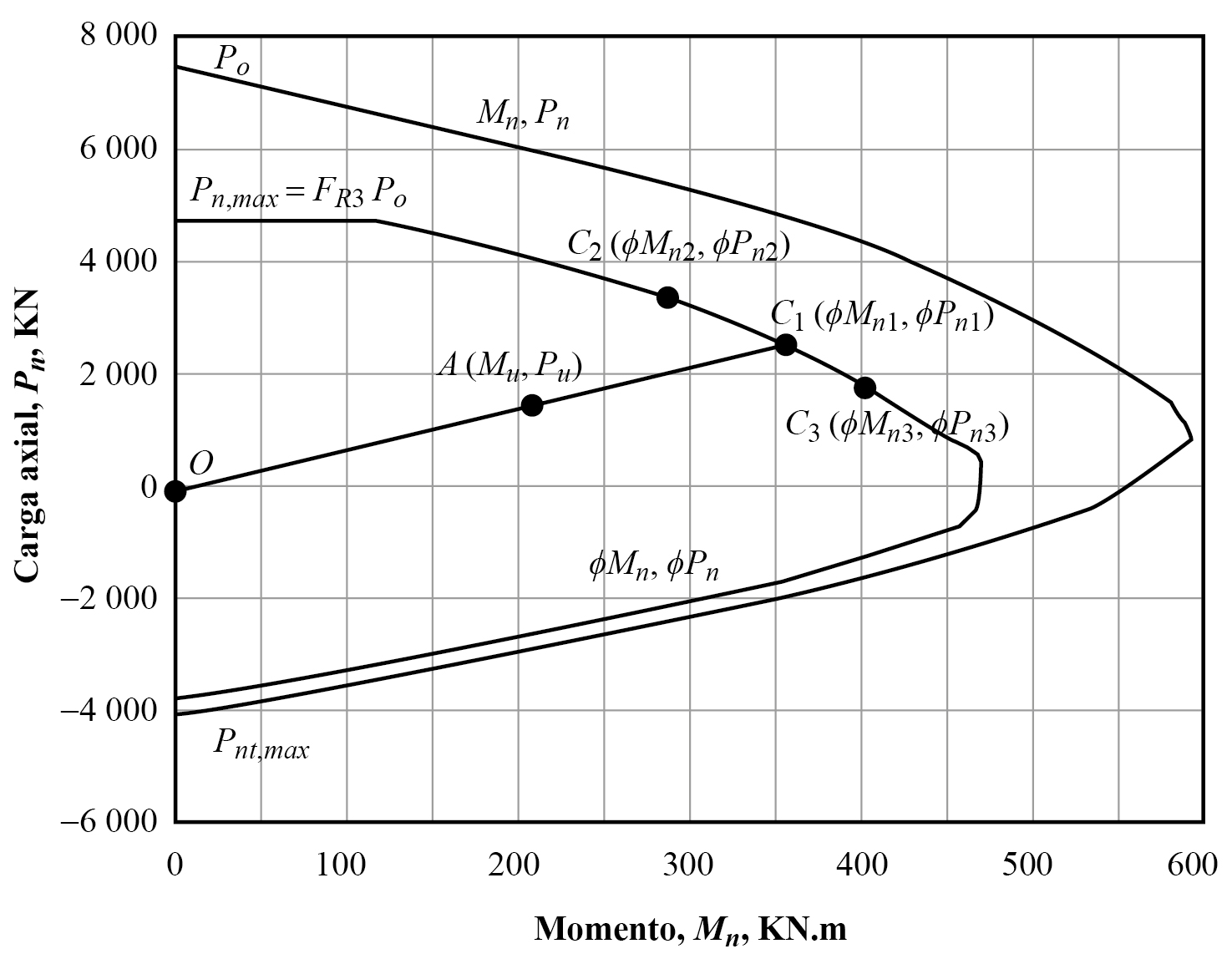
Fuente: elaboración propia.
Gráfica 1 Curva de interacción nominal (Mn - Pn ) y curva resistente (ϕMn , ϕPn )
1. 2. Cálculo del diagrama resistente de interacción
El siguiente paso es calcular el diagrama resistente de interacción multiplicando los valores del diagrama nominal de interacción por los factores de reducción de resistencia (ecuaciones 22 y 23). En este caso, en función de las características del acero transversal, FR 1 toma valores de 0.65 o 0.75, FR 2 vale 0.25 o 0.15. La recta horizontal superior del diagrama en la gráfica 1, se define con la ecuación 23 con FR 3 igual a 0.85 o 0.80.
1. 3. Cálculo de elementos mecánicos resistentes
En el siguiente paso se calcula el momento y carga resistente (ϕMn 1, ϕPn 1) correspondiente al momento y carga últimos (M U , P U ) obtenidos del análisis estructural (gráfica 1). De acuerdo con la gráfica 2, la recta OA inicia en el origen y termina en las coordenadas (MU , PU ) formando un ángulo θ 1 medido en el sentido horario respecto del eje vertical, la intersección de esta recta con la curva resistente define las coordenadas del punto C 1 (ϕMn 1, ϕPn 1). La ubicación se obtiene al comparar el ángulo θ 1 con los ángulos respectivos (θ 2 y θ 3) de las líneas adyacentes OC2 y OC3.
A continuación, se calculan las pendientes de las rectas C2C3 y OA, m 1 y m 2 respectivamente. En el segmento C2C3 se define la ecuación 24 que pasa por las coordenadas (ϕMn 3, ϕPn 3); la ecuación 25 se calcula utilizando la pendiente m 2 de la recta OA (Lehman, 2006).
La solución de este sistema representa las coordenadas del punto C 1 (ϕMn 1, ϕPn 1) (Griffiths y Smith, 2006), que están relacionadas con los elementos mecánicos de diseño (M U, PU ). Por último, se compara la relación M U/ϕMn 1 y PU /ϕPn 1. Si el cociente es menor que 1, el elemento estructural resiste los elementos mecánicos actuantes; en caso contrario deben modificarse las propiedades de la sección o las características de los materiales. El procedimiento descrito fue implementado en el software de código libre Scilab (Scilab, 2021). [1]
1. 4. Aproximación de la aplicación
Con el objetivo de verificar la aproximación de la curva de interacción nominal calculada con la aplicación, los resultados se comparan con dos ejemplos referenciados. En ambos casos, la deformación máxima del concreto es εc = 0.003, la deformación de fluencia del acero es εty = 0.00207 y el esfuerzo de fluencia (fy ) es 414 Mpa (Kent, 2012; Structure Point, 2020).
El primer caso es la columna C1, radio de 25.4 cm y reforzada con 6 barras número 10 (diámetro de 3.22 cm) separadas un ángulo de 60°. La distancia entre ejes de barras y la cara exterior es 6.38 cm. La resistencia a compresión del concreto es (f ׳c) 20.7 MPa (3 ksi) y el acero longitudinal está confinado por espirales del número 3 que cumplen con los requisitos de la norma (figura 4a) (Kent, 2012).
La gráfica 3 presenta dos gráficas: el diagrama nominal referenciado y el diagrama calculado con la aplicación. El error entre ambas en un punto (Mn , Pn ) se calcula con la ecuación 26, donde RR es el módulo del diagrama de referencia y RC es el módulo aquí calculado (cuadro 1). La gráfica 4 muestra la definición de la ecuación 26. El error es negativo cuando la curva calculada con la aplicación envuelve a la curva referenciada y viceversa. El cálculo de las coordenadas de los puntos RC y/o RR se realizó con el procedimiento descrito en el inciso anterior.
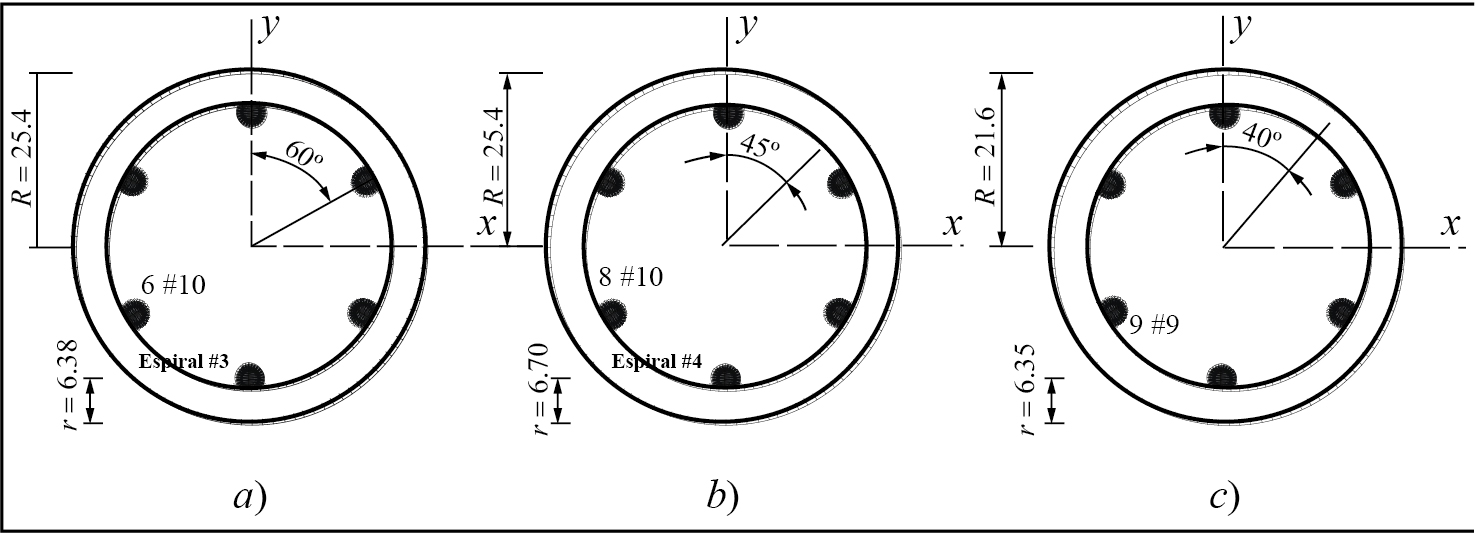
Fuente: elaboración propia. Nota: a) Columna C1 (Kent, 2012), b) Columna C2 (Structure Point, 2020), c) Columna C3 (ACI, 2015). Dimensiones en cms.
Figura 4 Geometría y distribución de acero
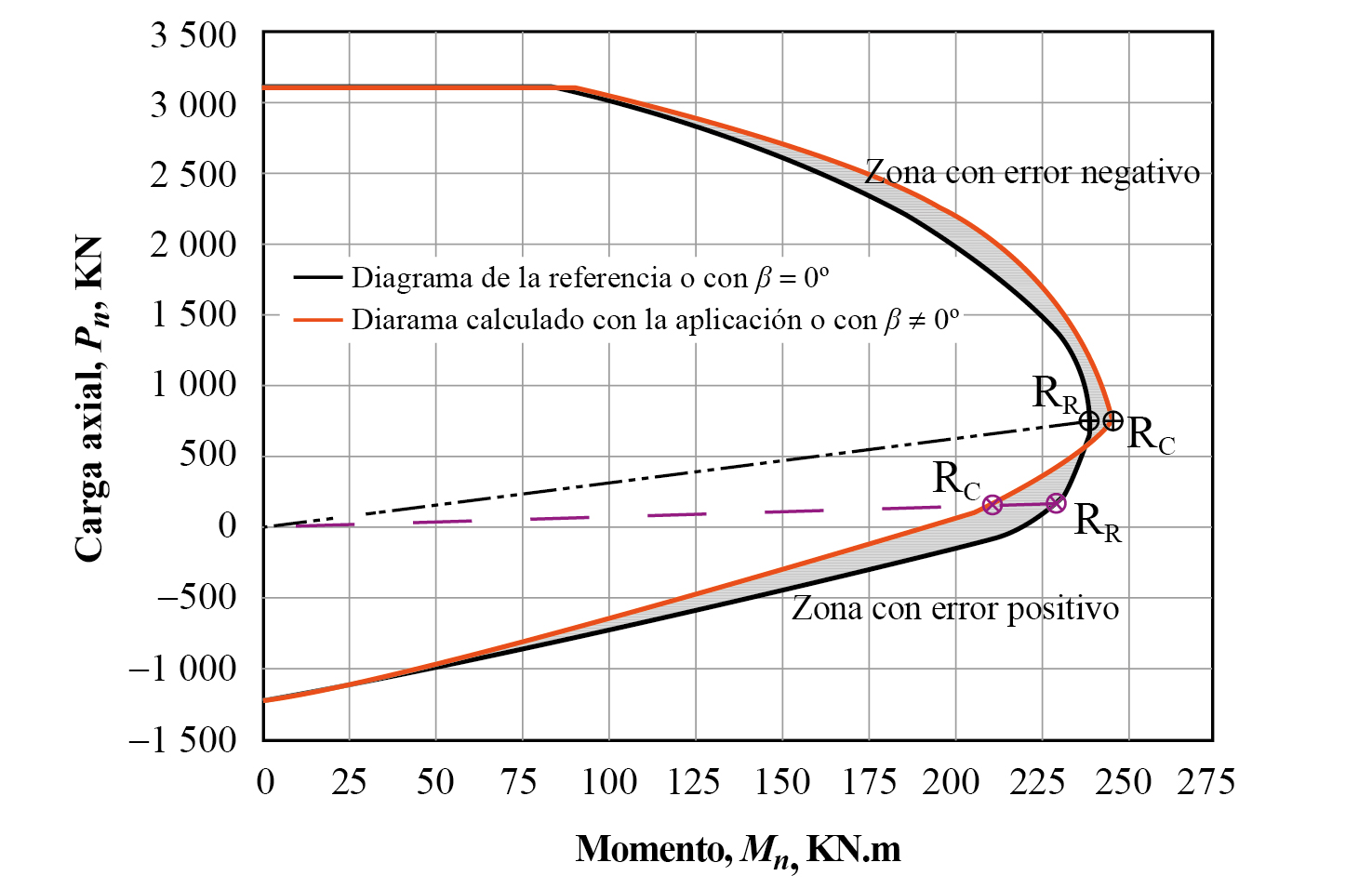
Fuente: elaboración propia.
Gráfica 4 Definición del error y/o variación entre curvas con distinto valor de β
En el segundo caso se analizó una columna con radio de 25.4 cm (C2) y distancia entre el eje de barras y la cara exterior igual a 6.70 cm. El acero longitudinal está formado por 8 barras número 10 (diámetro 3.22 cm) y separadas un ángulo de 45°. La resistencia a compresión del concreto es (f'c) 34.5 MPa (5 ksi); espirales del número 4 confinan el acero longitudinal de acuerdo con los requisitos del ACI (figura 4b) (Structure Point, 2020). La gráfica 5 muestra ambas curvas formadas por siete puntos, como se observa el error máximo es 0.2 % cuando la deformación extrema del acero es est = 0.005 (cuadro 2).
Cuadro 1 Comparación de valores (KN.m)
| a, mm | Condición | Kent, 2012 | Aplicación | Error % | ||
| Mn | Pn | Mn | Pn | |||
| 508.0 | Po | 0.0 | 5 510.0 | 0.0 | 5 514.1 | 0.0 |
| 449.7 | 131.0 | 4 684.0 | 130.9 | 4 683.9 | 0.0 | |
| 428.6 | 160.0 | 4 508.0 | 159.5 | 4 504.1 | 0.0 | |
| 400.9 | 198.0 | 4 219.0 | 198.2 | 4 219.1 | 0.0 | |
| 369.0 | 0.0 fy | 241.0 | 3 844.0 | 240.9 | 3 842.0 | 0.0 |
| 332.9 | 282.0 | 3 396.0 | 282.1 | 3 395.5 | 0.0 | |
| 301.7 | 315.0 | 2 937.0 | 314.6 | 2 936.6 | 0.0 | |
| 270.7 | -0.5 fy | 343.0 | 2 430.0 | 342.6 | 2 430.9 | 0.0 |
| 239.5 | 367.0 | 1 857.0 | 367.2 | 1 858.7 | 0.0 | |
| 223.5 | -1.0 fy | 379.0 | 1 535.0 | 379.2 | 1 533.3 | 0.0 |
| 210.1 | 379.0 | 1 295.0 | 379.0 | 1 294.5 | 0.0 | |
| 196.6 | 378.0 | 1 037.0 | 378.0 | 1 037.7 | 0.0 | |
| 175.1 | 374.0 | 592.0 | 373.5 | 600.3 | 0.0 | |
| 142.7 | 329.0 | 147.0 | 328.8 | 146.6 | 0.1 | |
Fuente: elaboración propia.
Cuadro 2 Comparación de valores (KN.m)
| a, mm | Condición | Structure Point, 2021 | Aplicación | Error, % | ||
| Mn | Pn | Mn | Pn | |||
| 508.0 | Po | 0.0 | 8 462.0 | 0.0 | 8 461.7 | 0.0 |
| 352.3 | 0.0 fy | 308.7 | 5 839.9 | 379.9 | 5 806.2 | -0.1 |
| 262.4 | -0.5 fy | 509.0 | 3 809.5 | 509.3 | 3 781.8 | 0.0 |
| 208.8 | -1.0 fy | 553.1 | 2 308.7 | 552.2 | 2 286.8 | 0.0 |
| 148.5 | es = 0.005 | 448.0 | 167.0 | 448.1 | 172.8 | 0.2 |
| 127.0 | Flexión | 434.2 | 0.0 | 434.0 | 0.0 | 0.1 |
| Pnt,max | 0.0 | -2 712.1 | 0.0 | -2 711.0 | 0.0 | |
Fuente: elaboración propia.
2. Resultados
2. 1. Error en diagramas al considerar la posición del acero de refuerzo
La gráfica 6 y la gráfica 7 representan los diagramas resistentes de interacción de la columna C1 con cuantías de acero entre 2.42 y 4.04%, la resistencia a compresión del concreto es 20.7 MPa (3 ksi) y 34.5 MPa (5 ksi), respectivamente. Cada una contiene cinco series de dos gráficas correspondientes a 6, 7, 8, 9 y 10 barras del número 10. El ángulo entre el eje vertical superior y la primera barra del lado derecho de cada arreglo es la variable β definida en la figura 2; el rango de valores es 30° a 18° corresponde a 6 y diez barra respectivamente. En ambas gráficas la línea continua presenta el caso de β = 0. El cuadro 3 presenta el error máximo (ecuación 26) entre cada par de curvas en función del ángulo β y la excentricidad de la carga. El error es positivo si el módulo del punto de análisis en la curva con β = 0 es mayor al correspondiente de la curva cuando β ≠ 0; en caso contrario, es negativo (gráfica 4). En los cuadros 3 y 4 Exc representa la excentricidad definida por la relación ϕMn /ϕPn .
El mismo procedimiento se realizó en la columna C3 mostrada en la figura 4c (ACI, 2015) con idénticos valores de la resistencia a compresión. Los diagramas resistentes de interacción con β = 0 y β ≠ 0 se muestran en las gráficas 8 y 9. El error máximo se presenta en el cuadro 3.
Adicionalmente, se calcularon las curvas de diseño de las columnas C1 y C3 con valores próximos entre sí de la cuantía de acero longitudinal. La resistencia a compresión fue 20.7 MPa y 34.5 MPa. Tres configuraciones de acero fueron propuestas: 9 #9, 7 #10 y 6 #11. El ángulo β varía entre 30 y 20°. La gráfica 10 y 11 presentan dichas gráficas formadas por dos curvas, donde la primera calculada con β = 0° y en la segunda cuando β ≠ 0. El error máximo en cada caso se muestra en el cuadro 4.
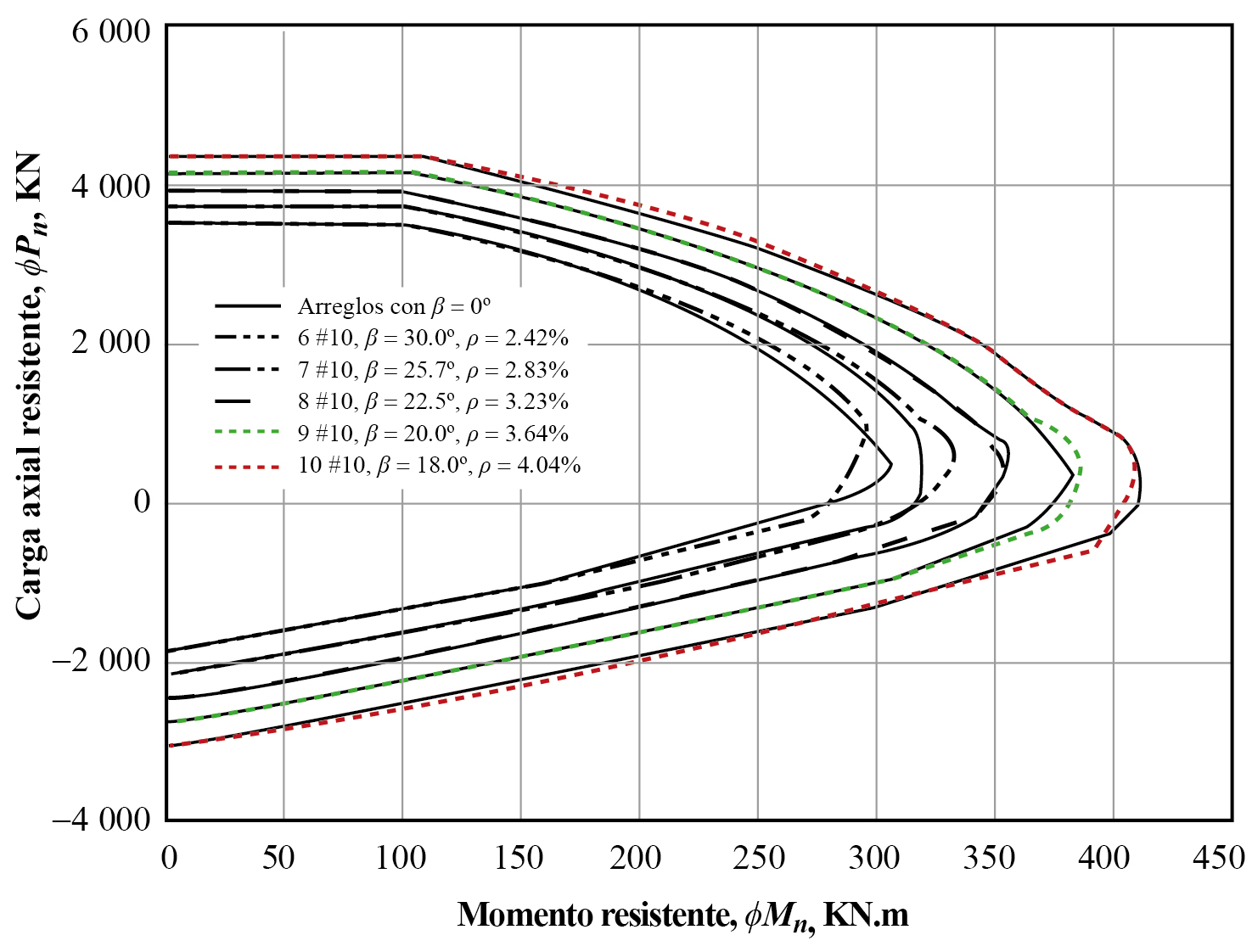
Fuente: elaboración propia. Nota: con ρ variable, resistencia a la compresión f׳c = 20.7 MPa (3 ksi)
Gráfica 6 Diagramas resistentes de interacción de columna C1
El ángulo β y el valor absoluto del error de los cuadros 3 y 4 se presentan en la gráfica 12, donde se muestra una recta envolvente cuya ecuación es ajustada a tres puntos extremos de los datos, por lo que el factor de correlación R es la unidad, los parámetros de la ecuación 27 son A = 0.358 y b = -4.15.
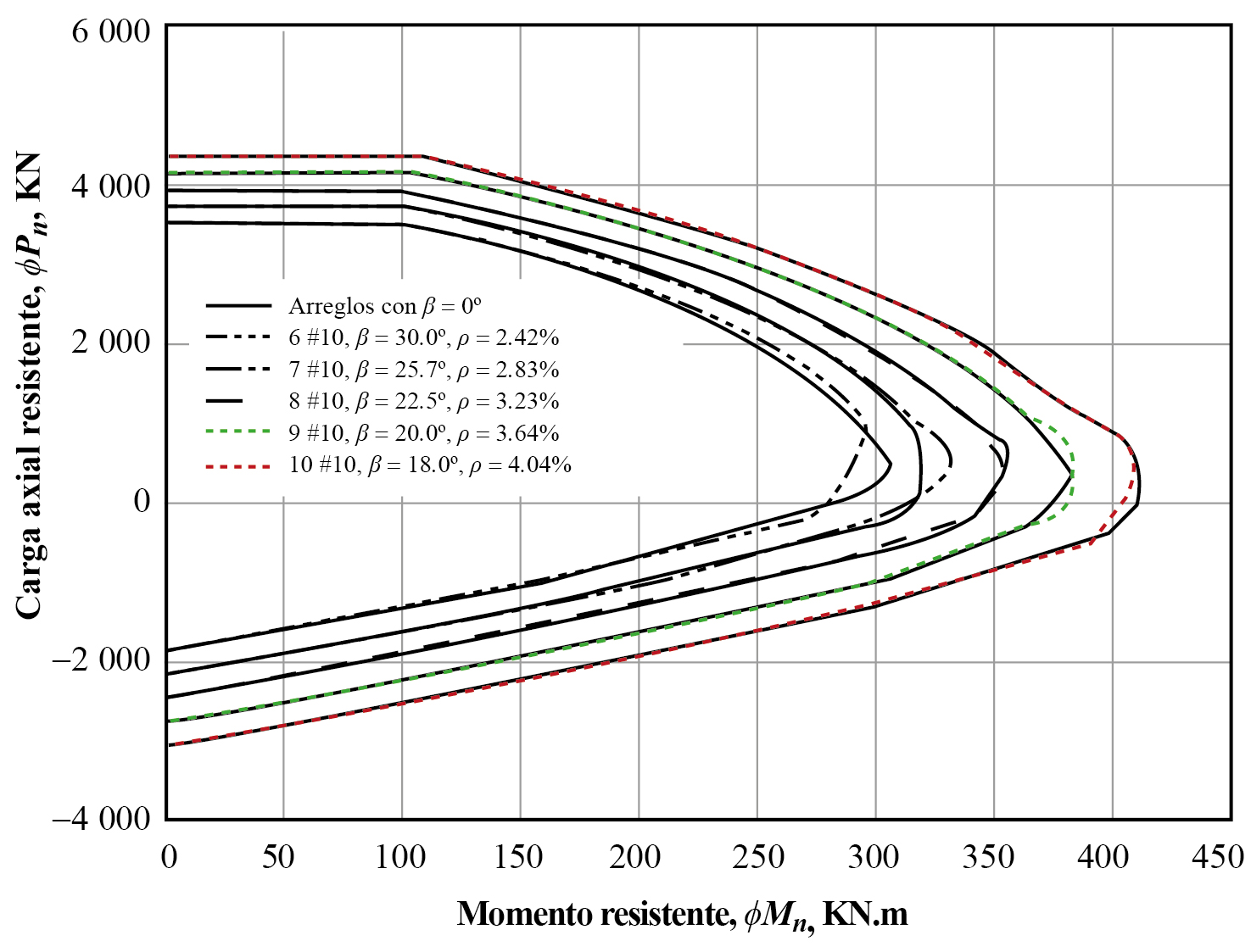
Fuente: elaboración propia. Nota: con ρ variable, resistencia a la compresión f׳c = 34.5 MPa (5 ksi).
Gráfica 7 Diagramas resistentes de interacción de columna C1
Cuadro 3 Error (%) con ρ variable en columnas C1 y C3
| Columna | Acero de refuerzo | Ángulo β en grados | f׳c = 20.7 MPa (3 ksi) | f׳c = 34.5 MPa (5 ksi) | ||
| Exc | Error | Exc | Error | |||
| C1 | 6#10 | 30.0 | 0.65 | 5.7 | 0.44 | 5.8 |
| 6#10 | 30.0 | 0.18 | -1.9 | |||
| 7#10 | 25.7 | 0.54 | -4.4 | 0.38 | -4.2 | |
| 8#10 | 22.5 | 0.53 | 2 | 0.38 | 1.5 | |
| 9#10 | 20.0 | -1.32 | -2.9 | 2.75 | -2.8 | |
| 10#10 | 18.0 | -3.4 | 2.3 | 1.3 | 2.2 | |
| C3 | 6#10 | 30.0 | 0.6 | 5.8 | 0.4 | 5.9 |
| 7#10 | 25.7 | 0.6 | -4.1 | 0.4 | -3.9 | |
| 8#10 | 22.5 | 0.5 | 2.6 | 0.3 | 1.9 | |
| 9#10 | 20.0 | -0.6 | -2.8 | -2.6 | -3.0 | |
| 10#10 | 18.0 | -1.2 | 2.3 | 0.3 | 1.8 | |
Fuente: elaboración propia.
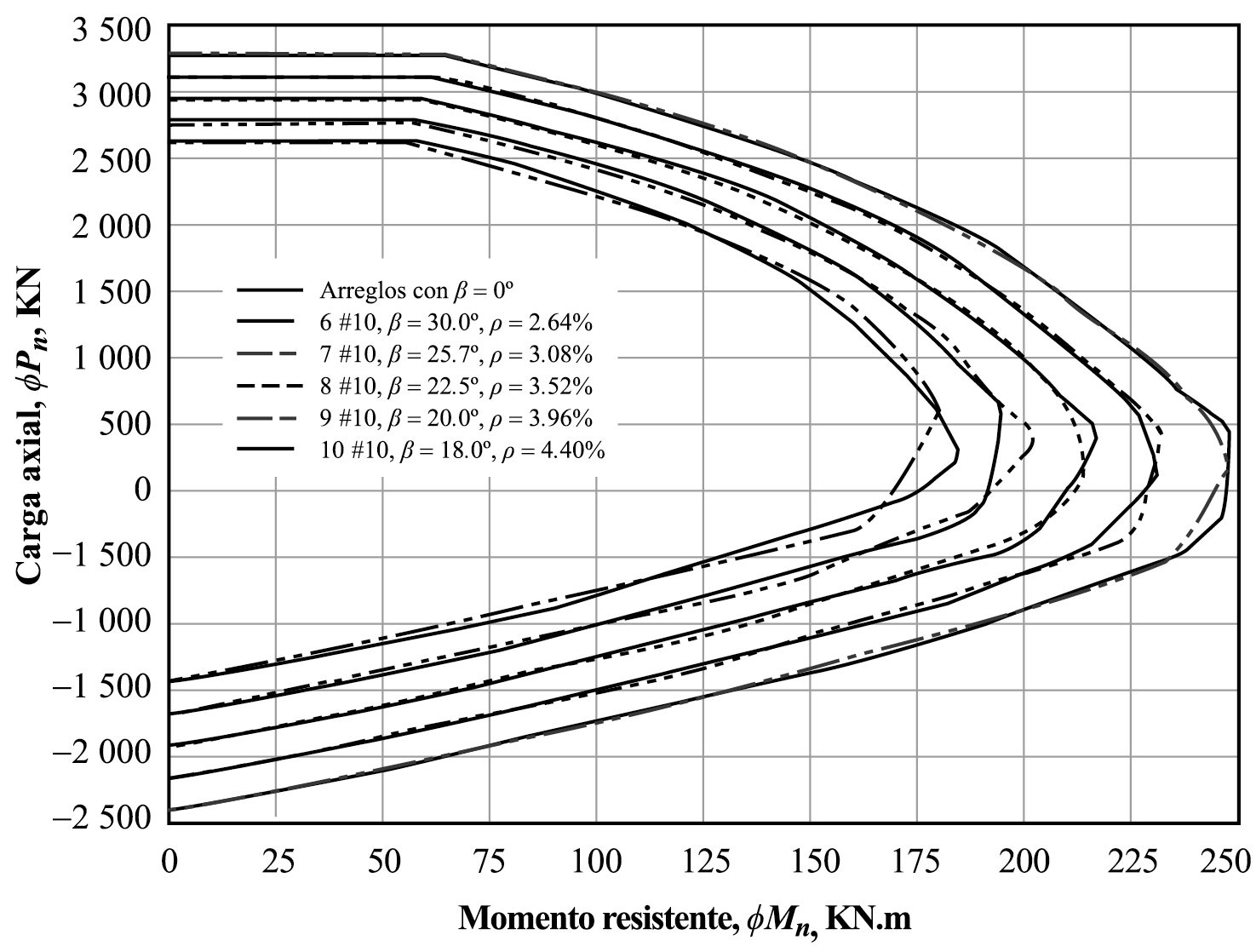
Fuente: elaboración propia. Nota: con ρ variable, resistencia a la compresión f׳c = 20.7 MPa (3 ksi).
Gráfica 8 Diagramas resistentes de interacción de columna C3
2. 2. Diagramas resistentes considerando la posición del acero de refuerzo
Como se observa en el cuadro 3, cuadro 4 y gráfica 6, 7, 8, 9, 10 y 11 hay diferencias en los diagramas de interacción al tomar en cuenta la posición del acero de refuerzo. Si bien en algunos casos el diagrama de interacción con β = 0 envuelve al diagrama con β ≠ 0, en otros la situación se invierte; de esta forma, se desconoce el nivel de seguridad estructural real. Por tal razón, en el diseño deben considerarse las siguientes opciones:
Modificar el valor de la relación MU /ϕMn 1 o PU/ϕP n1, cuyo valor máximo es 1, en función del error relacionado con la cantidad de barras colocadas.
Colocar mayor cantidad de barras distribuyendo el acero requerido.
Construir diagramas de interacción tomando en cuenta la cantidad y posición de las barras de refuerzo.
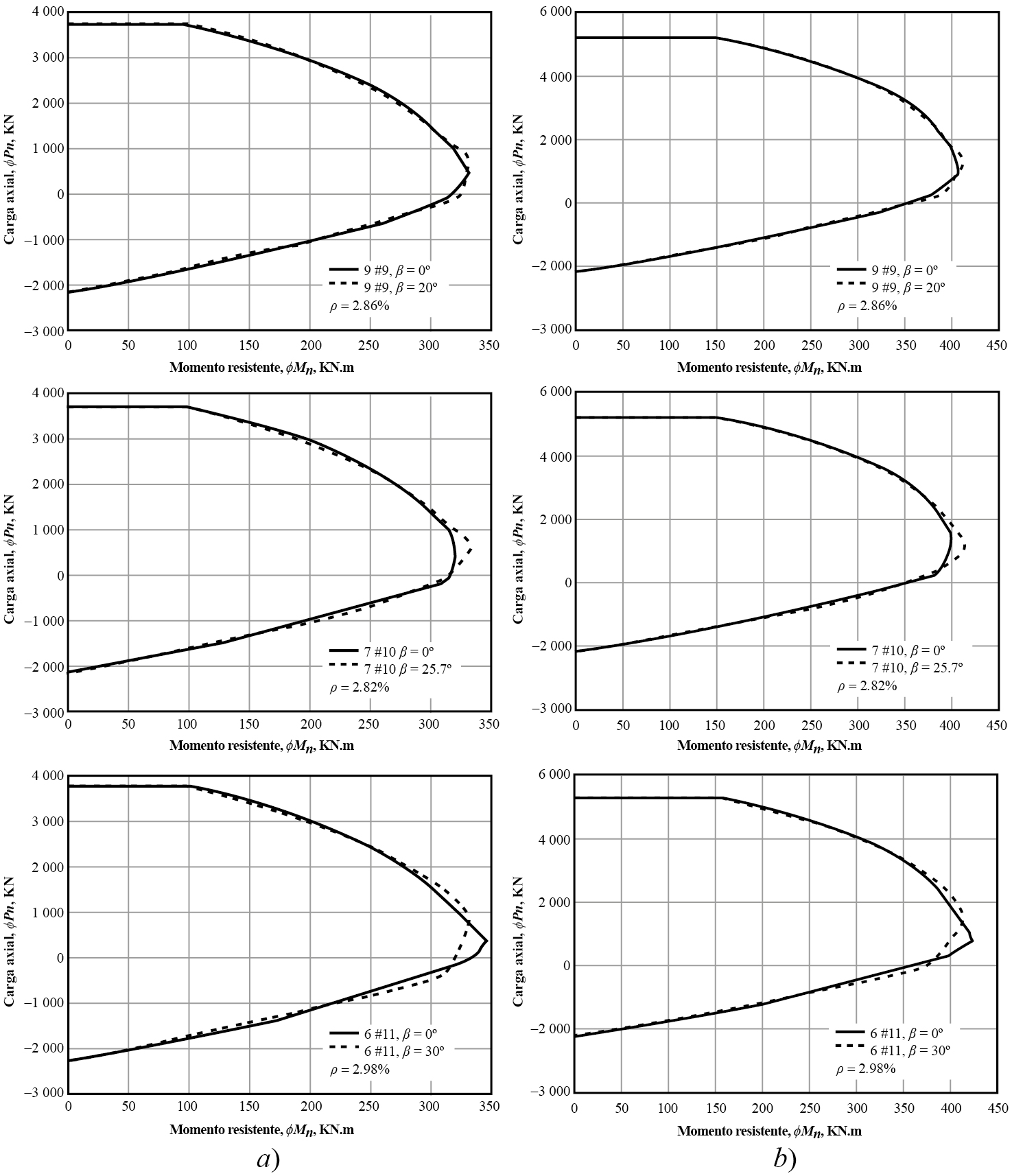
Fuente: elaboración propia.
Gráfica 10 Diagramas resistentes de interacción en columna C1 con ρ constante y diferente valor de resistencia a la compresión: a) f׳c = 20.7 MPa (3 ksi), b) f׳c = 34.5 MPa (5 ksi)
Cuadro 4 Error (%) con ρ constante en columnas C1 y C3
| Columna | Acero de refuerzo | Ángulo β | f׳c = 20.7 Mpa (3 ksi) | f׳c = 34.5 Mpa (5 ksi) | ||
| Exc | Error | Exc | Error | |||
| C1 | 9#9 | 20.0 | -5.0 | -2.8 | 1.3 | -2.9 |
| 7#10 | 25.7 | 0.5 | -4.0 | 0.4 | -4.2 | |
| 6#11 | 30.0 | 0.9 | 5.8 | 0.5 | 6.0 | |
| C3 | 9#9 | 20.0 | -0.7 | -2.9 | -3.6 | -3.0 |
| 7#10 | 25.7 | 0.9 | -4.2 | 0.5 | -4.1 | |
| 6#11 | 30.0 | 68.0 | 6.3 | 0.8 | 6.6 | |
Fuente: elaboración propia. Nota: Exc es la excentricidad igual a φMn / ϕPn .
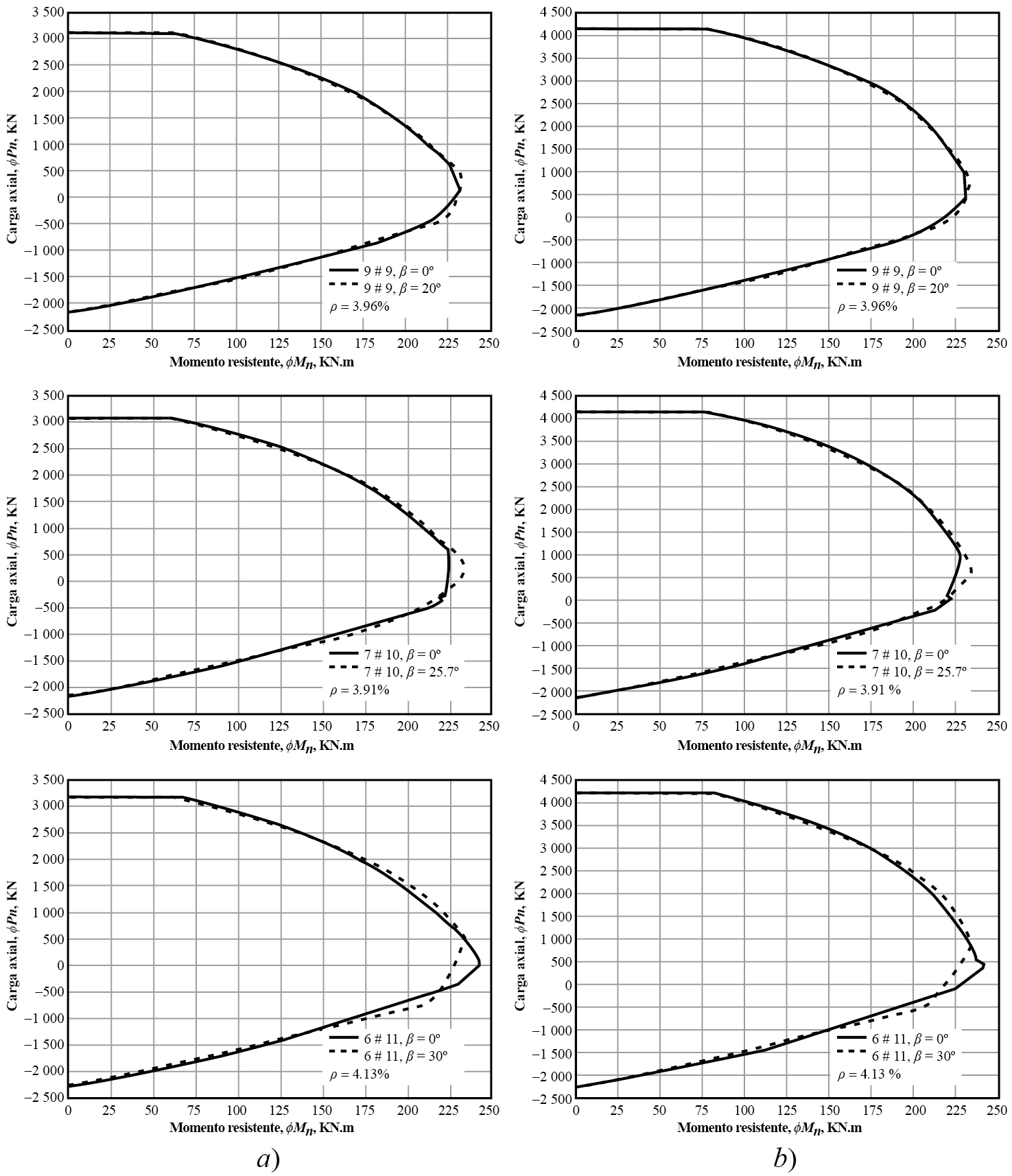
Fuente: elaboración propia. Nota: con ρ constante y diferente valor de resistencia a compresión: a) f׳c = 20.7 MPa (3 ksi), b) f׳c = 34.5 MPa (5 ksi).
Gráfica 11 Diagramas resistentes de interacción en columna C3
Con la idea expresada en el último punto y utilizando la aplicación, se elaboraron los diagramas resistentes de interacción mostrados en la gráfica 13 y 14. De acuerdo con la norma, en columnas confinadas por espirales deben colocarse al menos 6 barras. La gráfica 13 presenta el diagrama resistente correspondiente para este caso. En forma similar a las referencias (ACI, 2015) se denominó C24.5-421.80-1.00-6, donde la variable C define una columna circular, el valor 24.5 es la resistencia a compresión del concreto en MPa, el parámetro 421 es el esfuerzo de fluencia del acero en Mpa y la relación distancia entre ejes de barras respecto al diámetro de la columna es la variable γ, igual a 0.80. El diámetro de la columna es la variable D en metros, igual a 1.00, donde el último dígito representa la cantidad de barras, que es 6 en este caso.
En el segundo diagrama, gráfica 14, cambia tanto la resistencia a compresión del concreto (39.2 MPa) como la cantidad de barras longitudinales, 8 barras. Los valores del ángulo β son 30° y 22.5° en la gráfica 13 y en la gráfica 14, respectivamente.
En los diagramas de la gráfica 13 se utilizaron barras del número 5, 6, 7, 8 y 10; así, la cuantía de acero está entre 1.52 %-6.05%. En los diagramas de la gráfica 14 se utilizaron barras del número 4, 6, 7, 8 y 10. Los límites de la cuantía de acero son 1.29% y 8.00 %. En ambos casos este parámetro se encuentra en el intervalo permitido (1%-8%),
Las espirales confinantes cumplen con los requisitos normativos, por lo que los factores de reducción de resistencia utilizados en las ecuaciones 22 y 23 son FR 1 = 0.75, FR 2 = 0.25 y FR 3 = 0.85. En los diagramas también se dibujaron rectas para distintos valores de e/D, donde e es la excentricidad de la carga y D representa el diámetro de la columna.
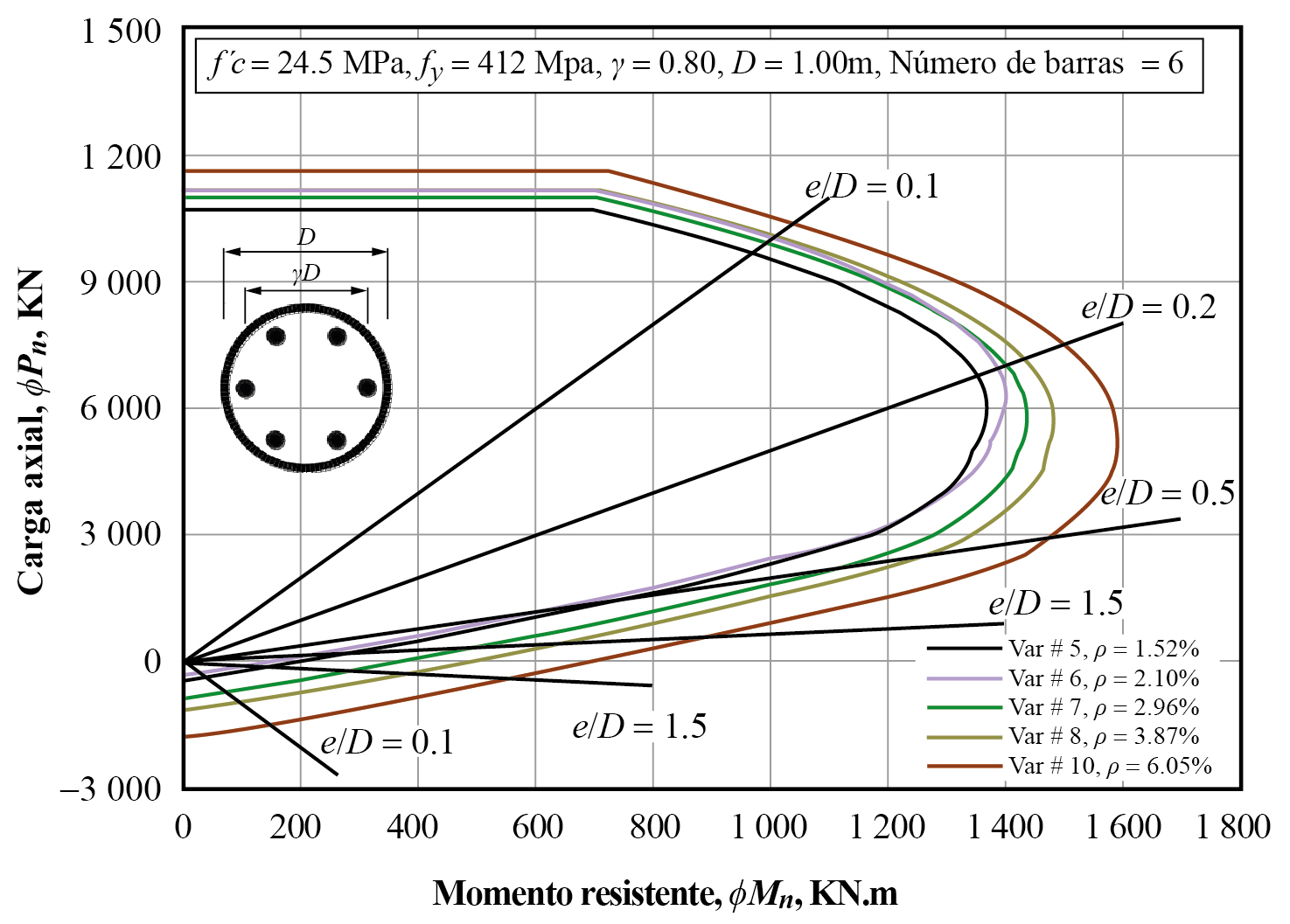
Fuente: elaboración propia.
Gráfica 13 Diagrama resistente de interacción con 6 barras de refuerzoDiagrama de interacción c24.5-412.80-1.00-6
Prospectiva
La mayoría de los diagramas de interacción para diseño de columnas cortas de forma circular sólidas, normalmente adimensionales, no consideran la posición del acero vertical, ya que éste se modela como un anillo continuo –también las referencias son pocas– y sólo Wight y Macgregor (2012) expresan que el error es despreciable cuando las columnas tienen al menos 8 barrasFinalizar. Para este caso, los resultados indican un error de 4%.
Como se observa, en la cercanía de la falla balanceada, existe la posibilidad de subestimar o sobreestimar la capacidad de las columnas. De acuerdo con la ecuación 26, gráfica 4 y cuadros 3 y 4, un error negativo sobrestima la capacidad de la columna armada con 7 barras en hasta 4%. Un error adicional se puede generar cuando en proyecto no se indique la colocación exacta del acero de refuerzo en la sección circular o en obra no se respete esta indicación y, como consecuencia, la envolvente de capacidad en la zona con error positivo de la gráfica 4 podría ser el diagrama calculado con β ≠ 0 y generar un error de hasta 7% si se colocan 6 barras.
Por otro lado, el proceso de análisis y diseño estructural tiene bases probabilistas al considerar valores mayores a uno en los factores de carga y menores a 1 en los factores de reducción de resistencia. Sin embargo, cuando se diseña o revisa una columna sometida a flexocompresión se considera un criterio determinista estricto de la relación MU /ϕMn 1 o PU /ϕPn 1, la cual por seguridad y con la idea de optimizar al máximo la capacidad de las columnas, principalmente las ubicadas en zonas de alto peligro sísmico, debe ser igual a la unidad. Este es otro punto a favor para utilizar los diagramas de interacción “reales”, es decir, considerando la posición del acero de refuerzo como los mostrados en las gráficas 13 y 14. Finalmente, considerando un error igual al 2%, y despejando el ángulo β de la ecuación 27, se requiere colocar 10 barras de refuerzo en la sección. También es necesario continuar con la investigación, ya que existen pocas referencias y escasas aplicaciones, comerciales o académicas, sobre el tema. Además, debe analizarse el impacto en el comportamiento global no lineal de una estructura con este tipo de columnas.
Conclusiones
El extenso uso de columnas circulares sólidas en zonas de alto riesgo sísmico obliga a desarrollar diagramas de interacción que optimicen la capacidad a flexocompresión de dichos elementos. Bajo esta idea se desarrolló un algoritmo de acceso libre que evalúa el diagrama de interacción considerando la ubicación del acero de refuerzo vertical. Para comprobar la exactitud, los diagramas obtenidos fueron comparados con dos ejemplos de diagramas referenciados. Los resultados son aceptables y el error no excede 0.2 %.
A continuación, se evaluaron los diagramas resistentes de interacción de dos columnas con dos valores de resistencia a compresión: 20.7 MPa (3 ksi) y 34.5 MPa (5 ksi) y dos posiciones del acero de refuerzo: a) la primera barra coincide con el eje vertical, b) la primera barra se desplaza hacia la derecha la mitad del ángulo existente entre barras. En un primer análisis (20 pares de diagramas de interacción) se varía y en un segundo (12 pares de gráficas) se mantuvo constante la cuantía de acero vertical, pero siempre cambiando la cantidad de barras. El parámetro de control (ángulo β) está entre 18°-30° y el error varía de -4.2% a 6.6% cuando se utilizan entre 6 y 10 barras de refuerzo.
Los resultados definen una relación lineal entre la cantidad de barras y el error entre dos diagramas resistentes de interacción (β = 0 y β ≠ 0). El error se reduce al 2% cuando se colocan al menos 10 barras de refuerzo. En caso de utilizar una cantidad menor, entre 6 y 9 barras, deben calcularse diagramas similares a los aquí presentados utilizando la aplicación Open Source desarrollada ex profeso. En este caso es importante definir la correcta colocación del acero logitudinal y garantizar su cumplimiento en obra para que la flexión durante la vida útil del elemento ocurra respecto al eje neutro de diseño.











 nueva página del texto (beta)
nueva página del texto (beta)










