1. Introducción
Actualmente, es bien conocido que el mundo requiere más que nunca energía limpia, además de medios eficientes para manejarla, existen múltiples estrategias para producirla desde métodos clásicos como sistemas aerogeneradores [1], sistemas fotovoltaicos [2], incluso sistemas hidroeléctricos que nos brindan energía a gran escala [3]. Sin embargo, en las últimas décadas se ha buscado obtener o encontrar formas de recolectar energía a pequeña escala [4-10]. Con el avance y desarrollo de la electrónica se han creado sistemas más eficientes, es decir, sistemas que ahorran y aprovechan la energía de una mejor forma, llegando a la construcción de sistemas de ultra-bajo consumo [11-12]. Se sabe que la energía encontrada en el ambiente puede ser recolectada, bajo este principio se han desarrollado las estrategias antes mencionadas, de igual forma ha habido un avance significativo en el desarrollo de materiales que transforman otros tipos de energía en energía eléctrica, desde materiales termoeléctricos, piroeléctricos, triboeléctricos, piezoeléctricos, entre otros. En este sentido, el estudio de nuevas formas de generación de energía se encuentra apoyándose de sistemas de simulación como COMSOL MultiphysicsⓇ que permiten modelar los materiales, los ambientes y las condiciones que propician la conversión energética, es decir, la física que rige el comportamiento de estos materiales, donde es posible modelar materiales generadores de energía y su eficiencia en ambientes y condiciones específicas. El uso de este tipo de programas se ve reflejado en múltiples estudios [13-17] donde se plantea el diseño de estos dispositivos y su evaluación teórica, para su posterior fabricación.
En este trabajo se plantea proyectar la forma y las consideraciones que deben tenerse en cuenta para generar una simulación válida para sistemas generadores de energía termoeléctrica (TEG). Los parámetros que se evaluarán serán la eficiencia energética considerando diferentes gradientes de temperatura (ΔT) de acuerdo a la temperatura corporal normal de 37 ºC, en dos estructuras TEG convencionales con un área de 1 cm2: un TEG con termopares a escala milimétrica y otro con termopares a escala micrométrica, con una forma estructural y escala definida para su posible fabricación y uso en sistemas portables.
El principal objetivo es poder ver las implicaciones en la generación de energía, comparar y consolidar el conocimiento que se tiene de estos dispositivos con otras investigaciones, además de desarrollar la descripción metódica de la simulación de los sistemas generadores de energía del tipo TEG.
2. Estado del arte
La generación de energía eléctrica por medio de la diferencia de calor entre los materiales semiconductores de un TEG, es una herramienta en constante desarrollo donde podemos encontrar diversos tipos de diseños estructurales. Los termogeneradores utilizados para sistemas biológicos, en específico, aquellos que utilizan la temperatura corporal como fuente de calor, han sido estudiados y probados por diversos autores que demuestran su uso y factibilidad, al evaluar su portabilidad y eficiencia energética [18-21]. En [22] simularon y fabricaron un termogenerador de telururo de bismuto portable, utilizado en la palma de la mano del cuerpo humano, evaluaron diversos parámetros que podrían influir directamente en la generación de energía, probando que los termogeneradores pueden ser aplicados en partes estratégicas del cuerpo humano para una máxima generación de energía eléctrica. En [23] simularon un termogenerador en forma de anillo con distintos materiales como el Bi2Te3, seleniurio de bismuto (Bi2Se3) y teleruro de antimonio (Sb2Te3), mostrando que el Bi2Te3, es de los materiales que muestran mejores resultados en la generación de energía. El diseño de estructuras de este tipo de materiales es clave en este campo de investigación. En [24], evaluaron y compararon la longitud y espesor de las aletas del material Bi2Te3, integrado en el diseño del TEG, obteniendo como resultado una mayor eficiencia energética, cuando se aumenta la longitud de las piernas dentro de la estructura. Los materiales tipo-N y tipo-P en la integración de los TEG son una parte fundamental del funcionamiento, por lo que la modificación de la estructura de estos influye en la eficiencia energética, tal y como describen en [25], donde el análisis demostró que la distribución de los materiales influye en la dispersión del calor, así como otros parámetros en los TEG son afectados por el tipo de estructura implementada.
2.1 Funcionamiento de un generador termoeléctrico (TEG)
La generación de energía termoeléctrica es descrita por el fenómeno Seebeck el cual se describe como una fuerza electromotora que se genera a lo largo de un dominio conductor cuando existe un gradiente de temperatura, produciendo un voltaje eléctrico [26].
Más en específico, de acuerdo a la figura 1, al existir un gradiente de temperatura (ΔT) a través de un termopar conformado por materiales semiconductores tipo-N y tipo-P conectados en serie por un conductor eléctrico, y confinados entre dos placas térmicas que funcionan como aislante eléctrico, donde a la placa superior es expuesta a una fuente de calor (TC), y la inferior a una fuente frio (TF), ocurre el movimiento de electrones de un extremo a otro a lo largo de las columnas tipo-N y tipo-P, específicamente, del extremo caliente al extremo frío [26]. Este efecto crea electrodos positivos y negativos que generan una diferencia de potencial (ΔV), que produce una potencia eléctrica (P) proporcional al flujo de corriente (I), generado por la resistencia de carga (RL).
El valor de la potencia eléctrica suministrada en (RL) está dada por la ecuación (1),
Considerando la contribución de los materiales, contactos, electrodos y cables, además de la resistencia interna del módulo TEG (RΩ), la corriente se determina con la ecuación (2)
que al sustituirse en la ec. (1), la potencia eléctrica se convierte en la ecuación (3),
donde, N, es el número de termopares que conforman al módulo TEG, S, es el
coeficiente de Seebeck, y el parámetro
La eficiencia de conversión (η) de un TEG se presenta en la ecuación (4) y se define como la razón entre la P y el calor absorbido sobre la fuente de calor (QC), definido como en la ecuación (5),
donde, K, es la conductividad termal.
Sustituyendo la ecuación (3) y
ecuación (5) en la ecuación (4) y diferenciando η con
respecto a la razón
donde, ZT, es la figura de mérito adimensional [8].
3. Metodología, simulación numérica de un TEG
La figura 2 presenta el modelo CAD de un termopar de columnas de Bi2Te3, una tipo-N y una tipo-P conectadas eléctricamente en serie, por un electrodo de cobre y térmicamente en paralelo, por placas de tungsteno que funcionan como aislante eléctrico.
Para la simulación se diseñaron dos estructuras TEG de 1 cm² conformadas por un número n de termopares de acuerdo al área transversal de las columnas, para el primer TEG de 1 mm², y para el segundo TEG de 250 μm². La figura 3 presenta los parámetros físicos descritos a detalle en la Tabla 1 para el TEG (mm) y el TEG (μm).
Tabla 1 Características de las estructuras simuladas.
| Variable | TEG (mm) | TEG (μm) |
|---|---|---|
| Altura del TEG (HTEG) | 2.5 mm | 500 μm |
| Ancho y espesor del TEG (WTEG,LTEG) | 1 cm | 1 cm |
| Área transversal de una columna del termopar (Wc) | 1 mm2 | 250 μm² |
| Distancia entre columnas (dc) | 0.5 mm | 200 μm |
| Altura del electrodo (Helectrodo) | 100 µm | 30 μm |
| altura del cerámico (Hcerámico) | 0.3 mm | 100 μm |
Las propiedades de los materiales termoeléctricos se definieron desde la librería de COMSOL MultiphysicsⓇ, los cuales se presentan en la tabla 2.
Tabla 2 Propiedades de los materiales.
| Parámetro | Bi2Te3 tipo-N | Bi2Te3 tipo-P | Cobre | Tungsteno |
|---|---|---|---|---|
| Capacidad de calor (J/(Kg•K)) | 154 | 154 | 385 | 132 |
| Densidad (Kg/m3) | 7700 | 7700 | 8960 | 17800 |
| conductividad térmica (W/(m•K)) | k(T) | k(T) | 400 | 175 |
| Conductividad eléctrica (S/m) | σ(T) | σ(T) | 5.998x107 | - |
| coeficiente de Seebeck (V/K) | S(T) | -S(T) | 6.5x10-6 | - |
| permitividad relativa | 1 | 1 | 1 | - |
3.1 Ecuaciones de gobierno
El efecto termoeléctrico es la conversión directa de diferencias térmicas a voltaje eléctrico o viceversa. En COMSOL MultiphysicsⓇ, la interfase de efecto termoeléctrico, combina las interfaces de transferencia de calor en sólidos (ht) y corrientes eléctricas (ec) para modelar los efectos Peltier-Seebeck-Thomson.
En específico, de acuerdo al diagrama de la figura 4, las características térmicas se obtienen por medio del módulo ht donde se define una diferencia de temperaturas, que genera una corriente eléctrica aislada definida por el módulo “ec” cuyo valor se determina por un circuito eléctrico de acondicionamiento [28, 29].
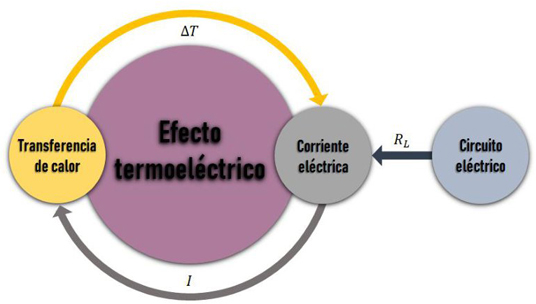
Figura 4 Diagrama de bloques del modelo físico de COMSOL Multiphysics® para la simulación del efecto termoeléctrico.
Este efecto se encuentra gobernado por la forma diferencial de la ecuación de transferencia de calor y, la densidad de corriente continua.
La ecuación de transferencia de calor se utiliza para modelar el balance de energía en un sólido el cual se origina de las contribuciones de conducción, convección, y radiación, la cual se define como en ecuación (7),
donde, ρ es la densidad, Cp es la capacidad de calor, q es el vector flujo de calor y Q es la fuente de calor de Joule.
Para manejar las corrientes en el medio conductivo en un material isotrópico, la ecuación de continuidad (8),
donde, J, es el vector de la densidad de corriente eléctrica establecida.
El fenómeno termoeléctrico es acoplado mediante la contribución del efecto Seebeck definido en la ecuación (9),
donde, σ, es la conductividad eléctrica.
El vector de densidad del flujo de calor, q, definido por la ley de Fourier, se modifica de acuerdo a la contribución PJ de la forma en ecuación (10),
donde, el primer término representa la conducción de calor en la estructura, mientras que el segundo término representa la relación lineal entre el campo eléctrico y el gradiente de temperatura debido a la contribución de una corriente externa definida por el efecto Seebeck que modifica el vector de la densidad de corriente, J, definido por la ley de Ohm, de la forma en la ecuación (11),
donde, k es la conductividad termal, P es el coeficiente de Peltier, y E es el campo eléctrico descrito por la función potencial de la ecuación (12).
Sustituyendo la ec. (10) y ec. (11) en ec. (7) y ec. (8) se produce el sistema de ecuaciones parciales acopladas que describen fenómeno termoeléctrico en un sistema isotrópico conformado por la ecuación (13) y (14).
Como consecuencia se genera un gradiente de voltaje a lo largo de cada uno de los elementos termoeléctricos cuya intensidad se relaciona con la potencia de consumo de la fuente de calor superficial de Joule de acuerdo al campo eléctrico de Seebeck en la ecuación (15).
Las ec. (7), ec. (8), y el sistema de ecuaciones formado por la ec. (13) y ec. (14), constituyen la formulación fuerte que representa las condiciones de frontera iniciales del sistema. Cuando las condiciones iniciales son definidas de manera precisa, COMSOL MultiphysicsⓇ emplea el Método de Elementos Finitos (FEM) para analizar la distribución de temperatura, voltaje y flujos en el dominio (Ω) definido por un número n de elementos finitos [30]. Mediante la formulación débil de Galerkin [31], el sistema de ecuaciones parciales se transforma a un sistema de ecuaciones integrales que plantea funciones base aplicadas en cada uno de los elementos para encontrar la aproximación a la solución numérica mediante la resolución de un sistema lineal representado de forma general en la ec. (16),
donde, las submatrices KT, KTE y KE, llevan a la solución de temperaturas y potenciales eléctricos en la forma de flujo de calor y corrientes eléctricas, respectivamente.
3.2 Condiciones de frontera
Las condiciones de frontera se definieron de acuerdo a la figura 5. Para el módulo “ht”, la superficie de la placa superior de tungsteno fue definida como la fuente de calor (TC), donde la temperatura se mantuvo constante de acuerdo al valor de la temperatura superficial de la piel T0 = 310.15 ºK. La superficie de la placa inferior se definió como la superficie fría (TF) con un valor calculado de acuerdo a ΔT. El resto de las superficies se definieron como superficies aislantes de calor. Para el módulo “ec” las columnas de Bi2Te3 tipo-N y tipo-P se conectaron en serie mediante los electrodos de cobre. La superficie inferior de los electrodos conectados a los extremos de las columnas se definió con un potencial V=0 donde el electrodo de la columna tipo-P se conectó a tierra, mientras que el tipo n se conectó a una terminal, ambos unidos por un circuito eléctrico “ec” de acondicionamiento con una resistencia RL. El resto de las superficies eléctricas se definieron como superficies aislantes de electricidad.
3.4 Mallado
Debido a que cada uno de los elementos que conforman a los TEG diseñados cuentan con secciones transversales constantes, para cada uno de ellos se generó un mallado cuadrangular. En específico, las superficies de los electrodos que conectan las columnas se definieron como superficies de origen para las cuales se generó una malla tipo mapeo, mientras que las superficies de las placas de tungsteno que conectan a los electrodos se definieron como superficies definidas con una malla tipo cuadrangular libre. Finalmente, para cada dominio se generó una malla tipo swept.
3.5 Estudio de COMSOL
Para el modelado del efecto termoeléctrico, se definió un estudio estacionario paramétrico con el cual se evaluó la generación de energía termoeléctrica de acuerdo a una diferencia de temperatura ΔT con una resistencia de carga variable RL. La tabla 3 presenta los valores evaluados para cada uno de los modelos diseñados.
4. Resultados
4.1 Termogenerador eléctrico a escala milimétrica (TEG mm)
Dentro del procedimiento descrito en la metodología está la simulación, revisión y análisis de dos estructuras TEG, una en escala milimétrica y otra a escala micrométrica. En la figura 6 se presenta el TEG (mm) diseñado de acuerdo a los parámetros definidos en la tabla 1. En la figura 6 (a) se observa la cantidad de 18 termopares encontrados en el área definida de 1 cm² conformada por un total de 18 columnas de Bi2Te3 tipo-N y 18 de Bi2Te3 tipo-P intercaladas entre sí y conectadas eléctricamente en serie por los electrodos de cobre y térmicamente en paralelo por las placas de tungsteno. Además, en la figura 6 se definen las condiciones de frontera de acuerdo a la descripción de la figura 5.
La dispersión de temperatura y potencial eléctrico a través de la estructura del TEG (mm) para un ΔT de 15 ºK, se presentan en la figura 7.
Las gráficas de la figura 8 presentan la relación entre el valor de la y la potencia y el voltaje generado en el módulo TEG (mm) de acuerdo a los 3 valores de ΔT analizados, en azul, ΔT = 5 ºK, en verde, ΔT = 10 ºK, y en rojo, ΔT = 15 ºK. En la Figura 8(a) se observa la potencia en función a la RL con una potencia máxima generada para una RL = 0.71 Ω. En la Figura 8(b) podemos determinar el valor del voltaje de operación óptimo producido en función del valor de la RL relacionado con la potencia máxima generada para cada ΔT analizado.
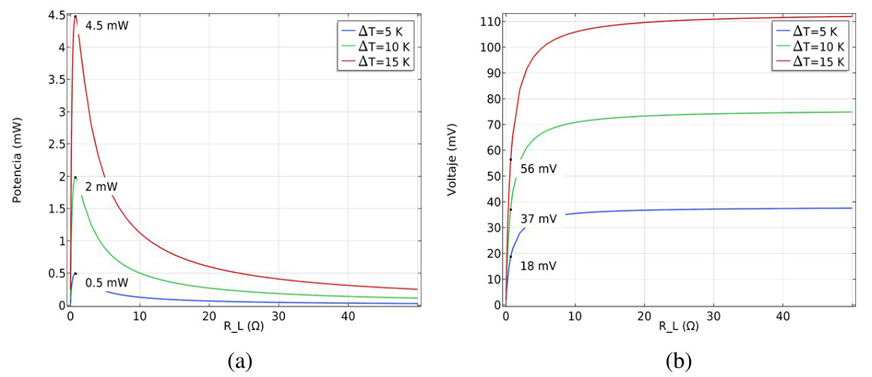
Figura 8 Gráficas para el TEG (mm) en función a la resistencia de carga. En (a) potencia vs. resistencia de carga y (b) voltaje vs. resistencia de carga.
De la misma manera podemos caracterizar el funcionamiento del TEG (mm) de acuerdo a la corriente óptima para determinar la potencia máxima generada. En la figura 9 se presentan los gráficos del voltaje y la potencia en función de la corriente. Para cada uno de los gradientes de temperatura, ΔT, analizados, en la figura 9(a) podemos determinar el valor óptimo de la corriente de acuerdo al valor de voltaje óptimo establecido en la figura 8(b). En la figura 9(b) se muestra el punto de operación de la variable óptima de corriente de acuerdo a la potencia máxima generada por los tres diferenciales de temperatura, ΔT, analizados.
4.2 Termogenerador eléctrico a escala micrométrica
En la figura 10 se presenta el TEG (𝜇m) diseñado de acuerdo a los parámetros definidos en la tabla 1. En la Figura 10 (a) se observa la cantidad de 242 termopares encontrados en el área definida de 1 cm² conformada por un total de 242 columnas de Bi2Te3 tipo-N y 242 de Bi2Te3 tipo-P intercaladas entre sí, conectadas eléctricamente en serie por los electrodos de cobre y térmicamente en paralelo por las placas de tungsteno. Además, en la figura 10(b) se definen las condiciones de frontera de acuerdo a la figura 5.
La dispersión de temperatura y potencial eléctrico a través de la estructura del TEG (μm) para un ΔT de 15 ºK, se presentan en la figura 11.
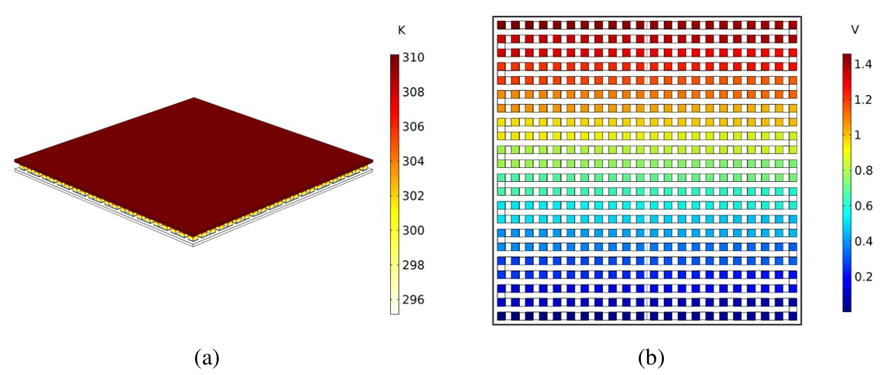
Figura 11 (a) Dispersión de la temperatura y (b) dispersión de potencial eléctrico para el TEG (μm).
Las gráficas de la figura 12 presentan la relación entre el valor de la RL y la potencia y el voltaje generado en el módulo TEG (μm) de acuerdo a los 3 valores de ΔT analizados, en azul, ΔT = 5 ºK, en verde, ΔT = 10 ºK, y en rojo, ΔT = 15 ºK. En la Figura 12 (a) se observa la potencia en función a la RL con una potencia máxima generada para una RL = 22 Ω. En la Figura 12 (b) podemos determinar el valor del voltaje de operación óptimo producido en función del valor de la RL relacionada con la potencia máxima generada para cada ΔT analizado.
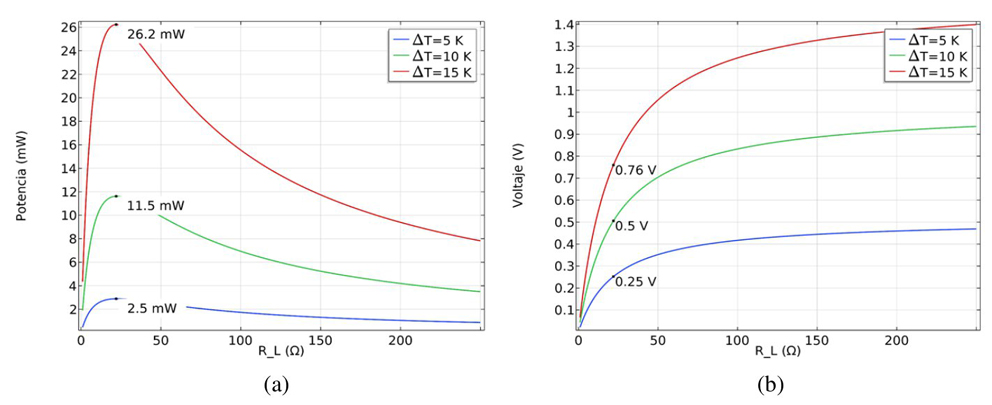
Figura 12 Gráficas para el TEG (μm) en función a la resistencia de carga. En (a) potencia vs. resistencia de carga y (b) voltaje vs. resistencia de carga.
De la misma manera podemos caracterizar el funcionamiento del TEG (μm) de acuerdo a la corriente óptima para determinar la potencia máxima generada. En la figura 13 se presentan los gráficos del voltaje y la potencia en función de la corriente. Para cada uno de los gradientes de temperatura, ΔT, analizados, en la figura 13(a) podemos determinar el valor óptimo de la corriente de acuerdo al valor de voltaje óptimo establecido en la figura 12(b). En la figura 13(b) se muestra el punto de operación de la variable óptima de corriente de acuerdo a la potencia máxima generada por los tres diferenciales de temperatura, ΔT, analizados.
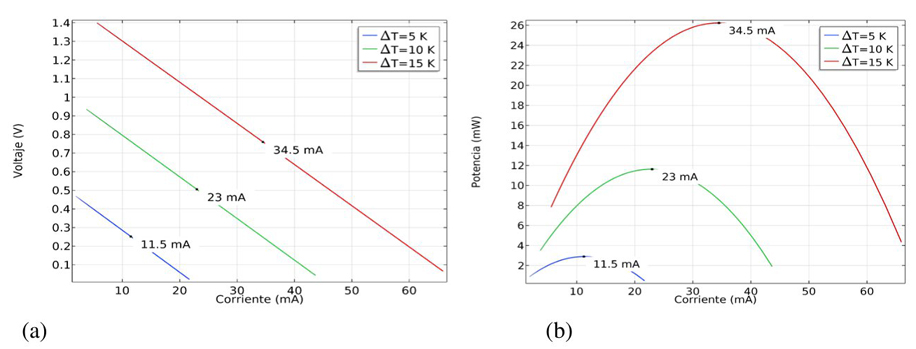
Figura 13 Gráficas para el TEG (μm) en función a la corriente. En (a) corriente vs. voltaje (b) corriente vs. potencia.
En la tabla 4 se resumen los resultados de voltaje y corriente óptimos, además de la potencia máxima evaluada de acuerdo a los parámetros de ΔT y RL, de acuerdo a la tabla 3, para cada una de las estructuras diseñadas.
5. Discusiones
Uno de los aportes de este trabajo es establecer un procedimiento estándar en la simulación de materiales TEG y los puntos principales que deben considerarse para mejorar la eficiencia energética de las estructuras diseñadas, aunque sí encontramos trabajos que realizan estudios de este tipo, la forma en la que establecen las simulaciones en programas de cómputo como COMSOL MultiphysicsⓇ, a veces no es descrita, dejando una brecha entre los resultados experimentales y su modelado numérico.
En este trabajo se estableció el análisis de la simulación de dos estructuras TEG a diferentes escalas y como estas permiten la generación de energía aprovechando una diferencia de temperatura, ΔT, de hasta 15 ºK, de acuerdo a la temperatura corporal normal.
Como se observa en la tabla 4 se establece que el número de termopares, así como las dimensiones de estos, son factores que determinan la potencia máxima de los TEG, se observa como la estructura micrométrica bajo una misma área de aplicación logra una potencia superior a la milimétrica en los tres gradientes de temperatura considerados, con 5 veces la potencia máxima para 5 grados, 5.75 veces más para 10 grados y 5.82 veces para 15 grados.
Trabajos como este nos permite visualizar, diseñar y analizar diferentes estructuras termogeneradoras en diferentes escenarios, con una amplia gama de materiales y configuraciones. Dentro de los parámetros que generalmente se evalúan de los TEG son la cantidad de elementos involucrados, i.e., cantidad de termopares, su dimensión, el área transversal y la longitud de cada una de las columnas, los materiales semiconductores, el tipo de diseño estructural, entre otras. Para el caso de este trabajo se determinó un área de trabajo constante de 1 cm2 para la cual se diseñaron dos estructuras TEG convencionales modificando el área transversal y la altura de las columnas, así como el número de termopares. En la tabla 4 se observa el desempeño energético de ambos dispositivos, donde se aprecia que la estructura a escala milimétrica (TEG mm) es menos eficiente en términos de potencia, esto es apoyado por varias investigaciones que establecen que, tanto el tamaño del TEG como la longitud de las piernas, no son parámetros importantes que logren modificar la potencia del dispositivo, sino que, como lo establecen en [20], la cantidad de termopares y el área transversal de estas estructuras son los parámetros directamente relacionados con la generación de potencia energética. Lo anterior es reafirmado en [32] donde demostraron que la longitud de los termopares debe estar en un rango de 100 a 300 μm para un máximo rendimiento energético dependiendo de la sección transversal de cada una de las piernas del TEG, lo que concuerda con nuestra estructura micrométrica y su ventaja sobre la estructura milimétrica. Las dimensiones evaluadas demuestran que mientras exista un número mayor de termopares evaluados en una misma área existirá una mayor potencia eléctrica, esto es apoyado en [24].
La importancia de este trabajo de simulación recae en el hecho de que el acceso a herramientas de softwares de análisis numérico, como lo es COMSOL MultiphysicsⓇ, permiten modelar estructuras novedosas y determinar los parámetros básicos para su funcionamiento óptimo [33]. Se debe mencionar que el diseño de dispositivos TEG aún se encuentra en constante cambio. Hoy día se han diseñado estructuras TEG flexibles que se adapten a las diferentes zonas del cuerpo humano mediante materiales poliméricos para los cuales se han realizado simulaciones con el módulo de mecánica de sólidos para analizar el desgaste de las estructuras, además de su desempeño [34-36].
No obstante, el modelado numérico de estos dispositivos nos permite determinar las dimensiones estructurales, materiales y parámetros esenciales como lo son el valor de la resistencia de carga (RL), el voltaje y la corriente óptima, para lograr una mejor conversión térmico-eléctrica. Además, de forma indirecta nos permite seleccionar el método de fabricación de acuerdo a la geometría diseñada. El estudio en cuestión abre las puertas para el diseño y la fabricación de dispositivos TEG de acuerdo a los datos simulados para un gran número de aplicaciones biomédicas como los TEG integrados en la vestimenta [33, 34], o para la autoalimentación energética de dispositivos médicos portátiles [37].
6. Conclusión
El acceso a herramientas de simulación que nos permitan experimentar con materiales y estructuras bien definidas, nos abre un campo de conocimiento para el diseño de dispositivos portátiles y autónomos para la generación de energía. En este caso se analizaron dos estructuras TEG, para las cuales se definieron materiales, dimensiones y diferenciales de temperatura, donde se evaluaron los parámetros eléctricos para obtener la eficiencia energética de cada uno de ellos. Se confirmó que las dimensiones y el número de termopares son factores que afectan a la potencia máxima que son capaces de producir este tipo de dispositivos. El diferencial de temperatura, según los resultados obtenidos, es otro parámetro importante para la eficiencia energética, aunado a la cantidad de los termopares, y la longitud y el área transversal de las columnas. En este trabajo se enfatizó en la generación de una metodología clara y reproducible, exponiendo las consideraciones necesarias para realizar una simulación válida de este tipo de dispositivos. La metodología desarrollada abre un campo de conocimiento para la evaluación del diseño estructural, y los materiales necesarios, para determinar los parámetros óptimos que den como resultado una alta eficiencia energética en dispositivos de generación de energía autónoma.











 nueva página del texto (beta)
nueva página del texto (beta)











