Prediction of rms charge radius of proton using proton-proton elastic scattering data at 													s											 = 2.76 TeV

Zahra, S.; Shafaq, B.; Zahra, S.; Shafaq, B.

doi:10.31349/revmexfise.67.491

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de física

versión impresa ISSN 0035-001X

Rev. mex. fis. vol.67 no.3 México may./jun. 2021 Epub 21-Feb-2022

https://doi.org/10.31349/revmexfise.67.491

Research

High Energy Physics

Prediction of rms charge radius of proton using proton-proton elastic scattering data at s = 2.76 TeV

S. Zahra^a

B. Shafaq^b

^{^a}Department of Physics, DSNT, University of Education, Lahore, Pakistan. e-mail: sarwat.zahra@ue.edu.pk

^{^b}CHEP, University of the Punjab, Lahore, Pakistan.

Abstract

Using proton-proton elastic scattering data at s=2.76 TeV and squared four-momentum transfer 0.36 < -t > 0.76 (GeV/c)² for 13 σ_Beam distance and 0.07 < -t < 0.46 (GeV/c)² for 4.3 σ_Beam distance, the electromagnetic form factor of proton is predicted. The simplest version of Chou-Yang model is employed to extract the form factor by fitting experimental data of differential cross section from TOTEM experiment (for 13 σ_Beam and 4.3 distance) to a single Gaussian. Root mean square charge radius of proton is calculated using this form factor and is found to be equal to 0.91 fm and 0.90 fm, respectively. This result is in good agreement with experimental data and theoretically predicted values.

Keywords: Chou-Yang model; p-p scattering; electromagnetic form factor of proton

1.Introduction

The structure of particles can be probed with the help of scattering experiments. The high energy scattering processes are now approachable present us with an opportunity to examine the hadronic structure at higher energies ¹^-⁹. Among hadrons, the proton structure has remained a topic of interest between researchers since its discovery. Proton’s radius is a prime problem in the study of its structure. The root-mean-square (rms) radius of a proton can be experimentally measured by two methods; electron proton scattering ¹⁰ and atomic spectroscopy technique. In hydrogen spectroscopy, two methods are adopted: one by using atomic hydrogen ¹¹ and a second by using muonic hydrogen ¹²; both of these methods give contradictory results, giving rise to the so-called “proton radius puzzle”. There are many theoretical approaches to find out the rms radius of proton, including MIT Bag model ¹³, self-consistent model ¹⁴, by using Lattice QCD ¹⁵^-¹⁷, etc.

The form factor also plays a dynamic role in the study of hadronic structure. It is related to the distribution of matter inside a hadron. Theories claiming to explain the structure of hadrons must be able to calculate their form factors from first principles. Continuous efforts of decades led the researchers to obtain the form factors of proton from different calculation schemes, as discussed in ¹⁸^-²². Experimentally, the magnitude of the form factor is determined by the ratio of the measured cross-section to the Mott cross-section: (dσ/dΩ)exp=(dσ/dΩ)Mott*⋅|F(q2)|2. One therefore measures the cross-section for a fixed beam energy at various angles (and thus different values of |q|) and divides by the calculated Mott cross-section.

In this work, proton-proton elastic scattering data from TOTEM experiment ⁹ is used to calculate the proton form factor employing the simplest version of Chou-Yang model. The Chou-Yang model ²³^,²⁴ is a geometrical model. In this model two hadrons are considered to be scattering elastically and are supposed to be translucent objects passing through each other without attenuation. The differential cross section (dσ/dt) and total cross-section (σ) are the two measuring quantities involved in such processes. Let us consider two hadrons A and B, scattering elastically (A+B→A+B). Let aAB(t) represent the asymptotic scattering amplitude. Here we are interested in a case, where Gaussian (in t) could be used to approximate the differential cross section. In this situation the differential cross section is written as

dσdt=αeβt. (1)

Hadron’s radius is associated to the form factor by the relation FA(t)=1-(1/6ℏ2)t⟨r2⟩. The product of both form factors (F _A(t)) and F _B(t)) of two scattering hadrons A and B is given as:

FA(t)FB(t)=constant ×∑n=1∞1nαπn/21βnβneβt/2n, (2)

(for details see Ref. ²⁵). This relation is very useful for finding out the form factor of scattering hadrons. Many form factors of proton were suggested by researchers at lower values of s ²⁶^-²⁸.

2.Calculations

In this work recent data of elastic proton-proton scatteringat s=2.76 TeV from TOTEM experiment ⁹ is used. Although the same procedure has been adopted in ¹⁸ for finding out form factor and rms radius of proton by using the data from TOTEM at s=8 TeV. Here elastic proton-proton data of two different kinematical regions is analyzed at s=2.76 TeV which would be highly beneficial for getting precise results. The experimental setup of TOTEM experiment is explained in Ref. ⁹, where one of the data sets of differential cross section has been obtained by placing Roman Pot detectors at 13 times the transverse beam size (σ_Beam). This setup allowed to measure elastic differential cross section at t = 0.36 GeV² to 0.74 GeV². The second data set was obtained by inserting Roman Pot detectors at 4.3 times the transverse beam size and measured elastic differential cross section at t = 0.07 GeV² to 0.45 GeV². The differential cross section data plotted against -t for 13 σ_Beam and 4.3 σ_Beam distance, and fitted to a single Gaussian, shown in Fig. 1 and 2, respectively.

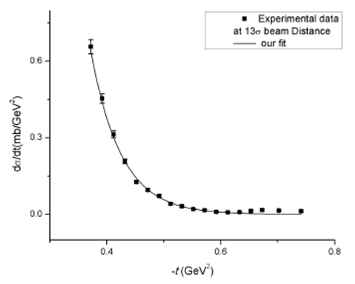
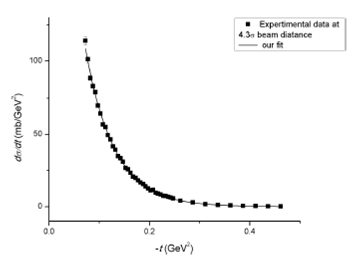
Figure 1 Fitting of differential cross section data of protonproton elastic scattering at s=2.76 TeV ( for 13 σ_Beam distance) to a single Gaussian.

Figure 2 Fitting of differential cross section data of protonproton elastic scattering at s=2.76 TeV (for 4.3 σ_Beam distance) to a single Gaussian.

The most appropriate values of α1,β1 and α 2 , 𝛽 2 are found. Where α1,β1 are the fitted parameters for differential cross section data at 13 𝜎 Beam distance and are for 4.3 σ_Beam distance. These fitted parameters given in Table I.

Table I Fitted parameters for two set of data, i.e., for 13 σ_Beam and 4.3 σ_Beam distance

α_j

(mb−1/GeV / c )

β_j (GeV )^-2

Adj. R-squared for fit

683.06 ± 228.29

−18.75 ± 0.76886

0.96907

375.62 ±4.09935

-17.15±0.0806

0.99914

The measure of goodness of fit is determined by R-square, given in Table 1. Which shows that our fit is 100% successful in both set of data. These values of α and β are used in Eq. (2) directly, and a computer program is used to solve this equation for finite values of n. The square of form factors of proton is found to be equal to

(Fjp(t))2=δj∑i=12ajiebjit. (3)

Here j = 1 and 2 for differential cross section data at 13 σ_Beam and 4.3 σ_Beam distance respectively. δj is the normalization constant. Computed values are given in Table II and Table III.

Table II Computed values of a_ji and b_ji .

	For 13 σ_Beam distance j=1		For 4.3 σ_Beam distance j=2
i	a_ij	b_ij	a_ij	b_ij
1	2:898290	-18:75452	-1:742644	-17:1527
2	14.74531	-9:37726	10.93454	10.93454

Table III Computed values of δ_j .

	δ_j
For 13 σ_Beam Distance	0.2905
For 4.3 σ_Beam Distance	0.3298

Using electromagnetic form factor from (3) we can easily compute rms charge radius of proton by using following relation ⟨r2⟩=6ℏ2(dF(t)/dt)|t=0. We have therefore computed ⟨rp⟩=0.91 fm and ⟨rp⟩=0.90 fm for 13 σ_Beam and 4.3 σ_Beam distance respectively which is in good agreement with the experiment ⟨rp⟩=0.84±0.00039 fm ²⁹.

3.Discussion

The Chou Yang model is successful in its predictions for elastic scattering process at higher as well as the lower values of s. The proton electromagnetic form factor is obtained at low squared momemtm transfer, i.e., 0.36<-t<0.76 (GeV/c)²

and 0.07<-t<0.46 (GeV/c)², but high centre-of-mass energy i.e s=2.76 TeV. Figures 1 and 2 show the points of the experimental data from TOTEM ⁹ represented by squares, whereas our fit is drawn with a solid line. We have obtained the most suitable fit. Figure 3 shows the comparison plot of our predicted form factor for both sets of data, where the dotted line shows the form factor for 13 σ_Beam distance data and solid line shows the form factor predicted for 4.3 σ_Beam distance. The novel aspect of this work is that the simplest method is employed and our calculated rms charge radius of proton that agree well with experiment and theory. A comparison of calculated values is given in Fig. 4.

Figure 3 Form factor of proton predicted (for 13 σ_Beam distance and 4.3 σ_Beam distance).

Figure 4 Comparison of calculated rms radii.

References

1. G. Antchev et al., Proton-proton elastic scattering at the LHC energy of √s= 7 TeV, EPL. 95 (2011) 41001. 10.1209/0295-5075/95/41001. [ Links ]

2. G. Antchev et al., First measurement of the total protonproton cross-section at the LHC energy of √s= 7 TeV, EPL. 96 (2011) 21002. https://doi.org/10.1209/0295-5075/96/21002. [ Links ]

3. G. Antchev et al., Luminosity-Independent Measurement of the Proton-Proton Total Cross Section at √s = 8 TeV, Phys. Rev Letts. 111 (2013) 012001. https://doi.org/10.1103/PhysRevLett.111.012001. [ Links ]

4. TOTEM Collaboration, Evidence for non-exponential elastic proton-proton differential cross-section at low |t| and p √s = 8 TeV by TOTEM, Nucl. Phys. B. 899 (2015) 527. https://doi.org/10.1016/j.nuclphysb.2015.08.010 [ Links ]

5. G. Antchev, et al., Measurement of elastic pp scattering at √s = 8 TeV in the Coulomb-nuclear interference region: determination of the p-parameter and the total crosssection, EPJC. 76 (2016) 661. https://doi.org/10.1140/epjc/s10052-016-4399-8. [ Links ]

6. Gp. Antchev, et al., First determination of the p-parameter at √s = 13 TeV: probing the existence of a colourless C-odd three-gluon compound state, EPJC. 79 (2019) 785. https://doi.org/10.1140/epjc/s10052-019-7223-4. [ Links ]

7. G. Antchev et al., Elastic differential cross-section measurement at root s = 13 TeV by TOTEM, EPJC. 79 (2019) 861. https://doi.org/10.1140/epjc/s10052-019-7346-7 [ Links ]

8. G. Antchev, et al., First measurement of elastic, inelastic and total cross-section at √s = 13 TeV by TOTEM and overview of cross-section data at LHC energies, EPJC. 79 (2019) 103. https://doi.org/10.1140/epjc/s10052-019-6567-0 [ Links ]

9. G. Antchev et al., Elastic differential cross-section d sigma/dt at root s = 2:76 TeV and implications on the existence of a colourless C-odd three-gluon compound state, EPJC. 80 (2020) 91. https://doi.org/10.1140/epjc/s10052-020-7654-y. [ Links ]

10. J. C. Bernauer, et al., Electric and magnetic form factors of the proton, Phys. Rev. C, 90 (2014) 015206. https://doi.org/10.1103/PhysRevC.90.015206 [ Links ]

11. P. J. Mohr, B. N. Taylor, and D. B. Newell, CODATA recommended values of the fundamental physical constants: 2006, J Phys Chem Ref Data. 37 (2008) 1187. https://doi.org/10.1063/1.2844785. [ Links ]

12. A. Antognini, et al., Proton Structure from the Measurement of 2S-2P Transition Frequencies of Muonic Hydrogen. Science 339 (2013) 417. 10.1126/science.1230016. [ Links ]

13. P. K. Chatley, C. P. Singh, and M. P. Khanna, Charge radii of proton and M 1 radiative transitions of hadrons in a bag model with variable bag pressure. Phys. Rev. D. 29 (1984) 96. https://doi.org/10.1103/PhysRevD.29.96. [ Links ]

14. S.G. Fedosin, The radius of the proton in the self-consistent model. Had. Jour. 35 (2012) 349. [ Links ]

15. N. Hasan et al., Computing the nucleon charge and axial radii directly at Q² = 0 in lattice QCD, Phys. Rev. D. 97 (2018) 034504. 10.1103/PhysRevD.97.034504 [ Links ]

16. F. M. Stokes, W. Kamleh, and D. B. Leinweber, Elastic form factors of nucleon excitations in lattice QCD, Phys. Rev. D. 102 (2020) 014507. https://doi.org/10.1103/PhysRevD.102.014507 [ Links ]

17. Y. C. Jang, R. Gupta, H. W. Lin, B. Yoon, T. Bhattacharya, and PNDME Collaboration, Nucleon electromagnetic form factors in the continuum limit from (2 + 1 + 1)-flavor lattice QCD, Phys. Rev. D. 101 (2020) 014507. https://doi.org/10.1103/PhysRevD.101.014507 [ Links ]

18. S. Zahra, and H. Rashid, Predictions of the Chou-Yang Model for pp Scattering at √s = 8 TeV, Chin. Phys. Letts. 36 (2019) 061201. 10.1088/0256-307X/36/6/061201 [ Links ]

19. C. A. Dominguez, Electromagnetic form factors of hadrons in quantum field theories, AIP Conference Proceedings (Vol. 1056, No. 1, 23-30), (2008) American Institute of Physics. https://doi.org/10.1063/1.3013047 [ Links ]

20. O. D. Dalkarov, P. A. Khakhulin, and A. Y. Voronin, On the electromagnetic form factors of hadrons in the time-like region near threshold, Nucl. Phys. A. 833 (2010) 104 10.1016/j.nuclphysa.2009.11.015 [ Links ]

21. D. B. Leinweber, et al., Strange electric form factor of the proton, Phys. Rev. Letts. 97 (2006) 022001, https://doi.org/10.1103/PhysRevLett.97.022001 [ Links ]

22. J. J. Murphy, I. I., Shin, Y. M. and D. M. Skopik, Proton form factor from 0.15 to 0.79 fm2, Phys. Rev. C. 9 (1974) 2125. https://doi.org/10.1103/PhysRevC.9.2125 [ Links ]

23. T. T. Chou, and C. N. Yang, Model of elastic high-energy scattering, Phys. Rev. 170 (1968) 1591. https://doi.org/10.1103/PhysRev.170.1591 [ Links ]

24. A. W. Chao, and C. N. Yang, Opaqueness of pp collisions from 30 to 1500 GeV/c, Phys. Rev. D. 8 (1973) 2063. https://doi.org/10.1103/PhysRevD.8.2063 [ Links ]

25. S.-Y. Lo., Geometrical Pictures in Hadronic Collisions: A Reprint Volume, (World Scientific, 1987). Chap. 4, p. 37 [ Links ]

26. L. Durand III, and R. Lipes, Diffraction Model for High-Energy pp Scattering, Phys. Rev. Letts. 20 (1968) 637. https://doi.org/10.1103/PhysRevLett.20.637 [ Links ]

27. J. G. Rutherglen, in Proceedings of the 4th International Symposium on Electron and Photon Interactions at High Energies, Liverpool, (1969) Sept. 14-20, Ed. by D. W. Braben (Liverpool Daresbury, Univ. of Glasgow), p. 163. [ Links ]

28. M. Saleem, and I. A. Azhar, Generalized Chou-Yang Model for p(p-) and Λ(Λ-) p Elastic Scattering at High Energies, EPL. 6 (1988) 201. 10.1209/0295-5075/6/3/003 [ Links ]

29. P. A. Zyla et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2020 (2020) 083C01, [ Links ]

30. H. Fleurbaey, New measurement of the 1 S- 3 S transition frequency of hydrogen: contribution to the proton charge radius puzzle, Phys. Rev. Letts. 120 (2018) 183001. 10.1103/PhysRevLett.120.183001 [ Links ]

31. G. Lee, J.R. Arrington, and R.J. Hill, Extraction of the proton radius from electron-proton scattering data, Phys. Rev. D. 92 (2015) 013013. https://doi.org/10.1103/PhysRevD.92.013013 [ Links ]

32. Sick, Ingo. Proton charge radius from electron scattering, Atoms 6 (2018) 2. https://doi.org/10.3390/atoms6010002 [ Links ]

33. D. Borisyuk, Proton charge and magnetic rms radii from the elastic ep scattering data, Nucl. Phys. A. 843 (2010) 59. https://doi.org/10.1016/j.nuclphysa.2010.05.054 [ Links ]

34. P.G. Blunden, and I. Sick, Proton radii and two-photon exchange, Phys. Rev. C. 72 (2005) 057601. https://doi.org/10.1103/PhysRevC.72.057601 [ Links ]

35. I. Sick, On the rms-radius of the proton, Phys. Letts. B. 576 (2003) 62, https://doi.org/10.1016/j.physletb.2003.09.092 [ Links ]

Received: October 03, 2020; Accepted: January 18, 2021

This is an open-access article distributed under the terms of the Creative Commons Attribution License