1 Introduction

During the past several decades, much effort has been devoted to investigate the phase transitions and critical phenomena. The various Ising systems, consisting of magnetic spins, is the simplest systems showing phase transitions and critical phenomena at finite temperature. The classical spin-1/2 one-dimensional (1D) Ising model was suggested by Lenz ^[1]. The exact solution of the 2D spin-1/2 Ising model in the absence of an external field was found by Onsager ^[2]. To date, the 3D spin-1/2 Ising model remains unsolved exactly, but there are approximation solutions were studied using numerical methods like Monto Carlo simulations ^[3-5].

The spin-1 Ising model (Blume-Capel (BC) model) is more suitable than spin-1/2 model, so it was used to study the phase transitions occurring in the systems of three states ^[6-8]. The model has been solved exactly on a honeycomb lattice ^[9-14]. The results of the spin-1 Ising model has been extended to the spin-3/2 Ising model ^[15-18]. Later, several works have analysed the critical properties based on the BC model ^[19-21].

The quantum Heisenberg model ^[22,23] is a quantum mechanical model analogue to the ising model. It was used to study the critical properties of magnetic systems, in which the spins are treated quantum mechanically. The isotropic Heisenberg model, both in its original quantum version and in its classical counterpart, represents one of the most powerful physical models applied to magnetic systems undergoing phase transitions ^[24-27].

The systems spin-1/2 and spin-1 have been studied extensively, based on different approaches like mean-field approximation (MFA), effective-field theory (EFT), renormalization group (RG) techniques, ϵ- expansion series expansions, Monte Carlo simulations ^[28-31]. However, the transfer matrix method which was developed mainly by Kramers and Onsagar ^[32,2] is the most extended technique due to its wide general use across many physical models ^[33-36]. But there is a lack of works when we take into account models of high order spin values.

Here, we use the transfer matrix technique to study analytically the critical behavior of the Ising model with arbitrary spin s in the absence and presence of a magnetic field. Although the critical temperature of the one-dimensional Ising model is TC=0, it displays non-trivial features in its asymptotic critical behavior as the critical point is approached ^[37-39]. Our aim will be twofold; first, to study the affect of the order of spin s on the thermodynamic and the magnetic properties of the model, and second, to investigate the asymptotic behavior of these properties when the temperature T→0, i.e, close to the critical temperature TC and when T→∞.

The paper is organized as follows. In Sec. 2, we describe how the model can be formulated and solved for arbitrary spin. Our main results of the internal energy and the entropy in the absence of a magnetic field are given in Sec. 3. The asymptotic behavior of the magnetization and the susceptibility as a function of the temperature and the field is analyzed in Sec. 4. The paper closes with a short discussion given in Sec.5.

2 The model

The Ising model for of N spins ( σi,i=1,…,N) with ferromagnetic ( J>0) coupling between the nearest neighbors and with arbitrary spin s is defined in the presence of a magnetic field h, by the interaction energy

where σi∈{s,s-1,⋯,-s+1,-s} and takes 2s+1 values. As usual, the partition function of the Ising model is given by the sum over all spin configurations

where β=(kBT)-1 (kB is the Boltzmann constant and T is the absolute temperature).

We can solve the model by using the method of Kramers-Wannier transfer method, in which one has to construct transfer-matrix and obtain the eigenvalues of this matrix. In the periodic case, the transfer matrix takes the form

where K=βJ and H=βh are the reduced nearest neighbor spin-spin coupling interactions and the reduced magnetic field, respectively. In this approach, the partition function is obtained by calculating the trace of the matrix product

where λs,j denote the eigenvalues of the transfer matrix for arbitrary spin s. As we know, the critical behavior of the model appears in the thermodynamic limit N→∞, so the bulk free energy is simply given by the largest transfer-matrix eigenvalue λmax=max{λs,1,λs,2,⋯,λs,2s+1}

In this case all the bulk thermodynamical parameters such as internal energy u, entropy S, magnetization m and susceptibility χ can be construct in terms of λmax:

In the next section, using the (5)-(7) we investigate the critical behavior of the internal energy and the entropy for the cases s = 1/2, s = 1 and s = 3/2 in the absence of the magnetic field (H = 0). In section 4, we study the behavior of the (8)-(9) in the presence of the magnetic field.

3 Critical behavior in the absence of the field

By direct calculation of the eigenvalues of the transfer matrix, one obtains for s = 1/ 2

In the case of s = 1, the eigenvalues are

Finally, for s = 3/2, the eigenvalues are given by

where (η,ζ)=(+,+),(+,-),(-,+),(-,-) for j = 1,2,3,4. It can be checked by plotting the eigenvalues against K that λmax=λs,1.

Using the eigenvalues (10)-(12), one easily obtains the following exact expressions

where

and

Now, we were able to obtain the asymptotic behavior of the internal energy and the entropy when T→0 and T→∞:

The changes in the internal energy and the entropy of the model with respect to temperature for different spin (1/2, 1 and 3/2) are given in Fig. 1. Results show that the internal energy converges to the zero at higher temperature values, while becomes constant (-s2) as T→0. When the temperature increases, the entropy increases until reaches to ln(2s+1) and goes to zero at low temperature. Also, We notice that the internal energy and the entropy are affected by increasing the order of spin s.

Figure 1 a) Internal energy and b) Entropy as a function of temperature for spin s = 1/2, 1 and 3/2 in the absence of magnetic field. 

4 Critical behavior in the presence of the external field

The eigenvalue of the transfer matrix (3) in the presence of a magnetic field can be obtained analytically for some values of the spin s. Here, we investigate only the two cases for order of spin (s=1/2 and s=1). The eigenvalues take the expressions

and

Where

Using the formulas (8)-(9) and (17)-(18) we can calculate the magnetization and susceptibility as a function of T and H.

In the thermodynamic limit N→∞, we obtain the well-known bulk magnetization and susceptibility for the system of spin-1/2 ^[40]:

The exact expressions for the magnetization and the magnetic susceptibility for the spin 1 and spin 3/2 are very cumbersome, so we will not bring them out here. For The other cases of spin s > 2 it would be very difficult to obtain the eigenvalues of the transfer matrix analytically. Therefore the partition function and the bulk free energy can be calculated numerically.

The behavior of the magnetization and the magnetic susceptibility as a function of the temperature for the spin s = 1/2, 1 at fixed field h = 0.5 is plotted in Fig. 2. It is clear that the maximum magnetization value for s = 1/2 system is 0.5, while the maximum magnetization value for s = 1 system is 1.

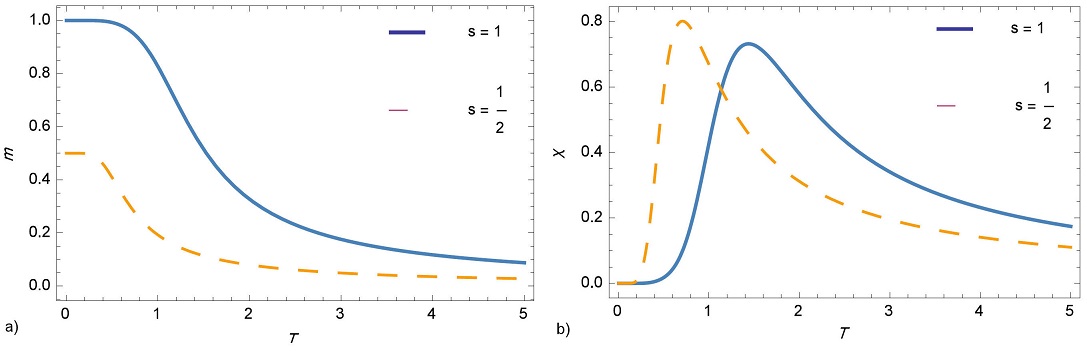
Figure 2 a) Magnetization and b) susceptibility as a function of temperature for spin s = 1/2 and 1 at a magnetic field h = 0.5. 

The field dependence of the magnetization and the magnetic susceptibility is plotted for the spin-1 system in Fig. 3 for some values of T = 1,3 and 5. We observe that the magnetization behaviour with the change of the magnetic field is more smooth with the increase of the temperature and becomes a step function in the limit of T→0 corresponding to a ferromagnetic phase. The susceptibility peaks show that the maximum of χ(T,H) is larger for low temperature and diverges at H=0 as T→0. We can see by computing the susceptibility for H = 0 and low T, that

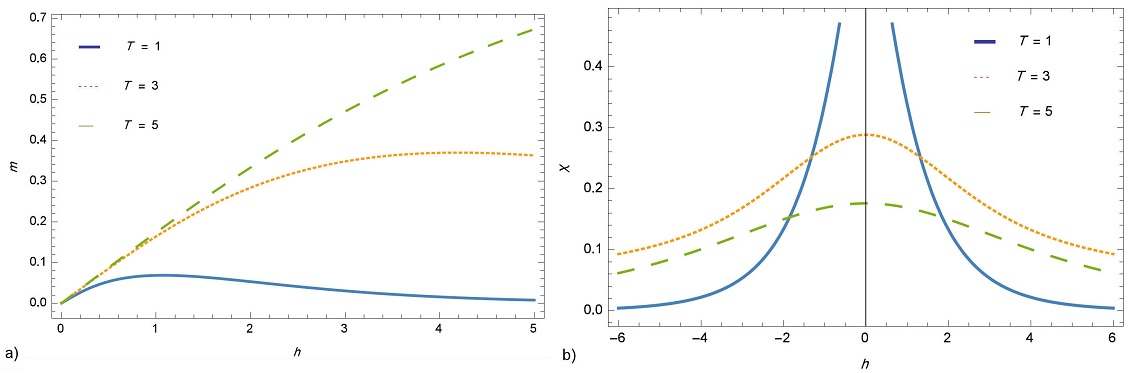
Figure 3 The field dependence of a) magnetization and b) susceptibility for spin s = 1 at three values of temperature T = 1,3 and 5. 

Thus χ divergence as T→0 and hence the well defined value γ=1 of the susceptibility exponent is obtained ^[37].

5 Conclusions

We have considered the one dimensional Ising model with arbitrary spin in the absence (presence) of a magnetic field. The system was solved analytically by the transfer matrix technique. Exact analytical results have obtained for the free energy, the internal energy, the entropy, the magnetization and the magnetic susceptibility by computing the maximal eigenvalue of the transfer matrix for some values of the order spin s.

In the absence of the magnetic field, we have studied the behavior of the internal energy and entropy for three values of the order spin s (1/2, 1 and 3/2). We have investigated the critical behavior of these properties as a function of temperature especially when T→0 and T→∞ (see (15),(16)). The behavior of the magnetization and the susceptibility has been analysed as a function of the temperature and the magnetic field and investigated near the critical point TC. Our results are consistent with the previous results for the one dimensional Ising system.