Introduction
From the last decades, advanced high strength steels (AHSS) have been extensively used for the manufacturing of structural components of auto bodies, having as a main objective weight reduction without compromising passenger safety (Altan & Tekkaya, 2013; Takahashi, 2003). Typically, these components are fabricated by using different sheet metal forming operations such as stamping and deep drawing. However, several problems arise when these materials are used for the fabrication of structural components. First, a small amount of elongation (typically around 12%-15%) is attained, leading to an excessive thinning and fracture of the material (Kardes et al., 2012; Kim et al., 2009). Second, due to the high work-hardening of the sheets, springback phenomenon takes place when the sheet is released form the tools. Forming operations with AHSS compared to conventional steel results in higher bending moments and heterogeneous stress values, leading to higher springback. This affects the geometrical and dimensional accuracy of the final components (Fallahiarezoodar et al., 2018; Farsi & Arezoo, 2007; Huang & Chen, 2005).
Springback is related to the mechanical properties of the sheet, for example, the yield stress σ Y, elastic modulus E, and work-hardening. Work-hardening is typically described by the hardening exponent n and strength coefficient K. On the other hand, the anisotropy of the sheets is evaluated by r-value (Lankford coefficients) determined at some plastic strain level. The anisotropy has a strong influence on the earing during deep-drawing operations. Moreover, the normal anisotropy r and the planar anisotropy r α affects the deep drawability and excessive thinning of the sheets (Li et al., 2020). Thus, materials with high average r and low r α anisotropy values exhibit good deep drawability and low planar anisotropy (Wang et al., 2018). Due to this, several authors have focused on developing different mechanical and heat treatment processes to improve the mechanical properties of the sheet related to the work-hardening and anisotropy.
One of these processes is intermediate annealing (IA), which consists in heating the material in a range of temperatures from 200°C to 800°C with controlled cooling inside the furnace. In this sense, Huh & Engler (2001) analyzed the effect of the IA process at different temperatures in a 17%Cr ferritic stainless-steel sheet. In their work, Huh and Engler concluded that average r-value in three angles from rolling direction (i.e., 0°, 45° and 90°) was considerable improved. Emaddodin et al. (2006) analyzed the effect of the IA time using a constant temperature of 800°C in a cold-rolled C-Mn-Si TRIP-aided sheet. The results show that the work-hardening exponent n increases with the annealing time, improving the formability of the sheet. Furthermore, the yield stress σ Y, which is related with the springback, was substantially reduced. Srivastava et al. (2006) presented the forming limit diagram (FLD) for different annealing conditions determined by an FE commercial software. The results show that the retained austenite, which is transformed in martensite with the plastic deformation, has the main influence on the formability of the sheet. Chang et al. (2017) analyzed the effect of the pre-strain and annealing process in a uniaxial tensile test. The specimens were fabricated from a CP-Ti sheet. The results show that the annealed specimens exhibit a clear yield plateau in the transition from the elastic to plastic region (Chang et al., 2017). This behavior is related to the increase in the number of dislocations in the crystallographic structure.
From the reviewed literature, even when several works are aimed to analyze the influence of heat treatment on metallic sheets, still there is a lack of information on the effect of the IA process in different types of AHSS sheets. In this work, an experimental study to analyze the influence of the intermediate annealing process on the mechanical properties of a TRIP and DP steels is presented. The anisotropy is determined by means of the r-value and is numerically described by using an anisotropic yield function. Also, to analyze the work-hardening behavior, the stress-strain curves determined from the uniaxial tensile test are presented and analyzed. Finally, from a loading-unloading-reloading sequence, the experimental and calculated evolution of the elastic modulus with the increasing plastic strain is presented and discussed.
Materials and Methodology
A transformed induced plasticity (TRIP) and a dual-phase (DP) type steel sheets of 1.1 mm and 0.8 mm thick, respectively, were used in the experiments. TRIP steel is a low alloyed multiphase steel that combine high strength and good formability. Due to the TRIP effect, the retained austenite embedded in a primary matrix of ferrite is transformed in martensite during plastic deformation process (Galán et al., 2012; Sugimoto et al., 1992). To obtain TRIP steels with an adequate or sufficiently stabilized retained austenite in the microstructure, a specific thermal processing of the rolled sheet is required, as reported by Olson & Azrin (1978). On the other hand, DP steels consist of a ferrite matrix that surrounds the islands of hard martensite, exhibiting a unique work-hardening effect with the plastic strain increasing. The chemical composition of both steel sheets used in this work are listed inTable 1.
Table 1 Chemical composition of the transformed induced plasticity (TRIP) and dual phase (DP) sheets (% Wt).
| C | Si | Mn | P | Al | B | Cr | Cu | Mo | Nb | |
| TRIP | 0.22 | 0.102 | 1.62 | 0.013 | 1.43 | 0.0002 | 0.028 | 0.015 | 0.003 | 0.001 |
| DP | 0.15 | 0.75 | 2.5 | 0.08 | 1.5 | 0.005 | - | 0.20 | - | - |
Source: Authors’ own elaboration.
Experimental procedures
Specimens
From the received sheet, uniaxial tensile test specimens were cut using electro erosion in three angles with respect to the rolling direction (i.e., 0°, 45°, and 90°). The specimens’ geometry was defined according to the ASTM E-8 standard (Standard ASTM, 2004). Once cut, the specimens were deburred to minimize the residual stresses induced from the cutting process. Next, extensometer lines and initial cross section dimensions were measured to calculate the stress-strain response and anisotropy values. The geometry of the specimen is shown in Figure 1, and the geometrical dimensions are listed in Table 2.
Intermediate annealing process
To investigate the effect of the intermediate annealing process on the elastoplastic properties and anisotropy of the sheets, isothermal heat-treatment was conducted using a Carbolite CFW 1300 furnace equipped with close-loop temperature control. The annealing temperatures used were 400°C and 800 °C. The process was conducted using a dwell time of 1 hour with a controlled cooling inside the furnace for 24 hours until room temperature was reached. The dimensions of the specimens (width and thickness) were measured before and after the heat treatment. Figure 2 shows a set of specimens during the annealing process.
Uniaxial tensile test and sheet anisotropy
To evaluate the influence of the IA on the mechanical response of the material, uniaxial tensile test experiments were performed in virgin and annealed specimens. For the experiments, a constant crosshead speed of 5 mm/min were used. The strain measurement was conducted by using a 50 mm gauge length extensometer, as depicted in Figure 3. The experiments were performed in the three rolling directions of the sheet (0°, 45°, and 90°). To assure the repeatability of the experiments, three sets of specimens were tested in each condition, and the average value is presented in the results.
To measure the planar anisotropy of the sheet, the uniaxial tensile test experiments up to an effective plastic strain of 0.1 were conducted. At this plastic strain level, the r-values r 0, r 45 and r 90 were calculated in three angles from the sheet rolling direction. To describe the planar anisotropy of the sheets, the quadratic anisotropic yield function of Hill48-r was employed in this work. For a plane stress condition, Hill48-r model is described as follows (Hill, 1948):
Here, F, G, H, and N are the anisotropy constants expressed in terms of the r α values as:
Loading-unloading-reloading sequence
The evolution of the Young’s modulus with the increasing plastic strain Ɛ P were determined from the loading-unloading-reloading experimental sequence under uniaxial stress state, as illustrated in Figure 4. The experiments were conducted under strain control up to a plastic strain of 0.125. After the experiment, the instantaneous Young’s modulus E0 to E5, corresponding to each plastic strain increment (i.e., 0.025, 0.05, 0.075, 0.10, and 0.125), were calculated. To describe the evolution of the Young’s modulus, equation 3 proposed by Yoshida was used (Yoshida & Uemori, 2002; Yoshida et al., 2002):
where E AV is the instantaneous Young’s modulus, E 0 is the initial Young modulus, Eα is the saturated Young’s modulus and ξ is constant experimentally determined.
Results
The comparative analysis of the experimental results is presented in this section. First, the true stress vs. true strain curves determined from the uniaxial tensile test in the 0° rolling direction at room temperature (RT) and annealing temperature are presented in Figure 5a and 5b for the DP and TRIP sheets, respectively. It can be observed that the stress-strain curve at room temperature for both materials exhibit a smooth transition from the elastic to the plastic deformation zone. However, a clear yield plateau is observed in the specimens with the intermediate annealing process. This behavior is related to the generation of dislocations in the grain boundaries, as reported by Le et al. (2017). Also, it can be observed that the yield stress σ Y is strongly influenced by the annealing temperature. The initial yield stress for the virgin specimen is σ Y = 440MPα. On one hand, the specimens subjected to 400 oC exhibit higher yield stress with value σ Y = 502MPα and a clear yield plateau. On the other hand, the specimens under a heat treatment of 800 oC exhibit lower yield stress with σ Y = 325MPα. This behavior is related to the recrystallization of the material with the elevated temperature, reducing its strength. Also, the work-hardening behavior is influenced by the annealing process. Here, the 800°C stress-strain curves show a reduced work-hardening of the material, exhibiting almost a linear behavior. Hence, the annealing temperature can be considered as a process to modify the mechanical properties of the sheet depending on the applications. Finally, it can be observed that the uniform elongation of the sheet is increased with the annealing temperature. This is related to the grain refinement obtained with the annealing temperature. Table 1 lists the summary of the experimental results in terms of the yield stress σ Y, tensile stress σ UT, and percentage of elongation %El.

Authors’ own elaboration.
Figure 5 Stress-strain curves determined in the rolling direction of the sheet at room temperature and IA for DP (a) and TRIP (b) steel.
Table 3 Experimental results of the uniaxial tensile test in 0°, 45°, and 90° rolling direction.
| DP | TRIP | ||||||
| Co | RD |
σY [MPa] |
σUT [MPa] |
% El |
σY [MPa] |
σUT [MPa] |
% El |
| RT | 0° | 422 | 623 | 25.6 | 434 | 723 | 22.1 |
| 45° | 433 | 645 | 23.5 | 451 | 757 | 21.4 | |
| 90° | 412 | 648 | 23.2 | 426 | 712 | 23.6 | |
| 400Co | 0° | 501 | 598 | 23.8 | 538 | 631 | 21.8 |
| 45° | 517 | 613 | 23.1 | 541 | 650 | 21.1 | |
| 90° | 537 | 622 | 22.0 | 553 | 665 | 22.9 | |
| 800Co | 0° | 328 | 447 | 22.1 | 358 | 417 | 21.3 |
| 45° | 344 | 447 | 22.9 | 372 | 422 | 20.6 | |
| 90° | 354 | 450 | 21.2 | 387 | 426 | 22.2 | |
Source: Authors’ own elaboration.
The evolution of the anisotropy with the annealing temperature and its prediction by the Hill48-r model is presented in Figure 6a and 6b for the DP and TRIP sheets, respectively. First, it can be observed from both materials that the anisotropy gradient between the 0°, AND 90° is greater at room temperature. This would cause the generation of ears and excessive thinning of the material as it is plastically deformed. However, in the annealed specimens, the anisotropy gradient is reduced as the temperature is increased. The reduction on the grain size minimizes the anisotropy effect on the sheet. On the other hand, it can be observed for both sheets that the magnitude of the planar anisotropy decreases as temperature increases, reducing the formability of the material. From the material modeling, it can be observed that quadratic Hill48-r model is able to accurately describe the anisotropy of the sheet in the three directions and for all the temperature conditions. These parameters can be used in finite element (FE) simulations of annealed components. In summary, annealing processes can be used to reduce the planar anisotropy of the sheet, leading in a homogeneous strain state when the material is deformed.
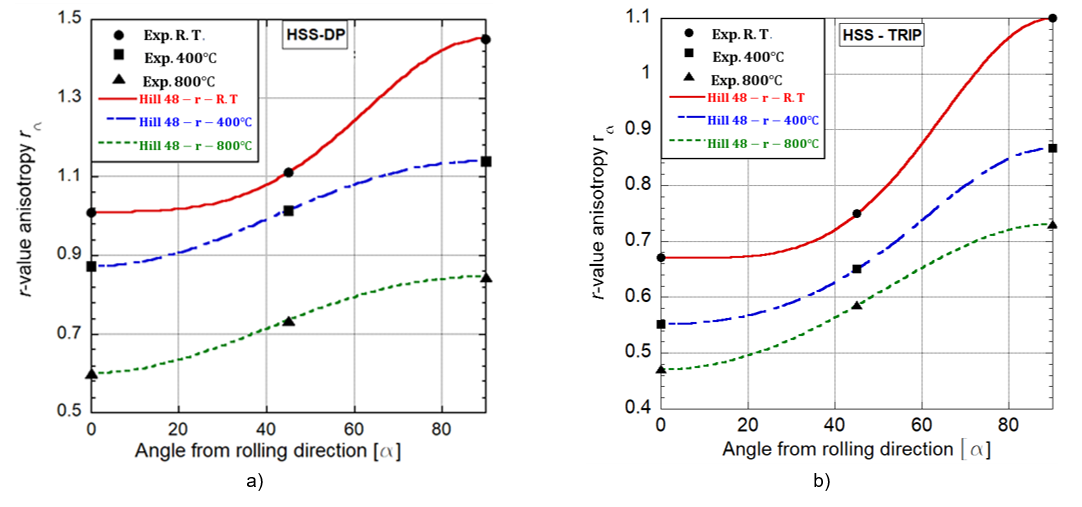
Source: Author’s own elaboration.
Figure 6 Influence of the annealing process on the r-value anisotropy for DP (a) and TRIP (b) sheets.
From the loading-unloading-reloading experimental sequence, the Young’s modulus variation with the increasing plastic strain Ɛ P is presented in Figure 7a and 7b, for the DP and TRIP sheets respectively. The Young’s modulus was determined using the 0o rolling direction specimens. First, it can be observed for the DP sheet that the initial Young’s modulus is E=195GPα for the annealed and room temperature specimen. Then, as the plastic strain increases, the Young’s modulus drastically decreases until a saturated value near to E=157GPα at Ɛ P=0.125 is obtained. However, for the annealed specimens at 400°C and 800°C, the Young’s modulus decreases to, E=151GPα and E=147GPα, respectively. This behavior is related to the generation of dislocations and free boundaries of the crystals. From the macroscopic perspective, this reduction in the Young’s modulus would influence the springback behavior of the material. On the other hand, for the TRIP sheet, an initial Young’s modulus E=198GPα is observed. Then, for the room temperature specimen, the material shows a clear stagnation value of E=158GPα. However, in the case of the annealing at 400 oC, the saturation of the Young’s modulus is not observed and continue decreasing with the plastic strain increments.
Conclusions
From the experimental results obtained in this work, the next conclusions are addressed. The mechanical properties determined from the uniaxial tensile test are highly influenced by the annealing temperature. The determined yield stress of the room temperature specimen is σ Y = 440MPα. Then, it was observed that, for the annealing process of 400°C and 800°C, the yield stress changes to σ Y = 502MPα and σ Y = 325MPα, respectively. For industrial applications, lower yield stress values represent lower springback when the material is used in metal forming applications.
The anisotropy of the sheet with the annealing process is reduced in comparison with that determined from the specimens at room temperature. The anisotropy at room temperature for the DP sheet is r0 = 0.94, r45 = 1.1 and at 800°C is r0 = 06, r45 = 0.71 and r90 = 0.84. For the TRIP sheet, the room temperature anisotropy is r0 = 0.68. r45 = 0.74 and r90 = 1.1 and at 800°C is r0 = 0.48, r45 = 0.57 and r90 = 0.72. This behavior is related to the reduction of the grain size with the increasing of the temperature, leading to a more homogeneous crystallography.
From the loading-unloading-reloading sequence, it was observed that the Young’s modulus considerable decrease with the plastic train increments. Also, the annealed specimens exhibit a lower value without saturation.
For sheet metal forming applications, the annealing process can be used to modify the mechanical properties of the HSS sheets to reduce the springback and the influence of the anisotropy.
Funding: This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.











 nueva página del texto (beta)
nueva página del texto (beta)







