Introducción
El inventario del volumen maderable o la biomasa contenidos en los bosques es considerado un proceso básico en su gestión, permite medir y monitorear a escala local los cambios que suceden en este tipo de ecosistemas (Urbazaev et al., 2018). Su realización implica la medición de árboles ubicados en unidades de muestreo de dimensión fija, comúnmente distribuidas en una red sistemática sobre un área determinada (Grafström y Ringvall, 2013). En las últimas décadas se ha impulsado el uso combinado de datos medidos en campo y datos colectados mediante sensores remotos para la realización de este tipo de inventarios (Grafström y Ringvall, 2013; Crespo-Peremarch et al., 2018).
La tecnología LIDAR (Light Detection and Ranging) aerotransportada ha demostrado utilidad para estimar variables biométricas del bosque con precisión aceptable a partir del registro de retornos (rebotes) de un haz de luz previamente emitido por un equipo especializado (Ortiz-Reyes et al., 2015; Marchi et al., 2018). Desafortunadamente, la adquisición de datos de LIDAR es costosa en comparación con datos provenientes de sensores ópticos o de radar. El costo está influenciado por el tiempo de vuelo y por la densidad de retornos por metro cuadrado que se desea registrar, los cuales a su vez varían con la velocidad, la altitud y el ancho de barrido del vuelo (Hansen Hofstad et al., 2015).
En años recientes se han estudiado estrategias para abaratar el costo de usar datos LIDAR en la estimación de inventarios forestales; particularmente la reducción de la densidad de retornos por metro cuadrado y el uso de transectos en lugar de datos de cobertura completa (Almeida et al., 2019; Ortiz-Reyes et al., 2019). Evaluaciones del efecto de la densidad de retornos en la precisión de la estimación de variables como la altura, diámetro cuadrático, área basal, volumen y biomasa, indican que las densidades óptimas varían de 0.5 m-2 a 15 m-2 en plantaciones, bosques tropicales (Hansen Hofstad et al., 2015; Silva et al., 2017; Almeida et al., 2019) y en bosques templados puros o mixtos (Treitz et al., 2012; Singh et al., 2015). Respecto al uso de datos LIDAR para solo una fracción del área a inventariar (a manera de una muestra), y a partir de esta expandir las estimaciones mediante modelos matemáticos alimentados con datos de otras imágenes de costo menor, se han publicado resultados prometedores (Ortiz-Reyes et al., 2019). Aunque el método tiene limitaciones debido a la trayectoria lineal de la plataforma que porta el instrumento (avión) (Wulder et al., 2012), éste es actualmente un procedimiento común en la selección de las muestras de campo, además de optimista para la estimación de variables de interés en el inventario (Mahoney et al., 2018; Ver et al., 2018). De acuerdo con Chen et al. (2012) y Wulder et al. (2012) la adquisición de una muestra de datos LIDAR en transectos, en combinación con un marco de muestreo apropiado, genera estadísticos precisos y de bajo costo para áreas extensas.
Los transectos LIDAR pueden incorporarse a un diseño de muestreo en dos etapas en el que las unidades de muestreo primarias (UMP) son los transectos y las secundarias (UMS) son parcelas medidas en campo (Gregoire et al., 2011; Wulder et al., 2012; Strîmbu et al., 2017). Mediante un estimador complejo en dos etapas, se puede estimar la media general de variables de interés. Para este propósito regularmente se han utilizado métodos paramétricos como la regresión lineal (Strîmbu et al., 2017) y no lineal (Saarela et al., 2015), además de modelos semiparamétricos o no paramétricos (McRoberts et al., 2011; Kangas et al., 2016).
Aunque el uso de estimadores complejos representa una solución para la estimación del inventario de variables de interés forestal a través de transectos LIDAR, paralelamente se ha propuesto la extracción de métricas derivadas de sensores ópticos para combinarlos con datos LIDAR y con ello estimar parámetros forestales a escala regional (Chen et al., 2012) y nacional. En México se han realizado estudios a escala nacional, combinando imágenes satelitales con datos LIDAR colectados en transectos para la estimación de biomasa aérea (Nelson et al., 2017; Urbazaev et al., 2018). A escala regional este enfoque se ha explorado para la estimación de biomasa aérea, carbono, riqueza y diversidad de especies en la península de Yucatán (Hernández-Stefanoni et al., 2014; Ochoa-Franco et al., 2019; George-Chacon et al., 2019; Ortiz-Reyes et al., 2019). Si bien esto demuestra el interés nacional por fomentar el uso de estas herramientas de teledetección y enfoques de muestreo para la estimación de variables forestales, su uso es todavía limitado, particularmente para la estimación de inventarios operativos.
Este estudio tuvo como propósito analizar de manera conjunta el efecto del diseño de muestreo LIDAR y la densidad de retornos por metro cuadrado sobre la precisión del inventario de área basal (AB), volumen de madera (V) y biomasa (B) en un bosque templado bajo manejo ubicado en Zacualtipán, Hidalgo.
Objetivos
Los objetivos de este estudio fueron analizar el efecto de diferentes diseños de muestreo y densidades de retornos (puntos) por unidad de área (m2) sobre la estimación del inventario de AB, V y B en áreas con datos LIDAR y combinar los resultados del mejor diseño encontrado para estimar y mapear el inventario total de AB, V y B en un predio forestal mediante estimadores de muestreo complejos asistidos por modelos aditivos generalizados (GAM).
Materiales y métodos
Área de estudio
El estudio se realizó en el área forestal que conforma el Sitio de Monitoreo Intensivo de Carbono (SMIC) en Atopixco, localizado en el municipio de Zacualtipán, Hidalgo, entre las coordenadas 20°40’17” y 20°34’51” latitud norte, 98°40’07” y 98°34’22” longitud oeste (Fig. 1). Su fisiografía comprende parte de la Sierra Alta Hidalguense y del Eje Neovolcánico. La precipitación promedio anual es de 1601 mm, con una temperatura media anual de 17 °C y clima templado húmedo con lluvias todo el año (Instituto Nacional de Estadística y Geografía [Inegi], 2017). El SMIC tiene una superficie de 900 ha cubiertas mayoritariamente de bosque coetáneo. Lo conforman rodales dominados por Pinus patula con edad variable desde 0 años hasta 31 años y algunas áreas sin intervención silvícola en los últimos 80 años (naturales) (Torres-Vivar et al., 2017).
Datos de campo: estimación de atributos forestales
Se establecieron 24 unidades de muestreo primarias (UMP) de inventario permanente con arreglo sistemático y 17 adicionales siguiendo un gradiente de años transcurridos a partir de la cosecha de los rodales para capturar la variabilidad del paisaje forestal en el área de estudio (Fig. 1). Cada UMP está conformada por subunidades o unidades de muestreo secundarias (UMS), en ellas se ubicó el centro mediante un GPS Garmin® (± 3m). Las UMS estuvieron dispuestas de forma espacial en forma de “Y” invertida como el diseño del Inventario Nacional Forestal y de Suelos (INFyS) (Comisión Nacional Forestal [Conafor], 2011). En total se dispuso de 164 UMS circulares de 400 m2, pero solo se utilizaron 96 UMS, dejando fuera del análisis aquellas que no se ubicaron dentro de los diseños propuestos. En los sitios se midió el diámetro normal (DN) y la altura total (H) de todos los árboles con DN > 7.5 cm. Con estos datos se estimó su área basal (AB; m2; Conafor, 2011), su volumen maderable (V; m3) y su biomasa (B; kg), utilizando las ecuaciones para especies latifoliadas y pinos presentadas por Cruz-Martinez (2007) y Soriano-Luna (2014), respectivamente.
Datos del sensor LIDAR
Los datos LIDAR fueron obtenidos en mayo del 2013 con el sensor Riegl-VQ480 a una altitud de 397 m, una frecuencia de 200 kHz, un ángulo de barrido de ±15º y una intensidad de retornos de 5 m-2 a 10 m-2. Los retornos registrados permitieron generar una “nube de puntos” tridimensional, la cual se constituyó como la base de datos LIDAR (Ortiz-Reyes et al., 2015). Además, se generó un modelo digital de elevación (MDE) de 1 m de resolución para normalizar las alturas de los árboles sobre el suelo. La Figura 2 muestra los pasos metodológicos generales implementados en el presente estudio. En los párrafos siguientes se detalla el procedimiento.
Diseños de muestreo LIDAR
Se definieron tres diseños de muestreo a partir de la ubicación en campo de las parcelas del inventario. Dos diseños consistieron en transectos de datos LIDAR de 200 m de ancho y 2.8 km de largo ubicados con dirección este-oeste y norte-sur (Fig. 1a y 1b, respectivamente). El tercer diseño correspondió a muestras de 400 m2 ubicadas en rodales de edad diferente (Fig. 1c), previendo que en el futuro será factible colectar este tipo de nubes de puntos LIDAR mediante sensores montados en drones. Los tres diseños de muestreo fueron recortados con la herramienta PolyClipData de la aplicación FUSION (McGaughey, 2018) de los datos LIDAR disponibles para el SMIC, utilizando el mismo número de UMS (96 sitios).
Reducción de la densidad de retornos LIDAR
En cada uno de los sitios de 400 m2 la densidad de retornos LIDAR original se redujo para simular diferentes características de adquisición de datos. Esta reducción se realizó con la función lasfilterdecimate (random) de la paqueteria lidR (Roussel et al., 2020) del software R (R Team Core, 2019). Se implementaron dos niveles de densidad: baja (0.2 m-2, 0.4 m-2, 0.6 m-2, 0.8 m-2 y 1 m-2 retornos) y alta (2 m-2, 4 m-2, 6 m-2, 8 m-2 y 10 m-2 retornos).
Métricas LIDAR
Se calcularon 40 métricas LIDAR (McGaughey, 2018) a nivel de sitio (400 m2) y de transecto para las 10 densidades de retornos evaluadas. Se utilizó una altura de corte de 3 m con el propósito de eliminar la variación (ruido) generada por la vegetación del sotobosque. Los transectos LIDAR para cada densidad de retornos evaluada fueron convertidos a formato Raster con la herramienta Csv2Grid de FUSION, con tamaño de pixel de 20 m × 20 m (400 m2), similar al tamaño de los sitios medidos en campo.
Datos multiespectrales: procesamiento de imágenes RapidEye
Se utilizaron dos imágenes RapidEye con nivel de procesamiento 3A tomadas el 23 de marzo y 13 de abril del año 2013. Estas imágenes tuvieron una resolución radiométrica de 12 bits y se reescalaron a un rango dinámico de 16 bits. La escala se realizó con un factor constante que convierte los números digitales (ND) del sensor en valores absolutos de radiancias (Planet Labs Inc, 2016). Posteriormente, se calculó la reflectancia en la parte superior de la atmósfera (TOA) conforme al procedimiento detallado por Planet Labs Inc. (2016). Las dos imágenes que cubren el área de estudio fueron normalizadas mediante el procedimiento Histogram matching (Helmer y Ruefenacht, 2005; Hong y Zhang, 2008). Este procedimiento se implementó en el software R con la función histMatch de la paquetería RStoolbox (Leutner et al., 2019).
A partir de los datos de reflectancia se calculó el índice de vegetación de diferencias normalizadas (NDVI) (Kim y Yeom, 2015) y 42 métricas de textura espectral (media, varianza, homogeneidad, contraste, disimilitud, entropía y segundo momento) y de coocurrencia de niveles de grises (GLCM) que consideran la relación espacial entre grupos de celdas adyacentes en una determinada ventana (15 × 15; Ochoa-Franco et al., 2019). El proceso se aplicó a las cinco bandas (R, G, B, Red edge e Infrarrojo) y al NDVI mediante el software R con la paquetería GLCM (Zvoleff, 2020). Posteriormente, las métricas fueron remuestreadas, con el método del vecino más cercano, para empatar el tamaño de las celdas de las imágenes con la dimensión de los sitios de muestreo en campo (400 m2), i.e., se transformó el tamaño de las celdas de 5 m × 5 m a 20 m × 20 m de resolución espacial.
Análisis estadístico: estimación de variables forestales a nivel transectos LIDAR y SMIC
Estimación de área basal, volumen y biomasa en los transectos LIDAR
Inicialmente se identificaron correlaciones relevantes entre AB, V y B calculadas a partir de datos de campo y las métricas LIDAR generadas a partir de la nube de puntos. Posteriormente se ajustaron modelos aditivos generalizados (GAM por sus siglas en inglés) para estimar, a nivel pixel (20 m × 20 m), valores de AB, V y B en el área muestreada mediante transectos LIDAR. Lo anterior con base en evidencia que señala que este tipo de modelos son más consistentes y de mejor precisión que otros modelos utilizados para estimar variables continuas (e.g. modelos lineales, no lineales, random forest) (Soriano-Luna et al., 2018). Los datos de AB, V y B colectados en campo se definieron como las variables dependientes y las métricas LIDAR representaron a los predictores. El ajuste de los modelos se realizó en la paquetería mgcv mediante la función gam del software R (Team R Core, 2019).
El efecto de la densidad de retornos sobre las estimaciones de AB, V y B a escala de sitio, se evaluó mediante el coeficiente de determinación (R2) y la raíz del error medio al cuadrado (RMSE) asociados a los modelos ajustados a partir de la validación cruzada repetida 30 veces de la muestra inicial (LOOCV). Estos valores fueron representados en diagramas de caja para comparar la variabilidad de las estimaciones y determinar la densidad de retornos LIDAR más adecuada para el mapeo de toda el área de estudio (SMIC), y en la estimación del inventario total mediante estimadores asistidos por modelos. Para comprobar si las diferencias entre las densidades de retornos simuladas y la original eran significativas, se realizó una prueba de Mann-Whitney-Wilcoxon de dos caras.
Estimación de área basal, volumen y biomasa para el SMIC con imágenes RapidEye
Los valores de AB, V y B estimados previamente para los transectos se consideraron en esta fase como variables dependientes, y como nuevos predictores los valores registrados en las cinco bandas espectrales, las métricas de textura calculadas (Zvoleff, 2020), y los valores de NDVI. Se excluyeron del análisis los pixeles con valores atípicos de las estimaciones de AB, V y B, i.e., aquellos con magnitud mayor al cuartil 3 por al menos 1.5 veces el rango intercuartil. Se eliminaron 6%, 2% y 3% de los datos para AB, V y B, respectivamente. Lo anterior para tener un mejor ajuste de los modelos a escala de área de estudio total (SMIC) y evitar sobrestimaciones.
Se comparó el uso de modelos GAM versus el algoritmo de aprendizaje automático random forest (RF), con el objetivo de identificar la mejor opción para determinar la distribución espacial de las variables de interés. Dado que el número de observaciones fue grande (7000 valores), 90% de los datos se usaron para el ajuste/entrenamiento de los modelos y 10% para la validación. Los modelos que resultaron con los mejores parámetros de bondad de ajuste (R2 y RMSE) se utilizaron para mapear en la totalidad del área del SMIC, i.e., las áreas no cubiertas por el sensor LIDAR. El ajuste de los modelos y el mapeo de las variables se realizó en el software R (Team R Core, 2019), paqueterías mgcv (ajuste GAM), randomForest y raster para la construcción de los mapas.
Estimadores muestrales e inventario total
El diseño en dos fases (Mandallaz, 2008) permitió asignar inicialmente una muestra grande n1 a la primera fase (S1), representada por los datos de transectos LIDAR (6457 celdas de tamaño de 400 m2), distribuida uniformemente dentro del área forestal. En la segunda fase (𝑆𝑆2), se dispuso de los datos de inventario de las variables AB, V y B [𝑌(𝑥2)] tomados en campo mediante una muestra más pequeña 𝑛2 (96 sitios de muestreo). Con base en las muestras n1 y n2 se ajustó un modelo de regresión GAM, identificado previamente como la mejor opción para relacionar los datos LIDAR y los datos de inventario. Para estimar la media de las variables AB, V y B, se utilizó el estimador por diferencia para el estimador en dos fases (Mandallaz et al., 2013; ecuación 1):
donde:
𝑛1: muestra intensiva en la primera fase (transectos)
𝑛2: muestra de la segunda fase (datos de campo)
𝑌(𝑥2) : valores observados en campo (𝑛2)
El estimador de varianza, de acuerdo con Mandallaz et al. (2013) y con Næsset et al. (2013), se calculó con la ecuación 2; y los residuales, dentro de esta ecuación, se calcularon con la ecuación 3.
donde:
𝑛1 y 𝑛2 se definieron anteriormente
La varianza de los valores observados en n 2 se calculó con la ecuación 4; la varianza de los residuales estimados en la muestra n 2 se calculó con la ecuación 5 y el promedio de los residuales con la ecuación 6.
Estimador en dos etapas
El diseño en dos etapas parte del supuesto de una población U que está dividida en M conglomerados {𝑈1,…,𝑈𝑀} no traslapados del mismo tamaño. En la primera etapa de muestreo se elige una muestra de m conglomerados (UMP) que corresponden a un total M. La segunda etapa consiste en seleccionar una muestra de tamaño ni (UMS) dentro de cada UMP seleccionada en la primera etapa (Mandallaz, 2008; Næsset et al., 2013). En el estudio se utilizaron los transectos LIDAR como UMP, donde el total de las celdas de 400 m2 (UMS) se considera como de tamaño Ni (Gregoire et al., 2011).
El estimador de la media en dos etapas se calcula con la ecuación 7 (Næsset et al., 2013).
donde:
M : número total de conglomerados
m : muestra de conglomerados en la primera etapa
N : total de UMS
n : muestra de UMS seleccionada en la segunda etapa
El estimador de varianza total (ecuación 8; Gregoire et al., 2011) es la suma de la variación entre todas las muestras posibles de UMP para el diseño empleado en el muestreo (ecuación 9) más la variación entre las muestras UMP dentro de cada UMP (ecuación 10).
Resultados y discusión
Los valores promedio de AB, V y B (ha-1) más altos, estimados con datos de campo, se obtuvieron en el diseño de muestreo dirección Este-Oeste seguido del diseño estratificado (Tabla 1). Del total de métricas LIDAR calculadas, la “altura media del dosel” (Elev_mean) y la “proporción de todos los retornos por encima de la media entre el total de primeros retornos” (Allretabmean _Tot1stret100) mostraron una correlación alta con el AB, V y B; alcanzando coeficientes de correlación de hasta 0.92 (Tabla 1). Estas dos métricas se utilizaron para predecir el AB, V y B en los transectos con datos LIDAR adicionando como variables las coordenadas de longitud (x) y latitud (y), las cuales contribuyeron a los modelos GAM con un efecto espacial de suavizado bivariado.
TABLA 1 Valores promedio por hectárea de área basal, volumen total y biomasa aérea estimados a partir de datos de campo (n = 96) y su coeficiente de correlación (r) respecto a las métricas LIDAR relevantes.
| Diseño | Variable | Mínimo | Máximo | Media | r | |
| Elev_mean | Allretabmean_T ot1stret100 | |||||
| AB (m2 ha-1) | 0.15 | 47.92 | 22.02 | 0.76 | 0.86 | |
| Horizontal | V (m3 ha-1) | 0.31 | 393.05 | 167.16 | 0.85 | 0.84 |
| B (Mg ha-1) | 0.16 | 281.77 | 90.82 | 0.81 | 0.81 | |
| AB (m2 ha-1) | 0.15 | 47.92 | 18.93 | 0.84 | 0.90 | |
| Vertical | V (m3 ha-1) | 0.31 | 438.80 | 143.92 | 0.88 | 0.91 |
| B (Mg ha-1) | 0.16 | 281.77 | 76.00 | 0.86 | 0.86 | |
| AB (m2 ha-1) | 0.27 | 35.84 | 19.66 | 0.87 | 0.90 | |
| Estratificado | V (m3 ha-1) | 0.56 | 362.51 | 159.19 | 0.92 | 0.89 |
| B (Mg ha-1) | 0.27 | 200.02 | 83.51 | 0.91 | 0.90 | |
AB : área basal, V : volumen, B : biomasa aérea. Elev_mean es la altura media, Allretabmean_Tot1stret100 es proporción de todos los retornos por encima de la media entre el total de primeros retornos.
La evaluación de los modelos GAM mediante validación cruzada (LOOCV) demostró que la reducción de la densidad de retornos a escala de sitio afectó la bondad de ajuste calculada, aumentando los valores de RMSE y disminuyendo el R2 en los tres diseños de muestreo implementados en densidades menores o iguales a 1 retorno por metro cuadrado. Además, los promedios de R2 calculados para los modelos de V, B y AB en las diferentes densidades de retornos oscilaron entre 0.86 y 0.90, 0.82 y 0.92, 0.76 y 0.83, respectivamente. El diseño estratificado (DE) presentó los valores promedio más bajos de RMSE (volumen = 37.01 m3 ha-1, biomasa = 18.26 Mg ha-1 y área basal = 4.97 m2 ha-1), seguido del diseño por transectos este-oeste (DH). Estos resultados demuestran que, si se utiliza el diseño estratificado, se captura la mayor variabilidad del atributo de interés. Por otro lado, de acuerdo con Wulder et al. (2012), los transectos LIDAR obtenidos de forma sistemática, operativamente resultan menos costosos en áreas grandes, sin embargo, se debe identificar el gradiente que logre capturar la mayor variación de la masa forestal dentro de cada línea de vuelo. Lo anterior puede explicar el hecho de que la variabilidad en los valores de RMSE y R2 se mantuvo constantes y simétricos en estos diseños aun en densidades bajas de retornos por metro cuadrado (Fig. 3). Los resultados obtenidos concuerdan con lo señalado por Hansen Hofstad et al. (2015), quienes indicaron que las métricas derivadas de datos LIDAR aerotransportado son confiables cuando se construyen a partir de densidades mayores a 0.5 retornos por metro cuadrado. En el mismo sentido, Treitz et al. (2012) utilizaron una densidad de 0.5 retornos por metro cuadrado para el ajuste de modelos lineales múltiples y demostraron que fue suficiente para la estimación del inventario forestal a escala de sitio en Ontario, Canadá. Conviene mencionar que el ajuste de los modelos puede aumentar si se normaliza la nube de puntos (retornos) respecto al suelo a partir de un MDE de buena calidad; este proceso fue evaluado por Silva et al. (2017), quienes encontraron que las estimaciones de biomasa a escala de paisaje se subestimaron fuertemente a densidades por abajo de 0.8 retornos por metro cuadrado, principalmente en áreas con pendientes pronunciadas donde un MDE de baja calidad es más sensible en la normalización de las alturas. Al respecto, Hansen Hofstad et al. (2015) observaron que a partir de una densidad mayor a 1 retorno por metro cuadrado los efectos sobre la generación del MDE no fueron significativos. Este estudio demostró que una densidad promedio de 1 retorno por metro cuadrado puede considerarse como valor óptimo para escaneos LIDAR posteriores en el SMIC.
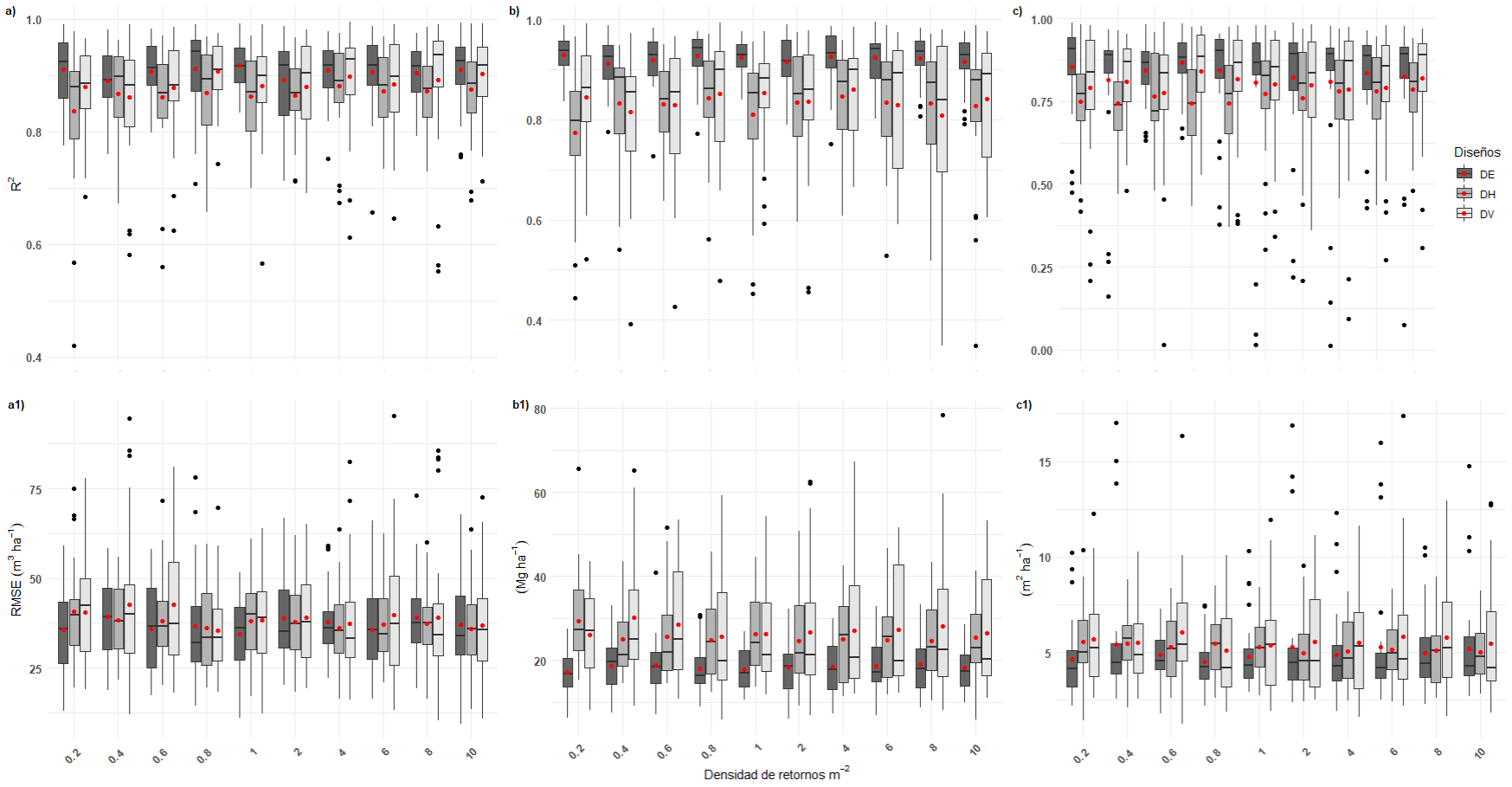
R2 y RMSE calculados mediante la validación cruzada repetida para; V (a-a1); B (b- b1) y AB (c-c1); los puntos negros representan puntos aberrantes.
FIGURA 3 Efecto de la densidad de retornos LIDAR en la modelización de área basal (AB), volumen (V) y biomasa (B) para los sitios muestreados bajo los diferentes diseños (n=96); DH (este-oeste), DV (norte-sur); DE (estratificado).
Las estimaciones de AB y V para los transectos del diseño DH fueron mapeados a nivel pixel con fines comparativos, mediante la aplicación de modelos GAM ajustados utilizando tres densidades de retornos: 0.8 m-2, 1 m-2 y 10 m-2 (Fig. 4). Se ejemplifica este diseño por considerarlo una manera de uso operativo actual de un sensor LIDAR, además de que presentó bondades de ajuste adecuadas. Las estimaciones a partir de 0.8 m-2 y 1 m-2 retornos (densidades bajas) se contrastaron con las estimaciones a partir de 10 m-2 (densidad alta) mediante la prueba estadística no paramétrica Mann-Whitney-Wilcoxon (Fig. 4), encontrándose que las estimaciones de AB fueron diferentes (P < 0.5), sin embargo, las estimaciones de V no fueron significativamente diferentes en términos de distribución y media (P > 0.5). Además, se encontró que las estimaciones derivadas de la densidad de 1 retorno por metro cuadrado fueron más conservadoras en comparación con las de 10 retornos por metro cuadrado.
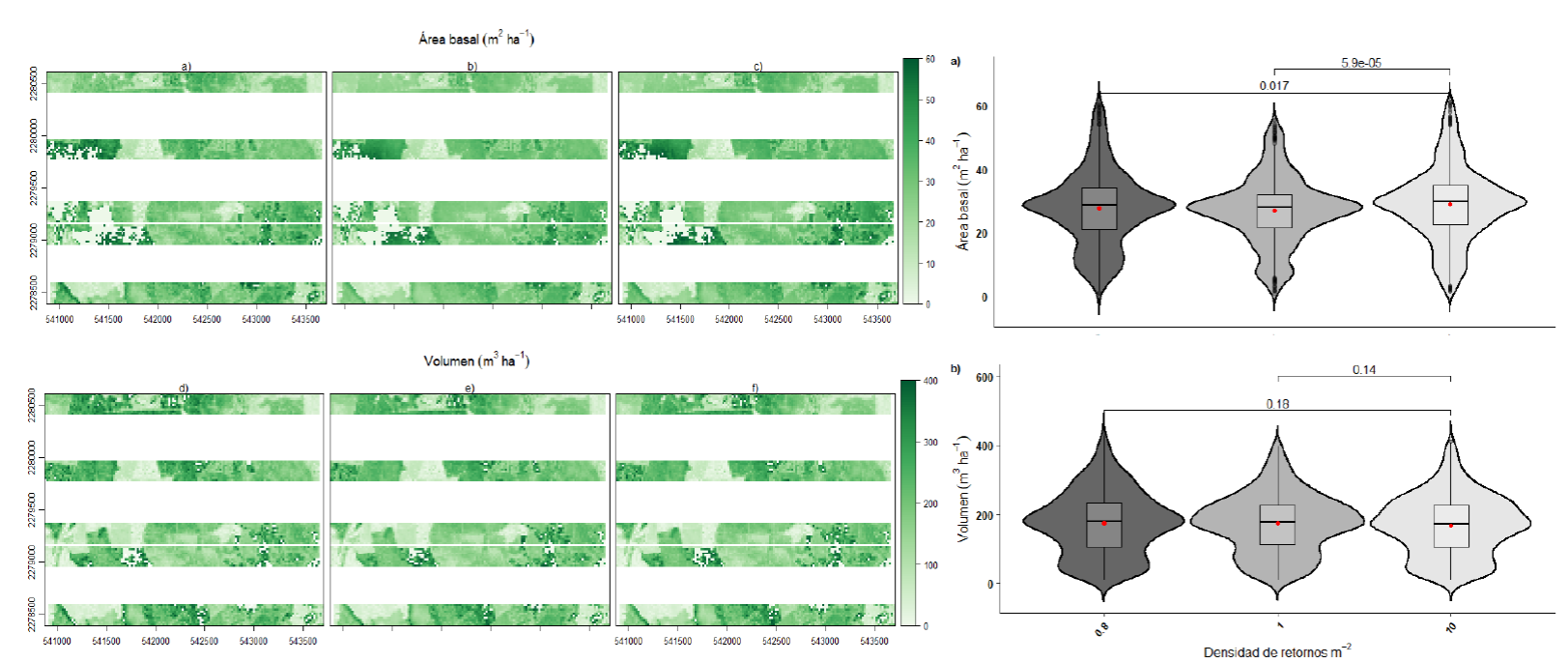
FIGURA 4 Estimacion de área basal y volumen en transectos este -oeste a partir de variables LIDAR calculados a densidades de retornos diferentes (izquierda). a y d) 0.8 pulsos por metro cuadrado; b y e) 1 pulso por metro cuadrado; c y f) 10 pulsos por metro cuadrado. Prueba Mann-Whitney-Wilcoxon (0.6-10 y 1-10) (derecha).
Las estimaciones de AB, V y B generadas para el área de los transectos a partir de un modelo GAM y una densidad de 1 retorno por metro cuadrado (considerado el más adecuado), sirvieron como variables de respuesta para ajustar otros modelos GAM y RF para estimar y mapear las mismas variables para todo el SMIC. Se utilizaron como predictores los valores de las bandas espectrales, el NDVI y métricas de textura derivadas del sensor RapidEye que registraron un coeficiente de correlación de Pearson alto con las variables de interés (AB, V y B): texturas construidas a partir de la banda roja (B3) (media y varianza), azul (media) (B1_mean), verde (media) (B2_mean) y el NDVI (media y varianza) (ventana móvil de 15 × 15) (Tabla 2). El modelo GAM presentó menor valor del porcentaje de varianza explicada (R2) y mayor RMSE en la estimación de AB, V y B, comparado con RF (Tabla 3). Sin embargo, todos los parámetros de suavizado que corresponden a las texturas del RGB y NDVI fueron altamente significativos (P < 0.0001).
TABLA 2 Variables (métricas) espectrales y de textura más correlacionadas (coeficiente de correlación -r) con las variables dasométricas.
| RapidEye | Variables dasométricas | ||
| Área basal (m2) | Volumen (m3) | Biomasa (Mg) | |
| B3_mean | -0.73 | -0.57 | -0.73 |
| B3_var | -0.72 | ||
| B1_mean | -0.72 | -0.55 | -0.72 |
| B2_mean | -0.70 | -0.53 | -0.69 |
| B3 | -0.69 | -0.54 | -0.69 |
| NDVI_var | 0.63 | 0.48 | 0.65 |
| NDVI_mean | 0.63 | 0.48 | 0.65 |
B1: banda azul, B2: verde, B3: rojo, B4: borde rojo, B5: infrarrojo, texturas (15 × 15) _mean y _var: media y varianza.
TABLA 3 Valores de bondad de ajuste de los modelos aditivos generalizados y el algoritmo random forest evaluados para estimar área basal, volumen total y biomasa aérea en el Sitio de Monitoreo Intensivo de Carbono.
| Modelo | Estructura del modelo | R2 | RMSE |
| GAM | AB=β0+ s(x,y)+s(B1_mean)+s(B2_mean)+s(B3_mean)+s(B3)+s(NDVI_mean)+s(NDVI_var) | 0.61 | 6.85 |
| RF | AB= s(x,y)+todas las métricas RapidEye | 0.73 | 5.69 |
| GAM | V= β0+s(x,y)+s(B1_mean)+s(B2_mean)+s(B3_mean)+s(B3)+s(NDVI_mean)+s(NDVI_var) | 0.61 | 54.15 |
| RF | V= s(x,y)+todas las métricas RapidEye | 0.71 | 46.95 |
| GAM | B= β0+s(x,y)+s(B1_mean)+s(B2_mean)+s(B3_mean)+s(B3)+s(NDVI_mean)+s(NDVI_var) | 0.67 | 29.24 |
| RF | B= s(x,y)+todas las métricas RapidEye | 0.79 | 23.67 |
A: área basal (m2), V: volumen (m3), B: biomasa aérea (Mg). B1: banda azul, B2: verde, B3: rojo, B4: borde rojo, B5: infrarrojo, NDVI: índice de vegetación normalizado, texturas (15 × 15) _mean y _var: media y varianza, β0 parámetro.
El modelo RF resultante incluyó cinco bandas del sensor Rapideye y 42 texturas, además de las coordenadas longitud (x) y latitud (y). Este algoritmo logró explicar las variables dasométricas de interés por arriba de 70%, teniendo mejor rendimiento en la estimación de la B (79%, RMSE = 23.67 Mg ha-1) seguido del AB (73%, RMSE = 5.69 m2 ha-1) y V (71%, RMSE = 46.95 m3 ha-1).
RF mostró mejores bondades de ajuste al utilizar texturas derivadas del sensor RapidEye, lo que coincide con lo observado en otros estudios (Matasci et al., 2018; Zhu et al., 2020). Una ventaja de RF es que implementa una validación cruzada a partir de conjuntos de datos de entrenamiento y validación para evitar la inflación de la varianza causada por el uso de variables redundantes en la explicación de la variable de interés (Fassnacht et al., 2014). Además, se ha observado una mejoría en las estimaciones con el uso de texturas usando el método GLCM, con un tamaño de ventana de 15 × 15 (Zhu et al., 2020) o mayor dependiendo la variabilidad del dosel. A diferencia de las métricas comunes, las métricas de textura espectral pueden reducir los impactos de sombra y extraer más eficazmente la información de bosques maduros, con ello pueden aumentar las correlaciones entre la textura y la masa forestal madura (Lu y Batistella, 2005), como en el caso del presente estudio.
Los mapas de AB y el V correspondientes al área boscosa del SMIC (815.03 ha) muestran que ambos modelos (GAM y RF) estiman con tendencia similar (Fig. 5). Los datos indican que el modelo GAM estimó valores totales de AB y V de menor magnitud que RF (Tabla 4), pero valores absolutos más altos en ambas variables (Fig. 6). Conforme a lo esperado, los valores más bajos de AB y V corresponden a rodales jóvenes, cosechados en 2003-2013 y los valores máximos corresponden a los rodales maduros y a áreas sin intervención silvícola (Tabla 5).
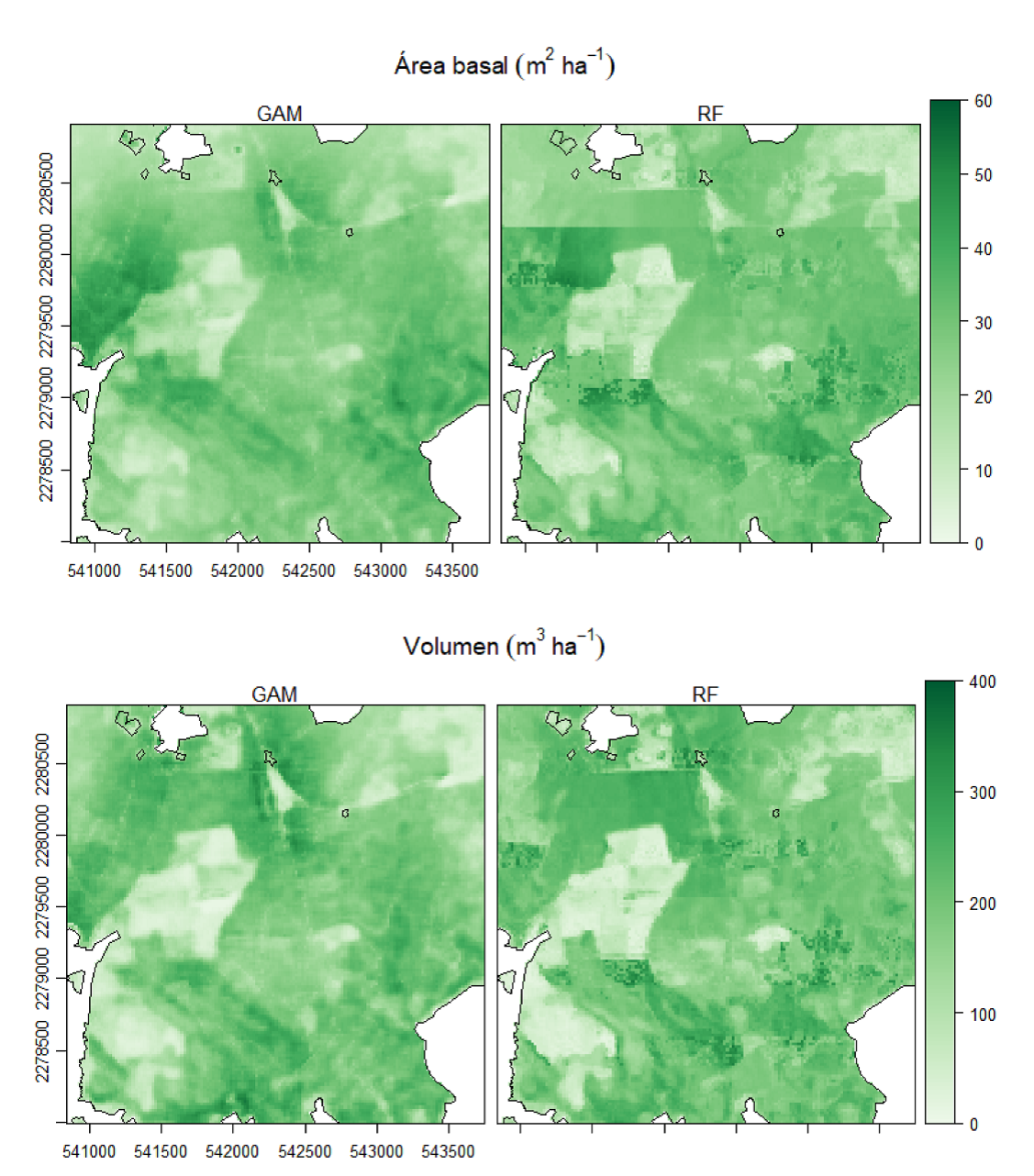
FIGURA 5 Variabilidad espacial del área basal y volumen de madera estimada a partir de modelos aditivos generalizados y el algoritmo random forest utilizando métricas derivadas del sensor RapidEye.
TABLA 4 Resumen de los valores de área basal y volumen total obtenidos mediante modelos aditivos generalizados y el algoritmo random forest en el Sitio de Monitoreo Intensivo de Carbono.
| Variable | N | Min | Max | Riq | Media | Sd | Inventario | |
| GAM | AB (m2 ha-1) | 20306 | 3.22 | 50.7 | 10.8 | 26.2 | 8.38 | 21 353.79 |
| Volumen (m3 ha-1) | 20306 | 7.39 | 468 | 86.3 | 173 | 64.9 | 141 000.19 | |
| RF | AB (m2 ha-1) | 20306 | 3.2 | 53.1 | 10 | 27 | 8.4 | 22005.81 |
| Volumen (m3 ha-1) | 20306 | 13.3 | 354 | 76.9 | 178 | 64.8 | 145075.34 |
AB: área basal, V: volumen total, N : total de sitios de 400 m2, Min: valor mínimo estimado, Max: valor máximo estimado, Riq: rango intercuantil, Sd: desviación estándar.
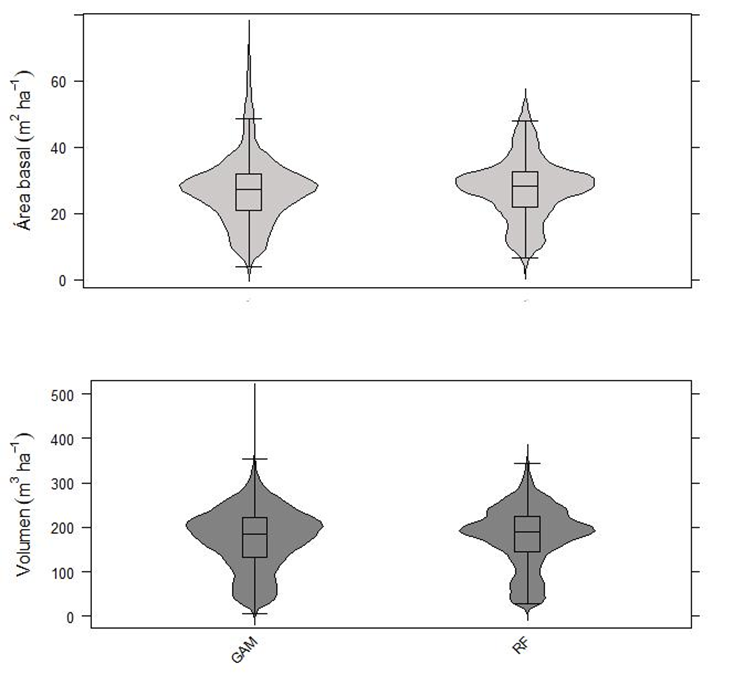
FIGURA 6 Diagrama de caja de las estimaciones de volumen de madera generadas a partir de modelos aditivos generalizados y el algoritmo random forest ajustados utilizando variables del sensor RapidEye.
TABLA 5 Estimador en dos etapas para la media e inventario total de área basal, volumen total y biomasa aérea obtenidos mediante los transectos estimados por modelos aditivos generalizados.
| Variable | Estrato | Media | SE | IC- | IC+ | Error % | Inventario | |
| AB (m2 ha-1) | Todos | 25.93 | 0.75 | 23.84 | 28.01 | 5.80% | 21 131.16 | |
| 1933 | 29.42 | 0.49 | 28.46 | 30.38 | 3% | 8 086.09 | ||
| 1982-1987 | 26.78 | 4.67 | 17.63 | 35.94 | 35% | 2 550.64 | ||
| 1988-1992 | 30.36 | 1.39 | 27.63 | 33.09 | 9% | 1 654.68 | ||
| 1993-1997 | 26.00 | 0.74 | 24.56 | 27.44 | 6% | 2 605.09 | ||
| 1998-2002 | 28.13 | 1.27 | 25.64 | 30.62 | 9% | 4 051.57 | ||
| 2003-2007 | 18.80 | 2.86 | 13.19 | 24.41 | 30% | 1 285.31 | ||
| 2008-2013 | 11.53 | 1.67 | 8.27 | 14.80 | 29% | 897.79 | ||
| Dos etapas | V (m3 ha-1) | Todos | 174.33 | 3.74 | 163.95 | 184.71 | 4.29% | 142 085.96 |
| 1933 | 213.75 | 3.10 | 207.68 | 219.82 | 3% | 58 753.79 | ||
| 1982-1987 | 210.37 | 10.53 | 189.73 | 231.02 | 10% | 20 034.79 | ||
| 1988-1992 | 228.85 | 7.08 | 214.97 | 242.73 | 6% | 12 473.40 | ||
| 1993-1997 | 170.86 | 5.10 | 160.87 | 180.85 | 6% | 17 119.52 | ||
| 1998-2002 | 165.70 | 10.37 | 145.37 | 186.03 | 13% | 23 865.76 | ||
| 2003-2007 | 80.82 | 8.80 | 63.58 | 98.07 | 22% | 5 525.10 | ||
| 2008-2013 | 55.42 | 7.50 | 40.73 | 70.11 | 27% | 4 313.62 | ||
| B (Mg ha-1) | Todos | 94.92 | 1.45 | 90.89 | 98.96 | 3.1% | 77 366.12 | |
| 1933 | 119.47 | 1.79 | 115.95 | 122.98 | 3% | 32 838.37 | ||
| 1982-1987 | 112.60 | 5.38 | 102.05 | 123.15 | 10% | 10 723.05 | ||
| 1988-1992 | 126.48 | 1.58 | 123.39 | 129.57 | 2% | 6 893.84 | ||
| 1993-1997 | 92.26 | 5.05 | 82.37 | 102.16 | 11% | 9 244.36 | ||
| 1998-2002 | 88.79 | 6.00 | 77.03 | 100.55 | 14% | 12 788.16 | ||
| 2003-2007 | 39.55 | 4.71 | 30.33 | 48.78 | 24% | 2 703.99 | ||
| 2008-2013 | 27.94 | 4.25 | 19.61 | 36.26 | 30% | 2 174.35 |
AB: área basal, V: volumen total, B: biomasa aérea, IC: intervalo de confianza a 95%.
La muestra de datos LIDAR (transectos) que representó 30% del total de la superficie del área de estudio, fue suficiente para estimar con precisión el AB, V y B, y para expandir las estimaciones a toda el área mediante la incorporación de datos espectrales RapidEye. Lo anterior sugiere que la estimación del tamaño óptimo de la muestra requiere de estudios más detallados al respecto. Chen y Hay (2011) observaron que una muestra de 8.8% (un solo transecto) de la superficie total aumentó el rendimiento (Volumen: R2= 0.64 y RMSE= 156.9 m3 ha-1) del algoritmo de aprendizaje utilizado [regresión de soporte de vectores (SVR Support Vector Regression)] para predecir variables de interés. Estos autores diseñaron cuatro muestras de transectos LIDAR (8.8%, 17.6%, 26.4% y 35.2% del área total) y las combinaron con imágenes QuickBird para estimar la altura del dosel, biomasa y volumen en Vancouver Island, Canadá. En otro estudio, Chen et al. (2012) evaluaron la proporción y dirección (Norte-Sur y Este-Oeste) de transectos LIDAR para estimar altura, biomasa y volumen en Quebec, Canadá y encontraron que un solo transecto que representó 7.6% del área total presentó mejores bondades de ajuste (volumen: R2 = 0.72; RMSE = 52.59 m3 ha-1) en el algoritmo SVR.
Estimadores de muestreo e inventario total
Estimador en dos fases
En la primera fase se seleccionó una muestra de 6457 pixeles (400 m2), dentro del diseño DH, que fue utilizada como variables auxiliares (LIDAR). La segunda fase incorporó los datos de campo derivados de la muestra de 96 sitios medidos. El estimador de la media en dos fases asistido por el modelo GAM mostró un error menor a 5% (Tabla 6). Estos resultados corroboran la utilidad de este tipo de modelos señalada por otros autores. De acuerdo con Massey (2015) el proceso de estimación a partir de información auxiliar (LIDAR) y datos de inventario en la segunda fase ofrece una reducción del sesgo debido a que el estimador presenta una muestra grande en la primera fase, en lugar del uso de información de pared a pared (área SMIC). Estudios previos como el de Kangas et al. (2016) han utilizado el muestreo en dos fases asistido por un modelo GAM, demostrando cómo las técnicas de estimación no paramétricas incorporan resultados prometedores incluso en el caso de los modelos complejos (GAM) y diseños multifásicos.
TABLA 6 Estimador por regresión en dos fases para la media e inventario total de área basal, volumen total y biomasa aérea obtenidos mediante los transectos estimados por modelos aditivos generalizados.
| Estimador | Variable | n1:n2 | Media | Se ext | IC- | IC+ | Error % | Inventario |
| AB (m2 ha-1) | 26.61 | 0.45 | 25.73 | 27.50 | 3.33% | 21 689.52 | ||
| Dos fases | V (m3 ha-1) | 6 457:96 | 164.82 | 4.21 | 156.47 | 173.17 | 5.07% | 134 333.05 |
| B (Mg ha-1) | 91.12 | 2.15 | 86.84 | 95.40 | 4.69% | 74 268.59 |
AB: área basal, V: volumen total, B: biomasa aérea, n1 y n2: tamaño de muestra en la primera y segunda fase, IC: intervalo de confianza a 95%.
Estimador en dos etapas
En este método los transectos LIDAR que contienen las estimaciones realizadas con el modelo GAM fueron consideradas como UMP y cada una de las celdas de 400 m2 como UMS. Para cada UMP se asumió a las clases de edad como estratos para estimar una media general y por estrato con base en la ponderación (Gregoire et al., 2011).
Los resultados indican que el error estimado es bajo (4.29% para el volumen) y aumenta en los rodales más jóvenes o recién aprovechados (Tabla 5); esto se debe a que dentro de las UMP se encuentran menor número de celdas clasificadas para esas clases (Gregoire et al., 2011). Análisis previos para la misma área mencionan un error mayor para las áreas sin intervención silvícola argumentando que se establecieron pocos sitios en campo en ese estrato, lo que implica una mayor variación en la estimación de la media (Ortiz-Reyes et al., 2015; Torres-Vivar et al., 2017).
Conclusiones
Los modelos GAM ajustados bajo tres diseños de muestreo para inventario forestal asistido por datos de un sensor LIDAR aerotransportado permitió identificar al diseño estratificado (DE) como el mejor (RMSE: V = 37.01 m3 ha-1, B = 18.26 Mg ha-1 y AB= 4.97 m2 ha-1), aun en densidades de retornos bajas. Aunque este diseño de muestreo no se utilizó para la estimación del inventario total del SMIC, los resultados alientan la posibilidad de su aplicación en inventarios forestales operativos mediante la captura de datos LIDAR a través de sensores montados en drones.
Se encontró que una densidad de datos LIDAR de 1 retorno por metro cuadrado fue suficiente para obtener estimaciones precisas de AB, V y B en bosques templados bajo manejo coetáneo, lo que permitirá considerar en futuros planes de vuelo para colecta de datos LIDAR una mayor altura de vuelo, con la consecuente reducción de tiempo y costo de escaneo. Los modelos de regresión GAM y al algoritmo Random Forest demostraron propiedades importantes en la estimación de las variables de interés forestal tanto a escala de transectos como en áreas donde la información LIDAR no está presente, pero se cuenta con otro tipo de imágenes ópticas de resolución espacial fina.
Los estimadores de muestreo en dos fases y en dos etapas demostraron ser estimadores compatibles con las características de vuelo LIDAR mediante transectos, permitiendo alcanzar precisiones de muestreo menores o iguales a 6%.











 nueva página del texto (beta)
nueva página del texto (beta)




