Introduction
After 17 years of coining “Genomic Selection (GS)” it has been possible to accelerate the processes of plant breeding by reducing the cycles to obtain a new variety using the information from genetic markers, since genetic markers have become more economical and accessible. Although GS has become popular in plant and animal breeding programs, in order to improve this methodology, the predictive accuracy of GS models needs to be improved, because GS trains predictive models using phenotypic and genotypic information of the training sample and makes predictions for the validation sample (with only genomic information) using these models.
GS prediction tools are mostly Bayesian models, because they have demonstrated good predictive performance and are able to function well under the context where there are more independent variables (markers) than observations. However, these models are generally very demanding in terms of execution time, also the different variations of Bayesian methods, such as Bayes A, Bayes B, Bayes Ridge Regression, etc., do not provide a great improvement in prediction accuracy (Mota et al., 2018). Therefore, there are consensus of the need for more efficient predictive models for the genomic selection, since the quantity of data collected (genotypic and genotypic) in breeding programs continues to increase, and we want to extract useful knowledge from these data to improve the selection process of plants and animals.
For this reason, Montesinos-López et al. (2018) proposed the use of the Item Based Collaborative Filtering (IBCF) methodology for the context of GS, invention attributed to Amazon No. US6266649B1 (2001); this methodology has become fundamental to improve the performance of electronic commerce, and has been used efficiently in sites such as Amazon, where it is used for the recommendation of books and other products for sale, as well as in various web-sites dedicated to products sale, to recommend users similar products (Wei et al., 2012).
This methodology provides several advantages, one is its simplicity compared to Bayesian models, another, the computational efficiency, even in the processing of large amounts of data. However, its successful performance depends strongly on the amount of correlation between traits or environments. Since, the genetic variability between plants of the same species is low in comparison to other taxonomic kingdoms like animalia, we can expect high correlation rates between individuals, allowing in theory a good performance of IBCF. The implementation of this methodology is based in the calculation of a matrix of relationships or similarity matrix between traits (or environments) and there are different ways to calculate this matrix (Wei et al., 2012), as the Pearson’s correlation, cosine similarity among others.
It is important to point out, that there is an R package for implementing this methodology to the GS context called IBCF.MTME (Montesinos-López et al., 2018). This package allows users to implement the IBCF algorithm to data sets commonly found in GS that has multi-environment, multi-trait and simultaneous multi-trait and multi-environment data sets.
For this reason, this research carried out a comparative study between IBCF and Genomic Best Linear Unbiased Prediction (GBLUP) model. We performed prediction accuracy between the two models using six real data sets from maize and wheat, using cross validation.
Materials and methods
Statistical models
(Equation 1) is the model used
under the GBLUP model. Where represents the normal response observed in the -th
line in the j-th environment, where
Note that E
i
represents the j-th environment, G
represents the genomic effect of the j-th line and is assumed
as a random effect distributed as
On the other hand, to make the prediction of all traits simultaneously we propose the model given in equation (2),
Where y
ijk
is the response variable in the i-th environment,
j-th line and k-th trait,
ET
ik
represents an interaction between the i-th environment
and k-th trait, GT
jk
represents an interaction between the genomic effect of the
j-th line and the k-th trait and is
assumed as a random effect
Item based collaborative filtering (IBCF)
The IBCF algorithm is very popular with electronic-commerce web sites for
recommending items and products, where they use inputs about a customer’s
interests to generate a list of recommended items. This algorithm was recently
implemented in genomic selection and proved to be comparable to conventional
whole- genome prediction models when the correlation between traits and
environments was moderate or high (Montesinos-López et al., 2018). The IBCF algorithm
works by building a database of users’ (lines) preferences for items
(trait-environment combination). For example, Table 1a provides raw phenotypic data with six lines evaluated in
two different environments (E1 and E2) for two different traits (T1 and T2) with
both traits in different scales, also this raw phenotypic data set has 4 missing
values (with NA). Then we standardize by column ([
Table 1 Example of item based collaborative filtering (IBCF). (a) Raw phenotypic data, (b)
Standardized phenotypic data and (c) matrix of correlation of
standardized phenotypic data. Line denotes lines, T1 denotes traits
1, while E1, E2, E3 and E4 environments 1, 2, 3 and 4 respectively.
Tabla 1. Ejemplo de filtrado colaborativo (IBCF). (a)
Datos fenotípicos sin procesar, (b) Datos fenotípicos estandarizados
y (c) matriz de correlación de datos fenotípicos estandarizados.
Line denota líneas, T1 denota rasgo 1, mientras que E1, E2, E3 y E4,
ambientes 1, 2, 3 y 4 respectivamente.
| Raw phenotipic data (a) | ||||
|---|---|---|---|---|
| Line | T1_E1 | T1_E2 | T1_E3 | T1_E4 |
| Line1 | 13.43869 | 10.042283 | 7.833255 | 3.346331 |
| Line2 | NA | 10.206126 | 7.539531 | 4.009220 |
| Line3 | 15.98278 | 10.758225 | 8.103404 | NA |
| Line4 | 13.28755 | NA | 7.508226 | 2.305872 |
| Line5 | 15.12665 | 10.625251 | 4.835037 | |
| Standardized phenotipic data (b) | ||||
| Line | T1_E1 | T1_E2 | T1_E3 | T1_E4 |
| Line1 | -0.7763412 | -1.0793621 | 0.3117081 | -0.2598054 |
| Line2 | NA | -0.5957629 | -0.7388356 | 0.3601804 |
| Line3 | 1.1595774 | 1.0338048 | 1.2779277 | NA |
| Line4 | -0.8913464 | NA | -0.8508002 | -1.2329245 |
| Line5 | 0.5081103 | 0.6413202 | NA | 1.1325495 |
| Matrix of correlation (c) | ||||
| Line | T1_E1 | T1_E2 | T1_E3 | T1_E4 |
| T1_E1 | 1.000 | 0.9869829 | 0.8643881 | 0.9402111 |
| T1_E2 | 0.9869829 | 1.0000000 | 0.7193678 | 0.9830228 |
| T2_E1 | 0.8643881 | 0.7193678 | 1.0000000 | 0.2130462 |
| T2_E2 | 0.9402111 | 0.9830228 | 0.2130462 | 1.0000000 |
Where
Next, we illustrate how to calculate the four missing values using formula (1). First, we calculate the scaled predicted value for y 21
Then the predicted value of y21 in its original scale is equal to
This mean that the predicted value of line 2 in trait-environment combination 1(
Then the predicted value of y 34 in its original scale is equal to
Now the predicted value of line 3 in trait-environment combination 4 (
Then the predicted value of y 42 in its original scale is equal to
This mean that the predicted value of line 4 in trait-environment combination 2 (
Then the predicted value of y 53 in its original scale is equal to
This mean that the predicted value of line 5 in trait-environment combination 3 (
As we can see with this example the calculations are easy but laborious, but the
IBCF.MTME packages do this job automatically and the data set required can be on
different scales (not standardized) for the traits, that is, the traits are
allows to be measured on different scales. Internally, the IBCF. MTME package
standardize ([
Table 2 Execution time in seconds, of the GBLUP and IBCF method. Ratio was obtained as the
division of the time in seconds required by the GBLUP model and the
time required under the IBCF method.
Tabla 2. Tiempo de ejecución en segundos, del método
GBLUP e IBCF. La relación (ratio) se obtuvo como la división del
tiempo en segundos requerida por el modelo GBLUP y el tiempo
requerido por el método IBCF.
| Dataset | GBLUP | IBCF | Ratio |
|---|---|---|---|
| Maize | 35.48 | 2.5 | 14.19 |
| Maize_HEL | 21.23 | 0.79 | 26.87 |
| Maize_USP | 275.58 | 2.95 | 93.42 |
| Wheat_BGLR | 197.82 | 0.66 | 299.73 |
| Wheat_IBCF | 34.28 | 1.03 | 33.28 |
| Wheat_Iranian | 1152.36 | 2.19 | 526.19 |
| Mean | 286.12 | 1.68 | 169.63 |
Evaluation of the prediction accuracy
Two cross-validation schemes were used to assess the prediction accuracy of both models. Both schemes simulate two key situations that breeders often witness. The first corresponds to a cross validation with 10 random partitions, which simulates situations where some lines have been evaluated in some environments but in others are lost. The percentage of missing values correspond to 20% of the lines of each data set, in other words, 80% of the observations in the data sets have been used to train the models.
The second scheme simulates a situation with a non-evaluable trait in all the lines in an environment, but is present in the remaining environments. In this case, information from known data in other environments is used, and the evaluation of the prediction can benefit from the loan of information between lines across environments, and between correlated traits. From the variety of methods used to compare the predictive ability, we used Pearson´s correlation and we report the average of the 10 random partitions. Models with a higher correlation indicate better predictions.
Statistical software
The statistical software R version 3.5.0 (R Core Team, 2018), was used using the external packages IBCF.MTME version 1.2-5 and the GFR package which includes different tools that provide some points for prediction models implementation in the GS context, this package was used in version 0.9-12 (Montesinos-López et al., 2018).
Real data sets
This research analyzed six different real datasets obtained from various studies, the data are available in the following link, below is a description of the content of each data set.
Maize dataset
This data set is based on that of Montesinos-López et al. (2017). It is composed of a sample of 309 maize lines evaluated for three traits: anthesis-silking interval (ASI), plant height (PH), grain yield (GY), each of them evaluated in three optimal storm environments (Env1, Env2 and Env3). The total number of genomes by sequencing (GBS) data were 681,257 single nucleotide polymorphisms (SNPs), and, after filtering for missing values and minor allele frequency, were used 158,281 SNPs for the analyses. We have identified this data set as Maize. For more details, see the study of Montesinos-López et al. (2017).
Maize Hel dataset
This data set is based on the data used in the study of Cuevas et al. (2018). It consists of a sample of 247 maize lines evaluated in 2015 in three environments corresponding to Nova Mutum (NM) in the state of Mato Grosso, Pato de Minas (PM) and Ipiaçú (IP) in the state of Minas Gerais, Brazil. The traits evaluated were: Ear height (EH), PH and GY. The HEL parent lines were genotyped with an Affymetrix Axiom Maize Genotyping Array of 616 K SNPs with standard quality controls removing markers with a Call Rate 0.95. This data set differs from the cited study is the elimination of unmeasured maize lines in one of the traits, as well as two environments where the three traits had not been measured in an effort to have a balanced data set, in the same way they were removed from the genomic matrix. We have identified this data set as Maize_HEL. For more details, see the study of Cuevas et al. (2018).
Maize USP dataset
This data set is based on the data used in the study of Cuevas et al. (2018). It consists of 720 lines of corn evaluated in Piracicaba and Anhumas, Brazil, each with two levels of nitrogen fertilization (N): Ideal N (IN) and Low N (LN) for a total of four artificial environments (PIN, PLN, AIN and ALN), for three traits (EH, PH, GY). Like the data set Maize_HEL, the Maize_USP parent lines were genotyped with an Affymetrix Axiom Maize Genotyping Array of 616 K SNPs with standard quality controls removing markers with a Call Rate 0.95 in addition. Like the above data set, it differs from the data from the cited study in the removal of lines that did not contain all its complete measurements to have a balanced data set. We have identified this data set as Maize_USP. For more details, see the study of Cuevas et al. (2018).
Wheat BGLR dataset
This data set is based on the data used in the study of Crossa et al. (2010) and it is preloaded in the BGLR package. It consists of 599 wheat lines evaluated in four different environments. The 599 wheat lines were genotyped using 1447 Diversity Array Technology (DArT) markers. The markers with a minor allele frequency (MAF) (0.05) were removed, and missing genotypes were imputed using samples from the marginal distribution of marker genotypes. The number of DArT markers after edition was 1279. We have identified this data set as Wheat_BGLR. For more details, see the study of Crossa et al. (2010).
Wheat IBCF dataset
This data set is based on the data used in the study of Montesinos-López et al. (2016) a multi-environment single trait model for assessing genotype \u00d7 environment interaction (G \u00d7 E and it is preloaded in the IBCF.MTME package. It consists of a sample of 250 lines of wheat grown during the 2013-2014 harvest season in Ciudad Obregon, Sonora, Mexico. The trials were planted in mid-November and grown in beds with 5 and 2 irrigations plus drip irrigation. Four traits were recorded: (1) Days to heading (DT) which corresponds to the number of days from germination until 50% of the peaks in each plot appeared, (2) GY corresponding to the total grain yield of the plot after maturity, (3) PH recorded in centimeters, and (4) the vegetative index (NDVI) was calculated from the data collected through a hyperspectral chamber. Genotyping-by-sequencing was used for genome-wide genotyping. Single nucleotide polymorphisms were called across all lines using the TASSEL GBS pipeline anchored to the genome assembly of Chinese Spring. Single nucleotide polymorphism calls were extracted, and markers filtered so that percent missing data did not exceed 80% and 20%, respectively. Individuals with 80% of missing marker data were removed, and markers were recorded as 2, 0, and 1, indicating homozygous for the minor allele, heterozygous, and homozygous for the major allele, respectively. Next, markers with 0.01 minor allele frequency were removed, and missing data imputed with the marker mean. A total of 12,083 markers remained after marker editing. We have identified this data set as Wheat_IBCF. For more details, see the study of Montesinos-López et al. (2016) a multi-environment single trait model for assessing genotype \u00d7 environment interaction.
Wheat Iranian dataset
This data set is based on the data used in the study of Crossa et al. (2016). It consists of 2374 wheat lines that were evaluated in field (D) and heat (H) drought experiments at the CIMMYT experimental station near Ciudad Obregón, Sonora, Mexico (27°20′ N, 109°54′ W, 38 meters above sea level), during the Obregón 2010-2011 cycle. Two traits were evaluated (DTM days at maturity and DTH days to heading). From a total of 40,000 markers, after quality control 39,758 markers were used. We have identified this data set as Wheat_Iranian. For more details, see the study of (Crossa et al., 2016).
Results
The results are discussed in seven sections, one for each data set. Each section has three subsections, the first one explains the prediction accuracy under the first type of cross validation (CV1), the second the predictions resulting of the second cross validation and the third provide a comparison in terms of time of implementation between the IBCF and the GBLUP model.
Maize dataset
Figure 1 shows two types of predictions using the two implemented models GBLUP and IBCF. First, the predictions are presented using the breeding values (phenotypic values adjusted using the markers) and these are the values that will be predicted. In the second case, the goal is to predict the phenotypic values. Under the GBLUP model, two models are fitted with genomic information and without the genomic information.
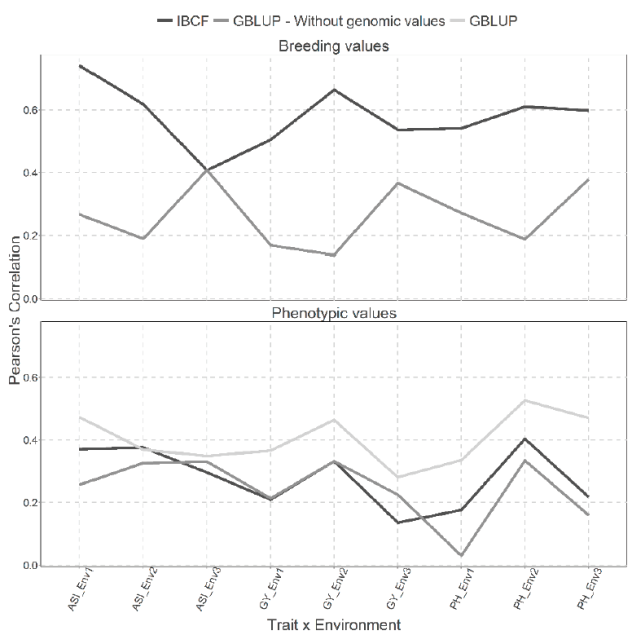
Figure 1 Prediction accuracy of CV1 obtained with Pearson´s correlation for both models IBCF
and GBLUP, using phenotypic values and breeding values as the
response variable for the Maize data set. The results of average
Pearson´s correlation correspond to the testing set of a cross
validation with 10 random partitions with 80% for training and 20%
for testing
Figura 1. Capacidad predictiva de CV1 obtenida con la
correlación de Pearson para ambos modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos de Maize. Los resultados de la correlación
promedio de Pearson corresponden al conjunto de prueba de una
validación cruzada con 10 particiones aleatorias con 80% para
entrenamiento y 20% para prueba.
The best predictions are observed under the scenario for breeding values compared with that for phenotypic values, which is to be expected, since it eliminates the uncertainty by the adjustment to the phenotypic values by the markers to obtain the breeding values. When breeding values are predicted, it is observed that the best predictions in most of the trait-environment combinations have been obtained through the IBCF model, because when comparing these results with the GBLUP model, differences can be appreciated in most cases (8 out of 9 trait-environment combinations). Only in the trait-environment ASI-Env3 is similar between the predictive capabilities of both models, the rest of the combinations IBCF model is superior to GBLUP (Figure 1).
On the other hand, when using phenotypic values, we can observe similar results between IBCF and GBLUP without the genetic values. The GBLUP obtains significantly lower predictive capacities only in two points and these correspond to the ASI and PH traits for environment 1. When comparing the GBLUP with genetic values versus the IBCF, we found that 7 out of 9 trait-environment combinations are different and GBLUP shows better prediction accuracy (Figure 1).
Figure 2 show the same two types of cross-validation given in Figure 1. However, now the predictions were made for all lines of one environment for each trait, using the remaining data as training data (CV2).
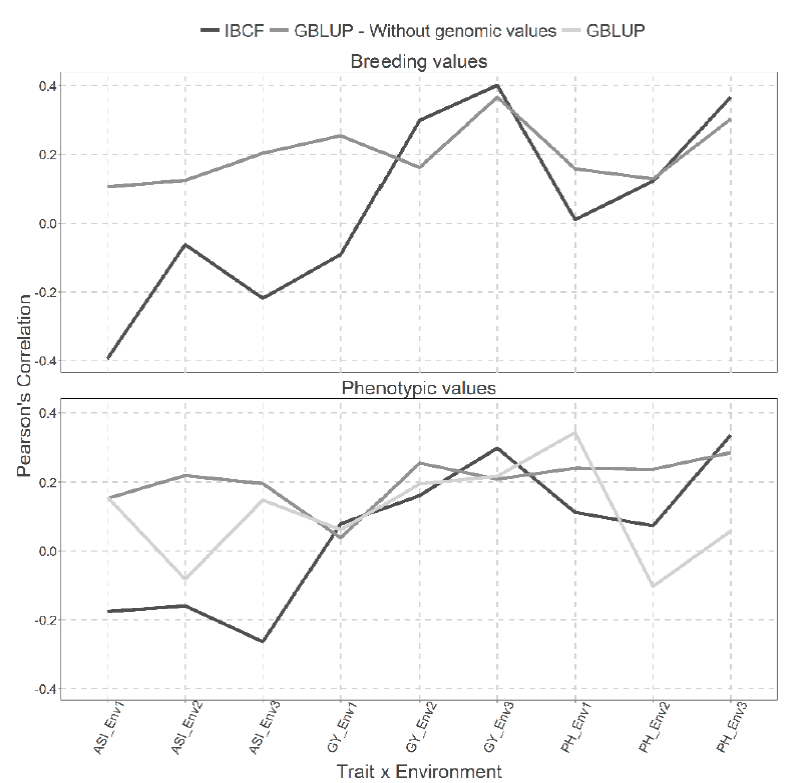
Figure 2 Predictive accuracy of CV2 obtained with Pearson´s correlation for the two models IBCF
and GBLUP, using phenotypic values and breeding values as the
response variable for the Maize data set. Pearson´s correlation are
reported for each trait-environment combination
Figura
2. Capacidad predictiva de CV2 obtenida con la
correlación de Pearson para los dos modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores geneticos como variable de respuesta
para el conjunto de datos de Maize. La correlación de Pearson se
informa para cada combinación de rasgo-ambiente.
When predicting breeding values, the GBLUP model proved to be superior. In ASI trait in all environments, we obtained the best predictions under the GBLUP model. While in GY trait, the best predictions were observed only in the first environment, while in the remaining environments the best predictions were observed under the IBCF model (Figure 2).
On the other hand, using phenotypic values, we observe that using the GBLUP model without genetic values results in better predictions for the ASI trait in the three environments and for the PH trait in environments 2. While including the genetic values gives better predictions only for PH trait in environment 1 (Figure 2).
Finally, we compared the runtimes of GBLUP vs. IBCF for Maize data using the breeding values and found that the GBLUP takes 35.48 seconds to implement while the IBCF takes only 2.5 seconds, which means that the IBCF is 14.19 times faster than the GBLUP model (Table 2).
Maize HEL dataset
Figure 3 show two types of predictions for both type of models under CV1 cross validation, the first for predicting the breeding values and the second for predicting the phenotypic values. We cannot observe gain between the scenarios where breeding values have been predicted against the scenarios where phenotypic values were predicted for the Maize_HEL data set. When the breeding values were predicted the results obtained are quite similar (2 of 9 combinations are different) under both models, with the exception for the GY trait in the IP and PM environments, where the best predictions accuracies were obtained by the IBCF model (Figure 3).
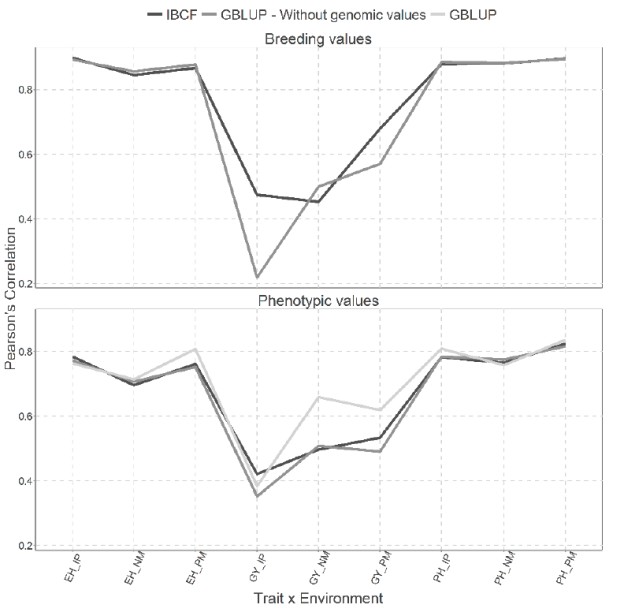
Figure 3 Prediction accuracy under CV1 with Pearson´s correlation for models IBCF and GBLUP,
using phenotypic values and breeding values as the response variable
for the Maize_HEL data set. The results of average Pearson
correlation correspond to a cross validation with 10 partitions with
80 % for training and 20% of testing.
Figura 3. Capacidad predictiva bajo CV1 con la
correlación de Pearson para los modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos Maize_HEL. Los resultados de la correlación
promedio de Pearson corresponden a una validación cruzada con 10
particiones con 80% para entrenamiento y 20% de prueba.
We can observe for the analysis performed using the phenotypic values, that the results obtained with the GBLUP model with (and without) the genomic values are similar to the results obtained with the IBCF model (only 1 out of 9 combination is different) this difference was obtained for the GY trait in the NM environment (Figure 3).
Figure 4 also give the same two types of predictions than in Figure 3, but implemented with the CV2 cross validation. Better predictions were obtained under the scenario where breeding values were predicted than under the scenario where phenotypic values were predicted. When breeding values were predicted, small differences were observed between both models, except in the trait-environment combination that corresponds to the GY trait in the IP environment where the best predictions were under the IBCF model. On the other hand, for the three trait-environment combinations that correspond to the PH the best predictions were observed with the GBLUP model (Figure 4).
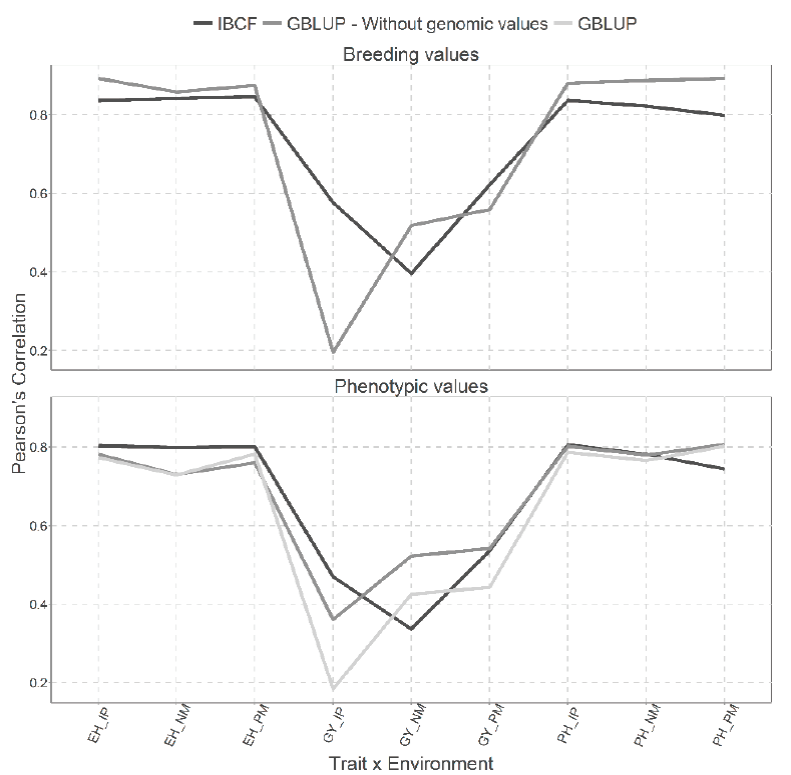
Figure 4 Prediction accuracy under CV2 with Pearson´s correlation for two models IBCF and
GBLUP, using phenotypic values and breeding values as the response
variable for the Maize_HEL data set. Pearson´s correlation results
correspond to each trait-environment combination
Figura 4. Capacidad predictiva bajo CV2 con la
correlación de Pearson para dos modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos Maize_HEL. Los resultados de la correlación
de
When the phenotypic values were predicted, the results obtained with the GBLUP model without using the genotypic values are similar to those obtained with the IBCF model, although in the trait-environment combination GY-NM, lower predictions were obtained with the IBCF model. Finally, with the GBLUP model with genomic information we observed low predictions for the GY trait for the environments IP and PM (Figure 4).
Finally, we compared the runtimes of GBLUP versus IBCF for the Maize_HEL data set using the breeding values and we found that the GBLUP takes 31.23 seconds to implement while the IBCF takes only 0.79 seconds, which means
Figure 6, as Figure 5, also shows two types of predictions with breeding values and phenotypic values, but with the cross validation, CV2. We obtained better predictions under the scenario predicting breeding values, than under the scenario where phenotypic values are predicted. When predicting breeding values, we observed the best predictions under the GBLUP model for all the trait-environment combinations.
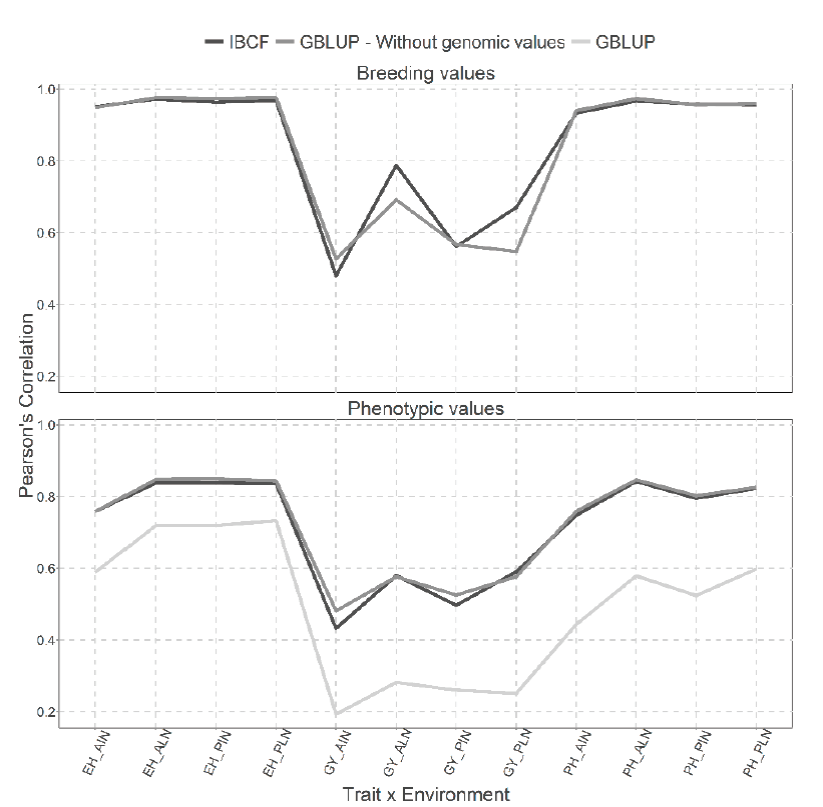
Figure 5 Prediction accuracy under CV1 with Pearson´s correlation for models IBCF and GBLUP,
using phenotypic values and breeding values as the response variable
for the Maize_USP data set. The results of average Pearson´s
correlation correspond to a cross validation with 10 partitions with
80 % for training and 20% of testing
Figura 5. Capacidad predictiva bajo CV1 con la
correlación de Pearson para los modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos Maize_USP. Los resultados de la correlación
promedio de Pearson corresponden a una validación cruzada con 10
particiones con 80% para entrenamiento y 20% de prueba
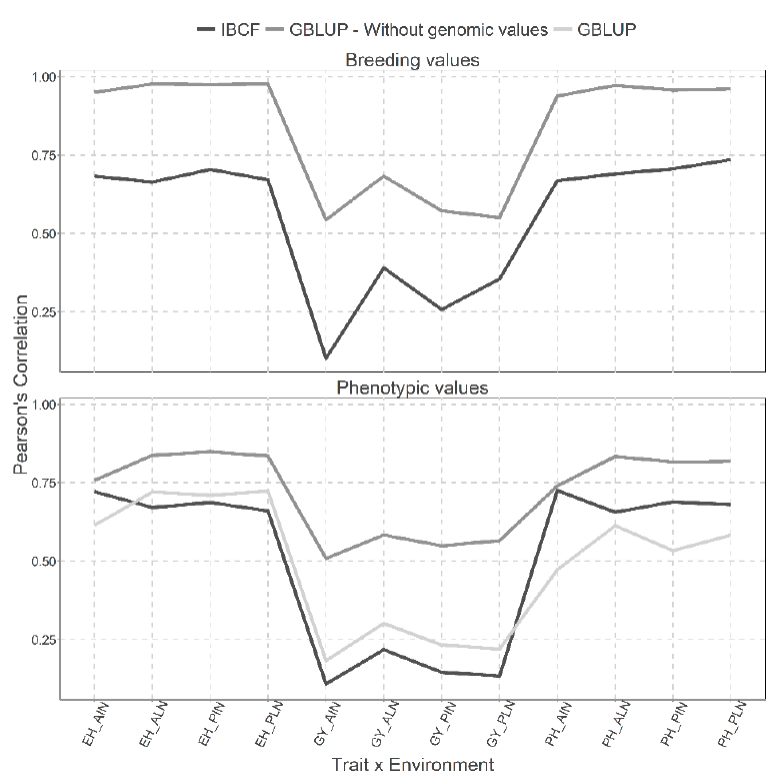
Figure 6 Prediction accuracy under CV2 with Pearson´s correlation for two models IBCF and
GBLUP, using phenotypic values and breeding values as the response
variable for the Maize_USP data set. Pearson´s correlation results
correspond to each trait-environment combination.
Figura 6. Capacidad predictiva bajo CV2 con la
correlación de Pearson para dos modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos Maize_USP. Los resultados de la correlación de
Pearson corresponden a cada combinación de rasgo-ambiente.
On the other hand, for the results predicting the phenotypic values, we observe similar results with the IBCF and GBLUP models that takes into account the genomic values, except in some points where the IBCF had deficiencies. These correspond to the GY trait for all the environments, as well as some points where it has obtained better predictive capacities; these correspond to the PH trait for all the environments. However, when the genomic values were removed from the GBLUP model, was the best for all the trait-environment combinations.
Finally, we compared the runtimes of GBLUP versus IBCF for the Maize_USP data set with breeding values and we found that the GBLUP takes 275.58 seconds to implement while the IBCF takes only 2.95 seconds, which is equivalent to the IBCF being 93.42 times faster than the GBLUP model (Table 2).
Maize USP dataset
Figure 5 presents under CV1 cross validation, two types of predictions for both type of models, the first for predicting the breeding values and the second for predicting the phenotypic values. We can observe a gain in the scenario where breeding values have been predicted against the scenarios where phenotypic values were predicted for the Maize_USP data set. When the breeding values were predicted, the results obtained are quite similar (9 of 12 combinations are similar) and of those different two of them favor the IBCF model and one the GBLUP model (Figure 5). While for the analysis performed using the phenotypic values, it is evident that the results obtained with the IBCF and GBLUP model without the genomic values are better to the results obtained with GBLUP model with the genomic values. However, the GBLUP model without the genomic values are similar to the results obtained with the IBCF model (Figure 5).
Wheat BGLR dataset
Figure 7 shows two types of predictions for both type of models, under CV1 cross validation. The best predictions were under the scenario that predicts the breeding values compared with the scenario that predicts the phenotypic values for the Wheat_BGLR data set. When the breeding values were predicted, it is observed that the IBCF was better in 3 out of 4 combinations than the GBLUP (Figure 7). On the other hand, when using the phenotypic values, it is evident that the GBLUP model without genomic information is quite similar to the IBCF model. While the for the GBLUP model with the genomic information produced the lower predictions (Figure 7)
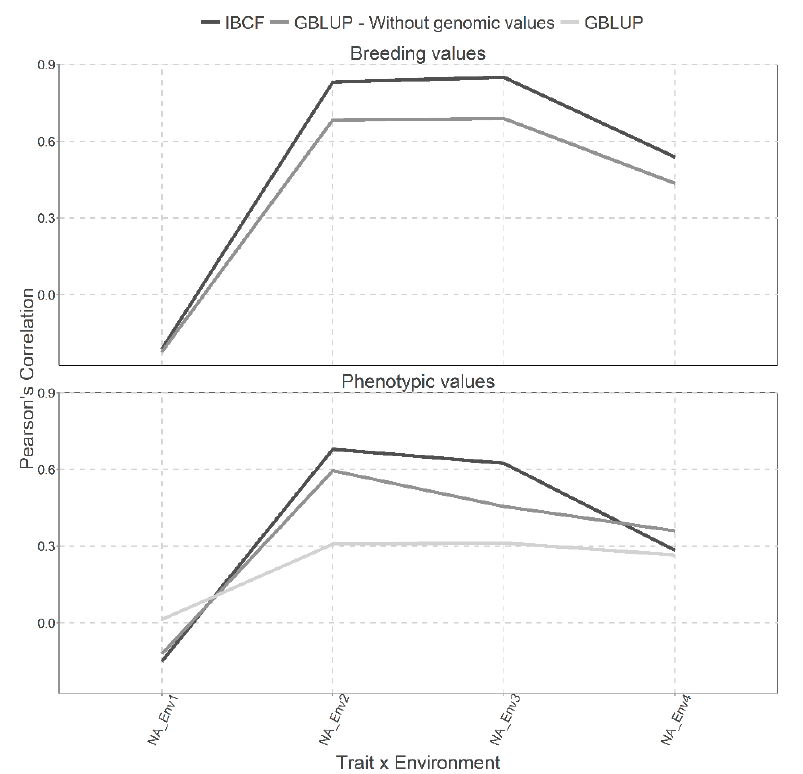
Figure 7 Prediction accuracy under CV1 with Pearson´s correlation for models IBCF and GBLUP,
using phenotypic values and breeding values as the response variable
for the Wheat_BGLR data set. The results of average Pearson
correlation correspond to a cross validation with 10 partitions with
80 % for training and 20% of testing.
Figura 7. Capacidad predictiva bajo CV1 con la
correlación de Pearson para los modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos Wheat_BGLR. Los resultados de la correlación
promedio de Pearson corresponden a una validación cruzada con 10
particiones con 80% para entrenamiento y 20% de prueba.
Finally, we compared the runtimes for the GBLUP versus the IBCF for the Wheat_BGLR data using the breeding values and we found that the GBLUP takes 197.82 seconds to implement, while the IBCF takes only 0.66 seconds, which means that the IBCF is 299.73 times faster than the GBLUP model (Table 2).
Wheat IBCF dataset
Figure 8 presents two types of predictions for both type of models, the first for predicting the breeding values and the second for predicting the phenotypic values. For these cases, CV1 cross validation has been used.
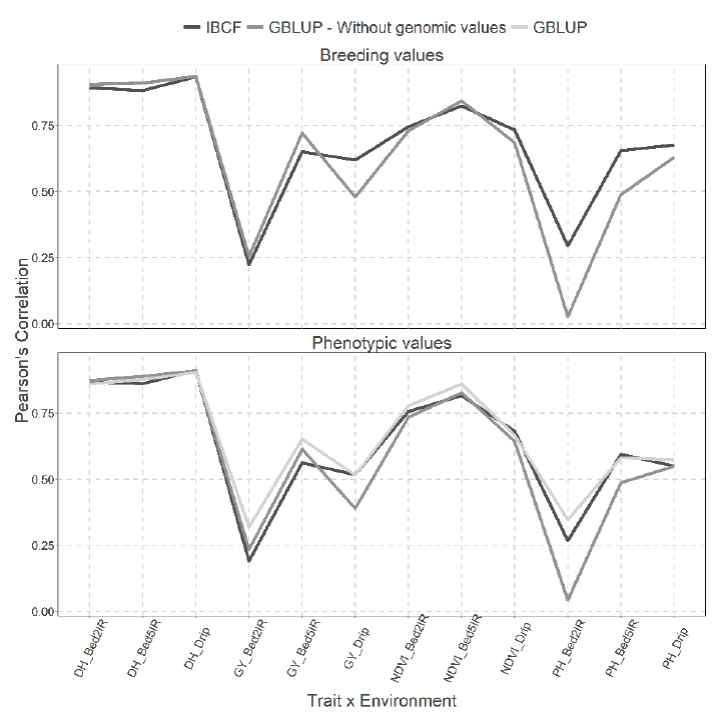
Figure 8 Prediction accuracy under CV1 with Pearson´s correlation for models IBCF and GBLUP,
using phenotypic values and breeding values as the response variable
for the Wheat_IBCF data set. The results of average Pearson´s
correlation correspond to a cross validation with 10 partitions with
80 % for training and 20% of testing
Figura 8. Capacidad predictiva bajo CV1 con la
correlación de Pearson para los modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos Wheat_IBCF. Los resultados de la correlación
promedio de Pearson corresponden a una validación cruzada con 10
particiones con 80% para entrenamiento y 20% de prueba.
When the breeding values were predicted, it is observed that the models obtain similar predictions because only 4 of 12 combinations are different and three of them result in better predictions for the IBCF model, this correspond to PH trait in the Bed2IR and Bed5IR environments and GY trait in the Drip environment. In addition, the remaining combination corresponds to GY trait in Bed5IR environment that result in better prediction for the GBLUP model (Figure 8).
Meanwhile for the analysis performed using the phenotypic values, we can observe that in general the GBLUP without using the genomic information was the worst in terms of prediction performance than the other two methods (IBCF and GBLUB with genomic information) (Figure 8).
Two types of predictions using the two models GBLUP and IBCF are presented in Figure 9 with breeding values and phenotypic values, but with the cross validation, CV2. When predicting breeding values, remarkable differences are observed between both models, it is observed that under the GLBUP the best predictions were observed for traits DH and GY, while under the IBCF method the best predictions were observed under trait NDVI (Figure 9). While, for the results obtained when using the phenotypic values, we observe the same pattern, but the GBLUP model with or without genetic information produced similar predictive capacities (Figure 9).
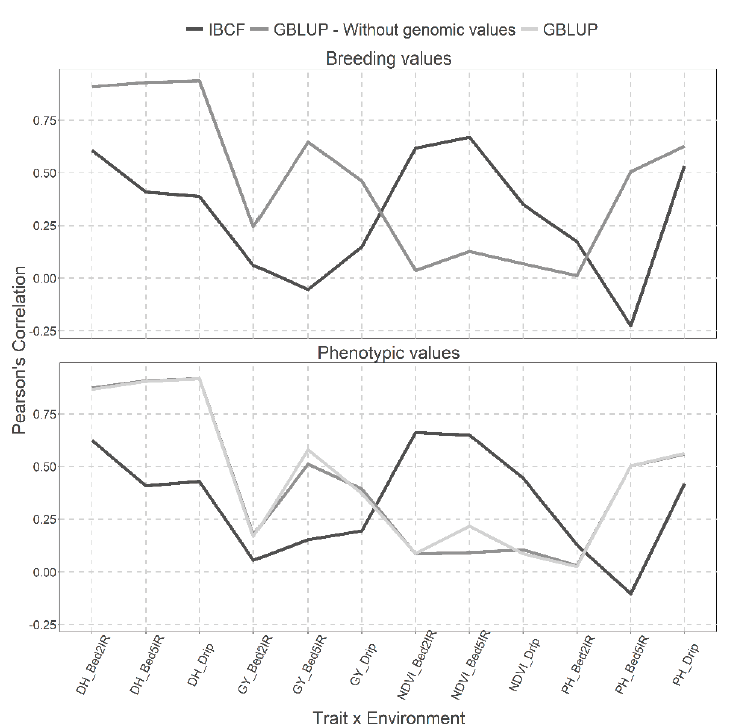
Figure 9 Prediction accuracy under CV2 with Pearson´s correlation for two models IBCF and
GBLUP, using phenotypic values and breeding values as the response
variable for the Wheat_IBCF data set. Pearson´s correlation results
correspond to each trait-environment combination.
Figura 9. Capacidad predictiva bajo CV2 con la
correlación de Pearson para dos modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos Wheat_ IBCF. Los resultados de correlación de
Pearson corresponden a cada combinación de rasgo-ambiente.
Finally, we compared the runtimes for the GBLUP vs. IBCF for Wheat_IBCF data using the breeding values and we found that the GBLUP takes 34.28 seconds to implement while the IBCF takes only 1.03 seconds, which means that the IBCF is 33.28 times faster than the GBLUP model (Table 2).
Wheat Iranian dataset
Figure 10 presents two types of predictions for both type of models, the first for predicting the breeding values and the second for predicting the phenotypic values. For these cases, CV1 cross validation has been used.
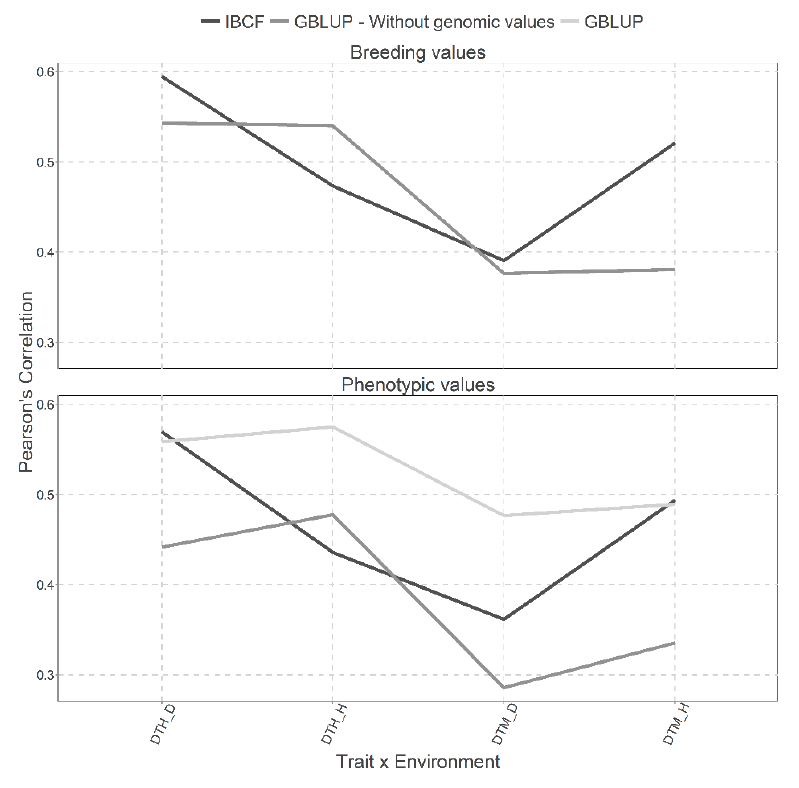
Figure 10 Prediction accuracy under CV1 with Pearson´s correlation for models IBCF and GBLUP,
using phenotypic values and breeding values as the response variable
for the Wheat_Iranian data set. The results of average Pearson
correlation correspond to a cross validation with 10 partitions with
80 % for training and 20% of testing.
Figura 10. Capacidad predictiva bajo CV1 con la
correlación de Pearson para los modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos Wheat_Iranian. Los resultados de la correlación
promedio de Pearson corresponden a una validación cruzada con 10
particiones con 80% para entrenamiento y 20% de prueba.
We can observe little gain between the scenarios when using breeding values against the scenarios using phenotypic values to predict for the Wheat Iranian data set. When the breeding values are predicted, it is observed that no great differences in the predictions between both models because 3 of 4 combinations are quite similar (Figure 10). When using the phenotypic values, it is evident that results obtained with the GBLUP model without the genomic values are better than those obtained with the IBCF model and the GBLUP model with genomic information. However, the IBCF was better than the GBLUP model with genomic information (Figure 10).
Two types of predictions were performed with the GBLUP and IBCF models in Figure 11 with breeding values and phenotypic values, but with the cross validation, CV2. We obtained better predictions under the breeding values scenario. Under predicted breeding values, the results obtained under the IBCF model are higher than those obtained by the GBLUP model in all the traits for all the environments (Figure 11). While, for the results obtained when using phenotypic values, the same pattern is observed, that is the IBCF was the best; however, the GBLUP model without the genetic information was better in prediction accuracy than the GBLUP with genomic information (Figure 11).
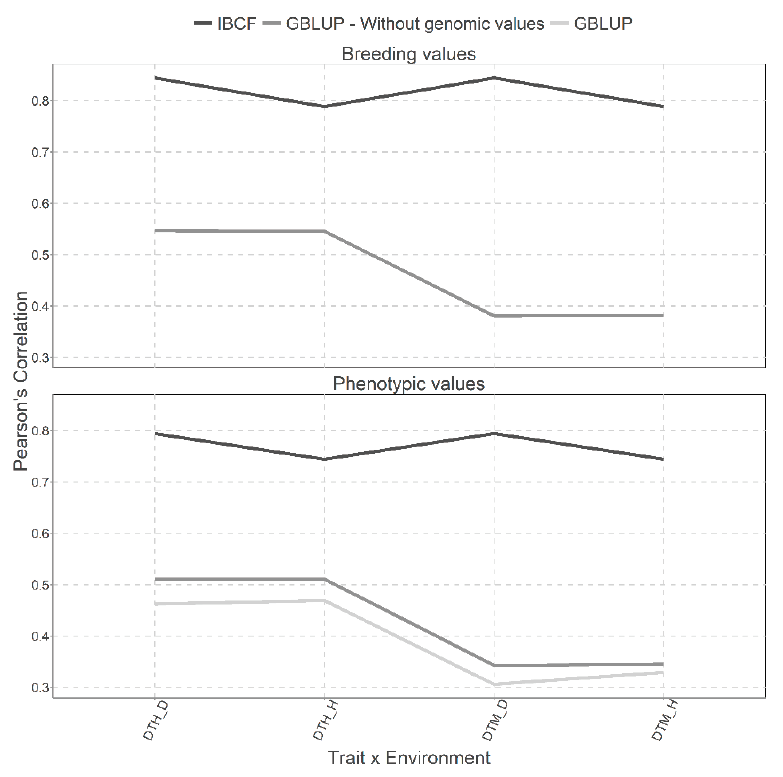
Figure 11 Prediction accuracy under CV2 with Pearson´s correlation for two models IBCF and
GBLUP, using phenotypic values and breeding values as the response
variable for the Wheat Iranian data set. Pearson´s correlation
results correspond to each trait-environment combination
Figura 11. Capacidad predictiva bajo CV2 con la
correlación de Pearson para dos modelos IBCF y GBLUP, utilizando
valores fenotípicos y valores genéticos como variable respuesta para
el conjunto de datos de trigo iraní. Los resultados de la
correlación de Pearson corresponden a cada combinación de
rasgo-ambiente.
Finally, we compared the runtimes for the GBLUP vs. IBCF for Wheat_Iranian data using the breeding values and we found that the GBLUP takes 1152.36 seconds to implement while the IBCF takes only 2.19 seconds, which means that the IBCF is 526.19 times faster than the GBLUP model (Table 2).
Time of execution between the models IBCF and GBLUP
Table 2 shows the execution times in seconds implemented by each model, showing that the IBCF model is able to process information more quickly, in the case of the smaller data sets used in this research, as: Maize, Maize_HEL and Wheat_IBCF show a difference ratio between the GBLUP and IBCF models between 15 and 33 times faster, while for the larger data sets used in this research, such as Maize_USP, Wheat_BGLR and Wheat_Iranian, a difference ratio between both models between 93 and 526 times faster is shown.
It is important to note that on average across data sets the GBLUP model requires 286.12 seconds to adjust the model, while IBCF requires only 1.68 seconds on average, that is, the IBCF method is 169.63 times faster than the GBLUP model.
Discussion
The results show that the IBCF methodology is competitive in terms of predictability compared to the GBLUP model. Montesinos-López et al. (2018) mention that the greater the correlation between the traits and between the environments, the better the performance of the model, and so their recommendation is emphasized for large data sets with many traits and moderately correlated environments. It should be noted that in the Maize and Wheat_BGLR data set, the IBCF methodology was better than the GBLUP model; on the other hand, in the Maize and Wheat_Iranian data set, the GBLUP model obtained better predictive capabilities when using the phenotypic values. Furthermore, the predictive capabilities have been similar between both methodologies when predicting the breeding values Maize_Hel, Maize_USP, Wheat_IBCF, Wheat_Iranian. Whereas, for phenotypic values in the Maize and Wheat_Iranian datasets the GBLUP model without the genomic values was the best, as well as in the Maize_USP, Wheat_BGLR datasets the GBLUP model with the genomic values was the best. In addition, the GBLUP methodology was less efficient in terms of prediction accuracy in the Wheat_USP and Wheat_BGLR datasets for phenotypic prediction, than the IBCF methodology, only when not taking into account the marker information in the GBLUP model. We also found that when predicting breeding values, the IBCF methodology performed better than when predicting the phenotypic values as shown in the results obtained by the Wheat_Iranian, Wheat_BGLR, Maize_USP, Maize_HEL & Maize data sets in the cross-validation analysis with random partitions.
There are reports that the IBCFF methodology works better in terms of predictive capacity when the number of traits and environments is considerably large and there is a moderate or high correlation between them. It is therefore suggested that this methodology be used in this context. However, here was tested in the extreme situation with few environments and traits and with low correlation between traits and environments and even in this context the predictions of the IBCF methodology were competitive to those of the GBLUP model. The lower prediction accuracy observed for the IBCF compared to the GBLUP model are compensated in terms of computational resources required since this methodology is extremely efficient in terms of execution time, since we found that it is at least 14 times faster than the GBLUP model. In addition, it is important to point out the IBCF methodology is not a model-based approach for this reason has the limitation that not allows estimating variance and covariance components of traits or environments.
Conclusions
This paper presents a comparison between the IBCF algorithm and the most popular genomic selection model called GBLUP using six real data sets. The results showed that the IBCF model had good predictive capabilities using only phenotypic values, although using breeding values, better predictions can be observed than the GBLUP model. However, in general the GBLUP model was better than the IBCF algorithm. However, we found that the predictions of the IBCF methodology are competitive with the advantage that is very efficient in terms of the computational resources required since we found that the IBCF methodology is at least 14-times faster than the GBLUB model. For these reasons, we believe that the IBCF is an interesting and practical tool for implementing genomic selection in breeding programs.











 nueva página del texto (beta)
nueva página del texto (beta)


