Introduction

The first studies to analyze the relationship between migration and poverty found that migration is an element often used to design poverty reduction strategies, given that migration is a kind of communicating vessel making it possible to balance the economic disparities observed between places of origin (poor) and destination (rich) (^{Ravenstein, 1889}). Municipalities with high percentages of population living in poverty would therefore be expected to be spaces that expel population (especially the poor population) to municipalities with high standards of living and therefore low poverty rates, meaning that the latter would become population attraction hubs. It should therefore be possible to identify the existence of at least two types of spatial groupings of municipalities or clusters: 1) expulsion regions, comprising municipalities with high poverty and emigration rates, and 2) attraction zones, containing municipalities with low poverty and high immigration rates.

According to one of the most common hypotheses, migration is used as a strategy to reduce or escape the poverty in which the migrant population lives in its place of origin. However, this hypothesis has been refuted by arguments showing that migration has a high economic, social, and human cost, which cannot be covered by populations living in conditions of poverty or simply that these populations do not migrate and when they do, they only move short distances (^{Fitchen, 1995}). These arguments suggest that populations living in poverty are unable to modify their living conditions through migration. Since migration is a fundamentally spatial phenomenon, the characteristics of the geographical environment are essential to explaining both the prevailing conditions of poverty in a given geographical space and the dynamics of migratory movements in terms of their direction, magnitude, distance, and temporality, as well as the economic, socio-demographic, and cultural determinants associated with the populations that decide whether or not to migrate (^{Delaunay, 2007}).

Several theories attempt to explain the relationship between migration and poverty, mainly from demographic and economic perspectives. In general terms, migration theories seek to explain the meaning, magnitude and temporality of migration flows through the analysis of individual decisions based on cost-benefit relationships, migration systems, network theories, and cumulative causation theories. However, these theories fail to consider migration as a spatial phenomenon and therefore omit the use and analysis of attributes associated with the geographical location of migrants in their places of origin, transit, and destination (^{Fawcett, 1989}). The combination of demographic and economic theories, and statistical techniques and geographic information systems (GIS) therefore provides a new paradigm for the study and analysis of migratory patterns able to incorporate the characteristics and attributes of migrants in terms of the variations caused by changes in their geographic location. In other words, the use of geographic information systems makes it possible to identify spatial clusters generated by the historical accumulation of migratory flows due to the existence of conditions that can be associated with a key set of socioeconomic determinants (^{Cushing, 1999}).

The migration-poverty relationship is mediated by employment, particularly the income level associated with employment, while the combination of the two (income and employment) is a function of the skills acquired during the training stage of individuals. These factors are used as predictors of the migration process. In this respect, the theory of human capital formation recognizes that labor opportunities and access to associated benefits, such as health services and quality housing, differ significantly between social groups and geographic spaces (^{Canales, 2017}). The individual decision to migrate is therefore based on both the skills acquired and the expected economic return. Individuals with higher qualifications and educational attainment will create a selective migratory flow, on the assumption that they will expect to obtain greater benefits in relation to the costs associated with migration (^{Stevens, 1999}).

The objective of this paper is to analyze the spatial distribution of municipal net migration balances in Mexico during the period 2015-2020, considering the effect of the percentage of population in municipal poverty observed in 2015, which suggests that migration depends on the poverty rates recorded in the recent past (^{Herrera Carassou, 2006}). The aim is to demonstrate that the creation of spatial clusters of municipalities constituting regions of population expulsion or attraction arises as a result of a migratory process responding to poverty rates reported five years earlier, in Mexican municipalities. This objective is achieved through the use of a series of spatial statistical methodologies, particularly the exploratory analysis of spatial data and Bayesian spatial models.

Migration and poverty theories

From a neoclassical perspective, economic rationality is an essential element in understanding the relationship between migration and poverty, in which the unit of analysis, “the subject,” seeks to maximize the utility derived from the decision whether or not to migrate (^{Fitchen, 1995}). The economic rationality of migration is therefore largely predicated on a cost-benefit analysis revolving around the differences in labor income observed between the places of origin and destination and the elements that could affect the associated costs and benefits.

Although income is not the only factor to consider in the complex network of elements involved in the decision to migrate, the theoretical foundations that could explain the intention to migrate suggest there is a rationality that leads people to maximize their benefits based on a decision-making model, in which they hope to achieve a maximum of benefits at the lowest possible cost (Homo Oeconomicus) (^{Molina Sánchez & Oyarsun de la Iglesia, 2008}; ^{Durand, 2004}). In particular, certain elements associated with migration decision-making are based on considering that the differences in expected labor income reflect the qualifications and educational attainment of the migrant, knowledge of the requirements for entering specific segments of the labor market in the potential places of destination, as well as information about the costs and risks associated with migration (^{Massey et al., 1994}).

The population living in poverty in Mexico is identified and measured by the Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL) (National Council for the Evaluation of Social Development Policy), which uses a methodology to gauge multidimensional poverty based on a combination of two approaches, 1) economic well-being, and 2) social rights, using the following definition:

A person is in a situation of multidimensional poverty when they are not guaranteed the exercise of at least one of their rights for social development, and if their income does not suffice to acquire the goods and services required to meet their needs (^{CONEVAL, 2019, p. 33}).

The multidimensional poor are those who live below the poverty line, and at the same time have one or more types of social deprivation. The poverty line defines the minimum income required to acquire the food and non-food basket of goods and services, while social deprivation includes educational lag, lack of access to health services, social security, adequate or quality housing and/or adequate spaces in the latter, basic services in the home and food access (^{Clark, 1986}). In Mexico, once the income level and degree of social deprivation have been determined, people can be classified as belonging to a 1) poor population, 2) population in a situation of multidimensional poverty, when their income is below the economic welfare line and they suffer from at least one type of social deprivation, 3) vulnerable population, when they experience one or more types of social deprivation, but their income is above the economic welfare line 4) vulnerable population due to income, when they do not experience social deprivation although their income is below the economic welfare line, and 5) non-poor and non-vulnerable population, when their income is above the economic welfare line and they do not experience social deprivation (^{CONEVAL, 2019}).

Although the decision to migrate is made individually, it tends to have repercussions at the familial, social, national, and international level, modifying population concentrations and economic conditions in the places of origin and destination of migration (^{Herrera Carassou, 2006}). In this respect, the neoclassical theory of supply and demand analyzes migration as a result of the differences between labor supply and demand. Poverty can therefore be explained as a temporary phenomenon resulting from the wage differentials between geographical areas. The difference is caused by the misplacement of labor (^{Cadwallader, 1992}; ^{Cushing, 1999}), which should eventually be corrected by the natural emergence of migratory flows. Neoclassical theory states that labor markets are homogeneous, meaning that the poor tend to move to destinations with higher wages, so that poverty will tend to decline in their places of origin, due to the labor shortage caused by emigration, which will eventually tend to increase wages (^{Stevens, 1999}).

At the individual level of decision making, microeconomic theory states that individuals make the decision to migrate, based on a cost-benefit analysis, rationally assessing destination options and selecting the one that maximizes their expected income, given their educational attainment, training and work experience and weighing up the costs and risks associated with relocation, labor insertion and adaptation (^{Basok et al., 2015}). Migration is therefore seen as an individual strategy designed to improve an individual’s standard of living. The new economics of migration regards the household as the basic decision-making unit. The underlying economic rationality therefore seeks to maximize benefits for the household unit, not just the individual. The new economics of migration considers the household the basic space of social and biological reproduction, operating at a second level of economic rationality (^{Canales, 2017}).

The strategy associated with resource allocation will therefore be based on a principle of risk minimization, rather than one of benefit maximization (^{Arango, 2003}). The new economic theory of migration therefore creates a strategy for the diversification of household income sources based on how many household members have the capacity to migrate, where the decision about which and how many household members should migrate is made by the family unit. The decision is designed to minimize the risk of the family unit lacking income, especially at critical moments in the family life cycle or during extreme economic crises, meaning that wage differentials between places of origin and destination are no longer a relevant factor in the decision to migrate (^{Foulkes & Newbold, 2008}). Households will therefore seek to send workers, not with the objective of maximizing their income, but with the aim of minimizing the household’s risk of falling into poverty or extreme poverty (^{Fitchen, 1995}).

The new economic theory of migration evaluates both the existing wage differences between the origin and the possible destinations of migration and the number and reliability of all sources of household income available in the place of origin and destination, to determine the number of household members who should migrate (^{Canales, 2017}). The decision to migrate and the number of household members who should migrate depends primarily on the relative economic position of the household in its community of origin, as well as its income distribution, meaning that the reliability of its source of income is more important than the amount (^{Basok et al., 2015}). This is because a reliable source of income will minimize the levels of relative deprivation, thereby reducing the risk of households falling into poverty (Canales, 2017).

At the meso decision-making level, once the migration process has been consolidated over time and space, the decision to migrate transcends both individuals and households, leading to the institutionalization of the migration process, in which a set of non-governmental organizations, legal offices, and migration agencies encourage and perpetuate migration processes, thereby detaching migration from its original determinants (^{Massey et al., 2008}). Institutionalization occurs once migration has been consolidated and presupposes the bureaucratization of the migration process, making the migration process slower and more costly. It implies open access by individuals (households) to the institutions responsible for undertaking migration procedures. However, access to institutions is subject to a series of costs and requirements that cannot always be covered by individuals (households) living in poverty (^{Bloomquist et al., 1993}), which can lead to the selection and stratification of migrants (Massey et al., 1994).

According to the theory of cumulative causation, migration can be seen as a causal-cumulative process that increases the income of migrants in the place of destination and the income of their families in the place of origin. This causes a demonstration effect, serving as an example of perpetuating migration as a process of causal accumulation and eventually creating and consolidating a migratory culture (^{Herrera Carassou, 2006}). In other words, migration not only affects migrants and their families, but also those who stay behind. On the one hand, migration reduces existing pressures in the labor markets of origin, and on the other, remittances improve the income and quality of life of the communities of origin (^{Clark, 1986}). Migration is therefore a poverty reduction strategy designed to enable and/or facilitate the movement of people, capital, and goods between places of origin and destination (^{Fawcett, 1989}).

The dual labor market theory assumes that migration is the result of the development of segmented labor markets that are especially attractive to immigrant workers from underdeveloped countries, mainly due to existing wage differentials (^{Bloomquist et al., 1993}). The duality of labor markets caused by the divergence between labor and capital needs has led to capital-intensive sectors utilizing the basic labor force, while labor-intensive sectors utilize the seasonal labor component, creating a dualism in the labor force. Jobs associated with the capital-intensive (primary) sector are generally filled by skilled workers, who constitute human capital and occupy stable jobs with benefits and high wage levels (^{Fergany, 1990}).

Conversely, workers in the labor-intensive (secondary) sector occupy unstable jobs, filled by unskilled personnel, lacking benefits and with low wages (^{Fitchen, 1995}). Secondary sector jobs are unattractive to local workers, given that salary confers status and prestige, meaning that migrant labor is often used to fill the demand deficit. Migration is caused by the attraction factors of the receiving countries, derived from the chronic demand for labor. It is in this sense that migration makes it possible to improve and/or overcome the poverty of immigrants’ families in their place of origin, while they generally continue to live in conditions of poverty in the place of destination (^{Beale, 2004}; ^{Lichter & Johnson, 2007}).

Macro-level analysis regards migration as an aggregate phenomenon. According to the push-pull theory, migration is a phenomenon created by the imbalance between labor supply and demand caused by differences in development levels between the places of origin and destination of migration (^{Arango, 2000}). This imbalance generates significant wage differences and therefore encourages the emergence of migratory flows, particularly those designed to attract highly qualified workers, who form part of the human capital of underdeveloped countries. In most cases, these countries do not have the capacity to retain these workers, mainly due to the existing wage gap (^{Bloomquist et al., 1993}).

It is important to note that the loss of human capital leads underdeveloped countries to further limit their development possibilities and thus perpetuate the migration-poverty cycle. The expulsion-attraction theory points out that the levels of underdevelopment and poverty present in the places of origin of migration represent the fundamental determinant for explaining the emergence and permanence of migratory flows whose destination is the labor markets of developed countries (^{Basok et al., 2015}).

The human capital theory, which emerged as an extension of neoclassical economic theory, states that the decision to migrate is made at the individual level based on the degree of qualification, education, and training, because their economic returns are expected to be decidedly higher than those of people without any degree of qualification, since migration tends to be selective (^{Molina Sánchez & Oyarsun de la Iglesia, 2008}). Thus, human capital theory partly explains the spatial concentrations of poverty observed in certain regions in terms of the observed patterns of migration (^{Delaunay, 2007}).

The magnitude of migratory flows can be explained by the emergence, development and expansion of migratory networks established between the places of origin and destination. The concept of migration network is based on developments derived from network theory that explain the existence of relationships between nodes, in this case migrants. In general, networks are constituted by relationships between relatives, friends, and neighbors (^{Foulkes & Newbold, 2008}). The network concept explains the ability of migrants to access different labor markets, especially in the places of destination. However, membership of a given network is often determined by the socioeconomic level of individuals, so that individuals living in poverty are generally less likely to belong to networks and therefore to have access to their benefits (^{Bloomquist et al., 1993}). The network concept makes it possible to integrate, analyze and explore relationships at different levels (micro, meso, and macro), while the analysis of belonging to one or more networks contributes to concepts such as social capital (^{Fawcett, 1989}).

In another paradigm, the world system theory assumes the existence of a global system of center-periphery relations, where the main determinant of migratory flows from the periphery to large industrialized centers is income disparity. The periphery is the source of raw materials and natural resources serving to cover the basic needs of the industrial centers that concentrate large amounts of capital and technology (^{Stevens, 1999}). Systems theory holds that it is the sustained presence of migratory flows that ends up forming a complex system of relations that encompasses, in addition to the flow of people, the traffic of capital, goods and services (^{Fergany, 1990}), under the premise that in the long term, all migratory flows tend to normalize (^{Arango, 2003}).

The existence of two flows is therefore recognized: a legal one comprising the free (or almost free) exchange of goods, services and capital, and a mostly illegal one related to the flow of people, subject to a large number of regulations and restrictions. Whereas in the center-periphery theory, goods and capital can flow in any direction, migratory flows run from the periphery to the center. In the systems theory, a migratory system comprises a region of reception formed by one or more countries, and a region of expulsion, both regions being linked by long-term migratory flows (^{Fawcett, 1989}). In both cases, migration flows run from the periphery (poor) to the center (rich), from rural to urban and from underdeveloped to developed regions (^{Durand, 2004}).

The discrimination, segmentation, specialization, and protectionism to which most labor markets are subject therefore reduce the possible destinations of migrants, especially those in conditions of poverty, forcing them to adopt differentiated migratory patterns (^{Beale, 2004}; ^{Lichter & Johnson, 2007}) that respond to determinants such as distance and the demand for unskilled jobs (Lichter & Johnson, 2007). The differential opportunity approach proposed by ^{Nord (1998}), arising from variations on neoclassical and human capital theories, suggests that the poor move mainly to poor regions, where the demand for unskilled, low-wage jobs predominates. In other words, the poor do not migrate to regions where there are better job opportunities, as predicted by neoclassical theory, but migrate to poor places where they find low-paying jobs, or on the contrary, they tend to remain immobile as claimed by human capital theory (Nord et al., 1995).

The differential opportunities approach states that labor opportunities for the poor differ geographically from those for the non-poor, so that poor households follow different rules for migration (^{Arango, 2003}). While the non-poor population migrates driven by attraction factors existing in the destination places, the movements made by poor people are, in many cases, determined by expulsion factors, so that the possible destinations are selected based on the possibilities of a rapid insertion into the labor market. The impetus for migration is not to improve income levels but to ensure minimum subsistence levels at the destination (^{Clark, 1986}).

In line with the arguments presented by migration theories, the disaggregated patterns of migration of the poor and non-poor modify the concentrations of poverty in specific regions, either in the sense that the poor migrate to developed regions (^{Sobrino, 2014}), in which case there would be a reduction in the number of people living in poverty in the regions of expulsion, or in the opposite direction. The evidence would therefore show an increase in the percentage of the population living in poverty in the places of origin of migration, in other words, in regions where high percentages of the population living in poverty are traditionally concentrated (^{Romo et al., 2021}). This would imply that the “differential opportunities” model of migration would refute the hypothesis that the population living in poverty migrates to places where they can find better living conditions (^{Berube & Kneebone, 2006}).

The study population and information sources

The study population comprises the total number of people residing in Mexico’s municipalities classified by their migration and poverty status. The data required to estimate the net migration balances as well as the municipal migration rates were obtained from the Intercensal Survey 2015, and the Census of Population and Housing 2020, both conducted by the Instituto Nacional de Estadística y Geografía (^{INEGI, 2015}, ²⁰²⁰) (National Institute of Statistics and Geography). It is important to note that the 2015-2020 municipal migration rates were estimated directly (with minimal corrections) from the quotient of the municipal net migration balance (difference between immigrants and emigrants) and the population at mid-period (June 31, 2017). Conversely, the data referring to the total population and the percentage of the population living in conditions of municipal poverty estimated as of 2015, were directly compiled from the estimates made by the National Council for the Evaluation of Social Development Policy (CONEVAL) of Mexico in keeping with the definition referred to in the previous section. In both cases, the information is assigned to the respective municipality based on its geographic key.

Municipal migration balances were measured through the question on the municipality of residence five years before the 2020 census date, included in Mexican censuses since 1970. This question made it possible to estimate the number of people who immigrated to a given municipality between March 15, 2015, and March 15, 2020 (census dates). Conversely, the number of people who emigrated from a given municipality was estimated as the difference between the initial population and the final population, plus births, minus deaths, plus immigrants, all registered between the two census dates. The calculation of migration balances between municipalities makes it possible to identify the places of origin and destination of migration. Once the municipal net migration balances had been estimated as the difference between immigrants and emigrants, the migration rate was estimated as the quotient of the municipal net migration balance and the total municipal population interpolated to September 13, 2017 (population at the midpoint of the intercensal period).

Exploratory analysis of spatial data

Exploratory spatial data analysis combines various statistical analysis techniques with geographic information system tools to identify the association between variables. In other words, it seeks to identify spatial distribution patterns of variables, outliers, and spatial clustering patterns. In general, exploratory analysis is useful for establishing hypotheses about the spatial behavior of observed data (^{Chasco, 2003}).

One of the most widely used statistics for the detection of spatial relationships is the global Moran index, which quantifies the levels of spatial autocorrelation between variables (^{Anselin, 1988}). Spatial dependence or autocorrelation is understood as the functional relationship existing between the observed levels of a variable at a given point in space and the observed levels of the same variable at neighboring points. The global Moran index therefore has the capacity to estimate the level of spatial autocorrelation existing between a variable and the global space, or between two variables and the global space (^{Getis & Ord, 1992}).

Another way of measuring spatial autocorrelation is through the local indicators of spatial association (LISA), which breaks down the global Moran index to identify local spatial association patterns, able to measure the effect of individual locations on the variable, which obviously increases the ability to identify spatial clusters (^{Anselin, 1995}). In particular, the LISA index makes it possible to identify the presence of hot clusters, also known as hot spots, as well as the existence of aberrant or atypical spatial observations. The LISA index takes values between -1 and +1. A high positive value of the index implies that the studied variable has high or low values similar to those of its neighbors, as a result of which it configures a spatial agglomeration. A high negative value of the local Moran index implies that the variable has an atypical spatial value in that location, meaning that its value is obviously different from that of its neighbors.

As a result, the local Moran map identifies five types of spatial clusters (^{Anselin, 1995}): 1) low-low: spatial units with below average values, surrounded by units with values below the average of the variable; 2) low-high: spatial units with below average values, surrounded by units with values above the average of the variable of interest; 3) high-low: spatial units with above average values, surrounded by units with values below the average of the variable; 4) high-high: spatial units with above average values, surrounded by units with values above the average of the variable of interest. These units form so-called hot clusters, and 5) non-significant, spatial units where the variable of interest does not achieve statistically significant levels of spatial autocorrelation (^{Getis & Ord, 1992}). Map 1 shows the distribution of each spatial unit and the way they are grouped or scattered according to the degree of similarity with their neighbors (^{Berube & Kneebone, 2006}).

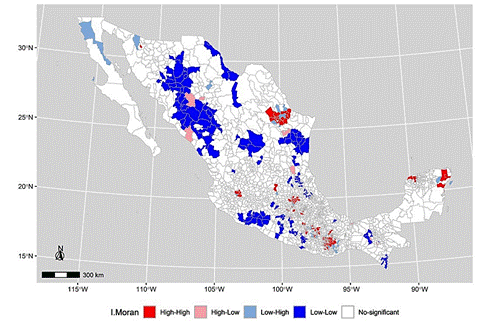
Source: Compiled by the author based on estimates made with R software (^{R Core Team, 2016}).

Map 1 LISA Index of Municipal Net Migration Balance, Mexico 2015-2020 

Maps 1 and 2 present the spatial distribution of the LISA index for the net migratory balance of Mexican municipalities during the period 2015-2020 and the proportion of the population living in municipal poverty conditions in 2015. Both maps show the presence of municipal clusters with high (and low) levels of migration as well as poverty.

Map 1 shows some hot clusters in red. These are clusters formed by municipalities with positive net migration balances, surrounded by municipalities whose migration balances are also positive and higher than the national average. The most important cluster, located between the states of Tamaulipas and Nuevo León, comprises the municipalities of Miguel Alemán, Mier, General Treviño, Doctor González, Agualeguas, Mina, and Garcia (Map 1). Similar clusters can also be observed in the states of Quintana Roo, Oaxaca, Puebla, and Sonora (Map 1). Map 1 also shows a series of low-high and low-low clusters indicating the presence of population expelling areas, presented in green and dark-green tones, located mainly in municipalities in the northern states of Mexico such as Sonora, Chihuahua, Coahuila, Tamaulipas and San Luis Potosí and a couple of clusters in the south of Mexico located on the coasts of the states of Guerrero and Chiapas, as can be seen in Map 1.

Map 2 shows the Moran index for the proportion of population living in municipal poverty in Mexico as of 2015. It indicates the presence of three large high-high clusters; a first high poverty concentration cluster located around the Lacandón rainforest in the State of Chiapas, the second located in the Yucatán peninsula, and the third in the states of Oaxaca, Guerrero, and Puebla, shown in red.

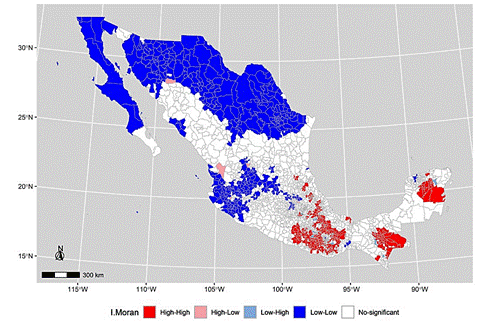
Source: Compiled by the author, based on estimates made with R software (^{R Core Team, 2016}).

Map 2 Moran Index for the Proportion of the Population Living in Municipal Poverty, Mexico 2015  

It is also possible to observe a series of clusters of low poverty concentration, surrounded by municipalities with high poverty levels (low-high), located mainly in the north of Mexico in the peninsula of Baja California and the states of Sonora, Chihuahua, Coahuila, Nuevo León, and Tamaulipas, as well as in the center of the country in the states of Jalisco and Nayarit, shown in light blue, in Map 2.

Map 3 presents the values of the Moran bivariate spatial autocorrelation index estimated for the net migration balance and the percentage of population in municipal poverty. The map shows a pattern dividing Mexico into two regions. In the northern region, a large, cold conglomerate is observed, drawn in blue and light blue, comprising the municipalities where low levels of emigration converge with low percentages of population living in poverty, with the exception of a series of municipalities located in the western Sierra Madre showing high levels of poverty and emigration, shaded in pink.

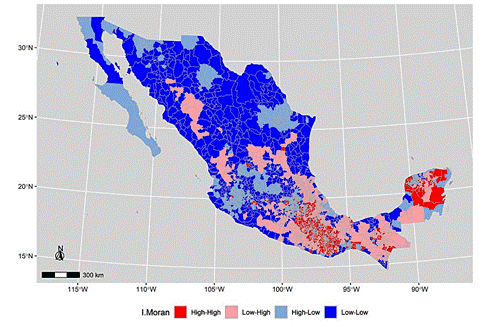
Source: Compiled by the author based on estimates made with R software (^{R Core Team, 2016}).

Map 3 Bivariate Moran Index of the Net Migration Balance during the Period 2015-2020 and Population in Municipal Poverty 2020, Mexico 

Methodology

The general formulation of a hierarchical Bayesian model assumes the existence of various components arranged in levels, where each level is represented as a stochastic process capable of transferring information between structures. In other words, hierarchical models seek to enhance the connections between observed data and the levels of the model to estimate a large number of unknown parameters, which is a useful strategy for the specification of complex models (^{Gómez-Rubio, 2020}). In this respect, latent Gaussian models constitute a particular case of hierarchical Bayesian models. Latent Gaussian models are defined through an additive regression structure in terms of a predictor ηi linked to the structure through a link function g(·), where

ηi=Egyi

In other words, the linear predictor models the expected value of a function of the response variable yi that follows a distribution given by an exponential family. The general structure of the predictor ηi is defined as follows (^{Schrödle & Held, 2011}):

ηi=β0+∑m=1Mβmxmi+ui+vi                       (1)

where each βi represents the linear effect associated with its corresponding covariate xi (^{Gómez-Rubio, 2020}). The ui term represents the spatially structured part of the model and the vi term captures the unstructured spatial effects (^{Moraga, 2019}).

The net migration rate for municipality i is modeled through a Gaussian distribution, which, for the case of municipalities in Mexico, is opted for using the standardized net migration rate, in other words, the migration rate with mean zero and variance one. The parameter μi represents the mean and s2 represents the variance (^{Blangiardo & Cameletti, 2015}). In this way, two latent Gaussian models were defined:

ηi=β0+ui+vi                                     (m0) ηi=β0+β1x1+ui+vi                              (m1)

the parameter β0 quantifies the average migration rate of all municipalities in Mexico. The term ui represents the spatial conditional autoregressive conditional structured (CAR) part of the model, whose distribution is given by the following:

ui|u-i~NΞi+∑j=1ndijuj-μj, si2                     (2)

Where Ξi represents the observed migration rate in municipality i and si2 the standard deviation (^{Rue & Held, 2005}), defined in terms of the number of neighbors si2=σu2 / #Νi. In this sense, dij weights spatial proximity, while σu controls for variation in spatially structured random effects (^{Moraga, 2019}). The term vi represents the unstructured spatial part of the model defined as vi~Normal0, σv2. Finally, for the case of model m1, the term represents the percentage of population in poverty conditions and β1 is the parameter associated with the variable x1.

The parameters estimated by models m0 and m1 are presented through the vectors θ1=β0,u,vand θ2=β0,βi,u,v while the parameters associated with the estimation of hyperparameters are represented by the vector ψ=τu,τv for both models, where the parameter τ=1σ2 estimates the inverse of the variance associated with each effect (^{Martino & Rue, 2010}).

The m0 and m1 models were implemented in R language (^{R Core Team, 2016}) from the integrated nested Laplace approximation (INLA) package (^{Rue et al., 2009}). The INLA package was chosen as an alternative to traditional Markov Chain Monte Carlo (MCMC) methods such as Gibbs and Metropolis-Hastings for estimating the posterior marginals of latent Gaussian models because INLA significantly reduces the estimation time of the models (Rue & Held, 2005) compared to MCMC. Whereas the base comparison model or null model m0 makes it possible to adjust the behavior of migration rates through a spatial field, in addition to the spatial field, model m1 incorporates the covariate proportion of population living in municipal poverty. The idea is to evaluate the contribution of the covariate in the spatial modeling of migration by using a statistical criterion for model selection enabling us to quantify both the quality of the data fit and the degree of complexity of the model (parsimony) (^{Akaike, 1998}).

Results

Table 1 presents the DIC criterion for model comparison and selection. The statistic indicates that the model with the lowest DIC should be selected. Thus, model m1 proved to be a better option for adjusting the spatial behavior of standardized municipal migration rates for Mexico for the period 2015-2020, relative to the null model m0, indicating that the proportion of people in poverty, represented through variable x1 (percentage of population in poverty), improves the adjustment capacity of model m1. In this type of context, a DIC difference of three to five points is considered significant, and therefore the observed distance of 113 DIC points statistically justifies the choice of model m1.

In general terms, the m0 model enables us to determine the distribution of the spatial random field defined from the behavior of standardized municipal migration rates. The modeling of the spatial random field depends directly on the covariance function and the spatial coordinates. In other words, the m0 model does not incorporate any covariate that modifies the relationship between the behavior of the variable and its spatial dispersion. The spatial modeling performed by the m0 model can be directly observed in Map 4B.

In contrast, the m1 model allows us to evaluate the effect of the proportion of the population living in municipal poverty on the spatial dispersion of standardized migration rates in Mexico’s municipalities. The addition of the spatial effect structured in each municipality therefore enabled the m1 model to reduce the DIC by 113 points, explaining the existence of a strong spatial autocorrelation and providing a lower value of DIC compared to the null model. The m1 model was therefore selected as the model with the best fit. At the same time, the estimates yielded by the m0 and m1 models made it possible to recognize the presence of spatial association patterns such as clusters with high or low migration rates associated with the presence, in the same regions, of high or low percentages of population living in poverty, as can be seen in Maps 4(b) and 4(c).

The fixed effect β0 of the m0 model, presented in Table 1, indicates that the average migration rate for the totality of Mexico’s municipalities between 2015-2020 was 0. In other words, it implies that the mean of the spatial field is zero, coinciding with the standardization of migration rates. In real terms, the estimated mean rate for Mexico’s municipalities was -4.56 migrants per thousand inhabitants, implying that the standardization shifted the mean -4.56 units. The estimated value of the parameter β0 for the case of model m1 (presented in Table 1 and 2) indicates, contrary to the previous model (m0), a clear overestimate of the standardized migration rate, given that it assigns a mean of 0.83, which contrasts with the standardized mean (^{Moraga, 2019}).

The estimates of the fixed effects of model m1 are presented in greater detail in Table 2, where the estimated parameter β1 indicates that a relative one percentage point increase in the population living in poverty conditions would imply a 1.3 percentage point increase in the emigration rate of the municipality, in other words, a 1.3 point reduction in the standardized municipal migration rate. This implies that the increase in poverty levels is directly associated with a significant increase in municipal emigration levels, as can be seen in Table 2. In addition, as noted above, the parameter β0 represents the average level of the net migration rate for all municipalities in Mexico once the effect of municipal poverty has been eliminated.

The results presented in Table 2 therefore clearly refute the hypothesis put forward in this research. According to the estimated result, municipalities with high levels of poverty tend to present negative net migration rates, a clear indicator that the population living in poverty in Mexico’s municipalities tend to emigrate from their place of origin, generally to places offering better living conditions.

Map 4 shows the spatial distribution of migration rates for Mexico’s municipalities in the period 2015-2020, from three perspectives: 4A, the observed municipal migration rate, 4B, the migration rate estimated by the spatial random field adjustment through the m0 model and 4C, the migration rate estimated by the Bayesian spatial model m1, including structured and unstructured spatial fixed and random effects. The differences observed between Maps 4A and 4C allow us to observe the adjustment capacity of model m1 and to determine its capacity to fulfill the purpose of smoothing the behavior of the rates, reducing and/or eliminating spatial random variations, while identifying real variations, which, for the case of standardized municipal migration rates, is reflected in an over-smoothing of the m1 model, derived from the adjustment of the conditional autoregressive part (CAR), which estimates the behavior of the spatial random effects of migration rates using preventive information from neighboring municipalities (^{Blangiardo & Cameletti, 2015}).

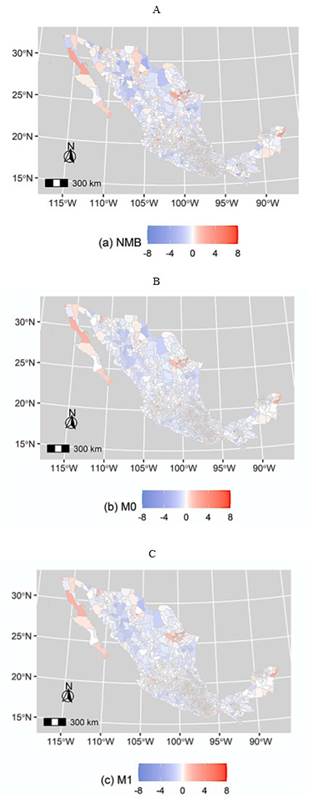
Source: Compiled by the author based on estimates made with R-INLA (Rue et al., 2009).

Map 4 Net Migratory Balance of Mexican Municipalities 2015-2020 

Map 5 presents the spatial distribution of the random effects generated by the ui term, which models the structured spatial part of the m1 model. The random effects were modeled through a conditional, autoregressive distribution defined from equation (2), so that the m0 model represents a convolution model making it possible to contrast the effect the covariates introduced into the m1 model, which may affect the spatial behavior of migration in the municipalities of Mexico. The estimates presented for the ui spatial effects are obtained on the assumption that when two areas share a common border, their random effects are correlated, which is why the model borrows information from neighboring areas to reduce the probability of producing aberrant estimates, or to obtain estimates for areas where no data are available.

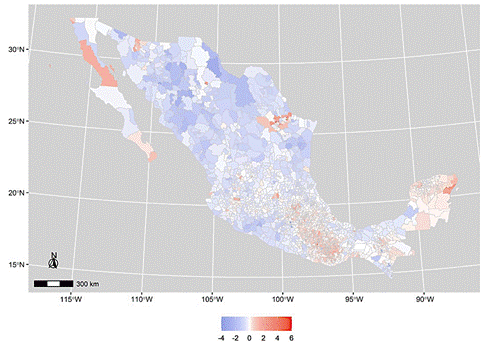
Source: Compiled by the author based on estimates made with R-INLA (^{Rue et al., 2009}).

Map 5 Model m1 Random Effects 

The spatially structured random effects represent the part of the model capturing the spatial heterogeneity related to migration rates across municipalities in Mexico. Map 5 presents the magnitude of change in the spatial variability of net migration rates. The spatial pattern of random effects can be seen in Map 5, which explains the large, correlated heterogeneity in municipalities where migration rates are high or low, supporting the choice of using a model that incorporates spatially structured random effects, enabling it to capture small-scale spatial differences and generate robust, reliable estimates.

In general, the spatial effects originated by the structured and unstructured variations of model m1 are jointly captured through the vector ςi=expξ=expui+vi where ξ records the spatial variations associated with the adjusted behavior of the standardized municipal migration rates once the effects of the covariate have been eliminated. In other words, the posterior mean probability can be estimated in terms of the risk associated with reaching a given level of migration ς (^{Schrödle & Held, 2011}) derived from the calculation of the conditional mean probability defined from the following:

P ςi>1  y ) ~ P ξi>0  y )

which evaluates the excess migration observed in municipality i (^{Moraga, 2019}), obtained from the estimates made by the m1 model. Map 6 therefore presents the posterior conditional probability associated with the spatial behavior exhibited by the net migration rates, whose spatial pattern makes it possible to identify regions with high levels of probability, associated with a high risk of migration and the presence of similarly high percentages of population living in poverty, such as those observed around the municipalities located in the region of the central valleys of Oaxaca and the mountains of Puebla (Map 6).

Source: Compiled by the author based on estimates made with R-INLA (^{Rue et al., 2009}).

Map 6 Probability that the 2015-2020 Municipal Migration Rate Exceeds the National Average Migration Rate in Mexico 

In addition to model selection criteria such as DIC or AIC, it is possible to evaluate the goodness of fit of different models by analyzing the proportion of variance explained by each model. The variance explained is obtained from the estimate of the marginal variance of the spatial component ξ which includes, as mentioned earlier, the structured spatial component ui and the unstructured spatial component vi. It is important to note that the variance of ui and vi are not directly comparable (^{Moraga, 2019}), so an empirical estimation of the posterior marginal variance of the structured spatial effects must be performed through the following:

su2=∑i=1nui-u-2n-1

where u- is the mean of the ui, so that the proportion of variance explained by the model is estimated as the quotient of the posterior marginal variance weighted by the sum of the variance of the unstructured effects and the variance of the structured effects, as follows:

Fracs=su2su2+σv2

the estimation of the fraction of explained variance is performed by the generation of 10 000 random samples taken from the marginal posterior distributions of τv and τu, for which the function inla.rmarginal implemented in the R-INLA package is used (^{Martino & Rue, 2010}).

Table 3 shows the proportion of variance explained by models m0 and m1. The results show that the m1 model captures 75% of the spatial variation of the net migration rates of Mexico’s municipalities, suggesting that three-quarters of the variability of municipal migration is explained by the spatial structure. Since the variance explained by model m1 is higher than that explained by model m0, one can assume that the covariate of proportion of population in poverty contributes one percent to the explanatory power of model m1.

Discussion

The m1 model shows that the population living in poverty in Mexican municipalities tends to emigrate, which is why the hypothesis that the poor population does not migrate cannot be sustained. However, this article does not clearly show the destination of migrants expelled from poor Mexican municipalities, but only allows to assume that they do so in the direction of the main economic development hubs in the country, such as Mexico City and Monterrey. In general terms, according to Map 4A, the migration rates indicate that 1 263 municipalities in Mexico are net expellers of the population (shown in blue) while only 241 are attractors (drawn in red), the remaining municipalities being considered to be in equilibrium. In other words, they do not attract or expel population, so that the same map only shows some conglomerates in red.

The implementation and estimation of two Bayesian spatial models for the distribution of standardized municipal migration rates made it possible to identify a series of clusters of population attraction associated with the poverty levels observed during the period 2015-2020. However, in 1 699 municipalities in Mexico, poverty affects fifty percent or more of their population whereas in only seven municipalities does the level of poverty affect less than ten percent of its population. The evidence presented, in regard to the dispersion of the migration and poverty rates of Mexican municipalities, refutes the results presented by ^{Nord et al., (1995}), indicating that the poor move mainly to poor regions, suggesting that the poor migrate to poor places where they find subsistence jobs.

However, the results shown in Map 4C point to the existence of migratory attraction hubs, where poverty levels are relatively lower than those observed in the regions of expulsion, refuting the hypothesis that immigrants move to poor places. However, since the article does not identify flows, the particular conditions of migrants in the places of origin and destination are unknown. However, it is logical to assume that, as ^{Nord (1998}) points out, migrants act on the impulse to ensure minimum levels of subsistence in the place of destination and seek rapid access to informal labor markets located mainly around the large metropolitan areas marked in red on Map 4C.

The article provides an initial approach to Bayesian spatial modeling at the municipal level of standardized migration rates in Mexico, in terms of the effects of poverty. The results make it possible to establish first-hand the spatial nature of municipal migration, as well as to identify a migratory pattern configured by large population expulsion regions and a small set of attraction zones that appear to concentrate significant percentages of the national population, particularly the metropolitan area of Mexico City, the municipalities surrounding the city of Monterrey, and Playa del Carmen. The immigration observed in the municipalities of Mexico can therefore be said to follow a pattern whereby the municipalities with the highest poverty rates are precisely those most likely to have negative migration rates, in other words, they are population expelling municipalities as observed in Map 6.

In the case of Mexican municipalities, migration is a multi-causal spatial phenomenon reflecting an array of both circumstantial and structural factors. Although the m1 model captured 75% of the variability of the phenomenon, it would therefore be useful to include associated explanatory variables, such as the average income of migrants in their places of origin and destination.

The use of spatial Bayesian models represents a significant improvement over exploratory analysis of spatial data, enabling to establish the existence of spatial correlation associations between variables. Limitations of the study include the lack of explanatory variables associated with the behavior of intra-municipal migration, particularly variables associated with the different levels of decision-making (micro, meso, and macro).

Conclusions

Migration between municipalities in Mexico from 2015 to 2020 occurred with greater intensity in municipalities with a higher proportion of the population living in poverty, and it is estimated that the population migrated to municipalities with lower levels of poverty. In other words, it was impossible to sustain the initial hypothesis that the population living in poverty does not migrate. On the contrary, municipalities with higher levels of poverty display higher migration rates. However, immigration patterns tend to concentrate in a few municipalities in Mexico, thereby raising relative poverty levels in the places of arrival (^{Nord et al., 1995}).

Although the causes of migration can be both circumstantial and structural, the levels of poverty observed in Mexico over the past 30 years appear to shape the structural conditions that encourage municipal migration. Poor municipalities may be expellers of the population, providing elements to invalidate the statement that migration intensifies concentrations of poverty in spaces with high percentages of poor population, given that the poor population remains immobile in these spaces (^{Foulkes & Newbold, 2008}).

The Bayesian spatial modeling approach used in the research made it possible to analyze the spatial distribution of municipal migration rates as well as to assess the impact of poverty on the spatial dispersion of rates, enabling the identification of clusters of municipalities that expel and attract population. In particular, it allowed the estimation of spatial random effects (both structured and unstructured) that model the spatial correlation inherent in the data (Map 5). Likewise, the combined use of geographic information systems and spatial statistical analyses derived from what is known as exploratory analysis of spatial data made it possible to obtain estimates that coincide with the results presented by Bayesian spatial models. This was particularly true for the analysis of the patterns of spatial autocorrelation derived from the estimation of indicators such as the Moran index for both migration rates and the percentage of the population living in conditions of municipal poverty.

Finally, it is important to highlight the growing influence of migratory flows on the size and structure of the population of Mexican municipalities, especially on municipalities with low population density, suggesting that migration is and will probably remain a fundamental factor for the demographic, economic and social configuration of the municipalities of Mexico. This type of research is therefore essential to understanding the migratory and population dynamics not only in terms of its spatial distribution but also of the effects caused by economic and social determinants. These effects arise from the places of origin and destination of migration in various contexts that determine the decision-making processes at multiple levels and must of course be captured, analyzed, and modeled, since they provide useful information for improving the living conditions of both migrants and those who decide to remain in their places of origin.