Introduction
Peters’s squirrel, Sciurus oculatus, is an endemic species from Central Mexico, with a small and fragmented population, located along the Trans-Mexican Neovolcanic belt and in areas of the Sierra Madre Oriental (Best, 1995; Hall, 1981; Monterrubio-Rico et al., 2013). Three recognized subspecies exist within its distribution range: a) S. o. oculatus is distributed in the eastern area, in the states of Queretaro, Hidalgo, and Veracruz (Ramos-Lara & López-González, 2017), b) S. o. tolucae is found in the southwestern area in the states of Guanajuato, Mexico, and Michoacán, and c) S. o. shawi in the northern area, in San Luis Potosí State (Best et al., 1995; Monterrubio-Rico et al., 2013).
Peters’s squirrel is an arboreal medium-large sized diurnal squirrel found in arboreal habitats consisting of coniferous-oak forest, between 1,500 and 3,600 m asl (Best, 1995; Valdez-Alarcón & Téllez-Girón, 2005). It is listed in the category Special Protection in Mexico by the NOM-059-SEMARNAT-2010 (Semarnat, 2010). The reason for its inclusion in this category is related with the high loss and fragmentation of its habitat for agriculture, and its use as a food resource, as occurs for other Mexican squirrel species in rural areas (Sánchez-Cordero et al., 2005; Thorington & Ferrell, 2006). Contrastingly, the IUCN listed Peters’s squirrel as Least Concern because of its widespread distribution and presumed large population. However, data about populations and their abundance are practically non-existent. Thus, further research and monitoring of different populations, as well as the design of an abundance index are necessary to know the real status of Peters’s squirrel populations.
On many occasions, the abundance estimation of species with small populations and fragmented distribution requires exhaustive and expensive fieldwork, so this represents a major limitation to assessing threats to a population and its subsequent conservation status (Balmford et al., 2003; Dixon et al., 1998). Thus, the use of camera traps to monitor these species has provided a useful tool for improving and facilitating the survey of elusive species, consisting of small and remote populations (Delibes-Mateos et al., 2014; Munari et al., 2011). Camera trap studies of mammals have mainly focused on medium and large mammals (O’Connell et al., 2006; Ridout & Linkie, 2009), and rarely on small mammals (McDonald et al., 2015; Paull et al., 2011; Welbourne et al., 2015) or other species (Ariefiandy et al., 2014; Suwanrat et al., 2015). Its use for the study of small mammals such as squirrels is limited because of their low detectability due to small body size and reduced home range. However, camera traps can provide an efficient tool for assessing rodent species and should be explored (De Bondi et al., 2010; Di Cerbo & Biancardi, 2013; Welbourne et al., 2015).
Camera trapping data combined with new methodologies for statistical analysis enable characterizing the status and changes among populations of a species (Ahumada et al., 2013; Fancourt et al., 2015). Models based on presence/absence (or detection/non-detection) data have been developed to estimate abundance and densities considering imperfect detections (Royle, 2004; Royle & Nichols, 2003). In many occasions these methods seem to be more accurate and require less effort than other abundance estimation methods and have been adopted in many surveys and monitoring research projects, providing an effective method for studying the change in species’ abundance and distribution across time and space (Ariefiandy et al., 2014; Linden et al., 2017; Royle et al., 2005; Suwanrat et al., 2015). The Royle-Nichols heterogeneity models to estimate abundance, at the same time allow evaluating the relationship between abundance and probability of detection with the human-environmental covariates (Royle & Nichols, 2003; Royle et al., 2005; Stanley & Royle, 2005). We used Royle-Nichols model with detection-non-detection data collected from camera trap surveys as a tool to study an isolated population of the threatened Peters’s squirrel in Central Mexico. Our study aimed to estimate the abundance of Peters’s squirrel and identify the ecological and human factors that could be modifying or limiting its abundance and distribution. These results can be used as a tool for the conservation of Peters’s squirrel in the pine-oak forests of Central Mexico.
Material and methods
The camera trap survey was carried out in a management unit for wildlife conservation, located in Rancho Santa Elena (Huasca de Ocampo) and San Juan (Epazoyucan) in the southern part of Hidalgo State (20º08’ N, 98º31’ W), near to the National Park el Chico where Peters’s squirrel had recently been observed (Hernández-Flores & Rojas-Martínez, 2010). Both areas include approximately 1,500 ha of land surrounded by small human settlements. Study areas are populated by a homogeneous pine forest with dispersed oaks and open areas with dry scrublands between 2,300 and 2,900 m asl, with highly varied topography.
From October to December 2014, the camera trap sampling was carried out to detect the animal species present in the study area. Briefly, 20 triggered digital cameras (in each area; 6 Cuddeback® Attack series, Non-Typical, Inc., Green Bay, Wisconsin, USA, and 4 Wildview® Xtreme series, Grand Prairie, Texas, USA) were uniformly spaced throughout the study area, following a grid-sampling scheme that averaged 1.1 km (780 -1,597 km interval) between cameras. The cameras were installed on trees at approximately 30-50 cm height, without any rodent specific bait. We programmed the cameras to a minimum time delay (0 seconds) between consecutive photos to maximize the number of photos taken per captured individual. Cameras were maintained at the site for 50 days and revisited every 9-10 days. Consecutive images of the target species within 24 h intervals were considered as the same event, whereas those separated by longer intervals as independent events.
We used the species detection-non-detection data to estimate abundance with the Royle-Nichols (hereafter RN) model (Royle & Nichols, 2003) in a Bayesian approach (Royle & Dorazio, 2008). RN model is based on the idea that if detection probability should depend on abundance, then repeated counts could inform about detection and abundance. Therefore, the information about abundance comes from the observed level of heterogeneity among sites in the probability of detecting the species, or in other words, it is an abundance-induced heterogeneity model. If an individual i in a site j is detected with probability r j , then the link between species detection p ij and abundance Ni is:
The assumptions for RN model are: i) the probability of detecting an animal at a camera trap is a function of the number of animals at that site; ii) the detection of one animal at a site is independent of the detection of any other animals, and iii) all individuals are equally detectable. Considering the distance between cameras and that Peters’s squirrel is not a gregarious species it is reasonable assuming the capture events were independents.
We incorporated potential of n covariate effects (COVnij) in probability detection p ij on each site i and occasion j using a logit link, specified as:
We utilized a similar covariate structure for the abundance (COVn_ABij) specified as:
We used Kuo and Mallick (1998) indicator variables selection approach to select the best candidate model concerning the use of both parameters -detection w and abundance wa- in the models (Royle et al., 2014). We evaluated the performance of all candidate models using 9 different attributes of habitat as covariates (Table 1).
Table 1 Covariates used to predict the abundance and detectability patterns of the Peter´s squirrel within the sub-population in the Sierra de las Navajas, Hidalgo State, México. We use the abbreviations described in this table in the text.
| Covariate | Abbr. | Description | Range |
| Habitat | HAB | Binary assignment of forest or open area habitat type. | 0-1 |
| Canopy cover | CPY | Coverage percentage of the trees in a 100m radius from the camera trap site. | 0-90 % |
| Scrub coverage | SCV | Coverage percentage of the scrub in a 100m radius from the camera trap site. | 10-90 % |
| Logging activity | LOG | Binary assignment of the presence of logging activity in the camera trap site in the last year. Pruning, crown and low thinning. | 0-1 |
| Elevation | HI | Elevation of the camera trap site | 2,332-2,872 m asl |
| Distance to water | DW | Distance between the camera trap site and the nearest permanent water mass. | 25-1,131 m |
| Distance to settlements | DH | Distance between camera trap site and the nearest permanent human settlement. | 232-3,218 m |
| Presence of carnivores | PRED | Binary assignment of presence or absence of grey fox and ringtail in the camera trap site. | 0-1 |
| Trail | WAY | Binary assignment of trails with a bare substrate | 0-1 |
Posterior probability distributions of model parameters were estimated using a Monte Carlo-Markov chain (MCMC) algorithm implemented in program JAGS (Plummer, 2003). We called JAGS from within program R (R Core Team, 2017) with the library jagsUI (Kellner, 2015). All prior distributions were uninformative distributions specified to have little influence on the posterior probability distributions, due to the data dispersion. To improve the convergence in detection we censored the priors for the covariate parameters using the interval (-3, 3). Estimates were based on 3 chains of 50,000 iterations with 10,000 burn-in iterations and a thin rate = 1. Convergence was diagnosed for the selected model by visual inspection of the MCMC chains for adequate mixing and stationarity and by using the Gelman-Rubin statistic (with values < 1.1 indicating convergence [Gelman et al., 2003]).
At each camera trap location, we recorded the factors (covariates) associated with habitat, landscape, human presence and predator presence (Table 1). Covariates were as follows: habitat type (HAB) as forest or open areas; proportion (%) of tree canopy cover (CPY) and scrub cover (SCV); logging activity (LOG) comprising the presence or absence of logging activity (forest thinning) during the last year at camera trap location; elevation (HI) of the camera location; distance of camera location to permanent water (DW); distance of camera location to nearest human settlement (DH); trail (WAY) indicating the camera placement on a trail with a bare substrate; and detection or non-detection in the camera trap location of the more abundant predators (gray fox, Urocyon cinereoargenteus, and ringtail, Bassariscus astutus; PRED), as these represented the main predators at the study area. Habitat factors were obtained during camera installation day and sampled at a radius of 100 m from the camera, for each survey site (Table 1).
The detection of carnivores was obtained from the camera trap data. We calculated landscape factors using the Geographic Information System (QGIS version 2.8.1, QGIS Development Team, 2015; Table 1). We eliminated any covariate that correlated highly (> 0.6) with other covariates to avoid multi-collinearity. In this way, the outcome of correlations enabled us to eliminate HI, HAB, DW, SCV as these correlated highly with other covariates that represented a more biologically meaningful explanation. All the continuous covariates were standardized to z scores before the analysis (MacKenzie et al., 2006). PRED, LOG and WAY were included as a binomial factor (1, 0) for all camera trap locations.
Results
The total sampling effort was 980 trap-nights. Peters’s squirrels were detected in 9 out of 20 sites (naïve occupancy of 0.45) with a capture success of 2.4 captures/100 trap nights. The average time before the first capture was 23.56 (SE = 13.89) days. Besides Peters’s squirrel, other 12 mammal species were detected during the sampling period: domestic cat (Felis silvestris catus), domestic dog (Canis lupus familiaris), bobcat (Lynx rufus), ringtail (Bassariscus astutus), gray fox (Urocyon cinereoargenteus), coyote (Canis latrans), Virginia opossum (Didelphis virginiana), hooded skunk (Mephitis macroura), hog-nosed skunk (Conepatus leuconotus), western spotted skunk (Spilogale gracilis), nine-banded armadillo (Dasypus novemcinctus) and eastern cottontail (Sylvilagus floridanus); all these species were previously recorded in the area (Sanchez-Rojas et al., 2016).
The results showed a Peters’s squirrel mean site abundance of λ = 0.89, SE = 0.27 individuals and daily detection probability was ρ = 0.034, SE = 0.005. The most supported model included PRED+DH as a predictor (Table 2). PRED was the covariate most important for the squirrel detection probability with negative relation (β = -1.46, 95% BCI = -2.59 -1.45). Model selection indicated DH as the best predictor for the squirrel abundance (β = 1.13, 95% BCI = 1.12 - 1.82) in the most supported model and showed a positive relation. Another model with high support was WAY+PRED+DH (Table 2). The second model supported included also WAY (β = -1.13, 95% BCI = -2.69 - -0.29) as a negative association with squirrel detection but with a lower weight. Other factors had limited model support (Table 2).
Table 2 Kuo and Mallick model weight comparison and selection of the best candidate model including abundance and detection parameters. The results in the first approach are post-process model weights in a comparison of all possible models. Covariate abbreviations are described in the text and Table 1. Only models with > 0.01 weight are represented. The selected model corresponds to the top row.
| Model | Weight |
| λ (DH), ρ (PRED) | 0.208 |
| λ (DH), ρ (PRED+WAY) | 0.202 |
| λ (CPY), ρ (PRED+WAY) | 0.102 |
| λ (CPY), ρ (PRED) | 0.070 |
| λ (CPY+DH), ρ (PRED) | 0.060 |
| λ (CPY+DH), ρ (PRED+WAY) | 0.056 |
| λ (LOG+DH), ρ (PRED+WAY) | 0.043 |
| λ (LOG+DH), ρ (PRED) | 0.042 |
| λ (DH), ρ (WAY) | 0.037 |
| λ (CPY+LOG), ρ (PRED+WAY) | 0.032 |
| λ (CPY), ρ (WAY) | 0.024 |
| λ (CPY+LOG), ρ (PRED) | 0.019 |
| λ (DH), ρ (.) | 0.016 |
| λ (CPY+DH), ρ (WAY) | 0.014 |
| λ (CPY+DH+LOG), ρ (PRED) | 0.013 |
| λ (CPY+LOG+DH), ρ (PRED+WAY) | 0.013 |
| λ (DH), ρ (PRED) | 0.010 |
Discussion
The paper provides a case study, where an approach is used that is much more accurate to assess the detection of Peters’s squirrel in a very anthropic environment. Likewise, this methodology facilitates comparison, improvement, and extrapolation to other populations or similar species. The expansion of these surveys throughout the entire squirrel distribution area, during different seasons over time, will help reveal population dynamics and factors that influence abundance (Ahumada et al., 2013). The abundanceoccupancy heterogeneity models then appear effective as estimators of abundance (Ariefiandy et al., 2014; Linden et al., 2017; Royle & Nichols, 2003). They are thus useful for detecting population trends, species interactions, how management affects these, or for predicting the effects of future land-use changes upon abundance and distribution (Ahumada et al., 2013; Clare et al., 2016; Suwanrat et al., 2015; Towerton et al., 2011).
The use of camera traps with detection/non-detection models are shown as an efficient and standardized tool for monitoring rare and little-known species, as well as being an important instrument for evaluations relating to the Red List conservation status, and for the management policy of these species (de Oliveira et al., 2012; Di Cerbo & Biancardi, 2013; Linkie et al., 2007; McCarthy et al., 2012; McDonald et al. 2015). This type of approach to abundance could be of great use to standardize the evaluations of the species, mainly on a regional scale (Gärdenfors et al., 2001). Similarly, information that is derived from multi-species studies or relating to other target species can provide very important data to expand knowledge and monitor these species populations (Clare et al., 2016; McCarthy et al., 2012). Therefore, new types of knowledge resulting from monitoring and sharing data about these species may promote research collaboration for the conservation of species that are not usually the objective of scientific studies.
The detection probability of Peters’s squirrel in our study was low, but the number of temporal replicates (50) is enough if we use as reference the number of optimums of replicated surveys for occupancy models (Guillera-Arroita et al., 2010). Biases in the study method must be taken into consideration; for example, the fact that it was only possible to detect a squirrel if it was on the forest ground. Yet, it is very important to include detectability in abundance models (Royle et al., 2005).
Models indicate that detection probability was affected by the presence of the main carnivore’s species in the area, the ringtail and the gray fox (Table 2). It is important to consider the high vulnerability of Peters’s squirrel when they are on the forest ground. Among species of the same genus in other temperate forests, up to 85% of mortality is caused by direct predation, and the greatest risk occurs when squirrels are on the forest ground (Lima et al., 1985; Vander Haegen et al., 2013). The low detectability of the squirrel in the sites with the detection of carnivores could be due to behavior modification to minimize the predation risk in this site avoiding going down to the ground. Also, the negative relationship between detection probability and the factor WAY could be to reduce the encounter probability with humans and carnivore species that mainly use trails to move. Additionally, it seems logical that part of the species detectability at one site could be related to the number of individuals visiting the camera location and the number of visits by a specific individual, which is determined by the specific behavior of that individual. In the case of the squirrel, the individual anti-predatory behavior of each squirrel can affect the estimates of abundance and detectability.
The RN models allow us to decompose the numerical and behavioral processes (Clare et al., 2016). In our case, detection probability appeared to be related to behavioral adaptations to carnivore and human presence; for example, descending to the forest less frequently to be less exposed. Concerning the abundance of Peters’s squirrel in this part of the Sierra de las Navajas, models indicated that the distance to settlements influenced the abundance and distribution of the squirrel (Fig. 1). Our results showed a strong decrease in the squirrel abundance in areas close to the human settlements (Gill & Sutherland, 2000). The reduction of the squirrel abundance may be due to behavioral factors concerning its descent to the forest floor or may be related to subsistence hunting, which is known to occur in our study areas (Hernández-Flores & Rojas-Martínez, 2010).
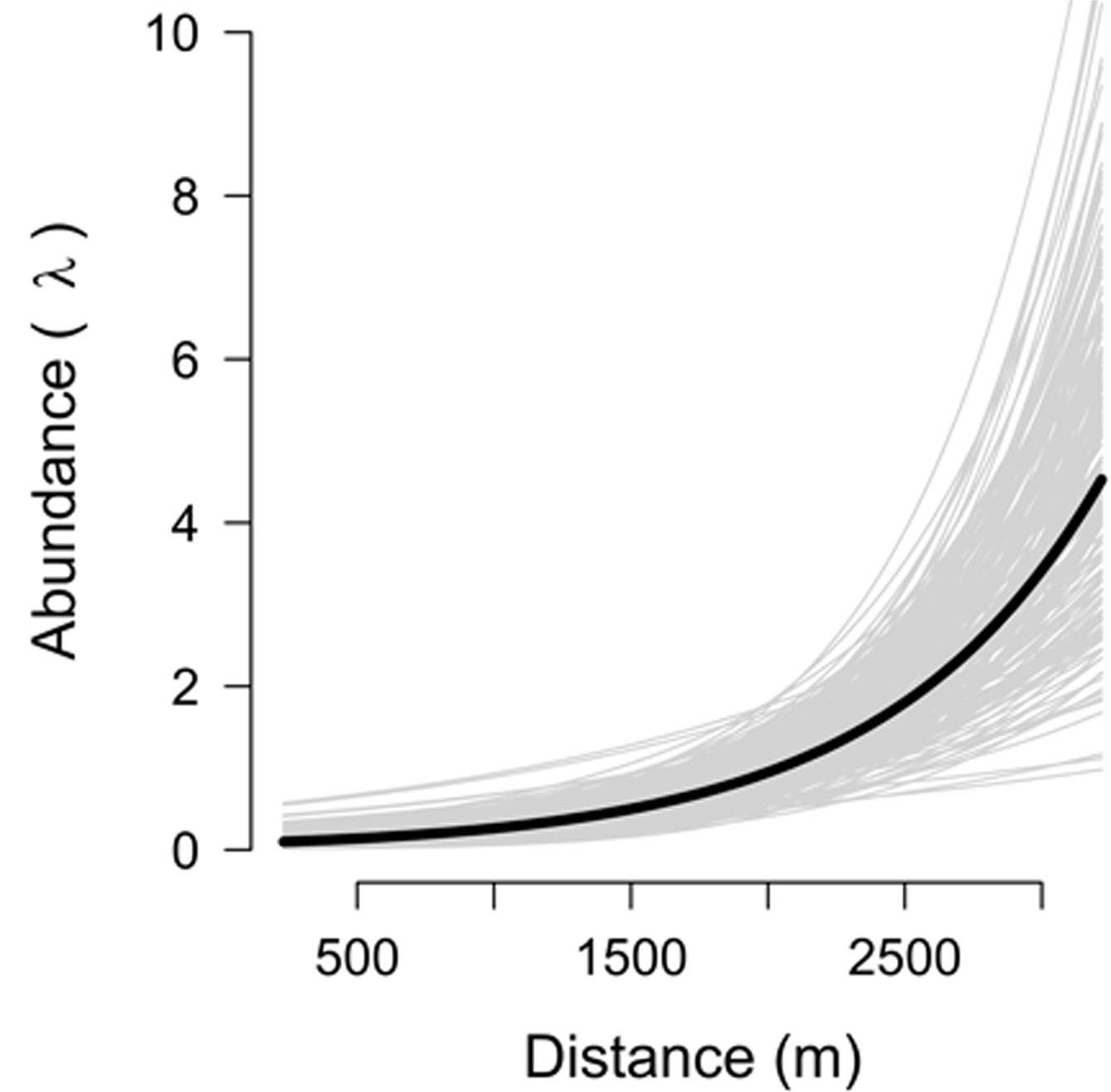
Figure 1 Relationship between abundance of Peters’s squirrel and distance to nearest human settlements (DH). Thick black line = mean; thin grey lines = relationships based on a random posterior sample of 200 to visualize estimation uncertainty.
Another possibility is the presence of domestic dogs and domestics cats in the areas nearest to the human settlements that could influence negatively squirrel abundance (Van Der Merwe et al., 2005). Our camera trap data showed an increase of domestic cats and dogs’ abundance in the nearest 1.5 km radius of distance to the human settlements. The data also show an important activity overlap between the Peters’s squirrel and the domestic carnivores (unpublished data), both mainly diurnal (Ramos-Lara & López-González, 2017). It is important to highlight that other variables not included in the models could affect the squirrel population.
Our results also showed that Peters’s squirrel is common in these temperate forests, so it is confirmed that although it is an endemic species, in this part of its distribution it has no serious conservation problems. Several anthropic factors are influencing the squirrel abundance and distribution and could represent potential threats in this part of Mexico if deforestation and habitat fragmentation continue. Adequate forest habitat management and maintenance of areas with difficult human access may aid conservation of the Peters’s squirrel population. Research on habitat affinities and resource selection would enhance effective covariate selection for abundance models and allow more effective forest management for the species. Thus, it is very important to increase knowledge about the ecology of Peters’s squirrel and the threats to its conservation.











 nueva página del texto (beta)
nueva página del texto (beta)


