1. Introduction

Throughout the history of Classical Mechanics, the simple pendulum represents one of the most important issues. However, the problem is usually solved by doing the typical approximation of small angles (sinθ ≃ θ). The large angle case is normally avoided but it is a well-known fact that the solution can be reduced to an integral which involves the complete elliptic integrals of the first kind ^1,2. Few years ago, some authors proposed some empirical methods, arithmeticgeometric mean techniques and approximate approaches for finding the period for high angles ^3-7, but for angles bigger than 100° the methods fail. Recently, other authors developed different techniques based on approximate methods which give much better results ^8-11. In particular, it must be highlighted the work done by Beléndez et al⁸ since they found practically perfect periods up to 163° with an error of 1% using MacLaurin series expansion. However, for larger angles the method begins to separate from the exact period and the calculation includes too much terms. The purpose of this article consists in developing a technique which deduces the periods for angles bigger than 170° with a high degree of accuracy and it shows the importance of using the conservation of the energy as a constraint in an approximation method when a nonlinear problem is analyzed.

Recently, Salinas et al¹² by means of substituting the cosine function by a polynomial in the energy equation, deduced the trajectory of the pendulum by a simple integration. An intermediate step is necessary for obtaining the trajectory for angles up to 85°. Due to the symmetry of the trajectory, the technique can be extended to angles close to 95° and by using a third step, with different parameters, the method can be generalized to bigger angles. Unfortunately, for practical purposes, the proposal becomes impractical. However, for angles bigger than 170°, a simple polynomial can be used to obtain a great similitude with the cosine function. Nevertheless, obtaining the trajectories and the periods is not satisfactory. The small difference between the proposed polynomial potential and the real potential in the neighborhood of the maximum angle, is the cause of the failure of the method. The essence of the method will consist of giving an approximate function of the potential energy as much as it is possible but with the constraint of minimizing the error in the critical point. Other kind of polynomial has to be proposed. Indeed, by using a different but similar polynomial which leads to simple integrations too, a much more accurate result is obtained between 170° and 180° which is almost equal to the exact solution.

This work is organized as follows: in Sec. 2, a simple polynomial method is performed in order to obtain the trajectories for angles close to 170°. Since the method fails, it is explained why another kind of polynomial has to be used. In Sec. 3, a different polynomial, but similar to the used in Sec. 2, is proposed. By using the minimization of the standard deviation, the result matches quasi perfectly with the exact solutions and it improves all the previous methods. In Sec. 4, some concluding remarks are done.

2. The Polynomial Method

The simple pendulum consists of a massless rod fastened at one end which freely rotates in a plane and a pointed mass at the other end. The conservation of the energy can be written as

where E, m, g, θ and l represent the energy, the mass, the gravity, the angle with the vertical and the length of the pendulum. Then,

By supposing that the maximum angle occurs at θ_o and θ_o = 0, obtains

Expressing the time as a function of the angle,

This represents an elliptic function. Many authors proposed different methods, usually approximations, in order to approach simple solutions without using any difficult function and giving a simple analytical approach to the trajectory ^3-12. In particular, Salinas et al¹² developed an analytical method based on substituting the cosine by a polynomial which leads to a simple integral. However, the approach is not enough good from a certain angle and a second step is required obtaining the trajectory for angles less than 95°. For larger angles, a third step must be done so that the method becomes impractical. Nonetheless, for angles between 170° and 180°, a polynomial which matches the cosine function with a high degree of accuracy, can be found. Let us summarize the principal idea of the method ¹²: first, the function cosθ − cosθ₀ is approximated by a polynomial,

where a and b are setting parameters. Since cos0 = 1, it is necessary that a = 1 − cosθ₀. If we put b=1/θ02, the polynomial coincides with cosθ at θ = θ₀, but for other angles, the polynomial differs greatly from the cosine function. Therefore, b should be adjusted to give a good approximation. As a consequence of it, the polynomial approximation is not good enough for angles lower than the maximum angle θ₀ (lower than 85°) and a cut-off angle, θ₁, is required and a second step must be improved ¹². Nevertheless, for higher angles close to 170° the polynomial can be fixed very close to the cosine function and a second step is apparently not necessary. Therefore, put

Then, Eq. (4) can be expressed as (changing the initial time t_o =0)

This integral is easily solved,

Finally, we arrive at

It has to be noted that b is restricted to b < (1/θ²).Unlike maximum angles about 85°, for maximum angles bigger than 170° the polynomial can be fixed fitting the parameter b by minimizing the standard deviation between the polynomial and cosine function. The found polynomial practically coincides with the cosine function (see Fig. 1).

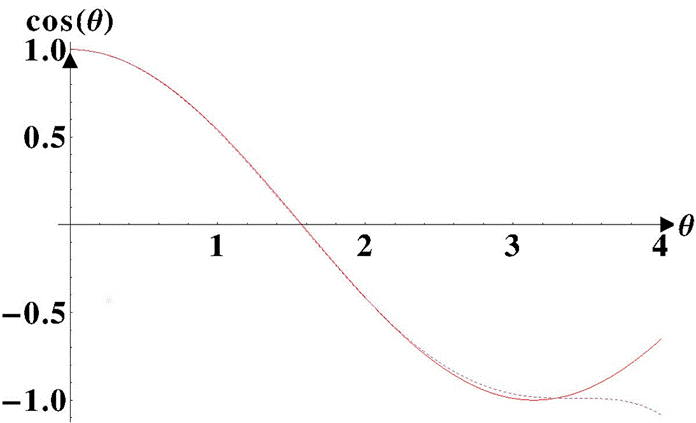
Figure 1 The dashed curve corresponds to the polynomial with b = 0.085 and θ₀ = 171.9°. The other curve is the cosine function. 

In Fig. 1, it is easy to notice that the difference between the polynomial and the cosine function is negligible and we expect to obtain a good trajectory. However, by analyzing Eq. (9), some aspects must be mentioned. The first one is that at the maximum angle, the angular velocity does not vanish. Indeed, by using Eq. (7), the angular velocity can be expressed as

For θ₀ = 171.9° = 3.000 rad, 1/θ02=1/9≃0.111 differs from the value of b = 0.085 used in the polynomial for this angle. Therefore, the obtained trajectory cannot represent the real since the angular velocity does not vanish at the maximum angle. Moreover, if we calculate the angular velocity in this case, θ₀ = 171.9°, g = 9.8 m/sec² and l = 1 m, we obtain

By comparing it with the typical angular velocity of the motion of 3 rad/sec, it represents the 23.7% of the basic motion which is unacceptable. As a consequence of this, the obtained period will be far from reality. Indeed, the period of the motion is equal to

being t₀ the time to reach the maximum angle θ₀ from the initial θ = 0 (see Fig. 2).

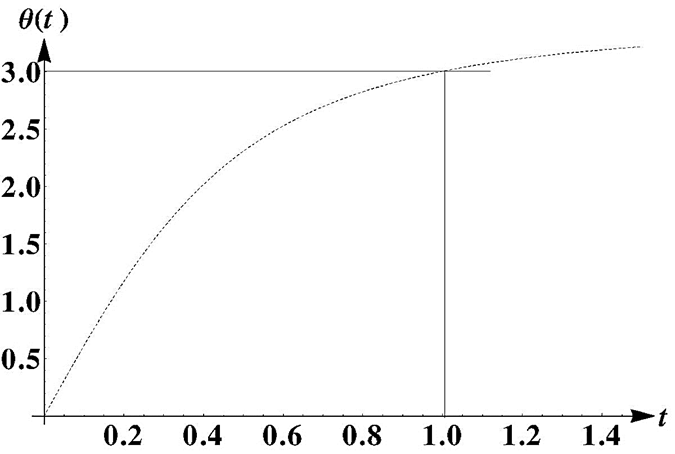
Figure 2 Trayectory of the pendulum for a maximum angle θ₀ = 171.9° = 3.0 rad. It can be noted that θ₀ is reached at t₀ = 1 sec and that the angular velocity does not vanish at t₀. 

The frequency compared with the frequency of the small angle limit w0=g/l is:

For the maximum time t₀ ≃1 sec for θ₀ = 171.9°, the ratio w/w₀ ≃ 0.502. If we compare this result with the exact solution w_exact/w₀ ≃ 0.4 and with the one obtained by using Belendez technique´ w_B/w_o ≃ 0.418 ⁸, we notice that the present method fails. For other maximum angles the results are similar and far from the exact solutions (see Fig. 3). This means that the error of the Polynomial method is around the 20% and it does not represent a good approximation for such angles.

Figure 3 The polynominal method is far from the exact solution. 

The question now is to understand why if the polynomial coincides with the cosine function for practically all the trajectory (the difference begin at 2.4 rad and it is minimal for θ₀, see Fig. 1), the result is so different to the exact solution. The answer is the following: first, it has to be noticed that since the parameter b does not coincide with 1/θ02, the final velocity (at θ = θ₀) does not vanish and it represents around the 20% of the typical velocity during the true trajectory (v_Typ = 3 rad/sec); second, the reason is inherent to energy conservation. A slight deviation can result in a significant difference. Indeed, the intersection between the horizontal line, the total energy E (see Fig. 4), and the exact potential energy, −mglcosθ, is achieved at θ = θ₀. However, the intersection between the horizontal line and the approximate potential energy, −mgl [(1 − cosθ₀)(1 − bθ²)³ + cosθ₀] with b = 0.085, is achieved at an angle bigger than θ_o (see Fig. 4). Moreover, the angle is bigger than π. Therefore, at θ = θ₀, the approximate potential has not reached the horizontal line which represents the total energy E. Consequently, the velocity does not vanish, θ₀ does not represent the turning point and the period is increased.

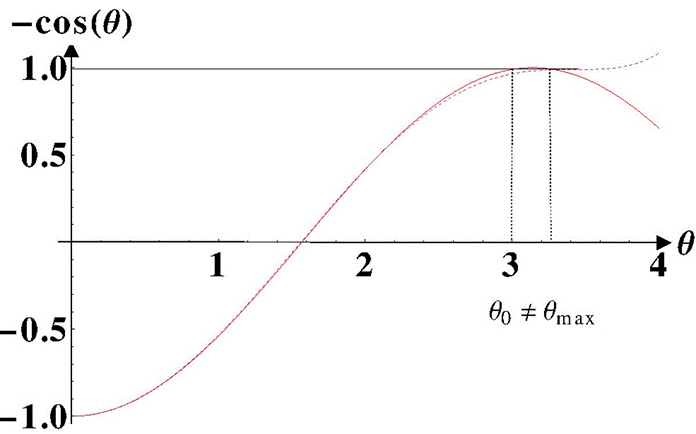
Figure 4 The minus cosine function is the continuous line; the approximate polynomial - [(1−cosθ₀)(1+bθ₀)³] with b = 0.085 is the dashed line. The approximate potential attains the total energy E at angle θ_max bigger than θ₀ 

The physical problem consists of noticing that the conservation of the energy is an essential issue in a method which pretends to give numerical solutions by means of an approximate function of the potential energy. Indeed, in a situation of one dimension by using the conservation of the energy, we can express the velocity at any moment as:

The energy can be expressed as the value of the potential energy at the maximum point; that is:

This means that the velocity obviously vanishes at this point. However, when the energy potential is approximated by another function U_app which does not equal exactly the energy at the critical point, the velocity of the particle does not vanish and consequently the method fails. It is necessary to minimize the error at this point. Therefore, we need to propose another method. In first instance, in order to obligate the angular velocity to vanish at the maximum angle θ₀, see Eq. (10), we can use a polynomial such that b=1/θ02. However, by doing this the polynomial is very different from the cosine function (see Fig. 5). The results will be highly deviated from the exact. Moreover, by looking at Eq. (8) the maximum time will diverge and the period will be infinite.

Figure 5 The Polynominal cosθ ≃ (1−cosθ₀)(1−bθ²)³+cosθ₀ with b = 1/θ². 

3. The Modified Polynomial

The conclusion of the above section consists of noticing that the polynomial has to be changed to another more complicated. The proposal is the following

where a new parameter c has been introduced. First of all, we can begin by obligating the polynomial to coincide with the cosine function at θ = θ₀ by putting

The resulting polynomial is also very different of the cosine function for all the other value of the angle. Therefore, it is necessary to fit the parameters b and c such that the polynomial completely matches the cosine function as possible for all the angles between θ = 0 and θ = θ₀ (see Fig. 6). This is achieved by calculating the standard deviation and by minimizing it as function of b and c, even if the value of the polynomial does not coincide with the cosine function at θ = θ₀. With the new adjusted parameters, we can continue with the procedure. Substituting Eq. (16), obtains

Integrating, arrives

The velocity at the maximum angle can be deduced by using

Finally, by obtaining the physical solution, we arrive at

with

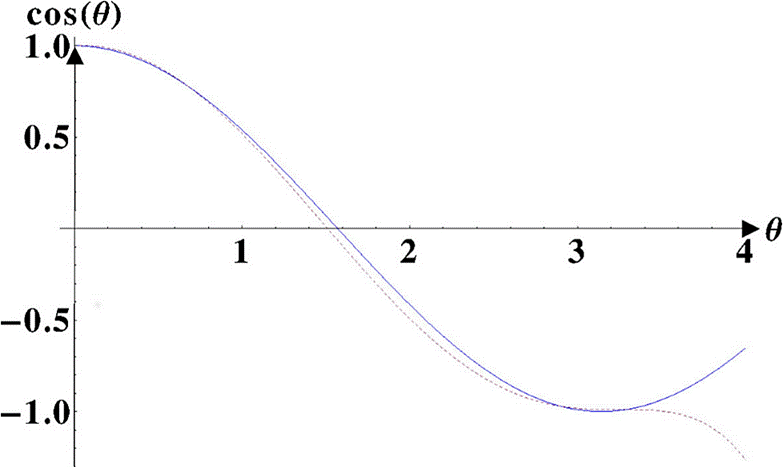
Figure 6 The modified polynomial is the dashed line; the continuous line is the cosine function; θ₀ = 171.9°, b = 0 : 097 and c = −0.009. 

By using Eq. (20), the velocities for the different maximal angles can be obtained; the maximal time for each maximal angle is graphically deduced (see Figs. 7, 8 and 9, where l = 1 m, g = 9.8 m/sec²). The frequency compared with the frequency of the small angle limit w₀ is

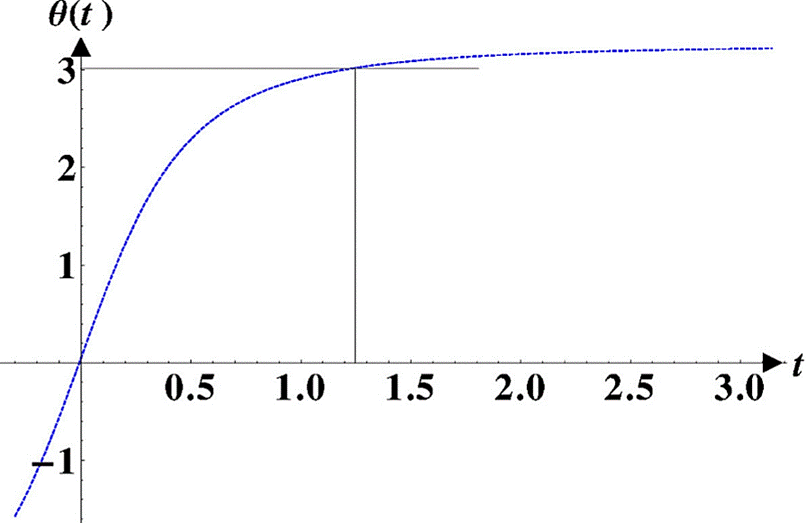
Figure 7 The trajectory for θ₀ = 171.9° with b = 0.097 and c = 0.009. The corresponding time t₀ ≃ 1.24 sec. 

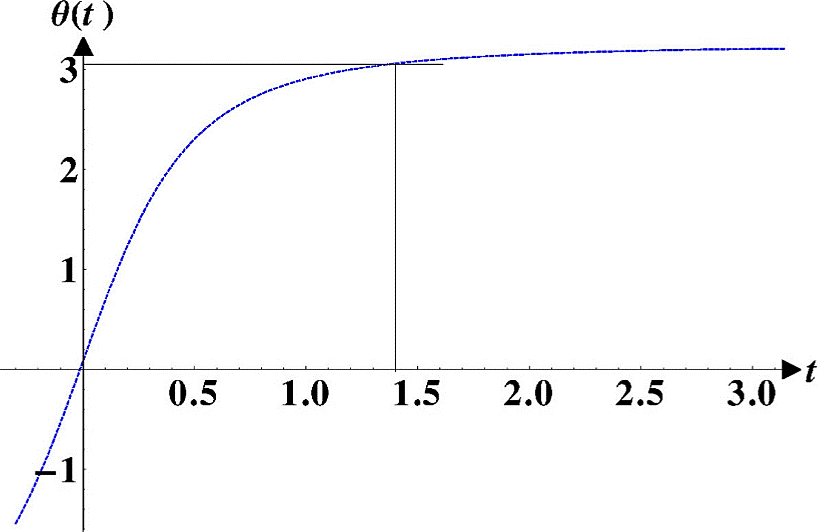
Figure 8 The trajectory for θ = 174.2° with b = 0.97 and c = 0.015. The corresponding time t₀ ≃ 1.4 sec. 

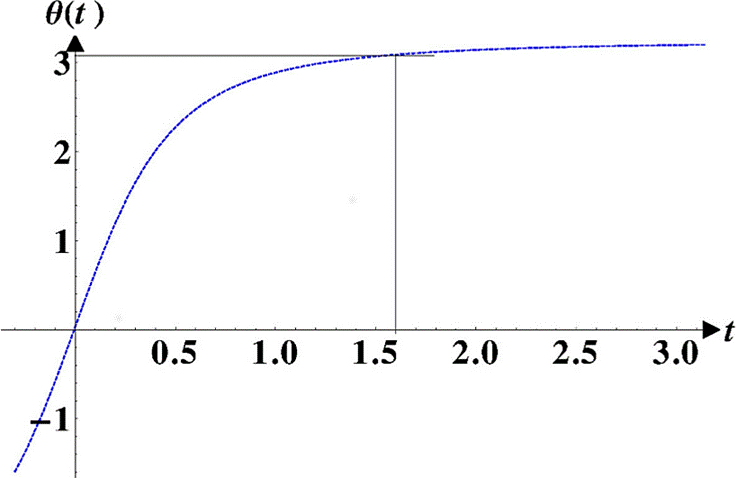
Figure 9 The trajectory for θ₀ = 177.4° with b = 0.097 and c = 0.013. The corresponding time t₀ ≃ 1.6 sec. 

We obtain by simple inspection of the trajectories in Figs. 7, 8 and 9 or by using Eq. (19), the times t₀ for θ₀ = 171.9°, θ₀ = 174.2°, and θ₀ = 177.4°. The corresponding angular velocities at θ = θ₀ by using Eq. (20). Once we have the maximal times, we can proceed to calculate the compared frequencies (see Table I) and in Fig. 10 we can observe that the frequencies are very close to the exact solutions and coincide for maximal angles close to π.

Figure 10 The modified polynomial method gives results that are between Belendez method and the exact solution. For higher´ angles the method converges to the exact solution. 

4. Concluding Remarks

We find a rapid method for obtaining the period of the simple pendulum just by using a polynomial method. Although the paths are not as good for angles near 170° since the velocity θ = 0.45 for θ₀ = 171.9°, for bigger angles the angular velocity practically vanishes, θ = 0.012 for θ₀ = 177.4° (the velocity is around 0.4% of the typical velocity), and the trajectories and the periods coincides with the exact solutions. It has to be highlighted that the method shows that a small deviation can lead to significant errors, where the conservation of the energy plays an important role.

Although the aim of the article was to find a method to know the periods of the motion of a simple pendulum for angles close to 180°, a goal that was fulfilled, actually the most interesting result is to understand that, at critical points, the approximate potential energies must match with real potential energies along all the trajectory. In fact, the use of a slightly more complicated polynomial allows that the approximate potential energy is as close as possible to the real potential value at the critical point and at the same time having a minimal standard deviation. The conservation of the energy and the nonlinear characteristic of the problem are the causes of such behavior.