Introducción
Ciudad Juárez, Chihuahua, México, es la ciudad que cuenta con la mayor producción de arneses para el sector automotriz en todo el mundo, por lo cual se le considera la capital mundial arnesera. Las operaciones de manufactura clave que se diseñan para la elaboración de un arnés son: corte de cable, desforre, crimpado, moldeo, soldadura, encintado, entre otras. Las operaciones de soldadura generalmente son consideradas críticas, siendo la soldadura ultrasónica la que sistemáticamente produce mayor cantidad de problemas dentro del proceso.
El presente proyecto se realiza en una de las mayores plantas arneseras automotrices de Ciudad Juárez, cuyos clientes principales son compañías como Ford, Chrysler, GM, Honda, Toyota, entre otras. Se plantea como propósito general el mejoramiento en la resistencia a la tensión de piezas soldadas, debido a que este es el que origina mayores costos de desperdicio y retrabajos en el proceso.
Dentro del proceso de soldadura, el principal problema que se identifica se encuentra en el cambio de la herramienta utilizada, mejor conocida como Anvil, la cual debe ser retirada para rectificación antes de que comience a generar piezas con baja resistencia a la tensión y por lo tanto defectuosas. Este documento describe una metodología y las bases para implementar el mantenimiento predictivo en la operación de soldadura ultrasónica.
En este trabajo se considera el uso de técnicas de probabilidad y estadística, especialmente las redes bayesianas, que actualmente tienen un auge importante dentro de la investigación. Por ejemplo, Straub y Der Kiureghian (2012) hacen una combinación de redes bayesianas y métodos de confiabilidad estructural para crear un nuevo marco computacional, denominado red bayesiana mejorada (eBN), para el análisis de confiabilidad y riesgo de estructuras e infraestructuras de ingeniería. Por otra parte, Zhang, Qin, Jiang y Huang (2018) proponen un modelo de análisis probabilístico para una red de oleoductos basado en las redes bayesianas con la finalidad de realizar un análisis sensible de accidentes. Mientras que Kraisangka y Druzdzel (2018) proporcionan un método para codificar el conocimiento de los modelos de riesgos proporcionales de Cox (CPH, por sus siglas en inglés) existentes para redes bayesianas, y concluyen que estas redes interpretadas a partir del modelo CPH pueden ser más útiles en la práctica que la estimación Kaplan-Meier o a las redes bayesianas aprendidas de los datos. Los resultados que aquí se presentan respaldan lo anterior, puesto que la aplicación de redes bayesianas-CPH resultó exitosa en el proceso de soldadura al generar ahorros por la cantidad de 270 000 dólares.
Materiales y métodos
La metodología descrita en este documento implica primeramente la obtención de datos del proceso de soldadura resultantes de la prueba de jalón (prueba destructiva) mediante un dinamómetro, cuyo sistema de medición se ha verificado previamente mediante un análisis de repetibilidad y reproducibilidad (R&R). Los datos fueron procesados para obtener su función de densidad de probabilidad: la distribución Weibull fue la de mejor ajuste.
El siguiente paso fue determinar los factores significantes en la resistencia a la tensión de las partes soldadas. Para ello se diseñó un experimento considerando los factores más importantes del proceso de soldadura, los cuales son: energía, presión y amplitud. Se trató de un experimento con tres factores en siete niveles cada uno (73), el cual fue corrido y analizado sin considerar interacciones.
Posteriormente, se diseñó una red bayesiana para el análisis que permitió hacer mejores inferencias y como consecuencia mejorar significativamente el proceso de soldadura. La mejora que se considera más importante fue determinar el tiempo de cambio de la herramienta (Anvil), gracias a lo cual fue posible anticiparse a la falla, es decir, que aparecieran piezas con baja resistencia al jalón. La intención principal del proyecto fue determinar la distribución de falla de la resistencia a la tensión de las piezas soldadas y relacionar esta con los factores significantes del proceso, para posteriormente analizar y mejorar el proceso mediante controles establecidos, y con ello, finalmente, determinar el tiempo de cambio de los electrodos de soldadura.
Marco teórico
Kraisangka y Druzdzel (2018) y Allison (2010) mencionan que el análisis de supervivencia es un conjunto de métodos estadísticos que auxilian en el modelado de las relaciones entre un conjunto de variables predictores y una variable de salida, además de ayudar a pronosticar cuándo un evento ocurrirá. Cai, Liu, Liu, Chang y Jiang (2020) consideran que la confiabilidad es la probabilidad de que un artículo desempeñe su función requerida bajo las condiciones de operación dadas para un intervalo de tiempo establecido. Cabe señalar, además, que esta puede ser evaluada usando técnicas de inferencia estadística apropiadas, tales como árbol de fallas, diagramas de bloques de confiabilidad, modelos de Markov, método de Montecarlo vía cadenas de Markov (MCMC, por sus siglas en inglés), metodología de superficies de respuesta, métodos de confiabilidad de primer orden y redes bayesianas.
Redes bayesianas
Las redes bayesianas son una herramienta de modelado gráfico que permite especificar las distribuciones de probabilidad de un conjunto de variables relacionadas entre sí que pueden representar una situación específica (Bermejo, 2019). Una red bayesiana es un medio de representación que tiene como objetivo organizar el conocimiento de una situación particular en un coherente “todo”.
Existen tres métodos principales que se utilizan para la modelación de situaciones mediante redes bayesianas. El primer método es mayormente subjetivo, pues refleja el conocimiento propio y el de otros en la red. El segundo sintetiza el conocimiento de otro tipo de conocimiento formal. Estos dos métodos mencionados anteriormente son conocidos como aproximación de la representación del conocimiento (KR, por sus siglas en inglés). El tercer método está basado en aprender las redes a partir de datos, tales como datos de confiabilidad humana, confiabilidad de software, diagnósticos médicos, entre otros.
En la época actual, las redes bayesianas han sido usadas para representar modelos en diferentes campos, principalmente en aquellos que presentan cierto grado de incertidumbre. Esto es: las redes bayesianas son modelos gráficos acíclicos dirigidos (DAG, por sus siglas en inglés) probabilísticos que pueden ser utilizados para el análisis de la incertidumbre. Cai et al. (2020), Khorshidi, Gunawan y Ibrahim (2016) y Darwiche (2009) proponen la siguiente definición de red bayesiana:
Una red bayesiana para variables Z es un par
G es un DAG sobre las variables Z, llamada la estructura de la red.
Ѳ es un conjunto de tablas de probabilidad condicional (CPT, por sus siglas en inglés), una para cada variable en Z, llamada la parametrización de la red.
El conjunto
Cai et al. (2020) establecen que las redes bayesianas usan nodos para representar variables y arcos para representar dependencias directas significantes entre los nodos unidos, además de probabilidades condicionales para cuantificar las dependencias.
Consideremos n variables aleatorias X
1
,X
2
,…,X
n
y un DAG con n nodos, donde el nodo
Ahí, pa(X j ) denota el conjunto de todas las variables X j y un arco conectará al nodo i con el nodo j en el gráfico.
Ahora, sea una red bayesiana con vértices X = {X 1 ,X 2 ,…,X n }. Entonces especifica una distribución de probabilidad conjunta única P(X) dada por todas las CPT especificadas en la misma red bayesiana.
Usando la regla de la cadena y los supuestos de independencia condicional, se pueden calcular las probabilidades conjuntas de las variables U = {X 1 ,X 2 ,…,X n } mediante:
Es decir, los productos de las probabilidades condicionales de X i y sus padres.
Enseguida se muestra un conjunto de códigos para la construcción gráfica de la red bayesiana una vez determinadas las variables (nodos) y sus relaciones (arcos). La Figura 1 muestra el resultado del código de acuerdo con el paquete bnlearn de R (Scutari, 2010).
library (igraph, warn.conflicts = FALSE)
gr2 <- graph (c(1,6, 2,6, 3,6, 4,6, 5,6))
plot (gr2, vertex.label = c('pres', 'temp', 'vel', 'tie', 'tipo', 'vida'),
layout = matrix (c(-15,200, -5,650, 0,1000, 5,650, 15,200, 0,0), byrow = TRUE, ncol = 2),
vertex .size = 30, vertex.color = 'red', vertex.label.cex = 1,
vertex.label.color = 'blue', vertex.frame.color = 'black', asp = 0.5, edge.arrow.size = 1)
Modelo de riesgo proporcional de Cox
De acuerdo con Kraisangka y Druzdzel (2018), el modelo de CPH es una de las técnicas que más popularidad tiene en el análisis de supervivencia. El modelo de CPH se puede comparar a una técnica de regresión lineal múltiple en la que se analiza la relación entre el riesgo y las variables explicativas relacionadas durante un período de tiempo. El análisis de supervivencia se enfoca principalmente en modelar las ocurrencias del tiempo transcurrido hasta que se presenta el evento.
La probabilidad de supervivencia de un dispositivo, después un tiempo determinado t, o bien la función de supervivencia se define como:
S(t) = PR(T > t) (1)
En este caso, T es una variable que representa el momento en que ocurre un evento de interés. La probabilidad de supervivencia de inicio, representada por t 0 , puede ser igual a uno o alguna probabilidad de supervivencia de línea base, la cual descenderá a cero con el tiempo.
La función de riesgo está dada por:
T es una variable de tiempo que representa el riesgo de que ocurra un evento en el tiempo
La relación entre la tasa de riesgo y la función de supervivencia se describe a continuación:
O bien:
La ecuación 4 muestra que se puede calcular la función de supervivencia a partir de la función de riesgo. La función acumulada de falla y la función de supervivencia son funciones complementarias. Por lo tanto:
En el análisis de supervivencia, la función de riesgo se puede representar mediante cualquier distribución de probabilidad, o se puede modelar mediante técnicas de regresión. El modelo CPH brinda una evaluación de la supervivencia basada en factores de riesgo que están asociados con los eventos indicados en el modelo. Un modelo CPH simple consiste en factores de riesgo independientes del tiempo. La función de riesgo en un modelo CPH se expresa como:
El modelo de riesgo se compone de principalmente de dos partes: la función de riesgo base
La función de riesgo base determina las amenazas en un nivel fundamental de las variables explicativas, por ejemplo, cuando los factores de riesgo están ausentes.
La función de riesgo denota que el riesgo para el individuo i en el tiempo t es el producto de dos factores (Allison, 2010):
Una función λ0(t) que no se especifica, excepto que no puede ser negativa.
Una función lineal de un conjunto de k covariables fijas, que luego se exponencia.
La función
Tomando el logaritmo de ambos lados, podemos reescribir el modelo como:
Si
Ahora, si tomamos la razón de riesgo para dos individuos
Con esto se obtiene la proporción de riesgos constante en el tiempo; a esta ecuación se le llama modelo de riesgos proporcionales. Este modelo tiene como característica que, al graficar el logaritmo para cada uno de los individuos, dichas funciones de riesgo deben ser estrictamente paralelas (Figura 2).
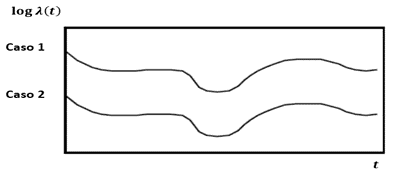
Fuente: Allison (2010)
Figura 2 Funciones paralelas de Log Riesgo del modelo de riesgos proporcionales
Función de verosimilitud parcial
En el modelo de regresión de Cox los parámetros
Esta función considera solo las probabilidades de los tiempos de falla, y no las de tiempo de datos censurados.
Esto suponiendo que tenemos
Resultados
El proyecto se desarrolló en una planta fabricante de arneses en Ciudad Juárez, donde específicamente se seleccionó un arnés de batería, el cual presentaba problemas de desprendimiento al realizar la prueba de jalón efectuada a la salida del proceso de soldadura ultrasónica. La Tabla 1 muestra los resultados de la prueba de jalón efectuada durante un periodo de tiempo establecido. Al analizar los datos, se encontró que el comportamiento (función de densidad de probabilidad) era de acuerdo con una distribución Weibull (véase la Figura 3).
Construcción del modelo CPH
Tabla 1 Datos de resistencia a la tensión a las condiciones de trabajo actuales
|
|
|
|
|
|
|
Fuente: Elaboración propia
Diseño de experimentos
Para comprobar la significancia de los factores se diseñó un experimento con tres factores en siete niveles cada uno (73). Se corrieron las 343 combinaciones del diseño. Los niveles se tomaron de pruebas realizadas y de la bitácora de los técnicos, cuya experiencia indicaba que podían soldarse piezas que cumplieran con la especificación mínima. Los factores y sus niveles se muestran en la Tabla 2.
Tabla 2 Factores y niveles del diseño de experimentos.
| Factor | Niveles | Valores | ||||||
| Presión | 7 | 2.65 | 2.67 | 2.70 | 2.73 | 2.76 | 2.79 | 2.81 |
| Amplitud | 7 | 0.58 | 0.64 | 0.71 | 0.77 | 0.84 | 0.90 | 0.97 |
| Energía | 7 | 154 | 786 | 1419 | 2051 | 2684 | 3317 | 3950 |
Fuente: Elaboración propia
En el análisis de los resultados, se eliminaron todas las interacciones posibles de dos y tres factores. Los resultados se muestran en la Tabla 3 con el análisis de varianzas.
Como se observa en la tabla, los tres factores, presión, amplitud y energía, resultaron significantes (p-value < 0.05). En la Figura 4 se muestran las gráficas factoriales donde se observa que los niveles recomendados fueron: presión = 0.81, amplitud = 0.97 y energía = 3950.
En lo siguiente se muestra el código R para la construcción de la red bayesiana de los factores significantes y la red bayesiana resultante (Figura 5).
library(igraph, warn.conflicts = FALSE)
gr1 <- graph(c(1,5, 2,5, 3,5, 4,5))
plot(gr1, vertex.label = c('T', 'Presión', 'Amplitud', 'Energía', 'Vida'), layout = matrix(c(-40,650, -20,1000, 20,1000, 40,650, 0,0), byrow = TRUE, ncol = 2), vertex.size = 70, vertex.color = 'blue', vertex.label.cex = 1, vertex.label.color = 'black', vertex.frame.color = 'black', asp = 1.5, edge.arrow.size = 0.75)
En la Tabla 4 se pueden observar los valores más altos de tasa de riesgo de la energía, presión y amplitud, así como los niveles de cada uno de ellos. Asimismo, se muestran los valores altos de supervivencia en cada uno de los niveles de los diferentes factores. Un resultado de gran importancia, el cual fue la principal motivación para la realización de las actividades antes mencionadas.
Tabla 4 Factores de riesgo y sus niveles: tasas de riesgo, razones de riesgo y supervivencia
| Factor de riesgo | Nivel 1 | Nivel 2 | Nivel 3 | Nivel 4 | Nivel 5 | Nivel 6 | Nivel 7 |
| Energía | 154 | 786 | 1419 | 2051 | 2684 | 3817 | 3950 |
| Tasa de riesgo λ | 0.0143 | 0.016 | 0.00229 | 0.0103 | 0.00563 | 0.0025 | 0.00241 |
| Razón de riesgo γ | 347 | 400 | 56 | 251 | 137 | 61 | 58 |
| Supervivencia (S) | 0.0306 | 0.018 | 0.5699 | 0.080 | 0.2524 | 0.542 | 0.5544 |
| Presión | 2.65 | 2.67 | 2.70 | 2.73 | 2.76 | 2.79 | 2.81 |
| Tasa de riesgo λ | 0.0045 | 0.1015 | 0.0075 | 0.00293 | 0.00219 | 0.001129 | 0.00908 |
| Razón de riego γ | 112 | 247 | 182 | 71 | 53 | 28 | 22 |
| Supervivencia (S) | 0.3228 | 0.0835 | 0.1509 | 0.4879 | 0.1590 | 0.7583 | 0.8001 |
| Amplitud | 0.53 | 0.64 | 0.71 | 0.77 | 0.84 | 0.90 | 0.97 |
| Tasa de riesgo λ | 0.00238 | 0.00608 | 0.00745 | 0.0069 | 0.0019 | 0.003313 | 0.00254 |
| Razón de riesgo γ | 58 | 148 | 182 | 168 | 46 | 49 | 62 |
| Supervivencia (S) | 0.558 | 0.2253 | 0.1609 | 0.1838 | 0.6280 | 0.6220 | 0.3360 |
Fuente: Elaboración propia
Discusión
La industria ensambladora en México, principalmente la automotriz, se ha convertido en una de las principales fuentes de divisas en México. Que los productos de la industria maquiladora funcionen correctamente asegura, en primer lugar, la permanencia de la industria en el país. La mejor forma de lograr lo anterior es mediante la utilización de herramientas estadísticas consideradas dentro de la ingeniería de confiabilidad, como el análisis de confiabilidad, la ingeniería de mantenibilidad y el análisis de degradación. De acuerdo con Marjanović, Kvaščev, Tadić y Đurović (2011), la confiabilidad de los sistemas es uno de los principales problemas en la industria actual, por lo que el desarrollo de técnicas avanzadas de mantenimiento del sistema es una tarea relevante. Uno de los aspectos que se evalúan dentro del mantenimiento es el desgaste de los elementos que configuran un mecanismo, lo que implica no solo detectar piezas que provocan el paro de los equipos, sino analizar el comportamiento de su degradación.
El análisis de degradación consiste en verificar, de una manera continua, la función específica de la operación para determinar el cambio del comportamiento, y relacionar el cambio con las herramientas que presentan desgaste, lo que permite determinar la necesidad de un cambio o de una rectificación. El análisis de la degradación podría conducir a la obtención de una función de degradación, y determinando parámetros necesarios para la programación del mantenimiento, como el tiempo medio de reparación y los tiempos ideales para cambios de herramentales, principios básicos del mantenimiento predictivo, anticiparse a la falla. Existen otros métodos dentro de la literatura como el mantenimiento basado en condiciones que contribuye a reducir fallas inesperadas con mínimos costos, como lo mencionan Chen, Ye, Xiang y Zhang (2015), y que utiliza la información de la degradación, sin embargo, los resultados encontrados en esta investigación fueron relevantes en su aplicación y en los beneficios calculados.
El proyecto descrito en este documento arrojó un ahorro de 270 000 dólares, el cual se considera puede extenderse a un ahorro anual, solamente en esa operación, es decir, en esa línea de producción, una de las siete líneas similares que existen en la planta, en las cuales se inició el análisis siguiendo esta metodología.
Es importante aclarar que el éxito alcanzado del proyecto se debió, básicamente, al apoyo de la gerencia, en este caso el gerente de mejora continua, sin el cual no se hubiera logrado. Se menciona esto porque la falta de apoyo para la realización, que implica el tiempo de máquina, los recursos humanos, los materiales necesarios y el acceso a las instalaciones, son de los principales impedimentos que este tipo de proyectos tienen.
Conclusión
Los resultados obtenidos mediante la introducción de conceptos de mayor complejidad para el mejoramiento de procesos, tales como el modelo de CPH, el análisis de degradación, la inferencia bayesiana y el análisis mediante redes bayesianas, logran básicamente reducir la incertidumbre en las inferencias establecidas. También la introducción de un software programable permite un buen análisis de resultados, esto desde el punto de vista confiable, precisamente por la programación y la utilización de simulaciones mediante el método de MCMC cuando se utilizan redes bayesianas.
Los proyectos de este tipo en la industria generalmente arrojan excelentes resultados, pero el problema más recurrente para la implementación de metodologías que requieren tiempo de máquina, materiales y recursos humanos es el apoyo de la administración, debido a que lo ven como pérdidas económicas y no, a través de una aplicación efectiva, como una forma de generar importantes ahorros a través del tiempo. Es por esto por lo que siempre es necesario realizar un análisis costo-beneficio para evaluar la factibilidad económica-financiera en este tipo de proyectos.
Futuras Líneas de investigación
El área de control de calidad, la ingeniería de confiabilidad y actualmente la inferencia bayesiana han generado una amplia gama de futuros proyectos para la mejora de productos y procesos. El área de la confiabilidad y la mantenibilidad ofrecen grandes oportunidades para el desarrollo de proyectos. Específicamente, el OEE = Disponibilidad x Rendimiento x Calidad es uno de los indicadores más importantes en las plantas manufactureras, y es posible mejorarlo utilizando los conceptos antes mencionados y aplicando las herramientas estadísticas que estas conllevan.
Un agradecimiento al Consejo Nacional de Ciencia y Tecnología por el apoyo brindado a través de becas nacionales en los estudios doctorales y posdoctorales.











 nueva página del texto (beta)
nueva página del texto (beta)








