1.Problem formulation and introduction
From several years to extract exact solutions of complex non- linear dynamical systems is one of the most excited and challenging areas of research for many mathematicians and researchers because of the high applicability of these equations arising in applied physics and mathematical studies to explain nonlinear wave phenomena. Complex nonlinear partial differential equations (CNLPDEs) are highly applicable in many technical, natural, and scientific sciences, which are mathematical physics, electromagnetism, biomedical problems, telecommunication networks based on optical fiber technology, chemistry, nuclear physics, solid state physics, plasma physics, optics and in many other engineering subjects 1-34. Optical solitons appearing in optical physics and plasma physics particularly have a significant role in the improvement of new theories of applied physics. Moreover, the development of new reliable, simplified, and very efficient analytical methods for finding optical solitons is a challenging field of research, especially in those areas where the existence of optical solitons is frequently experienced, including nuclear physics and in some other sub-areas of applied physics. So the motivation of present research work is to study those analytical methods which are highly helpful with sufficient computational reliability of time and very efficient in calculations for the computation of optical solitons appearing in optical physics, plasma physics, quantum physics, nuclear physics, mathematical physics and in many other sub- fields of natural sciences. So the goal of our work is the presentation of analytical analysis of nonlinear perturbed fractional Schrödinger equation using Kerr law type nonlinearity by our introduced method EMAEMM.
In recent years internet and various other telecommunication networks are the basic components to transfer information data. In this process, technology based on optical fiber’s medium is the backbone of a transformation of information from here and there which has potential applications in the development of bio-mathematical studies. Due to high impact applications of optical solitons, which are counted as basic components of information transfer so, it is very important to study those methods which are more reliable with less computational time for the computation of optical solitons. So the present work is focused to introduce a new technique with only three parameters to extract optical solitons. The theory of fractional calculus starts from Grunwald, Liouville, Leibniz, Riemann, and Letnikov plays an important and very remarkable role in many applications of physics, biology, viscoelasticity, engineering, finance, control theory, fractional dynamics, signal processing, and many other branches of sciences 2.
Nowadays, the analytical study of nonlinear fractional partial differential equations has attained the great attention of both physicists and mathematicians. Many researchers have widely study integrable nonlinear perturbed fractional Schrödinger Equation using Kerr law type nonlinearity introduced by Nick Laskin, a well known governing model appearing in quantum mechanics and optical physics with potential applications 3. Many researchers have used numerical methods to obtain its approximated solutions, but our work is motivated to present the analytical treatment of this governing model via our newly introduced technique by implementation, we found a variety of more general and new families of analytical results in a compact form 4,5. So our research work is based to extract optical solitons for PNLFSE. By using our new technique, some new and more varieties of analytical solutions in more general forms have been founded by us, which includes semi half-bright, semi half dark, bright, dark, half dark, combined, periodic, half periodic, half-bright, doubly periodic with the usage of three parameters which is the main different point of our new technique. These calculated results have a highly positive impact on the improvement of theoretical plasma physics, biomedical problems, optical physics, electromagnetism, industrial physics, soliton dynamics, nuclear physics, telecommunication networks, mathematical physics, and in some other sub- fields of physical sciences. Also, some necessary and sufficient constraint conditions are evaluated during the mathematical derivation of extraction of optical solitons.
Several techniques in the literature are developed using different mathematical software for the analytical analysis of nonlinear fractional partial differential equations. Such as the Jacobi elliptic function technique 6, Kudryashov technique, extended Fan sub-equation technique 7,8, the Bäcklun transform technique 9,10, homogenous balance technique 11, the truncated expansion technique 12,20, the tanh-function technique 21, inverse scattering technique 22,23 and many more.
A brief introduction of the perturbed nonlinear fractional Schrödinger equation has been presented in section first by using Kerr law nonlinearity. A detailed explanation of the algorithm of the developed method is presented in section second. Implementation of the method has been presented in section third for the extraction of exact solitons of nonlinear fractional perturbed Schrödinger equation to check computational efficiency and reliability of the technique. Section fourth is the representation of graphs of obtained solutions. In section five discussion of the results with some important concluding remarks has been presented.
2.Summary of the extended modified auxiliary equation mapping method
Firstly we assume that we are having generally a nonlinear partial differential equation(NLPDE) which is presenting any nonlinear wave phenomena with the association of a set of independent variables T y = {y 0 = t, y 1 , y 2 , ................, y p } of independent variables for dependent function φ(y, t) followed in the following manner
where S is the representation of a general polynomial function having its complex argument function φ(y, t) with associated partial derivatives and its nonlinear terms.
For the computation of exact traveling required results, we will use the below-mentioned linear traveling wave transformation.
Here Ω i , i = 0, 1, ............M, . are constants which can have any value and will be calculated later. Further substituting above mentioned transformation (2) into (1) yields the given below
the nonlinear ordinary differential equation (NLODE), while F is the representation of a polynomial in φ(ξ) with associated its total derivatives φ´ , φ´´ , φ´´´ , ................... etc. Further we will consider that φ(ξ) satisfies the general solution in the series form of θ(ξ),
In the above general solution, d j c j b j a j are all arbitrary constants which will be calculated later, and θ(ξ) satisfies the below-mentioned derivative in three parametric values:
While π 1, π 2, and π 3 are any type of constants that will be evaluated later. To calculate φ(ξ) explicitly, we will follow the below-mentioned steps:
First step: we need to determine the value of non- negative integer ”m” by making a quite balance be- tween the highest order non-linearity terms and the terms of highest order partial derivative in Eq. (3).
Secondly: substitute the general solution (4) along with Eq. (5) into Eq. (3) nonlinear ordinary differential equation, and considering the collection of all these coefficients to zero, we will obtain a set of algebraic type equations, and then further with the help of any suitable mathematical solver like Maple, Mathematica, Matlab, after that some sets of values of constants will be obtained d j , c j , b j , a j .
Finally, by using all those values of constants which we determined above into the general solution (4) then we will get the solutions of (1) which are required.
3.Nonlinear perturbed fractional Schrödinger equation using Kerr law type nonlinearity
Here we are going to apply our introduced technique for the extraction of new optical solitons of integrable nonlinear perturbed fractional Schrödinger equation using Kerr law type nonlinearity 3, which is frequently appeared in the area of plasma physics, optical physics, theoretical physics, and quantum mechanics mentioned below in dimensionless form 3.
Here in Eq. (6), v(x, t) shows complex wave profile while the term (∂ β v/∂ t β ) shows the fractional derivative in the meaning of modified Riemann-Liouville derivatives, for the detailed description see 2, and γ i , i = 1, 2, 3. are the co- efficients of dispersion, particularly γ 1 is known as 3rd order dispersion, γ 2 shows nonlinear dispersion, and γ 3 also shows some kind of nonlinear dispersion. To solve the above (6) governing model, consider the following initial wave transformation
where b and a are arbitrary constants. By putting (7) into (6), we get the nonlinear ordinary differential equation (NLODE) mentioned below.
Here c is an arbitrary constant while χ(ξ) is a real function.
Then (8) takes the form as
By breaking real and imaginary parts in (10) respectively, we obtained
Through integration (12) and putting constant of integration equal to zero for simplicity, so we got the below- mentioned equation
By (11) and (13), we obtain the following equation
From (14), we obtain the following
Here R 1 = b 2 − 3γ 1 b 3 c, R 2 = −ac − b 2 c 2 + γ 1 b 3 c 3 and R 3 = γ − γ 2 bc. So finally Eq. (11) together with the Eq.(12) takes the following form:
After applying homogeneous principal between the terms χ 3 and χ´´ in Eq. (16), we obtain n = 1 then further via proposed method Eq. (16) is considered to have a general solution in the form of a series given as:
Here above ψ(η) satisfies the equations of its partial derivatives:
By putting Eq. (17) along with (18) into Eq. (16), and considering the collection of all those coefficients ψ´ k (ξ)ψ j (ξ) ( k = 0, 1 j = 0, 1, 2, 3, 4, 5, .......n, ) of same powers and by setting all these coefficients equal to zero, we will obtain a set of algebraic type equations, and then further using any suitable mathematical solver, for example, Maple, Matlab, Mathematica different new families of analytic solutions in a more general form associated with different values of constants a 0 , a 1 , b 1 , d 1, and frequency are calculated, using them into Eq. (17) different new families of exact traveling wave results in a more general form of perturbed nonlinear fractional Schrödinger equation are listed below.
Family 1:
Next, using these values in Eq. (16) along with Eq. (18), so the solutions via the newly proposed method in this family of Eq. (6). are found in the following.
Where µ
1
> 0,
Where
Above ”
Where µ1 >0, (24)
Here ∆1 = (−ac − b 2 c 2 + b 3 c 3 γ 1), ∆2 = (γ − bcγ 2), ∆3 = (b 2 − 3b 2 cγ 1), here ”p” and ”ξ 0” represents any constant values.
Family 2:
Next, using these values in Eq. (16) along with Eq. (18), so the solutions via the newly proposed method in this family of Eq. (6). are found in the following.
where
where
Above ” ϵ” and ”δ” can have suitable values of −1 or 1.
ecuacion
Where µ1 > 0, (28)
Here ∆1 = (−ac − b2c2 + b3c3γ1), ∆2 = (γ − bcγ2), ∆3 = (b2 − 3b2cγ1), here “p” and “ξ0” represents any constant values.
Family 3:
Next, using these values into Eq. (16) along with Eq. (18), so the solutions via the newly proposed method in this family of Eq. (6). are found in the following.
where
where
Above 𝜖 and δ can have suitable values of −1 or 1.
where µ1 > 0, (32)
Here ∆1 = (−ac − b2c2 + b3c3γ1), ∆2 = (γ − bcγ2), ∆3 = (b2 − 3b2cγ1), here ”p” and ”ξ0” represents any constant values.
Family 4:
Next, using these values in Eq. (16) along with Eq. (18), so the solutions via the newly proposed method in this family of Eq. (6). are found in the following.
where
where
Above
Where
Here ∆1 = (−ac − b2c2 + b3c3γ1), ∆2 = (γ − bcγ2), ∆3 = (b2 − 3b2cγ1), here ”p” and ”ξ0” represents any constant values.
Family 5:
Next, using these values in Eq. (16) along with Eq. (18), so the solutions via the newly proposed method in this family of Eq. (6). are found in the following.
where
where
Above ”
Where µ1 > 0, (40)
Here ∆1 = (−ac − b2c2 + b3c3γ1), ∆2 = (γ − bcγ2), ∆3 = (b2 − 3b2cγ1), here ”p” and ”ξ0” represents any constant values.
4.Physical description of the solutions
This section is devoted to giving us the graphical representation of newly found results including some type of rational functions, trigonometric type functions, type of combined functions, hyperbolic functions in different forms to obtain a more clear picture of physical structures of perturbed nonlinear fractional Schrödinger Equation via Mathematica 10.4.
Results and discussion
Here we are going to list the similar and different points of our calculated new families of required results which we have been calculated using a newly developed method in comparison of all those solutions which are already present in the literature calculated by some old other analytical mathematical techniques for the same dynamical equation.
Firstly: The important and main differentiated point of our developed method to calculate new families of results is the unique structure of its body (4), which is totally new and unique structure using parametric values three only.
Secondly: To know about the clear picture of the dynamics of our newfound results their physical representations with the help of different sets of values of constants d j , c j , b j , a j are shown using mathematical solver like Matlab, Mathematica 10.4, or Maple (see Figs. (1-5)).
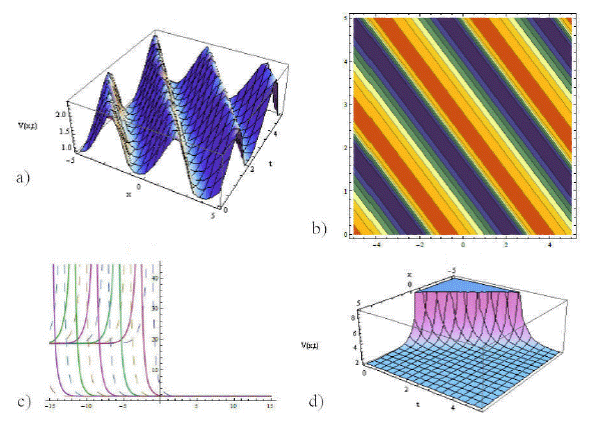
Figure 1 The graphs plotting of (23) and (24) is given. Here fig. a) is 3rd-dimensional graph of (23) as a periodic type soliton with associated values of parameters ξ0 = −3, 𝜖 = 1.9, a = −2,µ1 = −2, µ2 = −1.8, b = −1.6, c = −1.1, µ3 = 1.9 in intervals (0,5), (-5,5). And b) shows contour plotting of (23) considering all those parametric values used above in intervals (-5,5), (0,5). And c) represents the two-dimensional graph of (24) as semi half-bright type soliton using intervals (0,10), (-15,15). And d) represents 3rd- dimensional plotting of (24) with parametric values ξ0 = 1.8, 𝜖 = −1.8, µ1 = 3.0, µ2 = 1.8, a = 2.1, b = 1.6, c = 1.1, µ3 = −1.9 with in intervals (0,5), (-5,5).
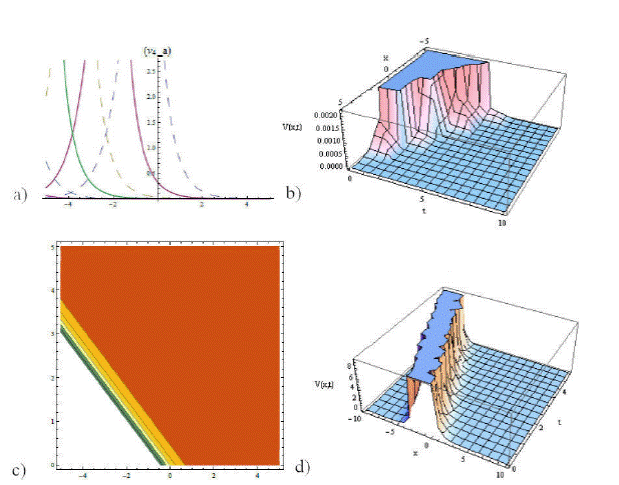
Figure 2 The graphical representation of (26), (27) and (28) is given in different dimension. Here a) visualizes the graphical representation of (26) with ξ0 = 1.33, 𝜖 = −1.9, a = −2.1,µ1 = 2.6, µ2 = 1.98, b = 1.6, c = 1.1, µ3 = 2.1 in intervals (0,5), (-5,5). And b) represents 3rd- dimensional plotting of (27) as semi half-bright type soliton using intervals (0,10), (-5,5). And c) shows contour plotting of (27) with the mentioned values of parameters using intervals (-5,5), (0,5). And d) presents 3rd-dimensional graphing of (28) soliton of bright type with ξ0 = 1, 𝜖 = 1.9, a = 2.1,µ1 = 2.5, µ2 = 1.6, b = −1.6, c = −1.1, µ3 = 2 using intervals (0,5), (-5,5).
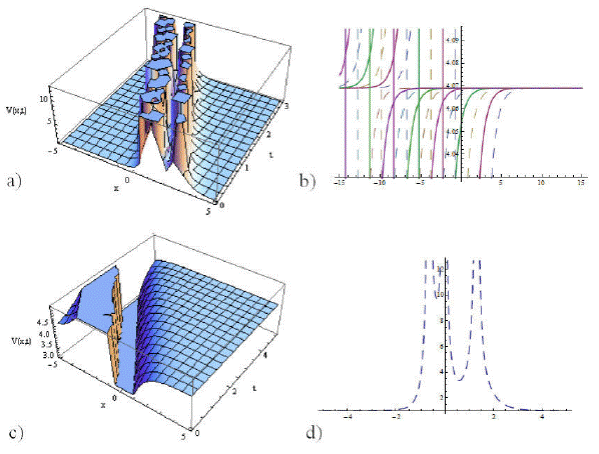
Figure 3 The physical representation of (31), and (32) has been given. Here a) visualizes the graphical figure of (31) as half doubly bright type soliton with ξ0 = −1.8, 𝜖 = −1.7, a = 2.9,µ1 = 1.6, µ2 = 1.9, b = −1.6, c = 1.1, µ3 = 1.988 in intervals (0,3), (-5,5). And b) shows 2nd-dimensional plotting of (32) as bright- dark (combined) soliton in intervals (0,10), (-15,15). And c) represents 3rd-dimensional plotting of (32) with ξ0 = 1.9, 𝜖 = −1.8, µ1 = 1.7, µ2 = −1.98, a = 2.1, b = 1.9, c = −1.98, µ3 = 2.8 in intervals (0,5), (-5,5). While d)shows the one dimensional graph of (31) considering all those parametric values used above in interval (-5,5).
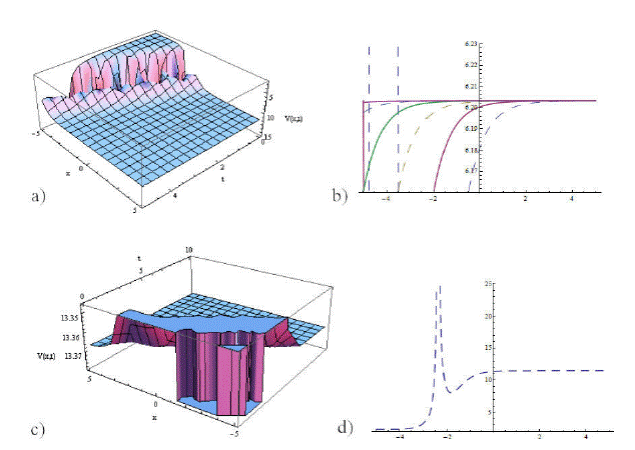
Figure 4 The physical plotting of (34), (35), and (36) has been given. Here a) visualizes the graphical representation of (34) as dark soliton with ξ0 = 1.6, 𝜖 = 1.6, a = −2.8, µ1 = 1.9, µ2 = 1.99, b = 3.1, c = −1.8, µ3 = 1.88 in intervals (0,5), (-5,5). And b) shows two dimensional graphical representation of (35) in intervals (0,5), (-5,5). And c) visualizes 3rd-dimensional plotting of (36) with ξ0 = 3, 𝜖 = 1.8,µ1 = 1.8, µ2 = 1.8, a = −2.1, b = −1.7, c = 1.8, µ3 = 2.9 in intervals (0,10), (-5,5). While d) shows the one dimensional graph of (34) considering all those parametric values used above above using interval (-5,5).
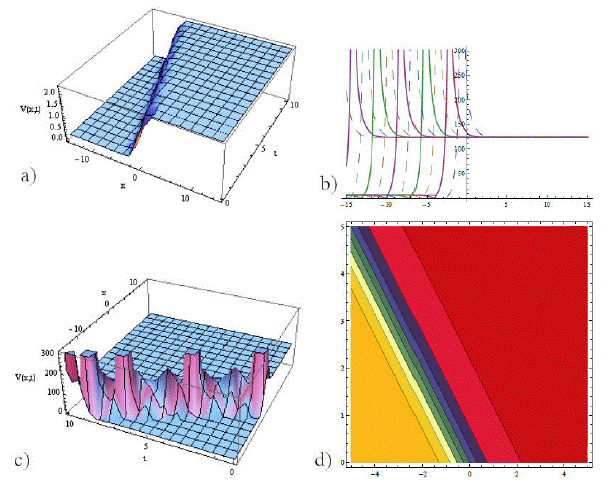
Figure 5 The physical representation of (39) and (40) has been given. Here a) visualizes the graphical representation of (39) as kink type soliton with ξ0 = 0.5, 𝜖 = 0.8, a = 3.9, b = 2.5, c = 0.5, µ1 = 0.8, µ2 = 3.9, µ3 = −3.99 in intervals (0,10), (-15,15). And b) represents 2nd-dimensional plotting of (40) as soliton of bright type using (0,10), (-15,15). And c) visualizes 3rd-dimensional plotting of (40) as bright type soliton in intervals (0,10), (-15,15). While d) shows contour plotting of (39) considering all those parametric values used above using intervals (-5,5), (0,5).
It is necessary to mention Eq. (5) showing us new different in more general forms of analytic solutions in different dimensions, including some type of rational functions, trigonometric functions, combined functions, and some type of hyperbolic functions.
Now we are going to list the differences of our calculated new families of required results which we have been calculated using a newly developed method in comparison of all those solutions which are already present in the literature calculated by some other different old analytical mathematical techniques for the same dynamical equation.
Comparing new found exact results with those obtained using technique Extended Fan-Sub Equation:
In Extended Fan-Sub Equation, the author Yomba 41 explained that when we consider parametric values h0 = 0 and h1 = 0, then under this consideration, the general elliptic equation will deform into sub-equation auxiliary ordinary differential equation further according this case, he listed all possible results for PNFSE (6) but the different point here in our presented research work we have found some new solutions in a more general form defined in complex domain for the same case as mentioned above which were missing in this case calculated in a simplified and straight forward way with in minimum computational time by one technique.
We have calculated a variety of new families of required results which are quite general and compact defined in a complex domain with the help of only one method, which depends on three parametric values for perturbed fractional nonlinear Schrödinger equation 41.
These newfound results are highly applicable in the improvement of theoretical studies of many other areas of natural sciences, including mathematical physics, plasma physics, biomathematics, nuclear physics, optical physics, quantum field theory, and in some engineering disciples.
All the solutions newly found here are also verified using mathematical solver Mathematica 10.4.
We would like to mention here that reliability, simplicity, straightforwardness, minimum computational time shows actually the high efficiency of our newly introduced method with the usage of only three parametric values in comparison to other methods.
Solutions found by First Integral Method:
we compared our solutions with those which are found by First Integral Method mentioned in 42 we noticed all listed results are defined with in real domain, while our solutions are quite new and different defined in complex domain.
Solutions found by Bernoulli Sub-ODE Method:
we compared our solutions with those which are found by the Bernoulli Sub-ODE Method listed in 42, we noticed all listed results are defined within a real do- main, while our solutions are quite new and differently defined in complex domain.
By concluding, it is important to mention that the solutions obtained in 41,42 are quite different in comparison of our required found results. Thus from the above comparative study, we can say in short, our developed technique gives us the results in less computational time with straightforward manner of high reliability and efficiency. Our new simplified solutions are highly helpful to show a clear picture about the analytical treatment of many other complicated dynamical systems appearing in other natural and physical sciences with the range of three parameters.
Concluding remarks
Our objective was to present a new method for the analytical analysis of many other nonlinear complex partial differential equations appearing in different areas, which are mathematical physics, telecommunication networks, plasma physics, quantum mechanics, biomathematics, nuclear physics, optical physics, quantum field theory, chemistry, telecommunication networks, nanotechnology and in some engineering
disciples. To check the efficiency of our developed technique we have applied on complex nonlinear perturbed fractional Schrödinger equation after implementation, we have calculated a verity of new analytical solutions in more general forms which are very useful to study many other nonlinear dynamical systems qualitatively, also they are highly useful in the improvement of theoretical plasma physics, biomedical problems, optical physics, electromagnetism, industrial physics, soliton dynamics, mathematical physics, telecommunication networks, nuclear physics and in other subfields of physical sciences. These calculated solutions have a profound impact to develop new mathematical solvers in the market, which are useful in the numerical analysis of complicated dynamical systems which are representing nonlinear wave phenomena. They are useful to present their comparison between analytical and numerical solutions. Moreover, graphical representation has been presented by us to show more clear picture of the dynamics of found new required results drawn using mathematical solver Mathematica 10.4.
It is important to highlight here that our developed technique gives us the results in less computational time with a straightforward manner of high reliability and efficiency. Our new simplified solutions are highly helpful to show a clear picture about the analytical treatment of other complicated dynamical systems with the range of three parameters appearing in other natural and physical sciences.











 nueva página del texto (beta)
nueva página del texto (beta)


