1. Introduction
In recent years, there has been a great interest in the process of pair creation by
strong electric fields after the pioneering works of Sauter [1], Heisenberg and Euler [2] and Schwinger [3]. Since then,
the pair creation of particles and antiparticles from the unstable vacuum by
external electromagnetic fields became a curious process in quantum electrodynamics
(QED).
In a seminal study [3], Schwinger exactly
calculated the pair creation probability from the vacuum due to an external field by
applying the proper-time formulation. He showed that the pure magnetic fields do not
produce any pairs of charged particles, but the presence of a magnetic field
modifies the probability of pair creation when the vacuum is perturbed by an
electric field. The probability of pair creation in a constant homogeneous electric
field is given by the Schwinger rate [4,5], namely,
P∝e-πEcE,
(1)
Where Ec=(m2c3/eℏ)≃1018 V/m is Schwinger’s critical field. This exponential is independent of
the spacetime variables and does not admit a Taylor expansion in e
or E, which indicates that this is a nonperturbative effect.
In addition, the theory of quantized fields in curved spacetime is one way of
unifying Einstein’s general relativity and quantum field theory in Minkowski
background. The mechanism of particle creation by the external electric field is
analogous to the particle production by a time-dependent metric of a curved
spacetime [6-9]. The cosmological particle creation mechanism in a time-dependent
gravitational field is one of the most remarkable known results. This mechanism has
an important role in explaining the origin of the structures in our Universe and
opened a new field in physics.
In order to study the process of particle creation in a timedependent gravitational
field, many different approaches have been developed such as the Hamiltonian
diagonalization method [10,11], path integral technique [12,13],
the Green function approach [14], the
semiclassical WKB approximation [15,16], the method based on vacuum-vacuum
transition amplitude [3], and the “in” and
“out” states formalism [17,18].
Recently, the particle creation problem under the influence of electromagnetic and/or
gravitational fields was studied in [19-27]. Also, more recently, the Schwinger effect
by an SU(2) gauge field during inflation for scalar particles and fermions was
calculated in [28] and [29,30].
On the other hand, one of the most serious questions in the standard cosmology is
whether the universe has a beginning or has existed eternally, and this question has
been leading us into a profound discussion by using general relativity and modern
cosmology. The standard cosmological model implies that the universe stems from a
Big Bang singularity. To elude this singularity, Ellis et al.
[31,32] proposed an interesting model, called Emergent Universe (EU), in
which the universe originates from an Einstein static state rather than a Big Bang
singularity, and therefore, there is no time-like singularity.
In this paper, we study the mechanism of particle creation in a spatially closed
Robertson-Walker model with the scale factor a(t)=a0+AeH0t, where α 0, A and H
0 are positive constants [33-35]. In this universe, there is no time-like
singularity. It asymptotically coincides with the Einstein static model in the
infinite past α(t) → α 0 and, it approaches to a de
Sitter expansion phase at late times a(t) →AeH0t. In the beginning, we consider a spin-0 scalar in spatially closed
Robertson-Walker spacetime in the context of the emergent universe scenario. Then we
solve the Klein-Gordon equation by introducing two successive changes of variables.
In order to study the mechanism of particle creation, we use the canonical method
based on Bogoliubov transformation connecting the “in” and “out” coefficients. This
method allows us to find the number density of the created particles and the total
energy.
2. The Klein-Gordon equation
To study the process of pair creation, we consider the case of spatially closed
Robertson-Walker universe with the metric,
ds2=dt2-a2(t)[dχ2+sin2χdθ2+sin2θdφ2],
(2)
Where 0⩽χ⩽π,,0≤θ<π,0<φ<2π. The wave equation for a real massive scalar field which is coupled to
the closed Robertson-Walker background, takes the form
1-g∂μ(gμν-g∂νψ)+(m2+ζR)ψ=0,
(3)
where R = g
µν
R
µν
is the Ricci scalar and ζ is a numerical factor which takes
the value ζ = 0 in the minimal coupling case and,
ζ = 1/6 when a conformal coupling is
considered. In this case, the equation of a massive scalar field is written as
(∂2∂t2+3a˙a∂∂t-1a2t[∂2∂χ2+2cotχ∂∂χ-1sin2χ×∂2∂θ2+cotθ∂∂θ+1sin2θ∂2∂φ2]+m2)ψ=0,
(4)
where we have neglected the numerical factor ζ to yield minimal
coupling (i.e. ζ = 0). To solve the differential
equation (4), we write the solution ψ (t,χ,θ,φ) in
the form
ψ(t,χ,θ,φ)=a-32(t)Yn,l,μ(χ,θ,φ)Ψ(t),
(5)
Where Yn,l,μ are the scalar harmonics on three-sphere S
3 and, n⩾l⩾0 and l⩾μ⩾-l. These harmonics can be expressed in terms of the standard
S
2 scalar harmonics Yl,μ(θ,φ) as
Yn,l,μ(χ,θ,φ)=Hn,l(χ)Yl,μ(θ,φ).
(6)
The eigenfunctions Hn,l(χ) satisfy the following differential equation [36,37]
[∂2∂χ2+2cotχ∂∂χ-ll+1sin2χ]×Hn,l(χ)=-n(n+2)Hn,l(χ).
(7)
with
Hn,l(χ)=sinlχCn-ll+1(cos(χ)),
(8)
and Cn-ll+1(cos(χ)) are Gegenbauer polynomials [36,37].
The S
3 scalar harmonics Yn,l,μ satisfy the following orthonormality conditions:
∫Yn,l,μ(χ,θ,φ)Y*n',l',μ'(χ,θ,φ)sin2χdχ×sinθdθdφ=δnn'δll'δμμ'.
(9)
Substituting Eq. (5), (6) and (7) in Eq. (4), we obtain the differential equation for
Ψ(t),
[∂2∂t2+ωn2t]Ψ(t)=0,
(10)
where
ωn2(t)=m2-32AH02etH0a0+AeH0t-34(AH0etH0a0+AeH0t)2+n(n+2)(a0+AeH0t)2.
(11)
The Eq. (10) involves n and so, in general, the number of produced
particles will depend on n. Equation (10), on the other hand, does
not depend on the angular eingenvalues l, and so the number of produced particles are always independent of
l in closed Robertson-Walker spacetime. Note that Eq. (10) is similar to
that of the harmonic oscillator with a time-dependent frequency.
Let us analyze the behavior of the time equation when t → ±∞. In the
asymptotic past t → −∞, Eq. (10) reduces
to
[∂2∂t2+ωn,in]Ψ(t)=0;n(n+2)a02+m2=ωn,in,
(12)
with the solutions
Ψn,in≃e-iωn,int2ωn,in;Ψn,in*≃eiωn,int2ωn,in.
(13)
On the other hand, in the asymptotic future t → +∞,
Eq. (10) yields
[∂2∂t2+ωout]Ψ(t)=0; ωout=m2-9H024,
(14)
with the solutions
Ψout(t)≃e-iωoutt2ωout;Ψout*(t)≃eiωoutt2ωout.
(15)
We see that ω
out
does not depend on the label n. This result is not
surprising because in the future infinity we coincide with a de Sitter spacetime
[38]. By making two successive changes of
variables as
η=∫dta(t)
and ξ=eH0a0η, the Eq. (10) takes the form
((1-ξ)ξd2dξ2+(1-2ξ)ddξ+m2H02-94(1-ξ)+n(n+2)H02a02+m2H02ξ-n(n+2)a02H02-34)Ψ(ξ)=0.
(16)
The singularities of this differential equation are ξ =
0,1 and ∞, and all are regular singularities. We can recognize
this differential equation as a hypergeometric one by imposing the substitution,
Ψ(ξ)=(1-ξ)κξυΞ(ξ).
(17)
This, substituted into the differential equation, gives,
(d2dξ2+(1+2υ-2(υ+κ+1)ξ)ddξ-(υ+κ+12)2+n(n+2)a02H02-1)Ξ(ξ)=0,
(18)
where κ = (iω
out
/H
0) and υ = (iω
n,in
/H
0). The equation above is a hypergeometric equation whose solution around
the origin ξ = 0 is given in terms of the hypergeometric functions
as [39]
Ξ1=F(12+υ+κ+iϑn,12+υ+κ-iϑn,1+2υ;ξ),
(19)
Ξ2=ξ-2υF(12-υ+κ+iϑn,12-υ+κ-iϑn,1-2υ;ξ),
(20)
and the solution Ψ(ξ) of Eq. (16) finally reads,
Ψ1=ξυ(1-ξ)κF(12+υ+κ+iϑn,12+υ+κ-iϑn,1+2υ;ξ),
(21)
Ψ2=(1-ξ)κξ-υF(12-υ+κ+iϑn,12-υ+κ-iϑn,1-2υ;ξ),
(22)
where ϑn=(n(n+2)/a02H02)-1. Using the invariance of Eq. (16) under the transformation
ξ → 1 − ξ and ω
n,in
→ ω
out
, we find another set of solutions
Ψ3=(1-ξ)κξυF(12+υ+κ+iϑn,12+υ+κ-iϑn,1+2κ;1-ξ),
(23)
Ψ4=ξυ(1-ξ)-κF(12+υ-κ+iϑn,12-κ+υ-iϑn,1-2κ,1-ξ).
(24)
In the next section we will use the solutions of the field equation to analyze the
mechanism of particle creation.
3. Pair creation
In order to study the process of particle creation, we will discuss the asymptotic
behavior of the solutions of the Klein-Gordon equation when t → ±∞,
or equivalently when ξ → 0,1. Firstly, when
t → −∞ or ξ → 0, we have
limξ→0Ψ1=limξ→0(1-ξ)κξυ2ωnin×F(a,b,c;ξ)≃eiωn,int2ωn,in,
(25)
limξ→0Ψ2=limξ→0(1-ξ)κξ-υ2ωn,in×F(a',b',c';ξ)≃-eiωn,int2ωn,in,
(26)
where F (α,b,c;0) = 1. Then, as
t → −∞, the positive and negative frequency modes are
Ψn,in*=Ψ1; Ψn,in=Ψ2.
(27)
The modes (25), (26) may be used to define particle states and a Fock space in the
Heisenberg picture in the standard way. In particular, the field modes Ψ
n
may be expanded
Ψn=anΨn,in+an+Ψn,in*,
(28)
where the operators αn
,an+ obey the commutation relations
an,an'+=δnn',an,an'=an+,an'+=0.
(29)
Similarly, in the “out” region, when t → +∞ or ξ →
1, we have
limξ→0Ψn3=limξ→0(1-ξ)κξυ2ωout×F(a,b,c;1-ξ)≃e-iωoutt2ωout,
(30)
limξ→0Ψn4=limξ→0ξυ(1-ξ)-κ2ωout×F(a',b',c';1-ξ)≃eiωoutt2ωout,
(31)
and the positive and negative frequency modes as t → +∞ are
Ψn4=Ψn,out*; Ψn3=Ψn,out.
(32)
The field modes Ψ
n
can be expanded in terms of these “out” modes as,
Ψn=bnΨnout+bn+Ψn*out,
(33)
where
bn,bn'+=δnn',bn,bn'=[bn+,bn'+]=0.
(34)
There are two different vacua |0
in
⟩ and |0
out
⟩ associated with two Fock spaces Fin and Fout
{an|0in⟩=0, ∀ nbn|0out⟩=0, ∀ n
(35)
The creation and annhilation operators are related by the relations
{an=αnbn+βnbn+bn=αn*an-βn*an+,
(36)
where αn and
βn are the Bogolioubov’s
coefficients. In order to obtain the density of created particles, we use the so
called Bogoliubov transformation, connecting the “in” (at t → −∞)
with the “out” (at t → +∞ ) states,
Ψn,in=αnΨn,out+βnΨn,out*.
(37)
The “in” state is written in terms of the outgoing positive and negative solutions
and this is the origin of particle creation by a gravitational field. The
coefficients α
n
and β
n
are the Bogoliubov coefficients satisfying the bosonic relation given by
|αn|2-|βn|2=1.
(38)
By using the relation between the hypergeometric functions [39], namely,
F(a,b,c,ϰ)=Γ(c)Γ(c-a-b)Γ(c-b)Γ(c-a)×F(a,b,a+b-c+1,1-ϰ)+Γ(c)Γ(a+b-c)Γ(b)Γ(a)(1-ϰ)c-a-b×F(c-a,c-b,c-a-b+1,1-ϰ),
(39)
and
F(a,b,c,y)=(1-y)c-a-bF(c-a,c-b,c,y),
(40)
we find that the Bogoliubov coefficients are
αn=ωoutωn,inΓ(1-2iωn,inH0)Γ(-2iωoutH0)Γ(12-iωn,in+iωoutH0+iϑn)Γ(12-iωn,in-iωoutH0-iϑn),
(41)
βn=ωoutωn,inΓ(1-2iωn,inH0)Γ(2iωoutH0)Γ(12-iωn,in-ωoutH0-iϑn)Γ(12-iωn,in-ωoutH0+iϑn).
(42)
So, the number of particles is given by:
Nn=⟨0in|bn+bn|0in⟩=|βn|2.
(43)
A direct calculation gives
Nn=coshπ(ωn,in-ωoutH0-ϑn)coshπ(ωn,in-ωoutH0+ϑn)sinh2πωn,inH0sinh2πωoutH0,
(44)
where we used the relations,
|Γ(ix)|2=πxsinhπx; |Γ(1+ix)|2=πxsinhπx; |Γ(12+ix)|2=πcoshπx.
(45)
The total number of the produced particles is obtained by taking the sum over all the
oscillation modes as
N=∑n=0∞(n+1)2coshπ(ωn,in-ωoutH0-ϑn)coshπ(ωn,in-ωoutH0+ϑn)sinh2πωn,inH0sinh2πωoutH0,
(46)
and the total energy is given by
E=∑n=0∞ωout(n+1)2coshπ(ωn,in-ωoutH0-ϑn)coshπ(ωn,in-ωoutH0+ϑn)sinh2πωn,inH0sinh2πωoutH0,
(47)
where (n + 1)2 is the degree of degeneracy.
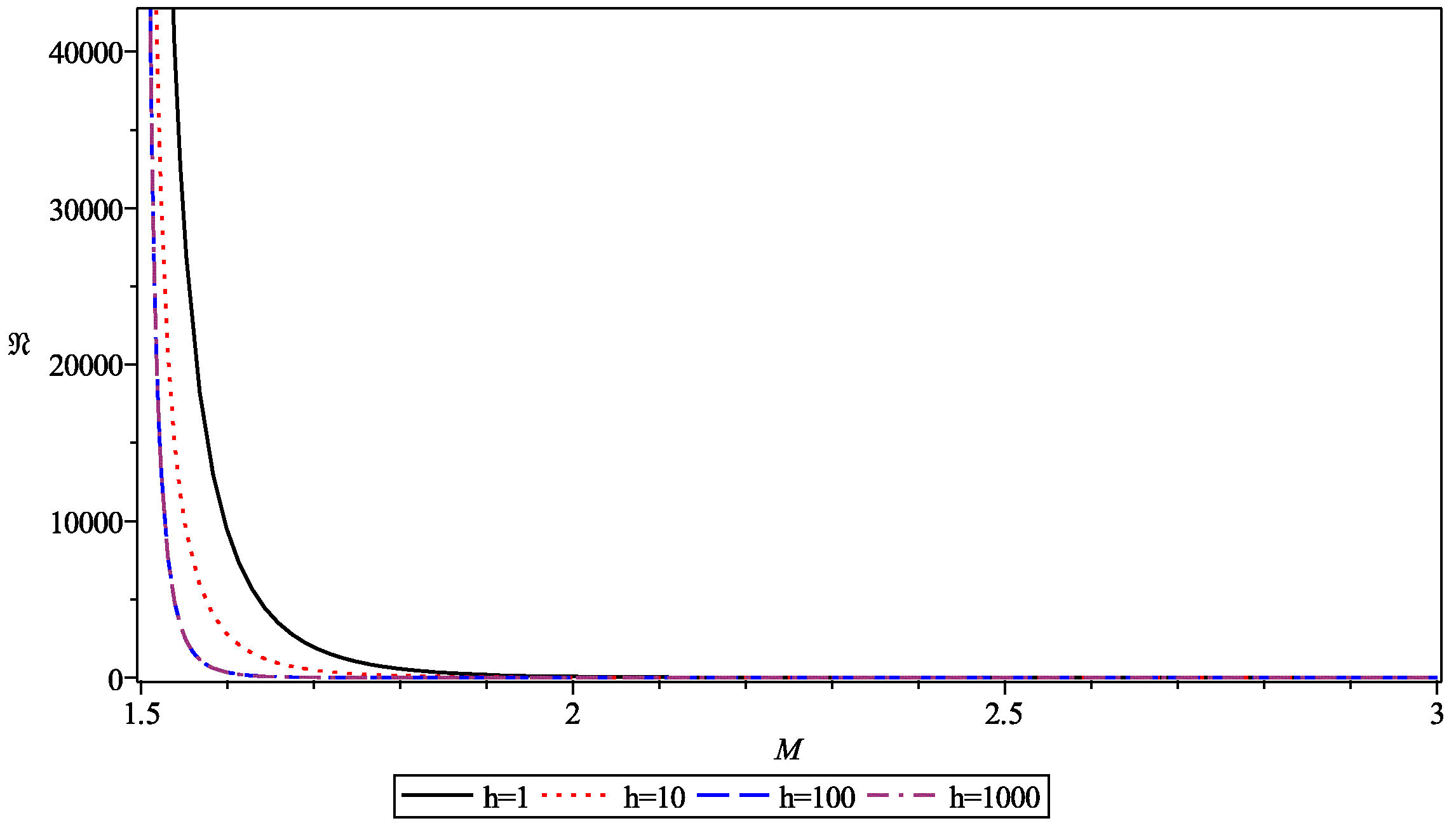
In Fig. 1, we plot the total number of produced
particles (N) as a function of variable M =
m/H0 for several values of h =
α0H0. The Eq. (46) has an infinite sum
over all oscillation modes. Thus, we need to truncate the infinite series in order
to perform a numerical study for the total number of particles. We calculated the
sum for 100, 1000 and 10000 terms and concluded that the number of particles
increases with the number of terms taken into the summation indicating a divergence,
while leaving the character of the curves unchanged. For 100, 1000 and 10000 terms,
we have the number of particles in the numerical order 104,
107∼8 and 1010∼11, respectively. In Fig. 1, we present the values obtained for the summation of 100
terms that shows the curves clearly. The number of produced particles decreases
rapidly with M. Changes in the parameter h change
the behavior of the curves very slightly. While small values of h
produce individual curves, the curves start to coincide as h
increases. We did not include the curve for h = 10000 for
simplicity as it also coincides with the curves associated with h =
100 and h = 1000.
Indeed, the sums in Eqs. (46) and (47) are quite divergent, therefore the “in” and
“out” representations are unitarily inequivalent, since Bogoliubov transformations
need not to be unitary. Otherwise, it is remarkable that the system evolves slowly
and continuously over time, which corresponds to the adiabatic regime. Consequently,
the study of the frequency ωn2(t) in equations (10) and (11) implies that the asymptotic behavior of
Ψ(t) when t → ±∞ is approximated by a WKB
solution. Therefore, in order to regularize this divergence to find a sensible
result, we consider that the process of pair production occurs at the time of
maximum violation of the adiabatic condition, namely (d/dt)log|(ω˙/ω2)|=0, around time t
c
and we can cut-off the sum at n = N
c
, which is the highest value of n [40-42].
Then the expressions of the total number N of particles and the total energy are written according to
N
c
as follows
N=∑n=0Nc(n+1)2coshπ(ωn,in-ωoutH0-ϑn)coshπ(ωn,in-ωoutH0+ϑn)sinh2πωn,inH0sinh2πωoutH0,
(48)
E=∑n=0Ncωout(n+1)2coshπ(ωn,in-ωoutH0-ϑn)coshπ(ωn,in-ωoutH0+ϑn)sinh2πωn,inH0sinh2πωoutH0,
(49)
and their asymptotic behaviours are given respectively by
N≃13Nc3sinh(2πωoutH0),
(50)
and
E≃13Nc3ωoutsinh(2πωoutH0).
(51)
Finally, let us study the limit α 0 → 0 that reproduces the de Sitter
case. By taking into account that
n(n+2)→k2, H0→H and lima0→0ωn,in=|k|a0, lima0→0ϑn=|k|Ha0,
(52)
where k2=kx2+ky2+kn2. For these conditions, Eq. (44) becomes
Na0→0=lima0→0coshπ(m2H-94)coshπ(2|k|Ha0-m2H-94)sinh(2π|k|Ha0)sinh(2πm2H-94).
(53)
By using of the formula
limz→+∞sinhz→ez; limz→+∞coshz→ez,
(54)
we obtain
Na0→0=[e2πm2H-94-1]-1,
(55)
and this result agrees exactly with that of [43]. Integrating this expression over all wave modes gives a divergent
result,
1(2π)3∫d3kNa0→0=Na0→0(2π)2∫0+∞k2dk.
(56)
We introduce k
c
as the highest value of the momentum for which the pairs have been created at
a given time [40-42]. Consequently, the total number of created particles is
given by
1(2π)3∫d3kNa0→0=kc3Na0→06π2.
(57)
4. Conclusion
We studied an explicit calculation of the Klein-Gordon equation in spatially closed
Robertson-Walker universe with the emergent universe (EU) scenarios whose scale
factor evolution is modeled by a(t)=a0+AeH0t. It is remarkable that this universe is characterized by the absence of
the time-like singularity and, it asymptotically coincides with the Einstein static
model in the infinite past and it approaches to a de Sitter expansion phase at late
times.
The exact solution of the Klein-Gordon equation is obtained in terms of the
hypergeometric functions for the temporal part, multiplied by the scalar harmonics
on three-sphere S
3. To calculate the total number of produced particles and the total
energy associated with them, we analyzed the asymptotic behavior of the solutions of
the Klein-Gordon equation when t → ±∞ in order to determine the
suitable choice of the “in” and “out” states. Consequently, we applied the usual
method of Bogoliubov transformations to find the coefficients connecting the “in”
and “out” states that directly yield our results. We plotted the number of produced
particles using a truncated series as a function of m/H
0 to see that the number of produced particles decreases rapidly with
m/H
0. Finally, we studied the limit α 0 → 0 that reproduced the
de Sitter case as expected.
References
1. F. Sauter, Über das Verhalten eines Elektrons im homogenen
elektrischen Feld nach der relativistischen Theorie Diracs, Z.
Phys. 69 (1931) 742,
https://doi.org/10.1007/BF01339461.
[ Links ]
2. W. Heisenberg and H. Euler,
arXiv:physics/0605038.
[ Links ]
3. J. Schwinger, On Gauge Invariance and Vacuum Polarization,
Phys. Rev. 82 (1951) 664,
https://doi.org/10.1103/PhysRev.82.664.
[ Links ]
4. S. P. Gavrilov and D. M. Gitman, Vacuum instability in external
fields, Phys. Rev. D 53 (1996) 7162,
https://doi.org/10.1103/PhysRevD.53.7162.
[ Links ]
5. A. I. Nikishov, Barrier scattering in field theory removal of
Klein paradox, Nucl. Phys. B 21 (1970) 346,
https://doi.org/10.1016/0550-3213(70)90527-4.
[ Links ]
6. L. Parker, Particle Creation in Expanding Universes,
Phys. Rev. Lett. 21 (1968) 562,
https://doi.org/10.1103/PhysRevLett.21.562.
[ Links ]
7. L. Parker, Quantized Fields and Particle Creation in Expanding
Universes. I, Phys. Rev. 183 (1969) 1057,
https://doi.org/10.1103/PhysRev.183.1057.
[ Links ]
8. L. Parker, Quantized Fields and Particle Creation in Expanding
Universes. II, Phys. Rev. D 3 (1971) 346,
https://doi.org/10.1103/PhysRevD.3.346.
[ Links ]
9. E. Mottola, Particle creation in de Sitter space, Phys.
Rev. D 31 (1985) 754,
https://doi.org/10.1103/PhysRevD.31.754.
[ Links ]
10. A. A. Grib, S. G. Mamayev, and V. M. Mostepanenko, Particle
creation from vacuum in homogeneous isotropic models of the Universe,
Gen. Relat. Gravit. 7 (1976) 535,
https://doi.org/10.1007/BF00766413.
[ Links ]
11. A. A. Grib, S. G. Mamayev, and V. M. Mostepanenko, Vacuum
quantum effects in strong fields (Friedmann Laboratory Pub., St. Petersburg,
1994).
[ Links ]
12. D. M. Chitre and J. B. Hartle, Path-integral quantization and
cosmological particle production: An example, Phys. Rev. D 16
(1977) 251, https://doi.org/10.1103/PhysRevD.16.251.
[ Links ]
13. J. B. Hartle and S. W. Hawking, Path-integral derivation of
black-hole radiance, Phys. Rev. D 13 (1976) 2188,
https://doi.org/10.1103/PhysRevD.13.2188.
[ Links ]
14. S. P. Gavrilov, D. M. Gitman, and S. D. Odintsov, Quantum Scalar
Field in the FRW Universe with a Constant Electromagnetic Background,
Int. J. Mod. Phys. A 12 (1997) 4837,
https://doi.org/10.1142/S0217751X97002589.
[ Links ]
15. S. Biswas, J. Guha, and N. G. Sarkar, Particle production in de
Sitter space, Class. Quantum Grav. 12 (1995) 1591,
https://doi.org/10.1088/0264-9381/12/7/005.
[ Links ]
16. S. Biswas, A. Shaw, and B. Modak, Schoringer result on particle
production from complex paths WKB approximation, Int. J. Mod. Phys.
A 15 (2000) 3717,
https://doi.org/10.1142/S0217751X00001221.
[ Links ]
17. V. M. Villalba and W. Greiner, Creation of scalar and Dirac
particles in the presence of a time varying electric field in an anisotropic
Bianchi type I universe, Phys. Rev. D 65 (2001) 025007,
https://doi.org/10.1103/PhysRevD.65. 025007.
[ Links ]
18. V. M. Villalba, Creation of scalar particles in the presence of
a constant electric field in an anisotropic cosmological universe, Phys.
Rev. D 60 (1999) 127501,
https://doi.org/10.1103/PhysRevD.60.127501.
[ Links ]
19. E. Bavarsad, S. P. Kim, C. Stahl, and S.-S. Xue, Effect of a
magnetic field on Schwinger mechanism in de Sitter spacetime, Phys. Rev.
D 97 (2018) 025017,
https://doi.org/10.1103/PhysRevD.97.025017.
[ Links ]
20. T. Kobayashi and N. Afshordi, Schwinger effect in 4D de Sitter
space and constraints on magnetogenesis in the early universe, J. High
Energy Phys. 2014 (2014) 166,
https://doi.org/10.1007/JHEP10(2014)166.
[ Links ]
21. C. Stahl and S.-S. Xue, Schwinger effect and backreaction in de
Sitter spacetime, Phys. Lett. B 760 (2016) 288,
https://doi.org/10.1016/j.physletb.2016.07.011.
[ Links ]
22. M. B. Fröb et al., , Schwinger effect in de
Sitter space, J. Cosmol. Astropart. Phys. 2014 (2014) 009,
https://doi.org/10.1088/1475-7516/2014/04/009.
[ Links ]
23. T. Hayashinaka, T. Fujita, and J. Yokoyama, Fermionic Schwinger
effect and induced current in de Sitter space, J. Cosmol. Astropart.
Phys. 2016 (2016) 010,
https://doi.org/10.1088/1475-7516/2016/07/010.
[ Links ]
24. S. P. Gavrilov, D. M. Gitman, and A. A. Shishmarev, Pair
production from the vacuum by a weakly inhomogeneous space-dependent electric
potential, Phys. Rev. D 99 (2019) 116014,
https://doi.org/10.1103/PhysRevD.99.116014.
[ Links ]
25. S. P. Gavrilov, D. M. Gitman, and A. A. Shishmarev, Particle
scattering and vacuum instability by exponential steps, Phys. Rev.
D 96 (2017) 096020,
https://doi.org/10.1103/PhysRevD.96.096020.
[ Links ]
26. B. Hamil and M. Merad, Schwinger mechanism on de Sitter
background, Int. J. Mod. Phys. A 33 (2018) 1850177,
https://doi.org/10.1142/S0217751X18501774.
[ Links ]
27. B. Hamil, Pair creation of neutral Dirac particle in (1+2)d
noncommutative spacetime, Mod. Phys. Lett. A 33 (2018) 1850017,
https://doi.org/10.1142/S0217732318500177.
[ Links ]
28. K. D. Lozanov, A. Maleknejad, and E. Komatsu, Schwinger effect
by an SU(2) gauge field during inflation, J. High
Energy Phys. 2019 (2019) 41,
https://doi.org/10.1007/JHEP02(2019)041.
[ Links ]
29. L. Mirzagholi, A. Maleknejad, and K. D. Lozanov, Production and
backreaction of fermions from axion-SU(2) gauge fields during
inflation, Phys. Rev. D 101 (2020) 083528,
https://doi.org/10.1103/PhysRevD.101.083528.
[ Links ]
30. V. Domcke, Y. Ema, K. Mukaida, and R. Sato, Chiral anomaly and
Schwinger effect in non-abelian gauge theories, J. High Energy
Phys. 2019 (2019) 111,
https://doi.org/10.1007/JHEP03(2019)111.
[ Links ]
31. G. F. R. Ellis, J. Murugan, and C. G. Tsagas, The emergent
universe: an explicit construction, Class. Quantum Gravit. 21
(2003) 233, https://doi.org/10.1088/0264-9381/21/1/016.
[ Links ]
32. G. F. R. Ellis and R. Maartens, The emergent universe:
inflationary cosmology with no singularity, Class. Quantum
Gravit. 21 (2003) 223,
https://doi.org/10.1088/0264-9381/21/1/015.
[ Links ]
33. P. Labraña, Emergent universe scenario and the low CMB
multipoles, Phys. Rev. D 91 (2015) 083534,
https://doi.org/10.1103/PhysRevD.91.083534.
[ Links ]
34. C. Ríos, P. Labraña, and A. Cid, The Emergent Universe and the
Anomalies in the Cosmic Microwave Background, J. Phys.: Conf.
Ser. 720 (2016) 012008,
https://doi.org/10.1088/1742-6596/720/1/012008.
[ Links ]
35. P. Labrana, Emergent Universe Scenario and the Low CMB˜
Multipoles, J. Phys.: Conf. Ser. 720 (2016) 012016,
https://doi.org/10.1088/1742-6596/720/1/012016.
[ Links ]
36. L. Lindblom, N. W. Taylor, and F. Zhang, Scalar, vector and
tensor harmonics on the three-sphere, Gen. Relativ. Gravit. 49
(2017) 139, https://doi.org/10.1007/s10714-017-2303-y.
[ Links ]
37. V. D. Sandberg, Tensor spherical harmonics on S2 and
S3 as eigenvalue problems, J. Math. Phys. 19
(1978) 2441, https://doi.org/10.1063/1.523649.
[ Links ]
38. J. Garriga, Pair production by an electric field in (1 +
1)dimensional de Sitter space, Phys. Rev. D 49 (1994) 6343,
https://doi.org/10.1103/PhysRevD.49.6343.
[ Links ]
39. I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals,
Series, and Products, 4th ed. (Academic Press, New York,
1980).
[ Links ]
40. T. Kobayashia and N. Afshordi, JHEP10, 166
(2014).
[ Links ]
41. M. B. Fröb et al., , Schwinger effect in de
Sitter space, J. Cosmol. Astropart. Phys. 2014 (2014) 009,
https://doi.org/10.1088/1475-7516/2014/04/009.
[ Links ]
42. M. Banyeres, G. Domènech, and J. Garriga, Vacuum birefringence
and the Schwinger effect in (3+1) de Sitter, J. Cosmol. Astropart.
Phys. 2018 (2018) 023,
https://doi.org/10.1088/1475-7516/2018/10/023.
[ Links ]
43. T. Markkanen and A. Rajantie, Massive scalar field evolution in
de Sitter, J. High Energy Phys. 2017 (2017) 133,
https://doi.org/10.1007/JHEP01(2017)133.
[ Links ]











 nueva página del texto (beta)
nueva página del texto (beta)