1. Introduction
In spite of the fact that Standard Model (SM) works almost perfectly, it fails to explain the neutrino experimental data, dark matter, baryon asymmetry of the universe and so forth1. Speaking about the mixings, the lepton sector exhibits a peculiar pattern which is totally different to the quark sector where the mixing matrix is almost diagonal and this puzzle remains unsolved.
In this line of thought, hierarchical quark mass matrices as the nearest neighbor interaction (NNI) textures2-5 and those that possess the generalized Fritzsch textures6, fit quite well the CKM matrix. In the lepton sector, according to the experimental data, the PMNS matrix has large values in its entries which can be explained by the presence of a symmetry behind the neutrino mass matrix. Currently, we can find in the literature elegant proposals (and their respective breaking) as the µ ↔ τ symmetry7 (see reference therein), µ ↔ τ reflection symmetry8-13, Tri-Bimaximal14-19, Cobimaximal mixing matrices20-25. Moreover, hierarchical mass matrices as the Fritzsch26 and the generalized Fritzsch textures6 also accommodate the PMNS mixing matrix.
The flavor symmetries27-30 have been useful to obtain textures in the fermion mass matrices and the corresponding mixing patterns. For example, the S3 discrete group has been studied in great detail in different scenarios31-48. In the mentioned literature there are few models49,50 where the Fritzsch textures have been implemented. Hence, the main purpose that we pursuit is to realize those textures by means the S3 flavor symmetry however we obtain a modified Fritzsch textures which are different to previous studies in the sense that there is an extra parameter in the lepton mass matrices. As a result of that, the theoretical mixing angles formulas come out distinct but their predictions are in accordance with experimental data.
Due to the last neutrino oscillations data seem to favor the normal hierarchy51, in this paper, we construct a non-renormalizable lepton model in the type II see-saw scenario where the S3⊗Z2 flavor symmetry controls the masses and mixings. We stress that the scalar sector of the mentioned model keeps intact so that flavons are included to generate the mixings. The effective neutrino as well as the charged lepton mass matrices are hierarchical and these have (under a benchmark in the charged sector) a kind of Fritzsch textures that accommodate the mixing angles in good agreement with the last experimental data. The model predicts consistent values for the CP-violating phase and the |mee| effective Majorana neutrino mass rate. Along with this, the branching ratio for the lepton flavor violation process, µ → eγ, is below the current bound.
The paper is organized as follows. The theoretical framework and matter content of the model are reviewed in section II, the flavored model is also described; we construct, in the section III, the PMNS mixing matrix and relevant features are pointed out. An analytical study is performed on the mixing angles expressions to find out the parameter space that fits the observables, this together with a numerical analysis in section IV. In section V, we give some model predictions and some interesting conclusions are shown in section VI.
2. The framework
We make a scalar extension of the SM that is based on the gauge group SU(3)C⊗SU(2)L⊗U(1)Y, however we will focus in the lepton sector so that the matter content is given by
In the scalar sector, we have
where the Higgs triplet provides mass to the active neutrinos by means of the type II see-saw mechanism. In addition, three flavons, 𝜙(1,2,3), which are singlets under the gauge group, will generate the lepton mixings.
In this appealing framework, the Lagrangian can be read as
where the most general scalar potential, which is gauge invariant, is given by
We ought to remark that the flavor invariant scalar potential is not written explicitly because we are only interested in studying the masses and mixings. Nonetheless, let us address a brief comment for the flavons sector, according to the assignation given in Table I, the flavored invariant scalar potential can be mimicked by that one with three Higgs doublets as we can see in Refs.33,39,48. In here, we will just assume a vacuum expectation value (vev) alignment of the flavons, 〈𝜙〉I = v𝜙(1,0) and 〈𝜙3〉 = v𝜙3, that provide the mixings and this also reduce the free parameters in the lepton mass matrices. We emphasize that the mentioned vev’s alignment was obtained in a model with S3 symmetry and four Higgs doublets49; two of them (the other two) belong to a doublet (singlets) of S3, in fact the scalar potential for three and four Higgs doublets shares similar structures and features. Then, we would expect to obtain the same pattern for flavons if a detailed study of the scalar potential was made but this will leave out.
Table I Assignation under the S3⊗Z2. Here, I = 1, 2.
| Matter | LI | L3 | eIR | e3R | 𝜙 I | 𝜙3 | ∆ | H |
|---|---|---|---|---|---|---|---|---|
| S3 | 2 | 1S | 2 | 1S | 2 | 1S | 1S | 1S |
| Z2 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 |
Let us speak briefly on the flavor symmetry. As is well known, the S327 has three dimensional real representation that can be decomposed as 3S = 2⊕1S or 3 A = 2⊕1 A (the reader might see the Appendix A for details). This is key for getting hierarchical mass matrices. In addition, the Z 2 discrete symmetry can be used to forbid some Yukawa couplings.
2.1 The model
As we already commented, in the present model, the scalar sector contains one Higgs doublet (H) and one triplet (Δ) so that some flavons will be added to the matter content in order to generate the mass textures that provide the mixings. The full assignation, under the S3⊗Z2 for the matter fields, is given in Table I.
As one can notice, due to the Z2 symmetry there are no-renormalizable Yukawa mass term, then, at the next leading order in the cutoff scale we havei
as a consequence the lepton mass matrices have the following structure
with
Since that neutrino mass matrix, that comes from the type II see-saw mechanism, is symmetric
then
3. PMNS MIXING MATRIX
Due to the alignment, the mass matrices read as
As one can notice, if ae (av) was zero, the charged lepton (neutrino) mass matrix would possess implicitly the NNI (Fritzschiii) textures. In general, the charged lepton mass matrix has five complex free parameters that can be reduced a little bit more by adopting the benchmark ce ≈ fe. As a result, the lepton mass matrices have the Fritzsch textures but the entry a(v,e) will modify slightly those textures, as we will show next.
The mixing matrices that take place in the PMNS matrix are obtained as follows. Me and Mv are diagonalized respectively by Ue(L,R) and Uv such that
where ℓ = v, e.
We can observe that m ℓ can be written as
Notice that the second mass matrix has the Fritzsch texture but the there is a shift due to the aℓ parameter. Consequently, we expect a deviation to the Fritzsch prediction on the mixings. To see this, let us diagonalize the mass matrix, mℓ, where the CP violating phases are factorized as
The above matrix,
The CP violating phase can be absorbed in the lepton fields by choosing properly the following matrices u 𝑒𝐿 = P 𝑒 O 𝑒 , u 𝑒𝑅 = P 𝑒 † O 𝑒 and u 𝜈 = P 𝜈 O 𝜈 . Here, O ℓ is an orthogonal matrix that diagonalizes to
3.0.1. Normal Hierarchy (NH)
For this case, the diagonalization procedure is valid for charged lepton and the active neutrinos (ℓ = e, v). Then considering
where mℓ2 = -|mℓ2| in order to obtain real parameters. In addition, those must satisfy the constraint mℓ3 > |mℓ2| > mℓ1 > |aℓ| > 0. Having fixed some matrix elements, the eigenvectors of
Here, Nℓ and mℓi are normalization factors and the physical masses, respectively. Along with this, the normalization factors Nℓ can be fixed by the condition
After a lengthy task, we obtain
with
where
3.0.2. Inverted Hierarchy (IH)
We want to remind you that this ordering is only valid for neutrinos, this means ℓ = v so that
in this case, we choose m1 = -|m1| for getting real parameters. On the other hand, the eigenvectors have the same form as in Eq. (14) however the orthogonal matrix Ov is a little bit different due to the fact m1 = -|m1| so that Ov = (-X1, X2, X3). Therefore, the orthogonal real matrix is given by
where
with
Hence, the PMNS mixing matrix is given by
Finally, the reactor, atmospheric and solar angles might be obtained by means the following expressions
Let us remark that |ae|, |av| and ηv are free parameters to be constrained. Along with this, the lightest neutrino mass is also a free parameter. As a result of this, we end up having four unknown parameters.
Before closing this section, a brief comment on the Majorana phases will be added. We have considered the CP parities for the complex neutrino masses which means that these can be either 0 or (. Thus, for the normal and inverted ordering we have (m3, m2, m1) = (+, -, +) and (m3, m2, m1) = (+, +, -,), respectively. Those CP parities values ensure that the fixed parameters given in Eq. (13) and Eq.(17) are reals.
4. Results
4.1. Analytical study
The purpose of this analytical study is to find out the free parameter values that fit the mixing angles. To do so, two neutrino masses can be fixed in terms of the squared mass scales
In addition, the experimental data, that will be used in this analytical and numerical study, is given in the Table II
| Observable | Experimental value |
|---|---|
| me(MeV) | 0.5109989461 ± 0.0000000031 |
| mµ(MeV) | 105.6583745 ± 0.0000024 |
| mτ(MeV) | 1776.86 ± 0.12 |
| Δm212/1 0-5 eV2 | 0.02200+0.069-0.062 |
| Δm312/1 0-5 eV2 | 2.55+0.02-0.03(2.45+0.02-0.03) |
| sin2 Θ12 | 0.318 ± 0.16 |
| sin2 Θ23 | 0.574 ± 0.14 (0.578+0.10-0.17) |
| sin2 Θ13 | 0.02200+0.069-0.062 (0.02225+0.064 -0.070) |
| δCP/° | 194+24-22 (284+26-28) |
In the current analysis, central values will be used for the normalized masses and there is a hierarchy among those, this is,
NH
where the particular 𝑚 1 ≈0.001 has been taken for this case.
IH
with m3 ( 0.01. This value is consistent with the current mass ordering.
Notice that particular values for the lightest neutrino mass have been considered for the normal and inverted hierarchy. Thus, we will obtain approximately the matrices Oe and Ov for the normal and inverted ordering, then the mixing angles must be calculated in analytical way for different scenarios.
NH
Case I:
Case II:
IH
Case I:
Case II:
Having obtained the above approximated matrices, let us obtain the mixing angles for two scenarios (both for the normal hierarchy) that seem to accommodate the observables.
Scenario A: If Oe and Ov were like Eq. (24), then the mixing angles would be
where the notable hierarchy in the charged lepton has been taken into account. In the above expressions, the reactor, atmospheric and solar angles are controlled by the ratio
Scenario B: If Oe and Ov were like Eqs. (24) and (25) respectively, then the mixing angles would be
As one can notice, the reactor angle is tiny in comparison to the scenario A, the atmospheric and solar angle are handled by the
To finish this section, let us add that one would expect changes in the mentioned scenarios when the lightest neutrino mass varies in its allowed region. Therefore, the numerical study will help us to discard one scenario.
4.2. Numerical study
To do the numerical analysis, we will be working with the following expressions
where mj with j = 1,3 represents the lightest neutrino mass for normal and inverted hierarchy, respectively.
Notice that the mixing angle expressions depend on the unknown parameters so that we will vary them in such a way that those satisfy their respective constraints. Taking into account the lightest neutrino mass, in the normal (inverted) ordering, we have
At the end of the day, we will obtain scattered plots for each observable as function of each unknown parameter. Subsequently, the Dirac (CP CP-violating phase and the effective Majorana neutrino mass are fitted and these are model predictions.
In the Fig. 1, we observe that there is a region (0.01 - 0.014 eV) for the lightest neutrino mass where the observables are in great according to the experimental results.
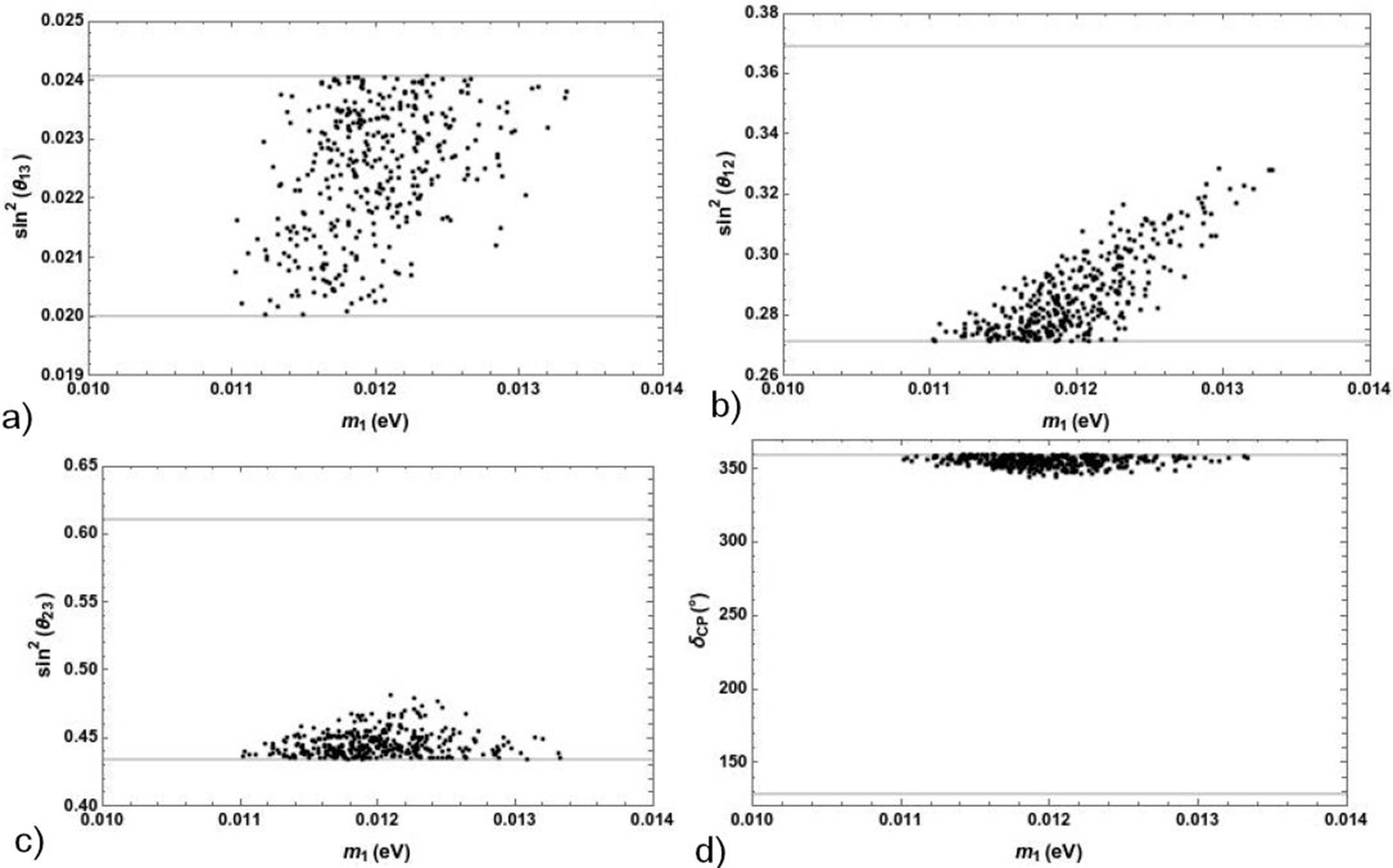
Figure 1 The reactor, solar, atmospheric angles and the Dirac CP phase as function of the lightest neutrino mass. The thick line stands for 3σ of C. L.
According to the Fig. 2, the av (ãv) prefers small values for fitting the mixing angles. This means the Fritzsch textures are favored but a small deviation is necessary to accommodate the observables up to 3σ.
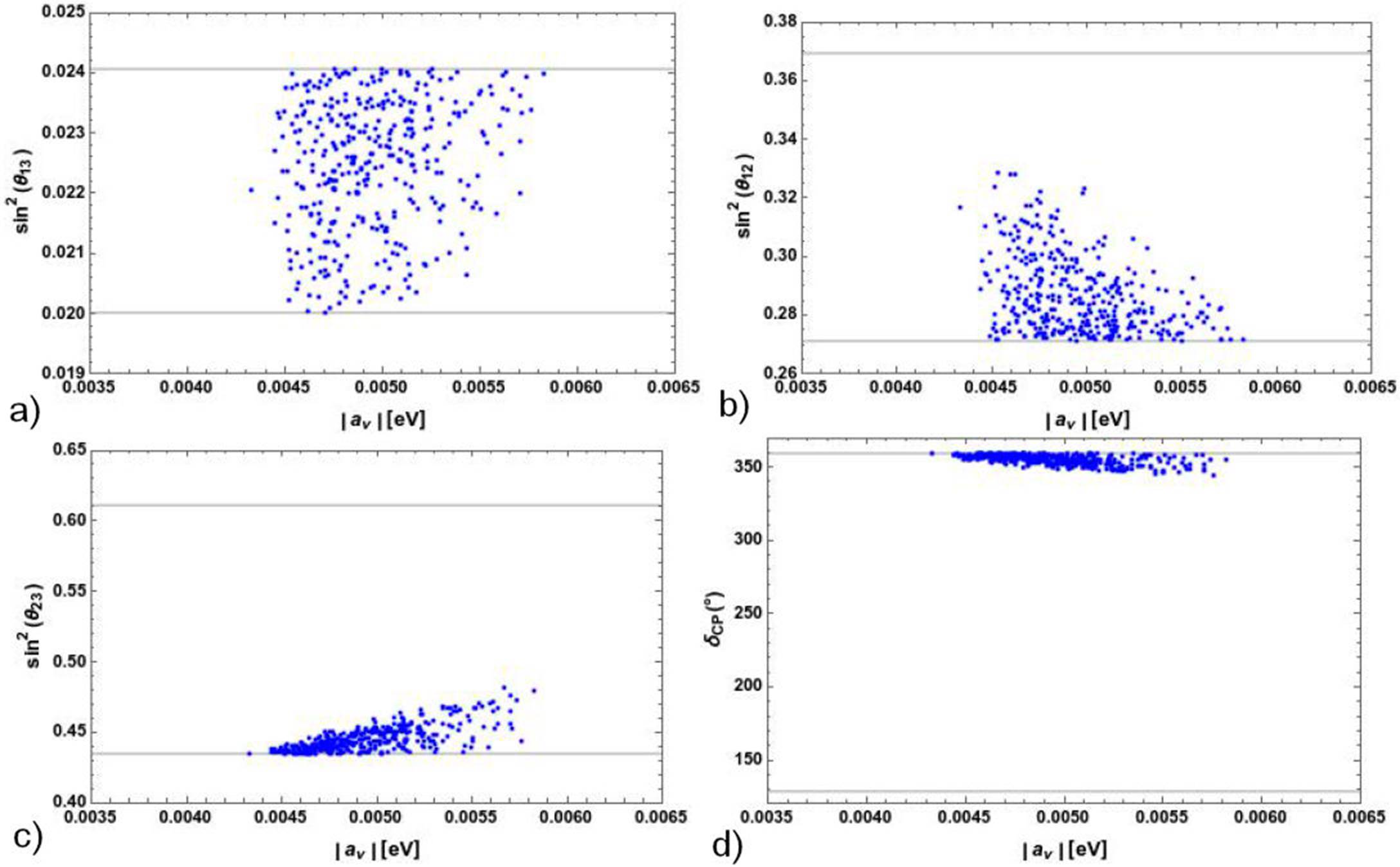
Figure 2 The reactor, solar, atmospheric angles and the Dirac CP phase as function of the |av| parameter. The thick line stands for 3σ of C. L.
In the charged lepton sector, the ae (ãe) parameter region is close to the electron mass as can be seen in Fig. 3, this is, ae ≈ me, so that the observables are well accommodated in the scenario C. Let us focus in the ηv phase which lies in a region around π value, the full region is shown in the Fig. 4.
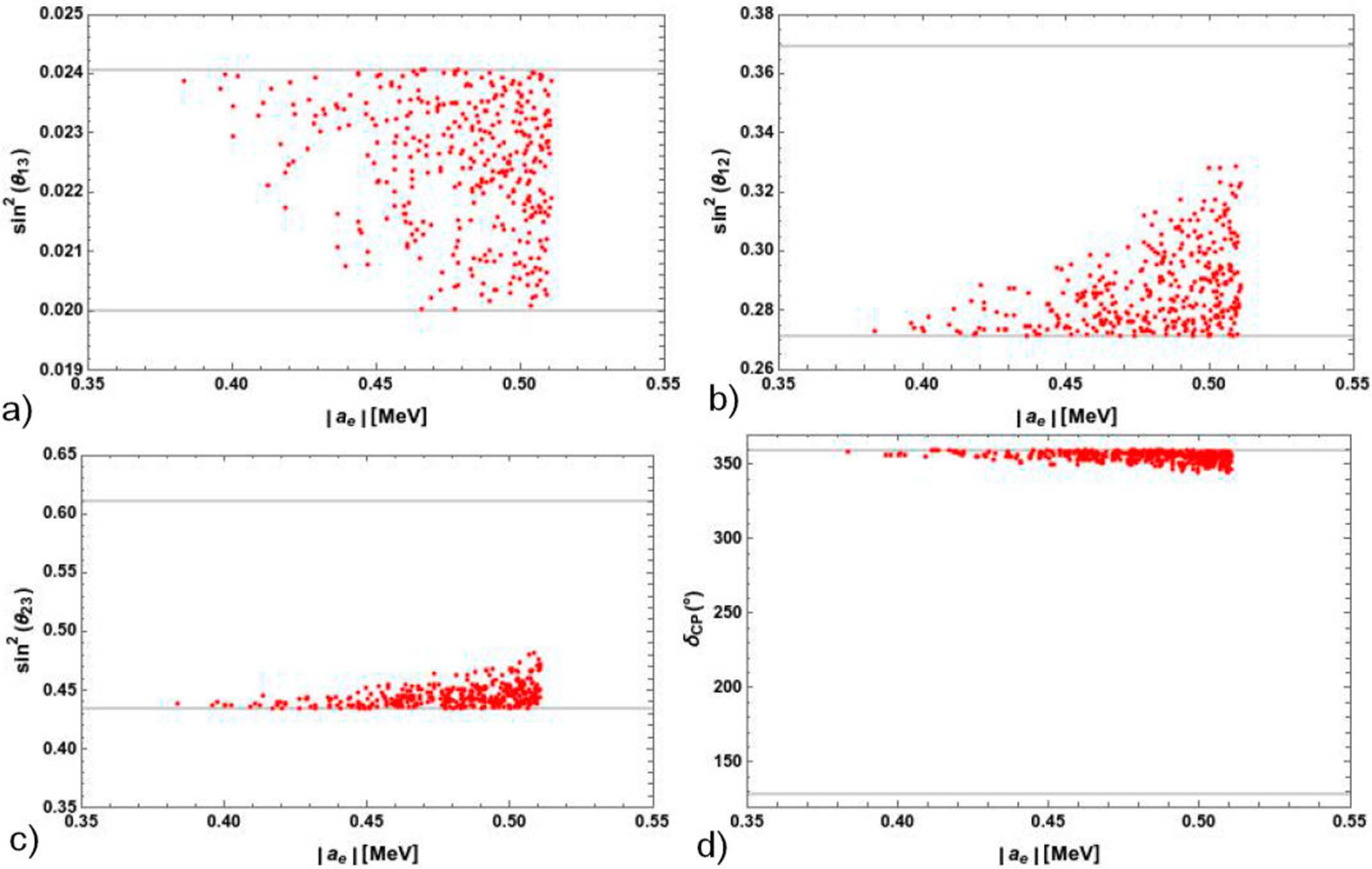
Figure 3 The reactor, solar, atmospheric angles and the Dirac CP phase as function of the |be| parameter. The thick line stands for 3σ of C. L.
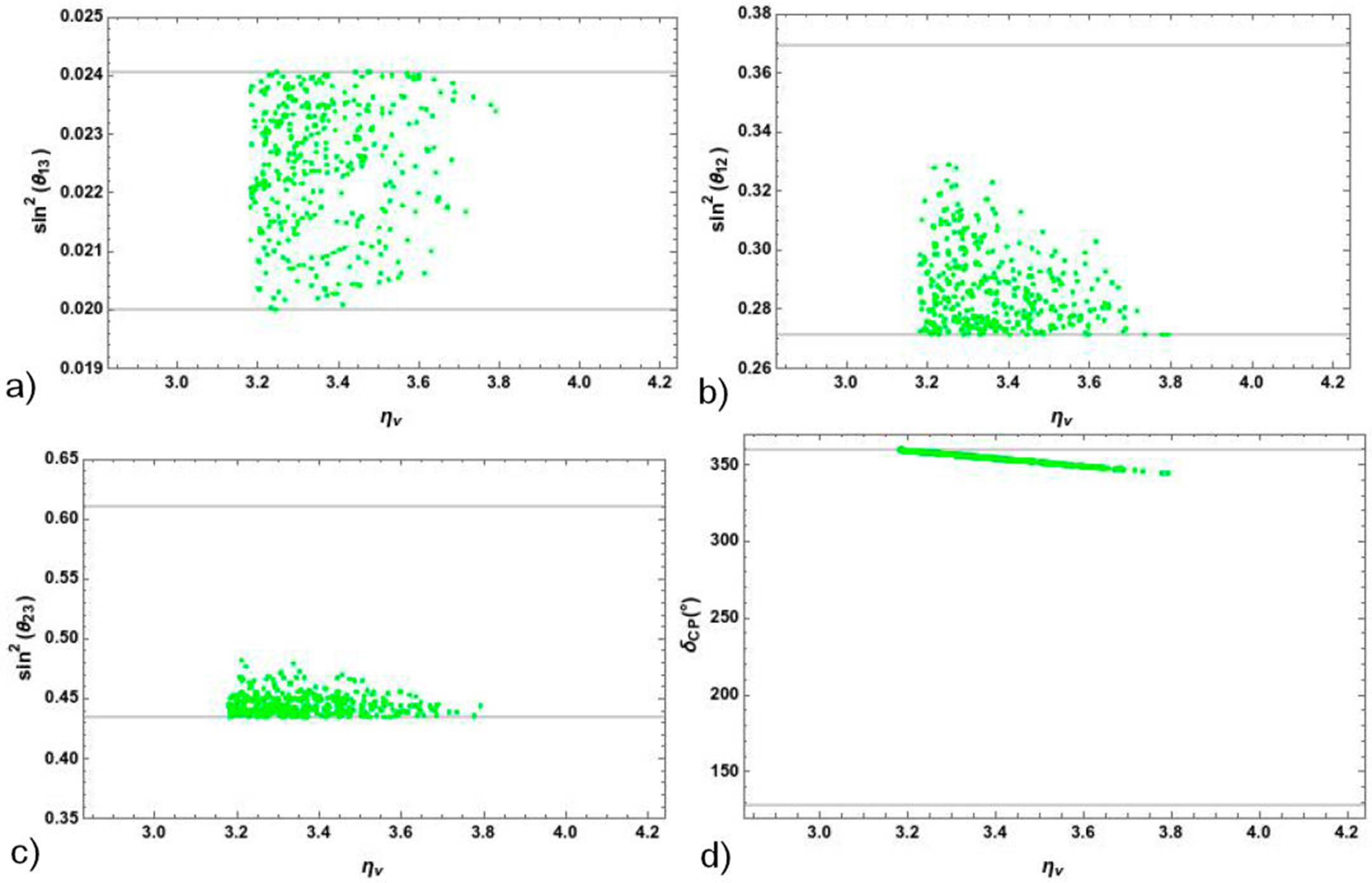
Figure 4 The reactor, solar, atmospheric angles and the Dirac CP phase as function of the effective phase, ηv, parameter. The thick line stands for 3σ of C. L.
To summarize, a set of free parameters has been found in which the reactor, solar and the atmospheric angles can accommodate quite well but this latter lies in the allowed low region (3σ). In addition, the model predicts large values for the Dirac CP-violating phase which is close to the up region according to the experimental data.
5. Model Predictions
5.1. Effective Majorana neutrino mass rate
Going back to the comment about CP parities for the complex neutrino masses, we want to perform the effective Majorana mass of the electron neutrino, which is defined by
where mi and Vei (i = 1, 2, 3) are the complex neutrino masses and PMNS matrix elements. As it is well known, the lowest upper bound on |mee| < 0.22 eV was provided by GERDA phase-I data53 and this value has been significantly reduced by GERDA phase-II data54.
In the previous section, we found a set of values for the free parameters (see Figs. 1 to 4 which fit the mixing angles. As a result, those values were used to find the regions for the effective Majorana mass of the electron neutrino, as shown in the Fig. 5.
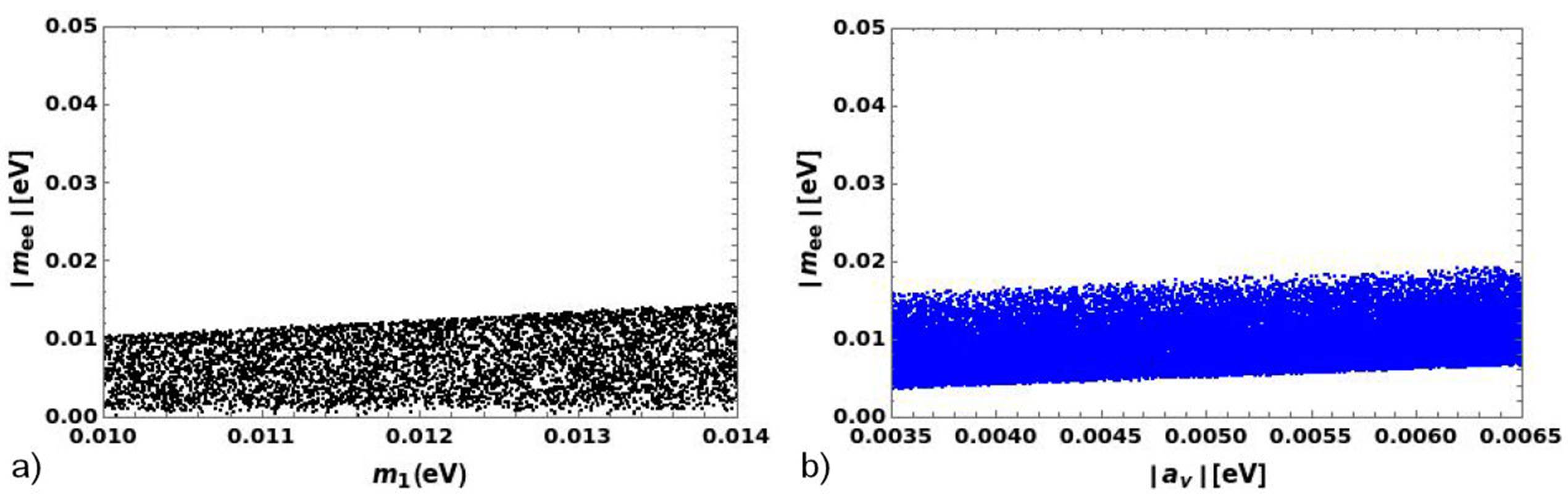
Figure 5 |mee| as function of m1 and |av|. These scattered plots correspond to the normal ordering where the CP parities for the complex neutrino masses are (m3, m2, m1) = (+, -, +).
For this observable, two scattered plots have been only shown since that parameters m1 and av are more restrictive for the allowed region.
5.2. Lepton violation process: µ → eγ
As an immediate result, the branching ratio for the lepton flavor violation process µ → eγ55,56 may be performed. As is well known, the doubly (Δ++) and singly (Δ+) charged scalars, that come from the Higgs triplet (see Eq. (2)), mediate this process. The theoretical formula for the branching ratio55 can be written as
where we have assumed that the scalar masses, mΔ+ = mΔ++ ( mΔ, are degenerated. In here, V represents the PMNS mixing matrix.
In the previous section, we constrained the free parameters that fit the mixing angles, in good approximation, we obtained the following regions: 0.01 < m1 < 0.014 eV, 0.35 MeV > |ae| < me, 0.004 < |av| < 0.006 eV and π < ηv < 6π/5. Having done that, the branching ratio for the lepton flavor violation process µ → eγ can be calculated by using the values 80 GeV < mΔ and vΔ < 5 GeV for the single and doubly charged scalar masses and the vev of the Higgs triplet, respectively.
The allowed region for the branching ratio, as function of the vev of the Higgs triplet and the mass of the singly and doubly charged scalars, is exhibited in the Fig. 6. As one can realize, the model predicts a region that is too much below of the experimental bound BR(µ → eγ) ≈ 4.2 ( 10-13.
6. Conclusions
We have built an economical non-renormalizable lepton model for getting the mixings where the type II see-saw mechanism is responsible to explain tiny neutrino masses. Under a particular benchmark, in the charged lepton sector, the mass matrices have the Fritzsch textures with a shift parameter which makes different to the previous studies. Our main finding is: a set of values for the relevant parameters was found to be consistent (up to 3σ) with the last experimental data on lepton observables for the normal neutrino mass ordering.
To finish, we would like to add that the S3⊗Z2 symmetry is an excellent candidate to be the flavor symmetry at low energy. However, one has to look for the best framework where the flavor symmetry solve the majority of open questions on the flavor problem and related issues. In this direction, the quark mixings and the scalar potential analysis will be included to have a complete study but this is a working progress.











 nueva página del texto (beta)
nueva página del texto (beta)



